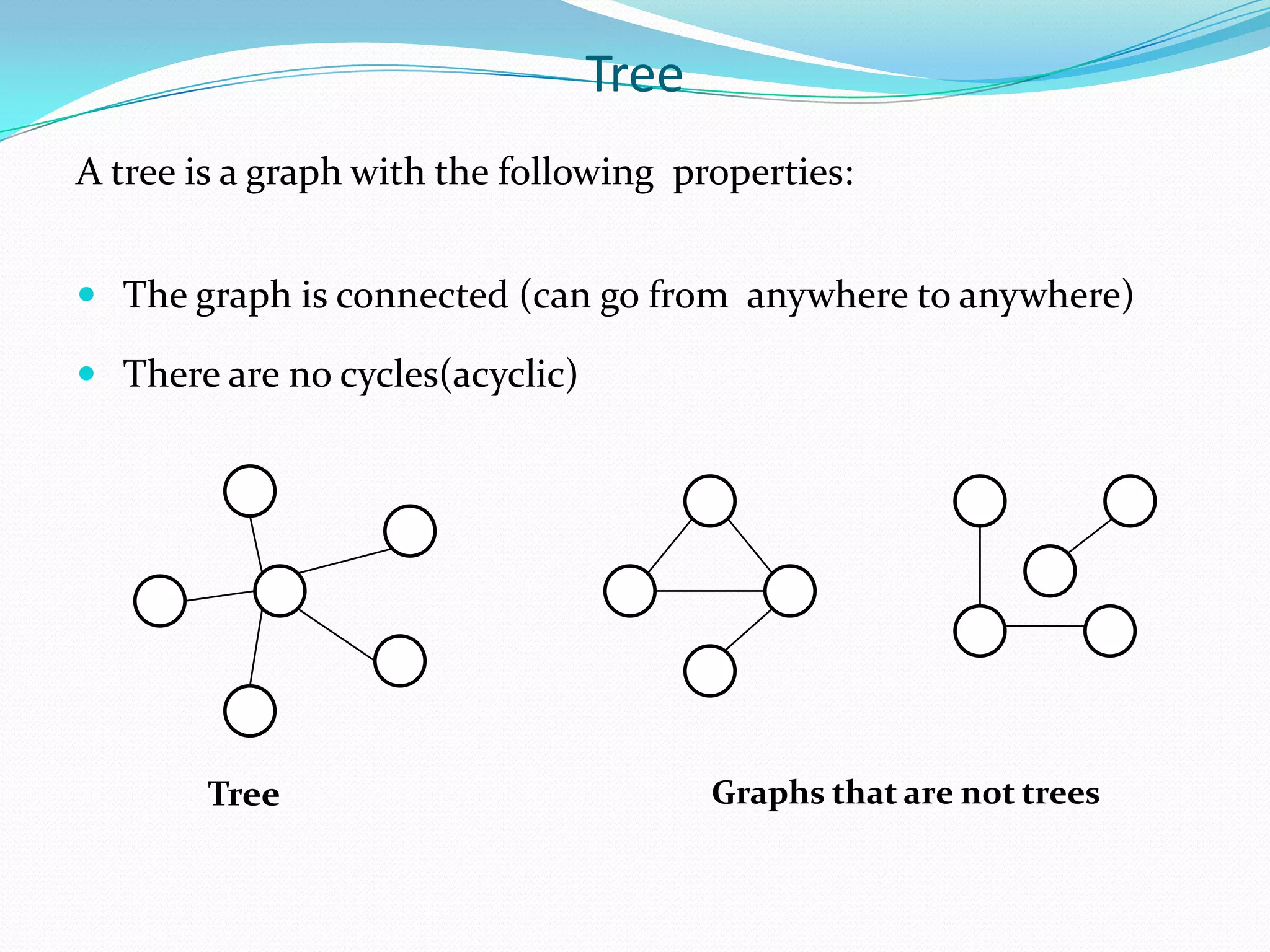
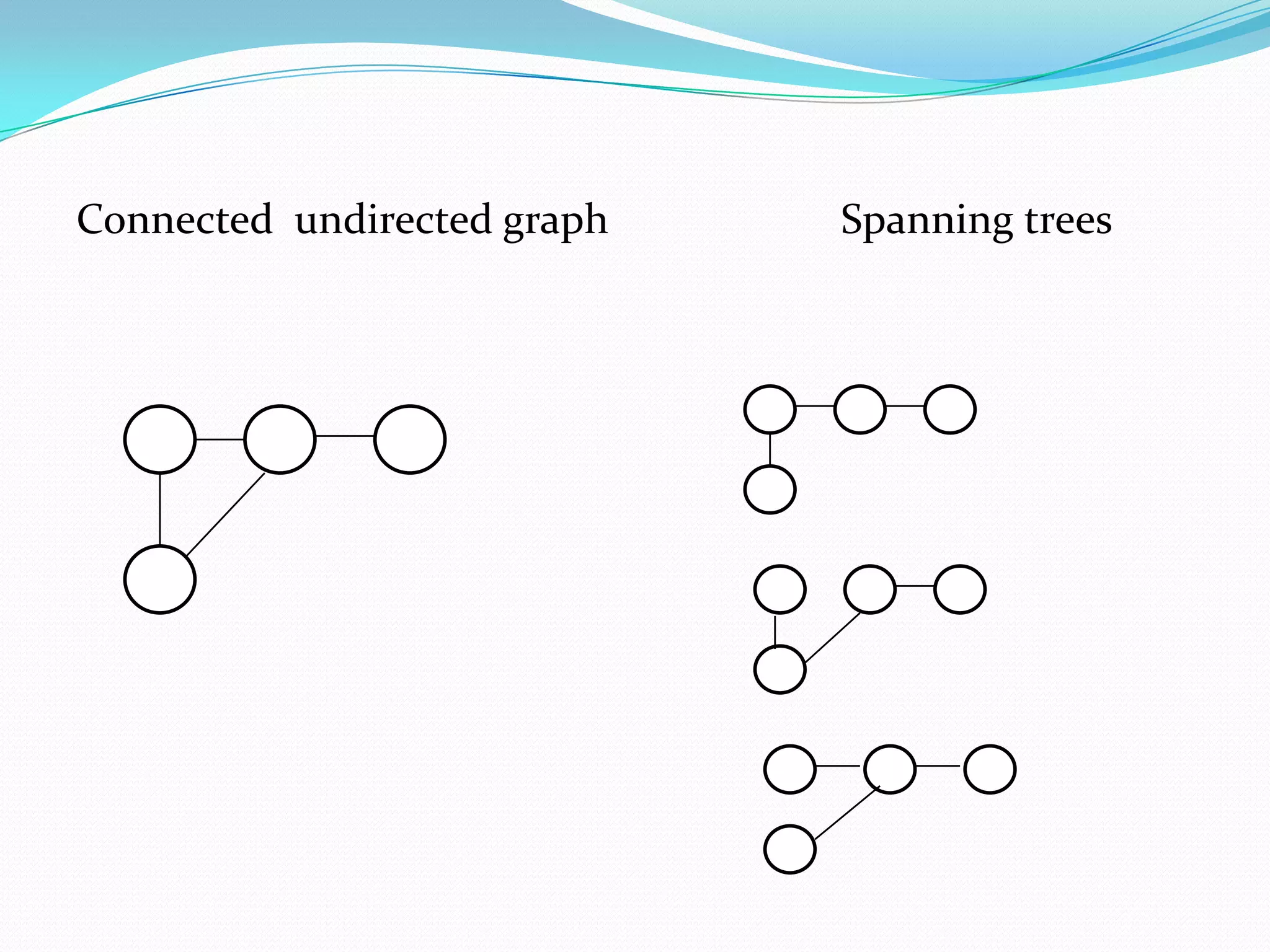
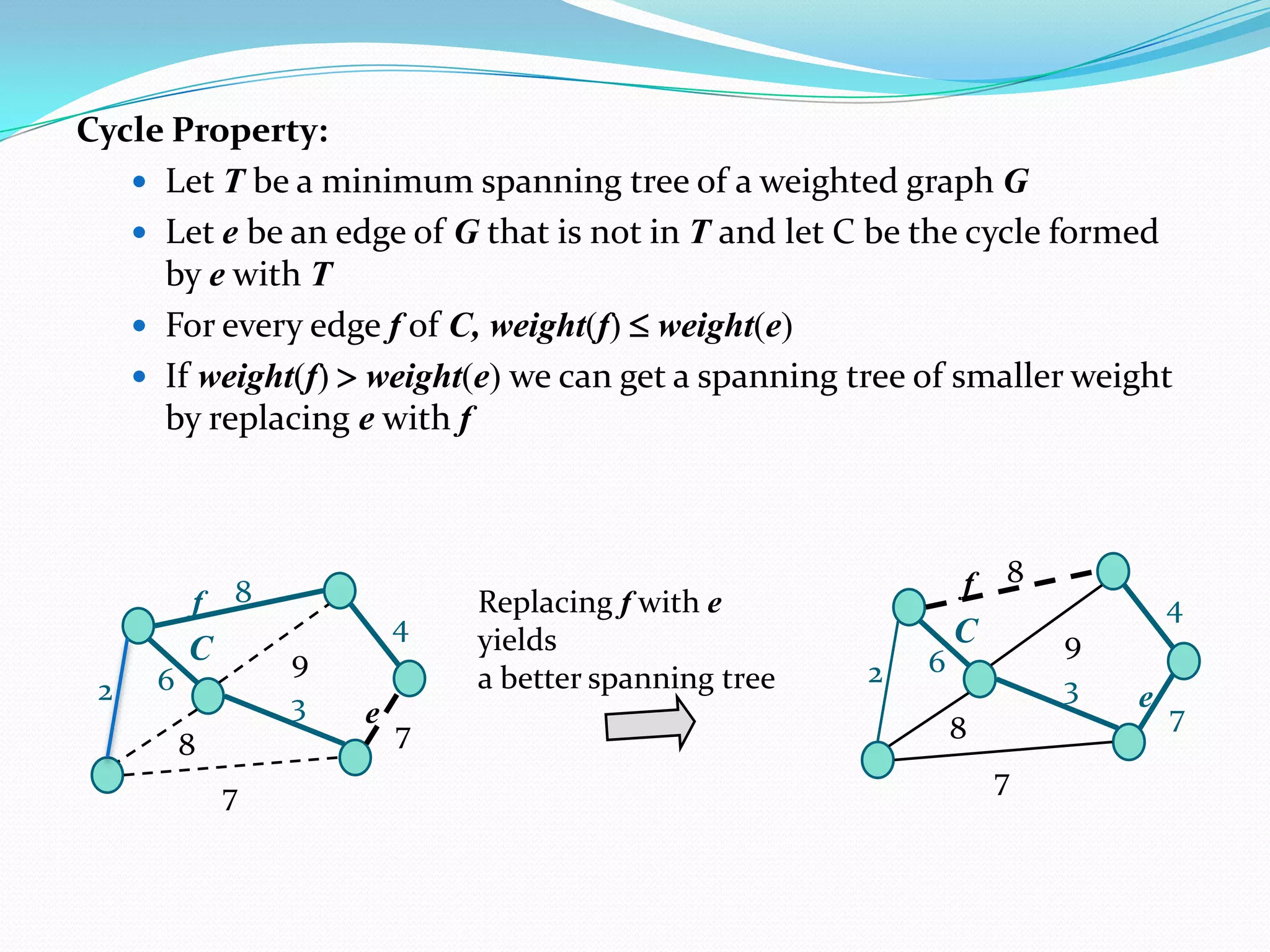
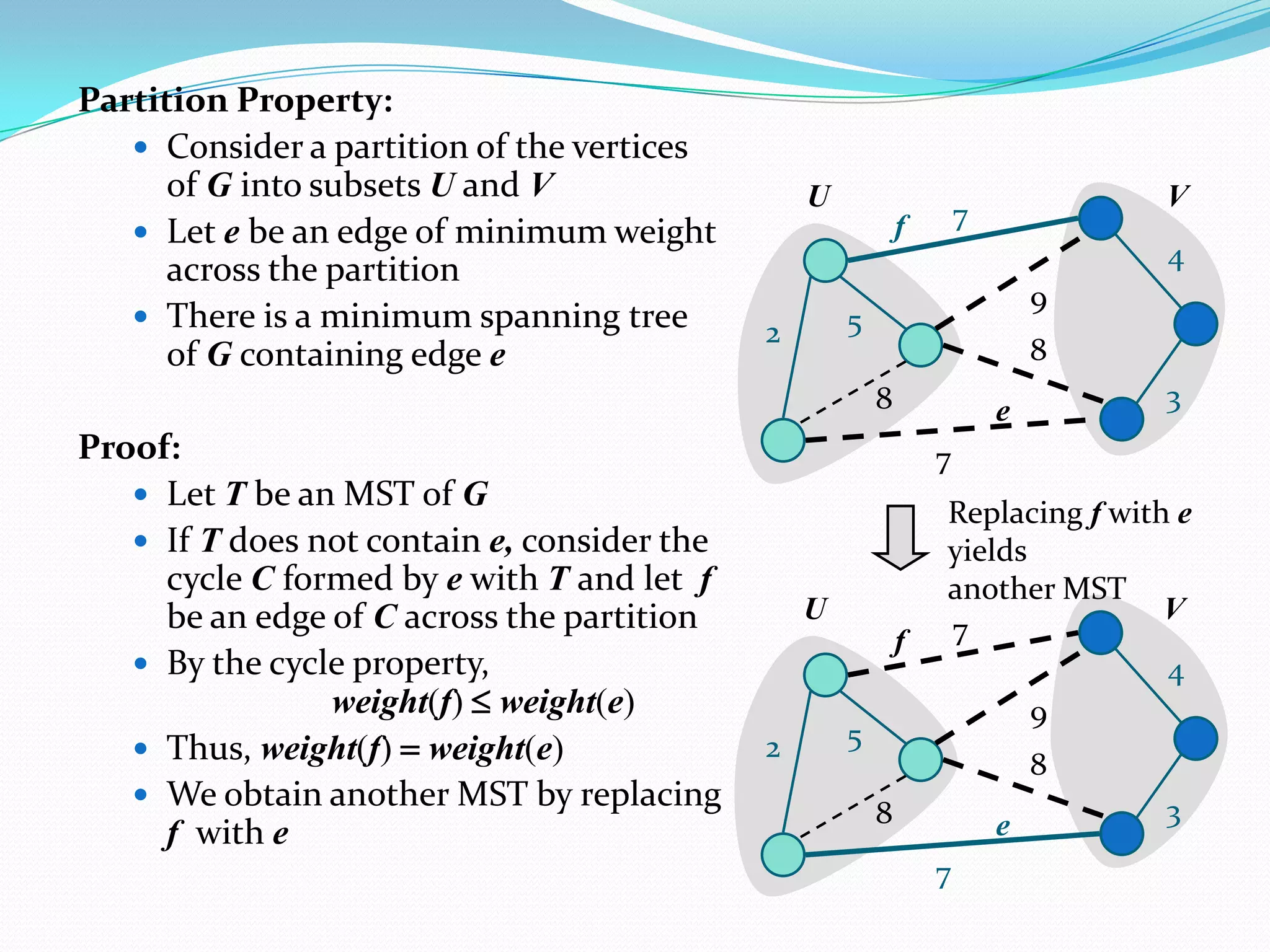
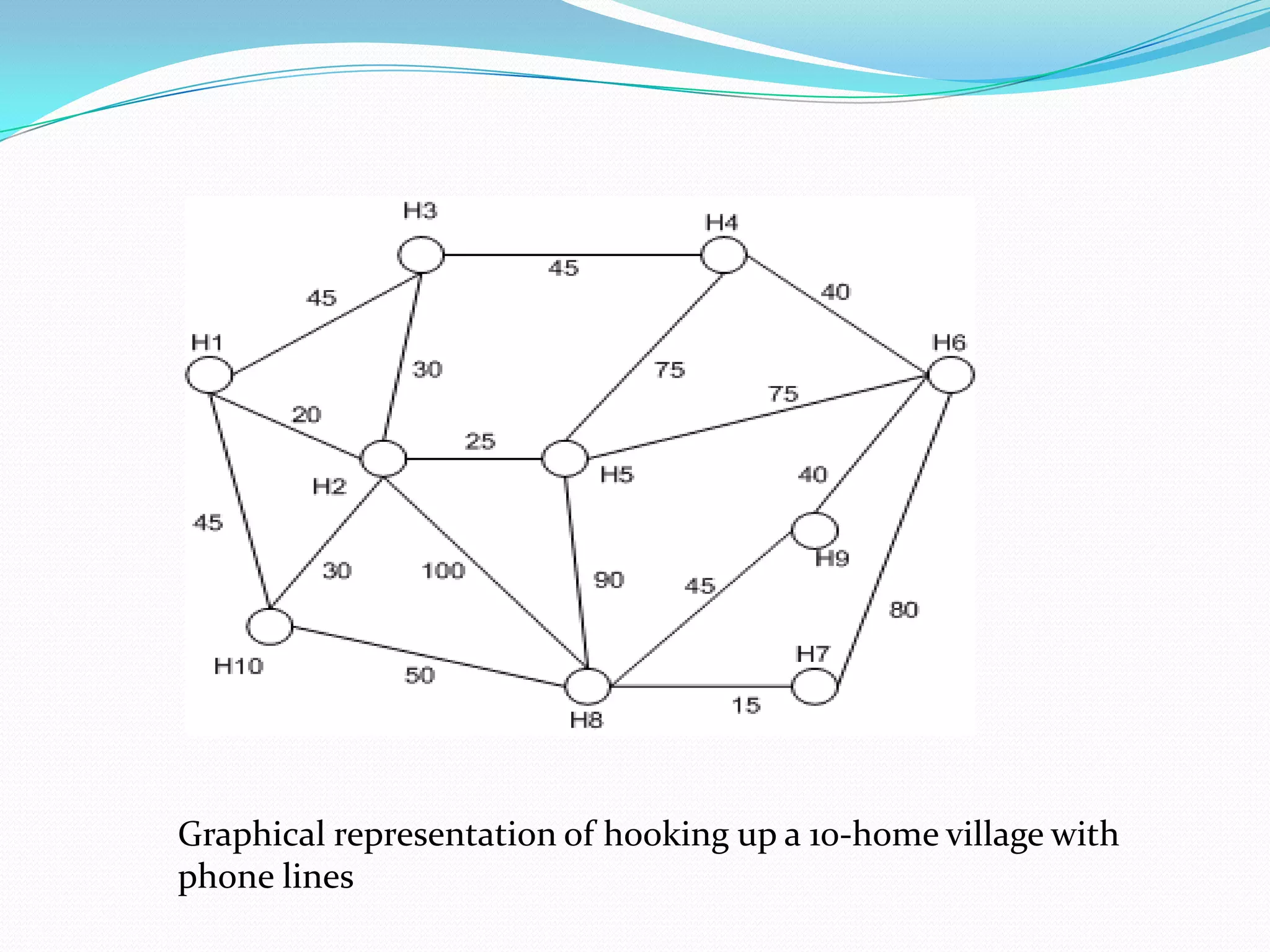
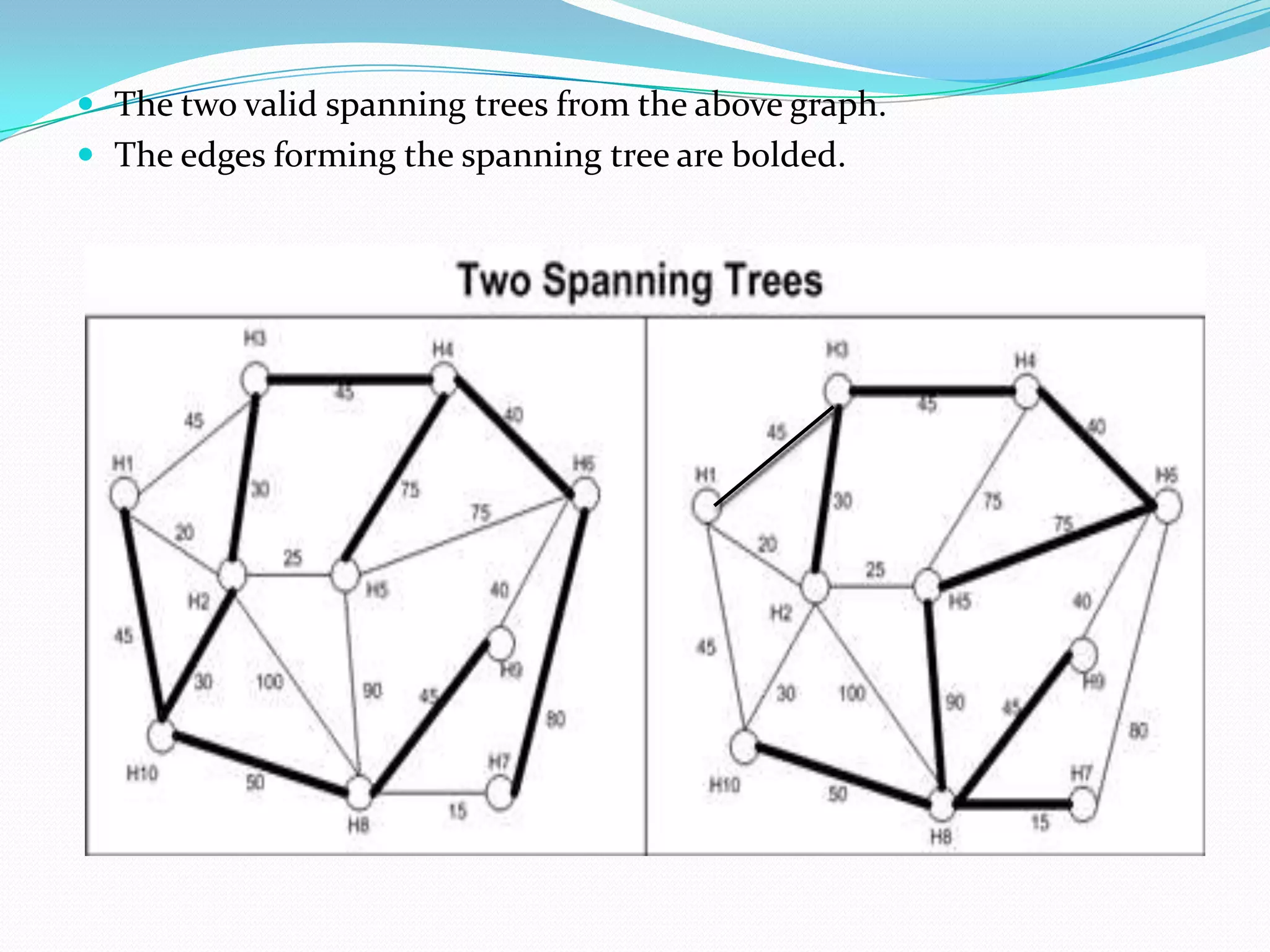
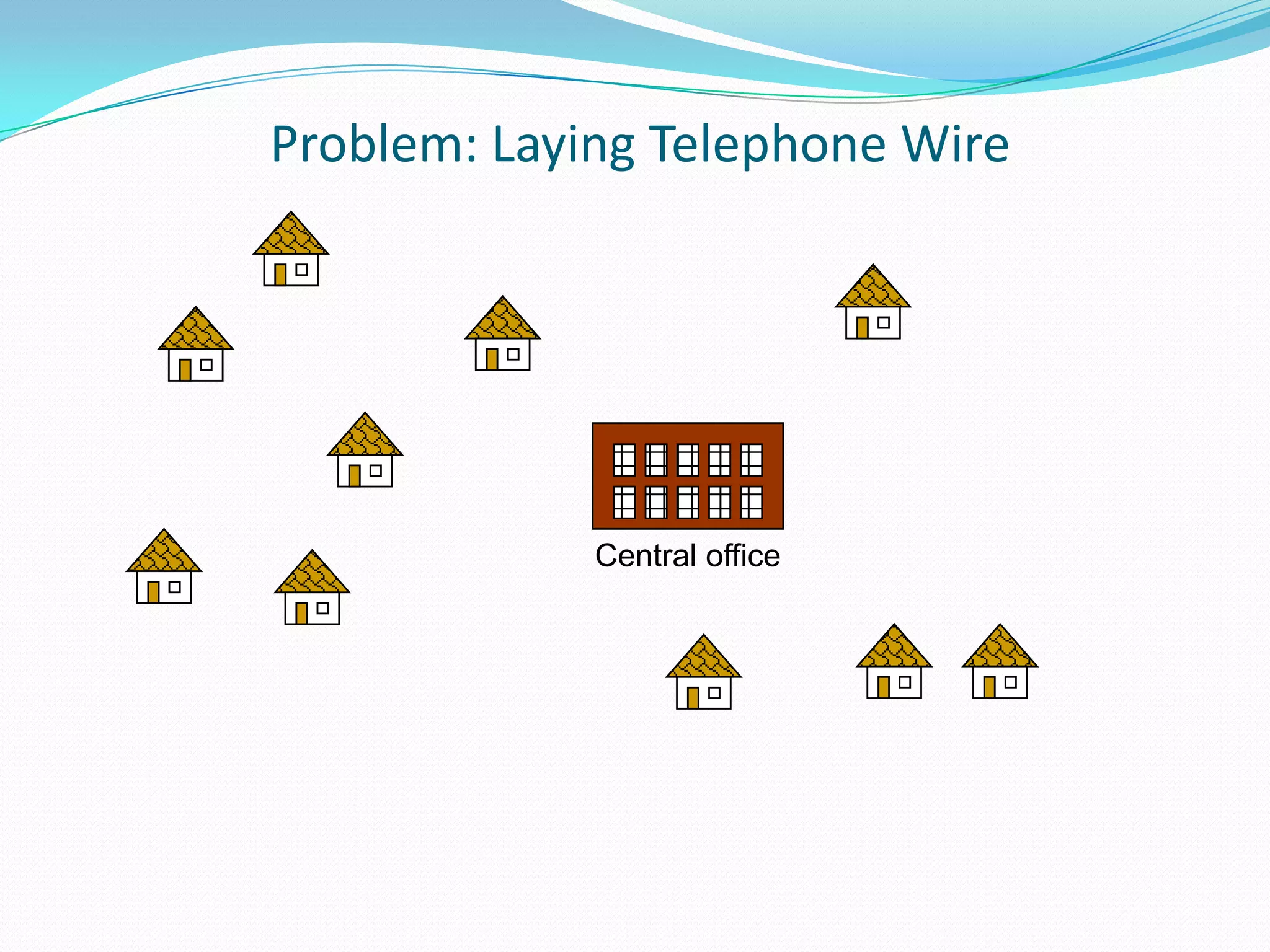
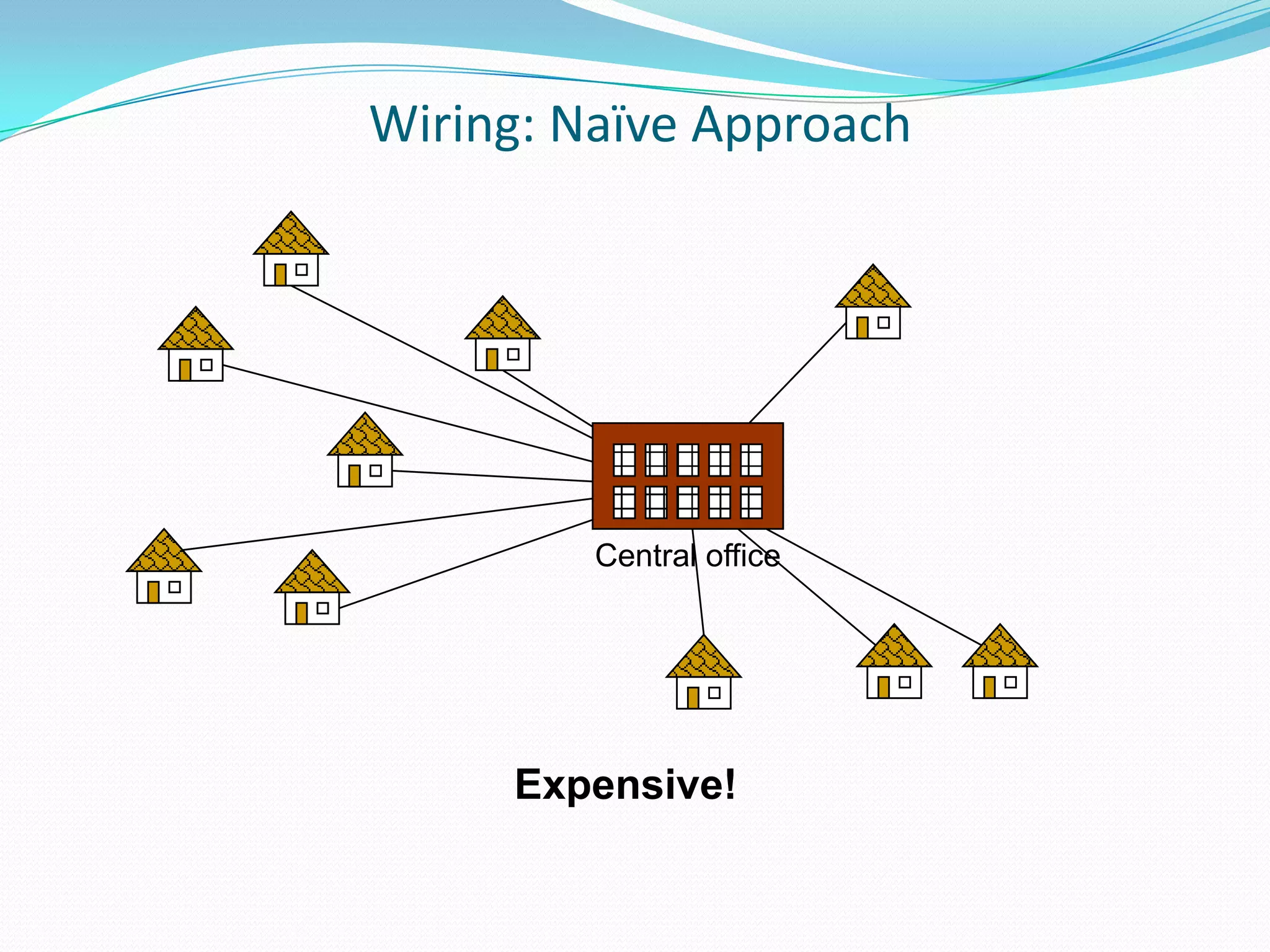
This document discusses minimum spanning trees. It defines a minimum spanning tree as a spanning tree of a connected, undirected graph that has a minimum total cost among all spanning trees of that graph. The document provides properties of minimum spanning trees, including that they are acyclic, connect all vertices, and have n-1 edges for a graph with n vertices. Applications of minimum spanning trees mentioned include communication networks, power grids, and laying telephone wires to minimize total length.

2. CONTENTS
 Tree
 Minimum spanning tree
 Definition
 Properties
 Example
 Applications

3. Tree
A tree is a graph with the following properties:
 The graph is connected (can go from anywhere to anywhere)
 There are no cycles(acyclic)
Tree Graphs that are not trees

4. Minimum Spanning Tree (MST)
Let G=(V,E) be an undirected connected graph.
A sub graph T=(V,E’) of G is a spanning tree of G iff T is
a tree.
• It is a tree (i.e., it is acyclic)
• It covers all the vertices V
• contains |V| - 1 edges
• A single graph can have many different spanning
trees.
4

5. Connected undirected graph Spanning trees

6.  A minimum cost spanning tree is a spanning tree which has a
minimum total cost.
 A minimum spanning tree (MST) or minimum weight spanning
tree is then a spanning tree with weight less than or equal to the
weight of every other spanning tree.
 Addition of even one single edge results in the spanning tree losing its
property of acyclicity and removal of one single edge results in its
losing the property of connectivity.
 It is the shortest spanning tree .
 The length of a tree is equal to the sum of the length of the arcs on the
tree.

7. Properties
Possible multiplicity
 There may be several minimum spanning trees of the same weight
having a minimum number of edges
 if all the edge weights of a given graph are the same, then every
spanning tree of that graph is minimum.
 If there are n vertices in the graph, then each tree has n-1 edges.
Uniqueness
 If each edge has a distinct weight then there will be only one, unique
minimum spanning tree.

8. Cycle Property:
 Let T be a minimum spanning tree of a weighted graph G
 Let e be an edge of G that is not in T and let C be the cycle formed
by e with T
 For every edge f of C, weight(f)  weight(e)
 If weight(f) > weight(e) we can get a spanning tree of smaller weight
by replacing e with f
f 8
f 8 Replacing f with e 4
4 yields C
C 9
9 2 6
2 6 a better spanning tree 3
3 e
e 8 7
8 7
7 7

9. Partition Property:
 Consider a partition of the vertices
of G into subsets U and V U V
f 7
 Let e be an edge of minimum weight
across the partition 4
9
 There is a minimum spanning tree 5
2
of G containing edge e 8
8 e 3
Proof: 7
 Let T be an MST of G
Replacing f with e
 If T does not contain e, consider the yields
cycle C formed by e with T and let f another MST
be an edge of C across the partition U V
f 7
 By the cycle property, 4
weight(f)  weight(e) 9
 Thus, weight(f) = weight(e) 2 5
8
 We obtain another MST by replacing
8 e 3
f with e
7

10. Minimum-cost spanning trees
 If we have a connected undirected graph with a weight (or cost)
associated with each edge
 The cost of a spanning tree would be the sum of the costs of its edges
 A minimum-cost spanning tree is a spanning tree that has the lowest
cost
16 16
A B A B
21 11 6 11 6
19 5 5
F C F C
33 14
10 18
E 18 D E D
A connected, undirected A minimum-cost spanning tree
graph

11. Applications of minimum spanning trees
 Consider an application where n stations are to be linked using a
communication network.
 The laying of communication links between any two stations involves a
cost.
 The problem is to obtain a network of communication links which
while preserving the connectivity between stations does it with
minimum cost.
 The ideal solution to the problem would be to extract a sub graph
termed minimum cost spanning tree.
 It preserves the connectedness of the graph yields minimum cost.

12. Applications cont’d
• Suppose you want to supply a set of houses with:
 electric power
 water
 sewage lines
 telephone lines
• To keep costs down, you could connect these houses with
a spanning tree ( for example, power lines)
•However, the houses are not all equal distances apart
• To reduce costs even further, you could connect the
houses with a minimum-cost spanning tree

13. Applications cont’d
• Constructing highways or railroads spanning several
cities
• Designing local access network
• Making electric wire connections on a control panel
• Laying pipelines connecting offshore drilling sites,
refineries, and consumer markets

14. Applications cont’d
 The phone company task is to provide phone lines to a village with 10
houses, each labeled H1 through H10.
 A single cable must connects each home. The cable must run through
houses H1, H2, and so forth, up through H10.
 Each node is a house, and the edges are the means by which one house
can be wired up to another.
 The weights of the edges dictate the distance between the homes.
 Their task is to wire up all ten houses using the least amount of
telephone wiring possible.

15. Graphical representation of hooking up a 10-home village with
phone lines

16.  The two valid spanning trees from the above graph.
 The edges forming the spanning tree are bolded.

17. Problem: Laying Telephone Wire
Central office

18. Wiring: Naïve Approach
Central office
Expensive!

19. Wiring: Better Approach
Central office
Minimize the total length of wire connecting the customers

20. Thank you