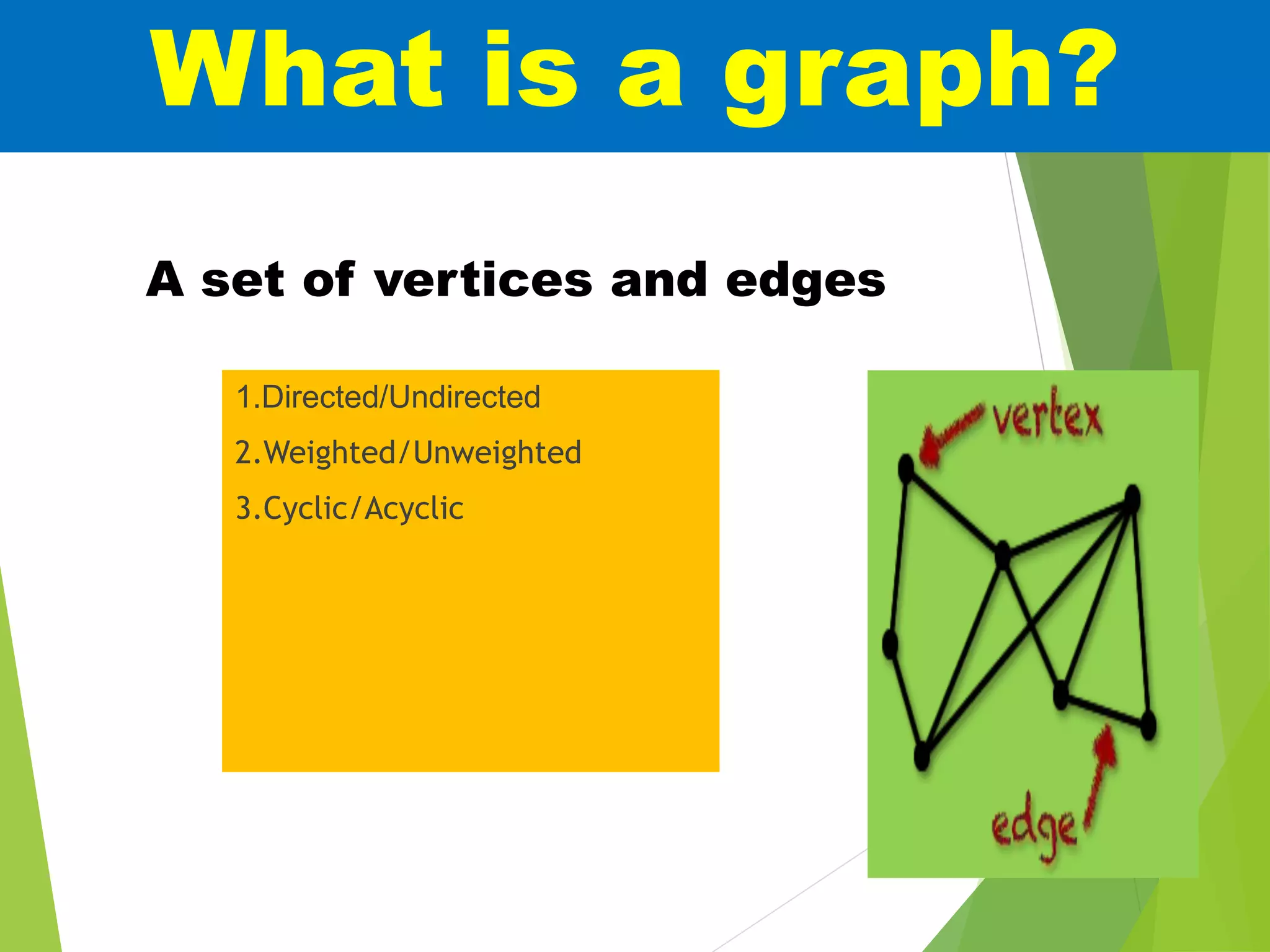
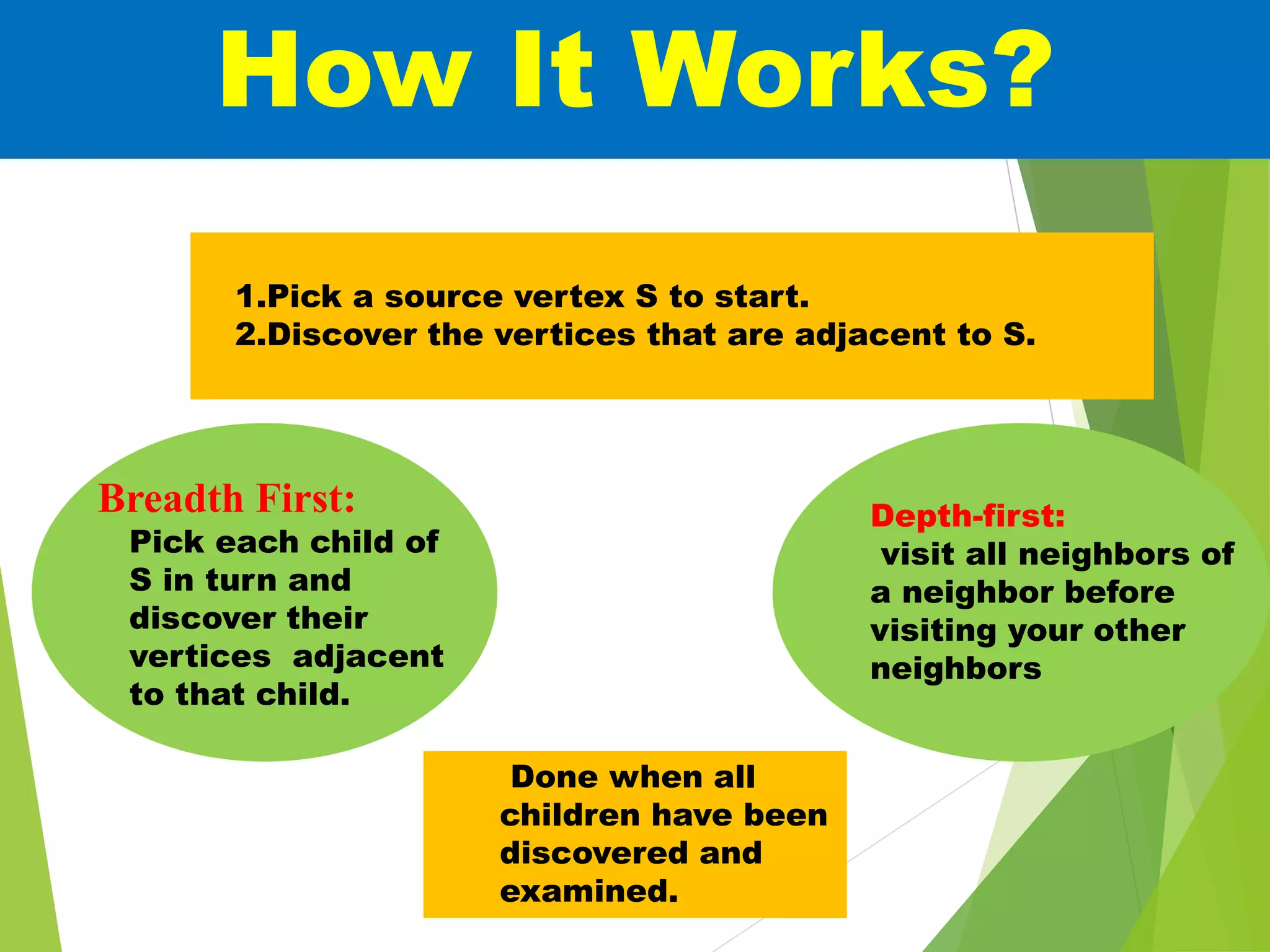
The document discusses graph traversal algorithms breadth-first search (BFS) and depth-first search (DFS). It provides examples of how BFS and DFS work, including pseudocode for algorithms. It also discusses applications of BFS such as finding shortest paths and detecting bipartitions. Applications of DFS include finding connected components and topological sorting.

1. Welcome To Our Presentation

2. Group Name : Quantative

3.  Depth First Search (DFS)
 Breadth First Search (BFS)
Topics

4. What is a graph?
1.Directed/Undirected
2.Weighted/Unweighted
3.Cyclic/Acyclic
A set of vertices and edges

5.  Breadth First Search (BFS)
Start several paths at a time, and advance in each one step at a time
The breadth-first search uses a FIFO queue.
 Depth First Search (DFS)
Once a possible path is found, continue the search until the end of the path
The Depth-first search uses a LIFO Stack.
Graph Traversal

6. How It Works?
1.Pick a source vertex S to start.
2.Discover the vertices that are adjacent to S.
Depth-first:
visit all neighbors of
a neighbor before
visiting your other
neighbors
Breadth First:
Pick each child of
S in turn and
discover their
vertices adjacent
to that child.
Done when all
children have been
discovered and
examined.

7. For a Graph G=(V, E) and n = |V| and m=|E|
When Adjacency List is used Complexity is O(m + n)
When Adjacency Matrix is used Scanning each row for
checking the connectivity of a Vertex is in order O(n).
So, Complexity is O(n2 )
DFS uses space O(|V|) in the worst case to store the
stack of vertices on the current search path as well as
the set of already-visited vertices.
Analysis of DFS

8. Example:

9. Depth-first search: Directed
graphs
 The algorithm is essentially the same as for undirected
graphs, the difference residing in the interpretation of the
word "adjacent".
 In a directed graph, node w is adjacent to node v if the
directed edge (v, w) exists.
 If (v, w) exists but (w, v) does not, then w is adjacent to v
but v is not adjacent to w.
 With this change of interpretation the procedures dfs and
search apply equally well in the case of a directed graph.

10. DFS Example
Data Structure and Algorithm
source
vertex

11. DFS Example
Data Structure and Algorithm
1 | | |
|||
| |
source
vertex
d f

12. DFS Example
Data Structure and Algorithm
1 | | |
|||
2 | |
source
vertex
d f

13. DFS Example
Data Structure and Algorithm
1 | | |
||3 |
2 | |
source
vertex
d f

14. DFS Example
Data Structure and Algorithm
1 | | |
||3 | 4
2 | |
source
vertex
d f

15. DFS Example
Data Structure and Algorithm
1 | | |
|5 |3 | 4
2 | |
source
vertex
d f

16. DFS Example
Data Structure and Algorithm
1 | | |
|5 | 63 | 4
2 | |
source
vertex
d f

17. DFS Example
Data Structure and Algorithm
1 | | |
|5 | 63 | 4
2 | 7 |
source
vertex
d f

18. DFS Example
Data Structure and Algorithm
1 | 8 | |
|5 | 63 | 4
2 | 7 |
source
vertex
d f

19. DFS Example
Data Structure and Algorithm
1 | 8 | |
|5 | 63 | 4
2 | 7 9 |
source
vertex
d f

20. DFS Example
Data Structure and Algorithm
1 | 8 | |
|5 | 63 | 4
2 | 7 9 |10
source
vertex
d f

21. DFS Example
Data Structure and Algorithm
1 | 8 |11 |
|5 | 63 | 4
2 | 7 9 |10
source
vertex
d f

22. DFS Example
Data Structure and Algorithm
1 |12 8 |11 |
|5 | 63 | 4
2 | 7 9 |10
source
vertex
d f

23. DFS Example
Data Structure and Algorithm
1 |12 8 |11 13|
|5 | 63 | 4
2 | 7 9 |10
source
vertex
d f

24. DFS Example
Data Structure and Algorithm
1 |12 8 |11 13|
14|5 | 63 | 4
2 | 7 9 |10
source
vertex
d f

25. DFS Example
Data Structure and Algorithm
1 |12 8 |11 13|
14|155 | 63 | 4
2 | 7 9 |10
source
vertex
d f

26. DFS Example
Data Structure and Algorithm
1 |12 8 |11 13|16
14|155 | 63 | 4
2 | 7 9 |10
source
vertex
d f

27. Algorithm steps
Step:1
Push the root node in stack.
Step:2
Loop until stack is empty.
Step:3
Peek the node of the stack.
Step:4
If the node has unvisited child nodes get the
unvisited child node mark it has travers and push it
on stack.

28. Data
Structure
and
Algorithm
DFS: Algorithm
DFS(G)
 for each vertex u in V,
 color[u]=white; p[u]=NIL
 time=0;
 for each vertex u in V
 if (color[u]=white)
 DFS-VISIT(u)

29. Data
Structure
and
Algorithm
DFS-VISIT(u)
 color[u]=gray;
 time = time + 1;
 d[u] = time;
 for each v in Adj(u) do
 if (color[v] = white)
 p[v] = u;
 DFS-VISIT(v);
 color[u] = black;
 time = time + 1; f[u]= time;
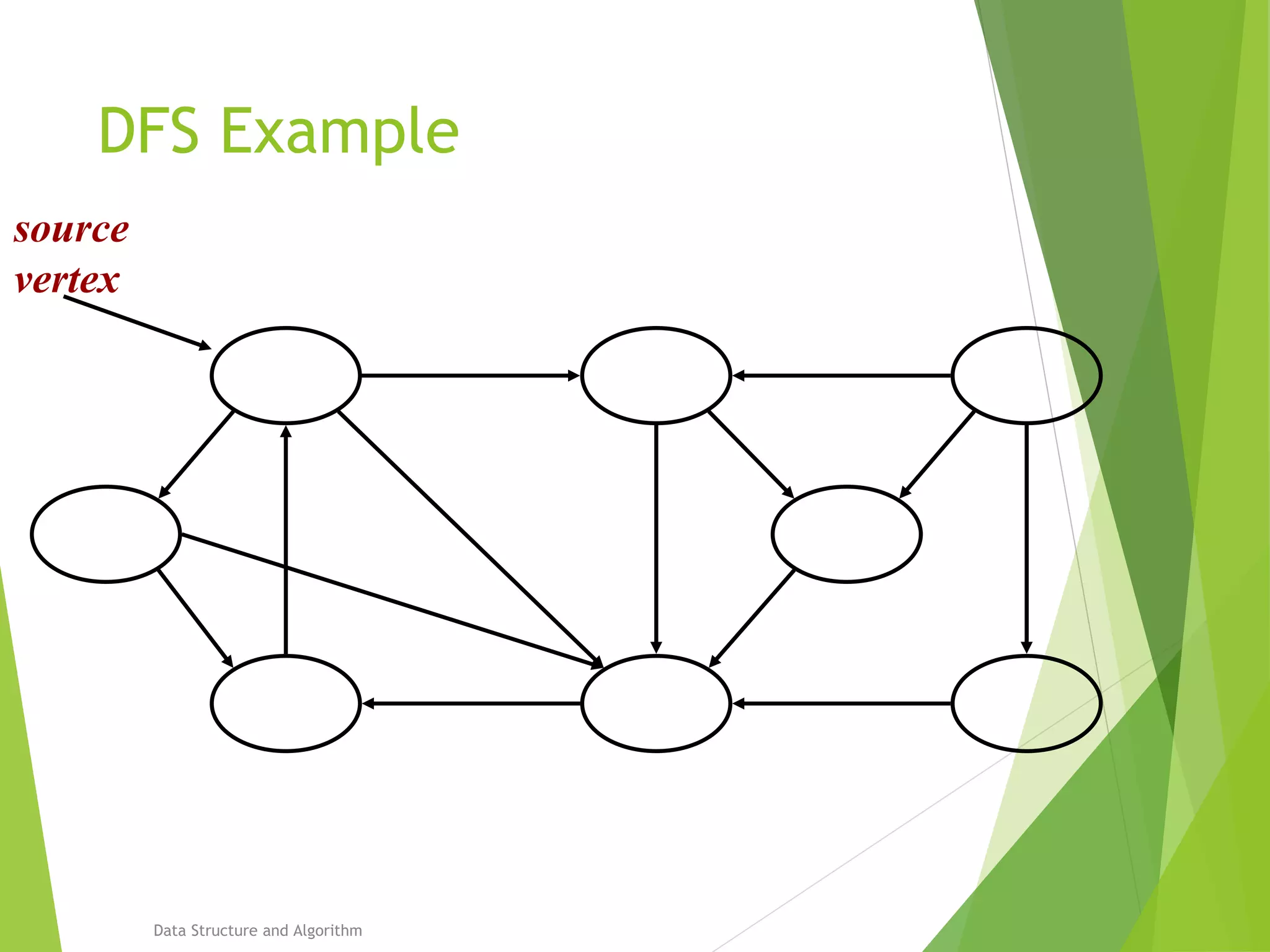
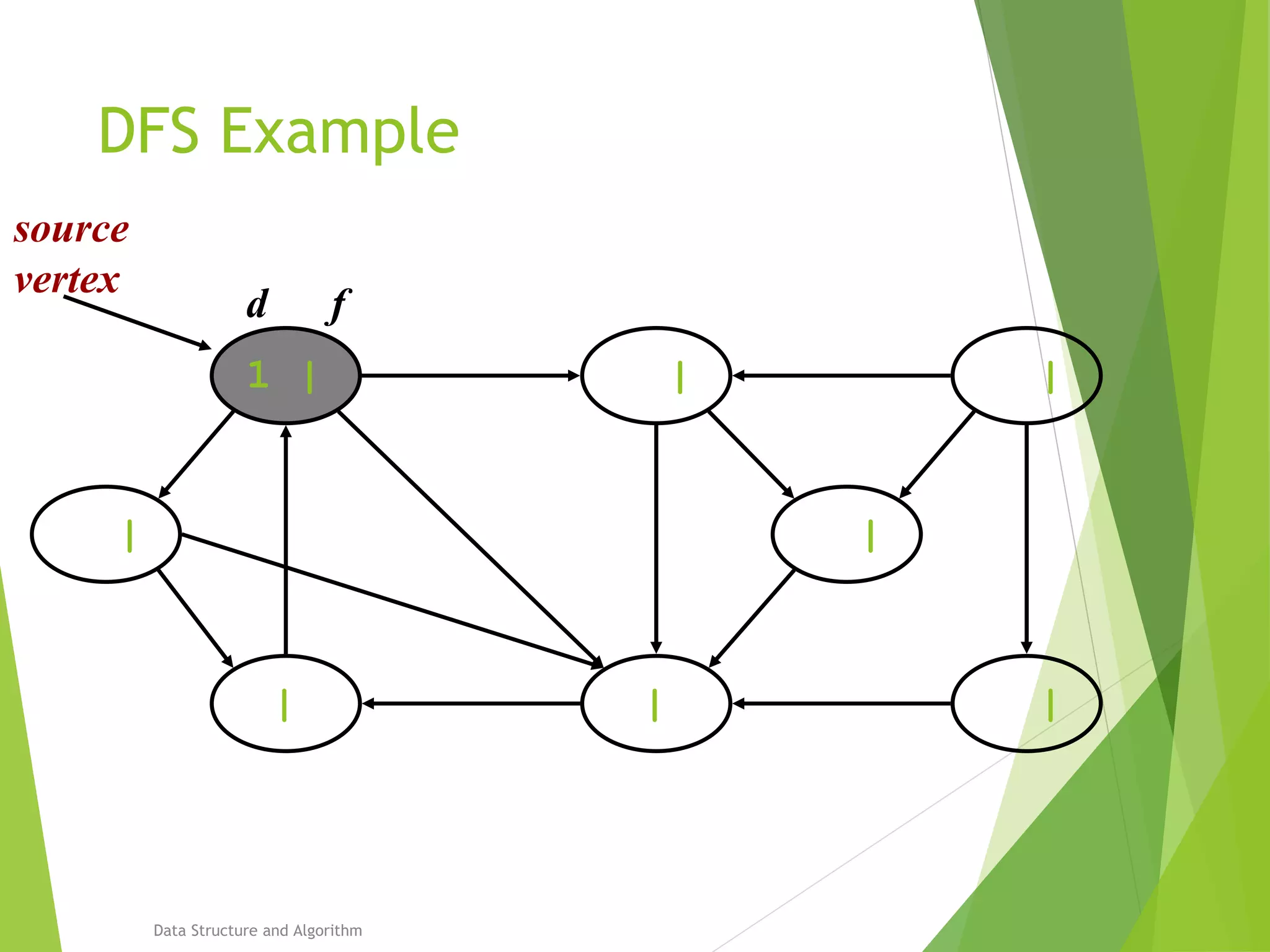
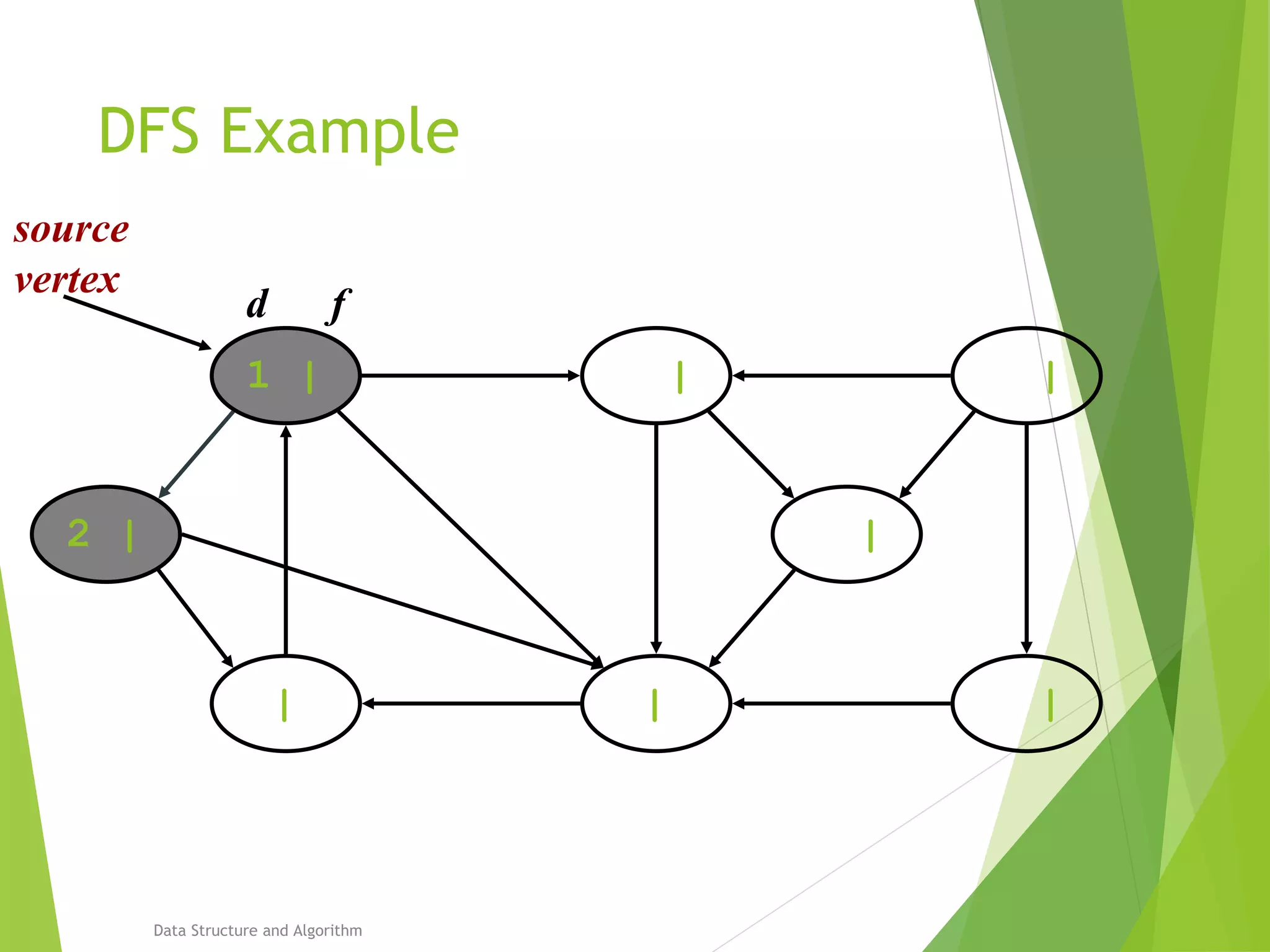
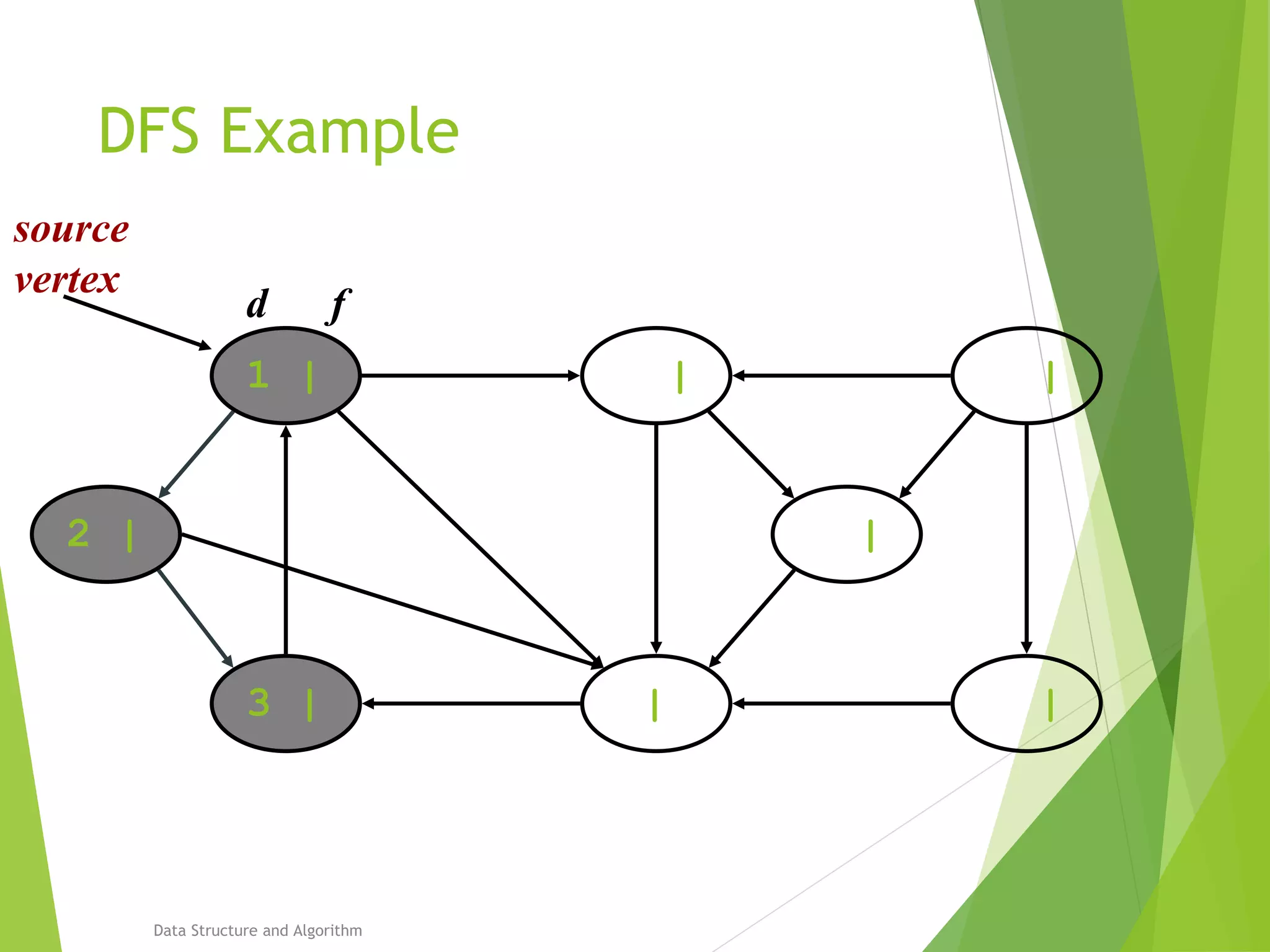
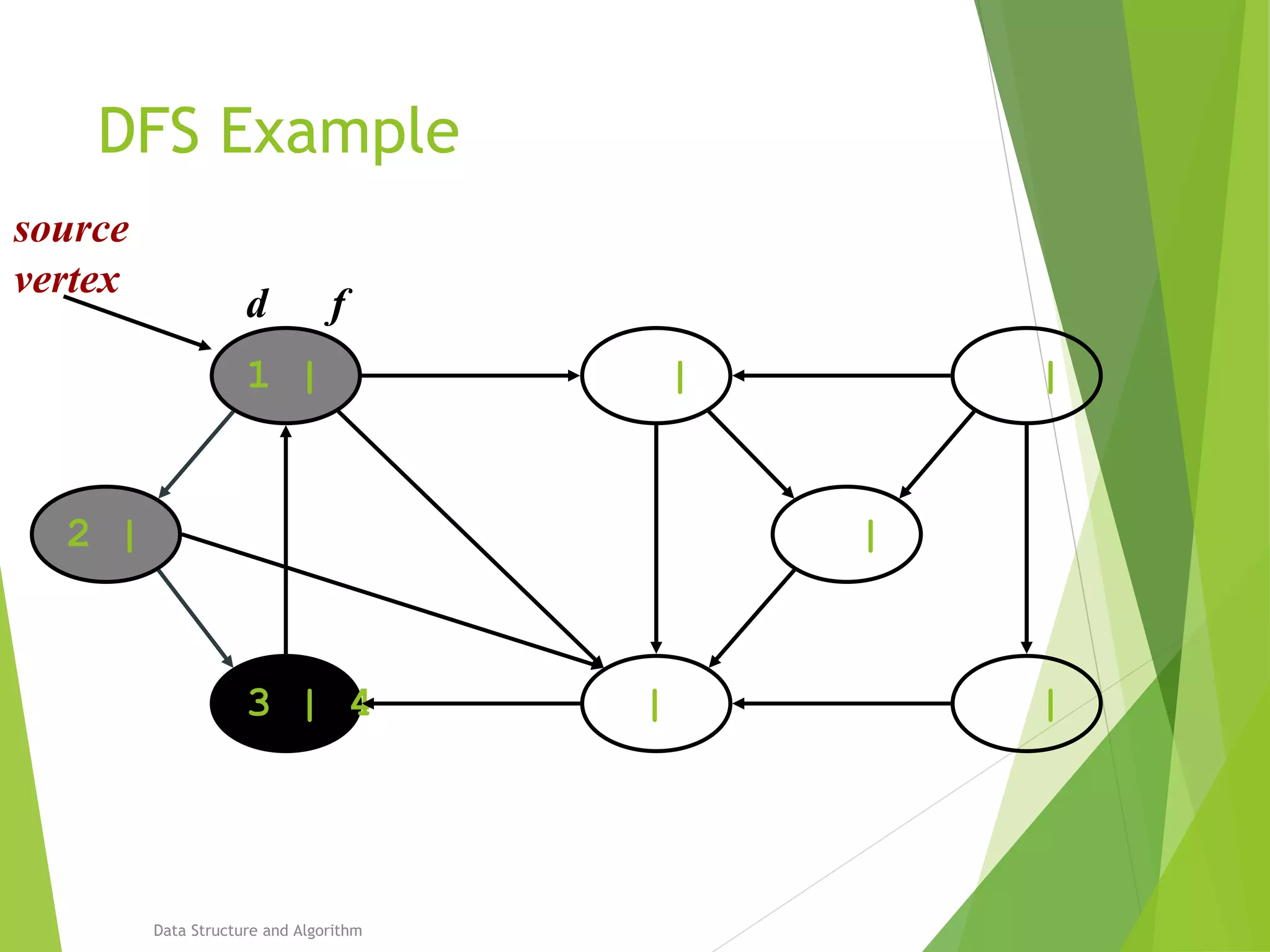
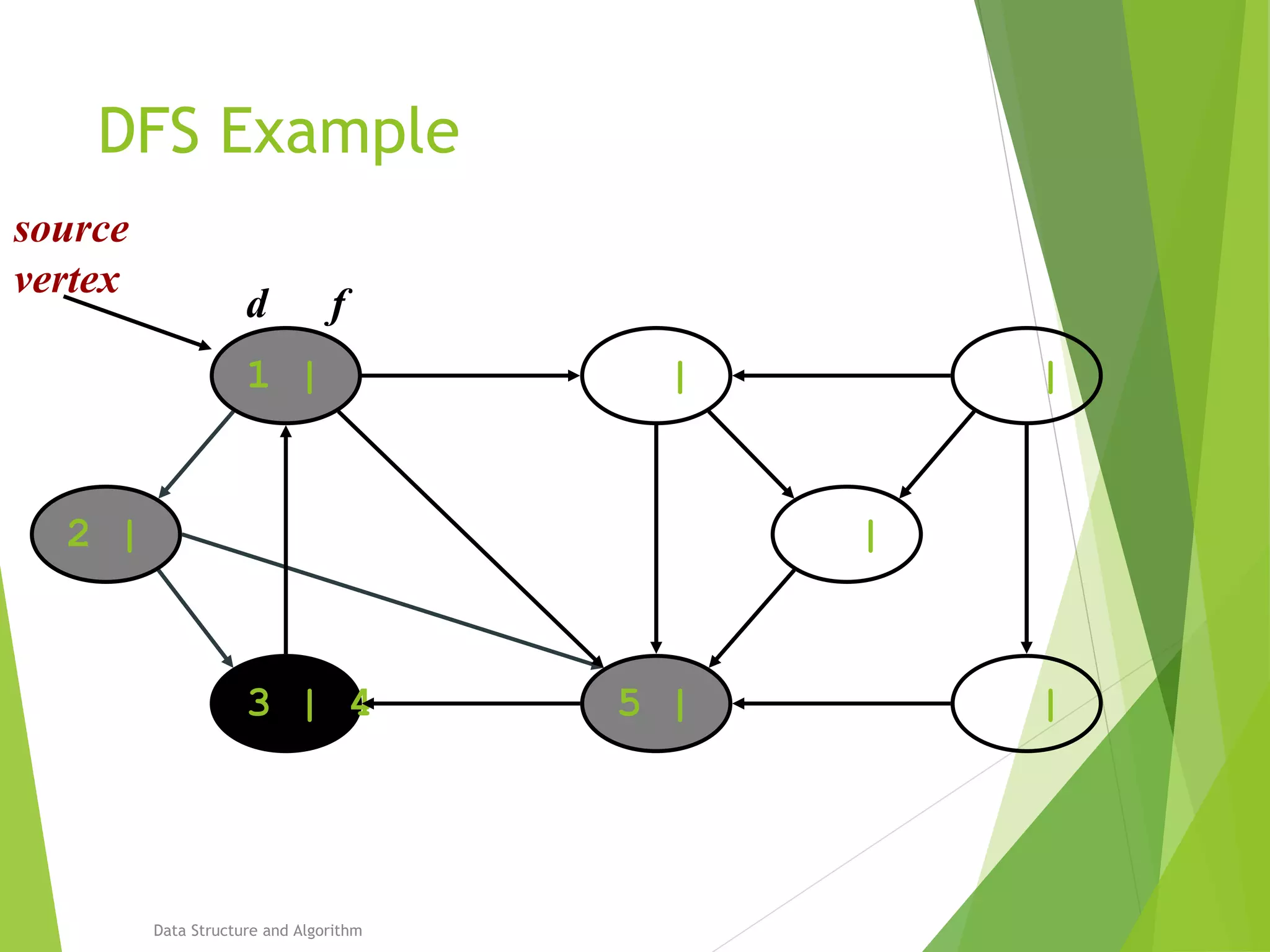
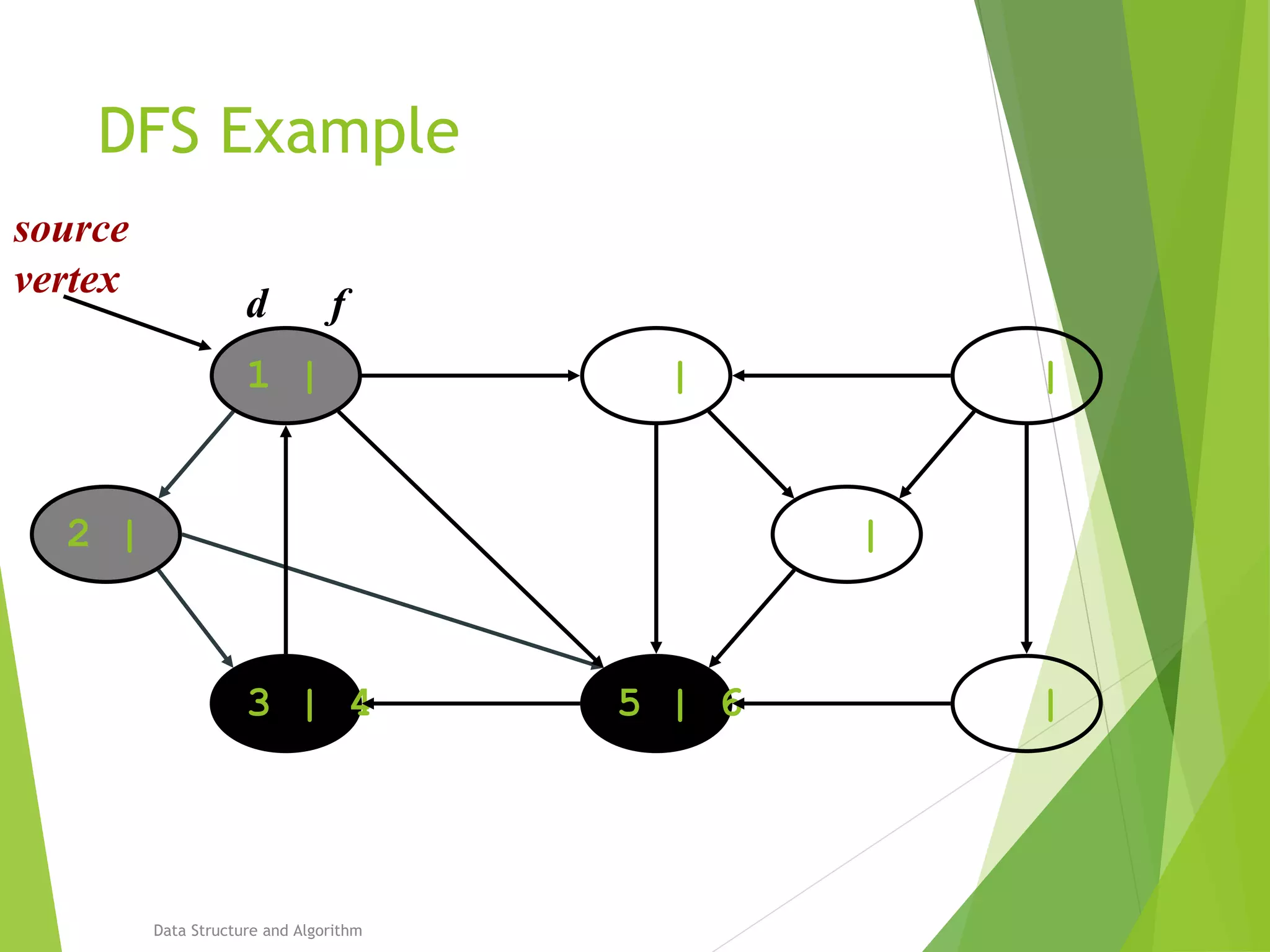
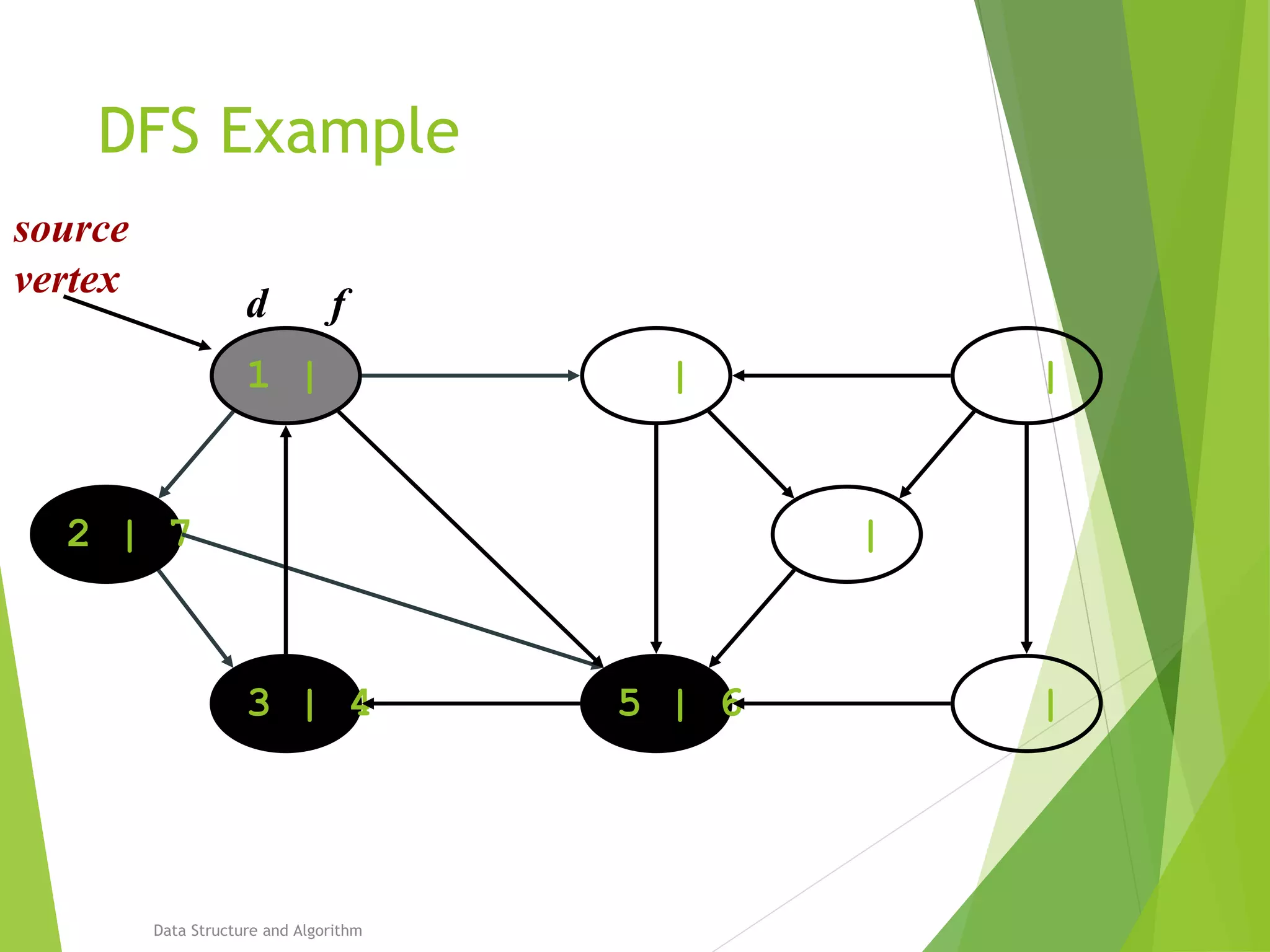
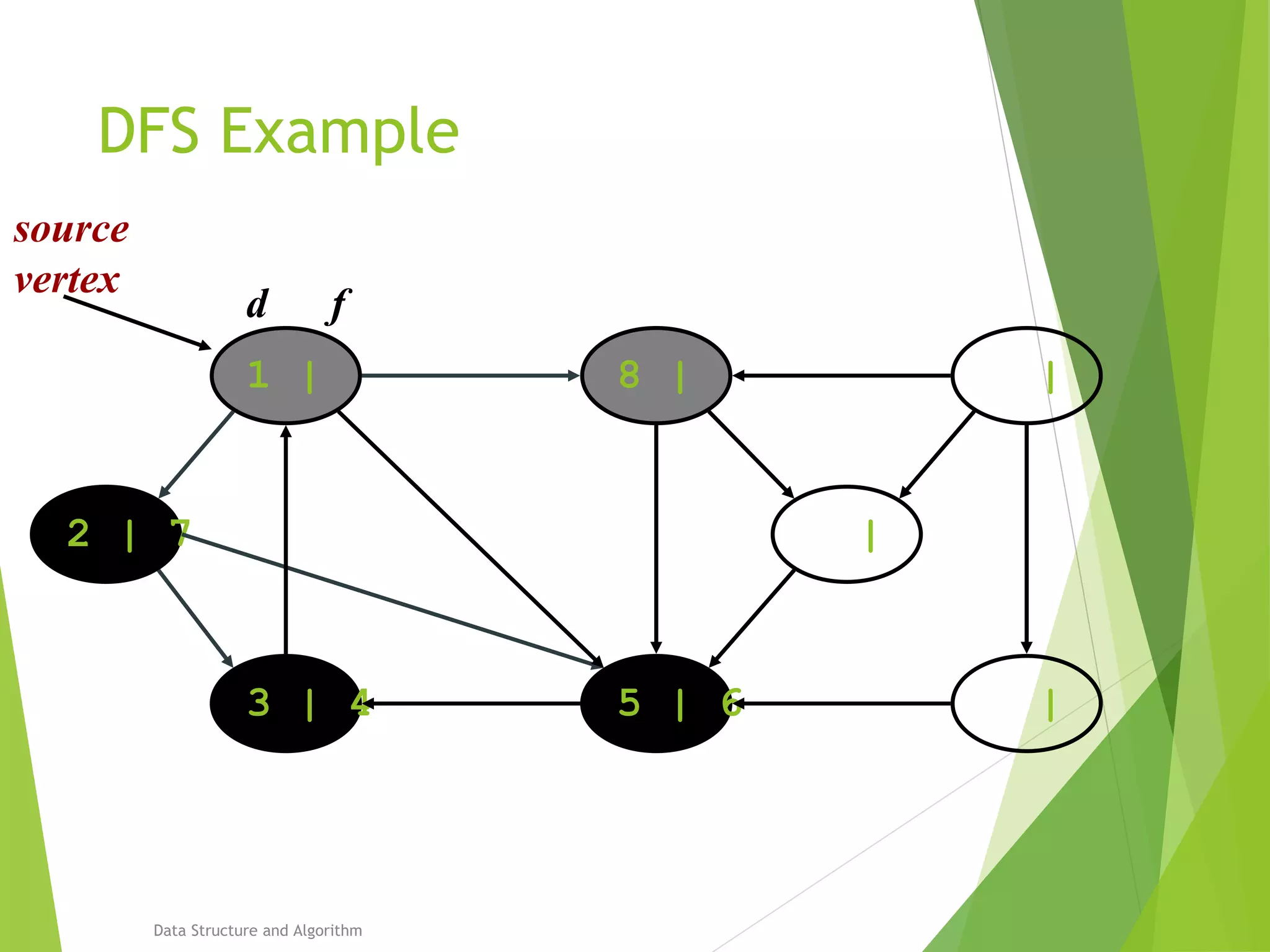
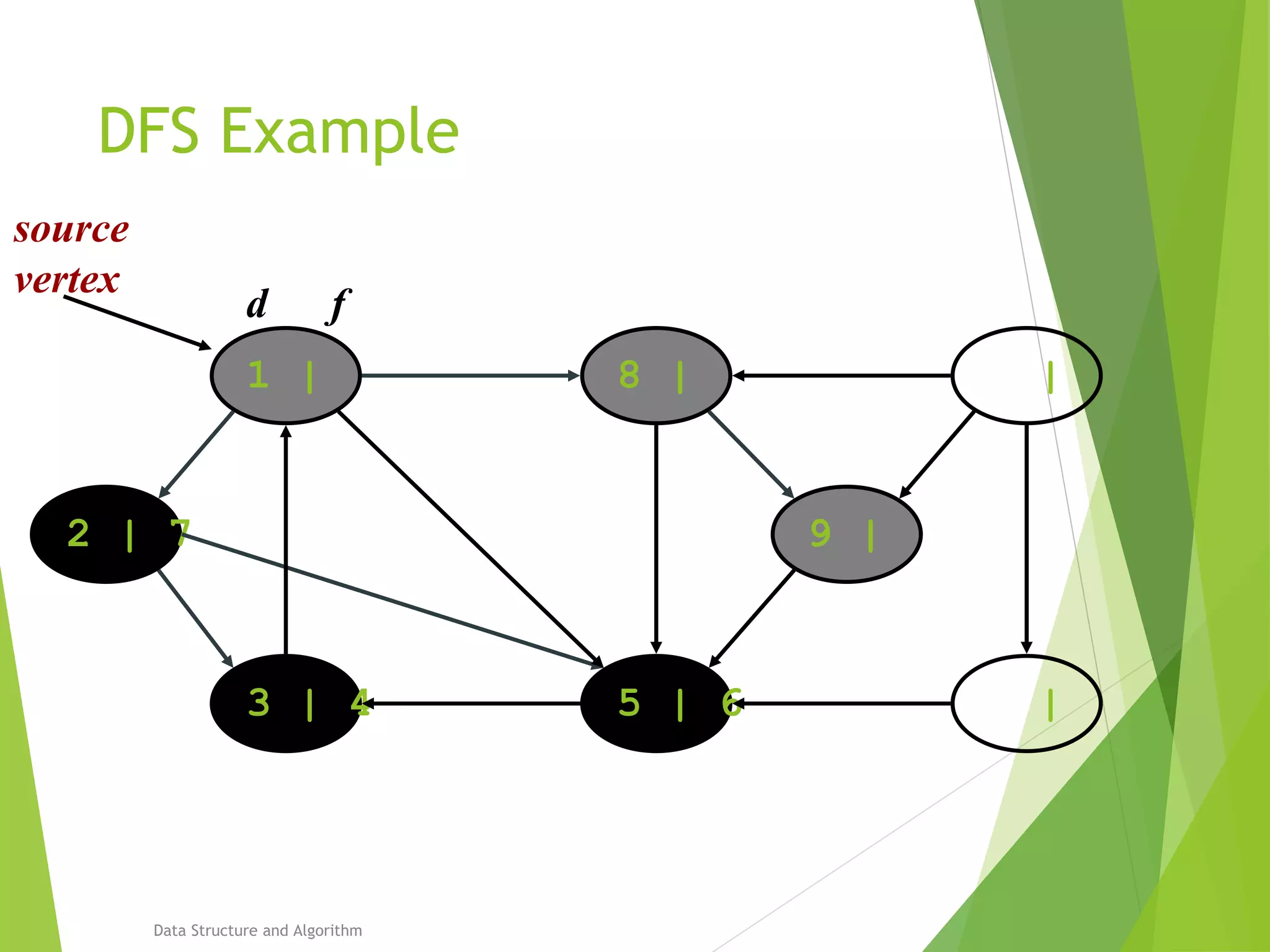
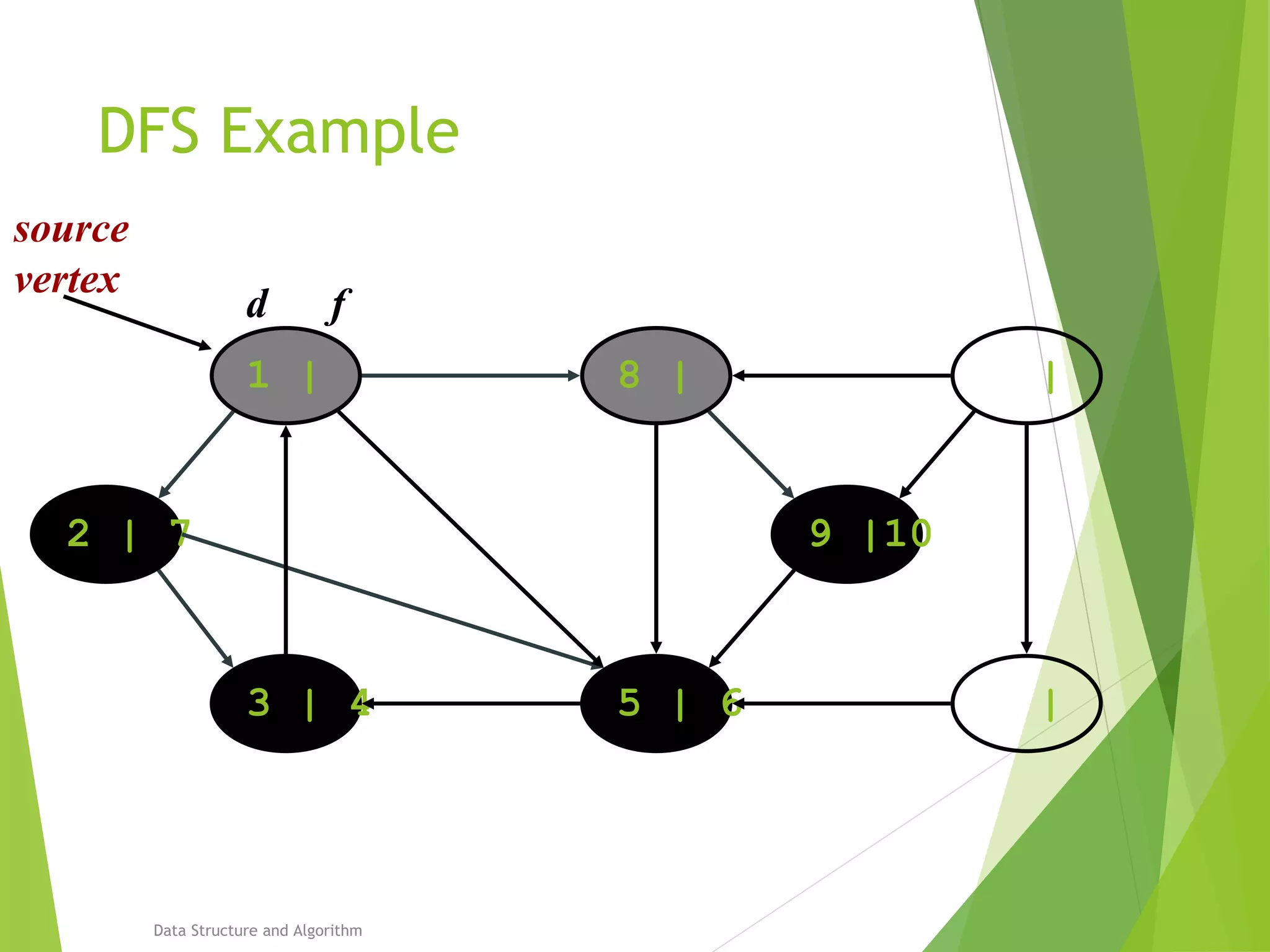
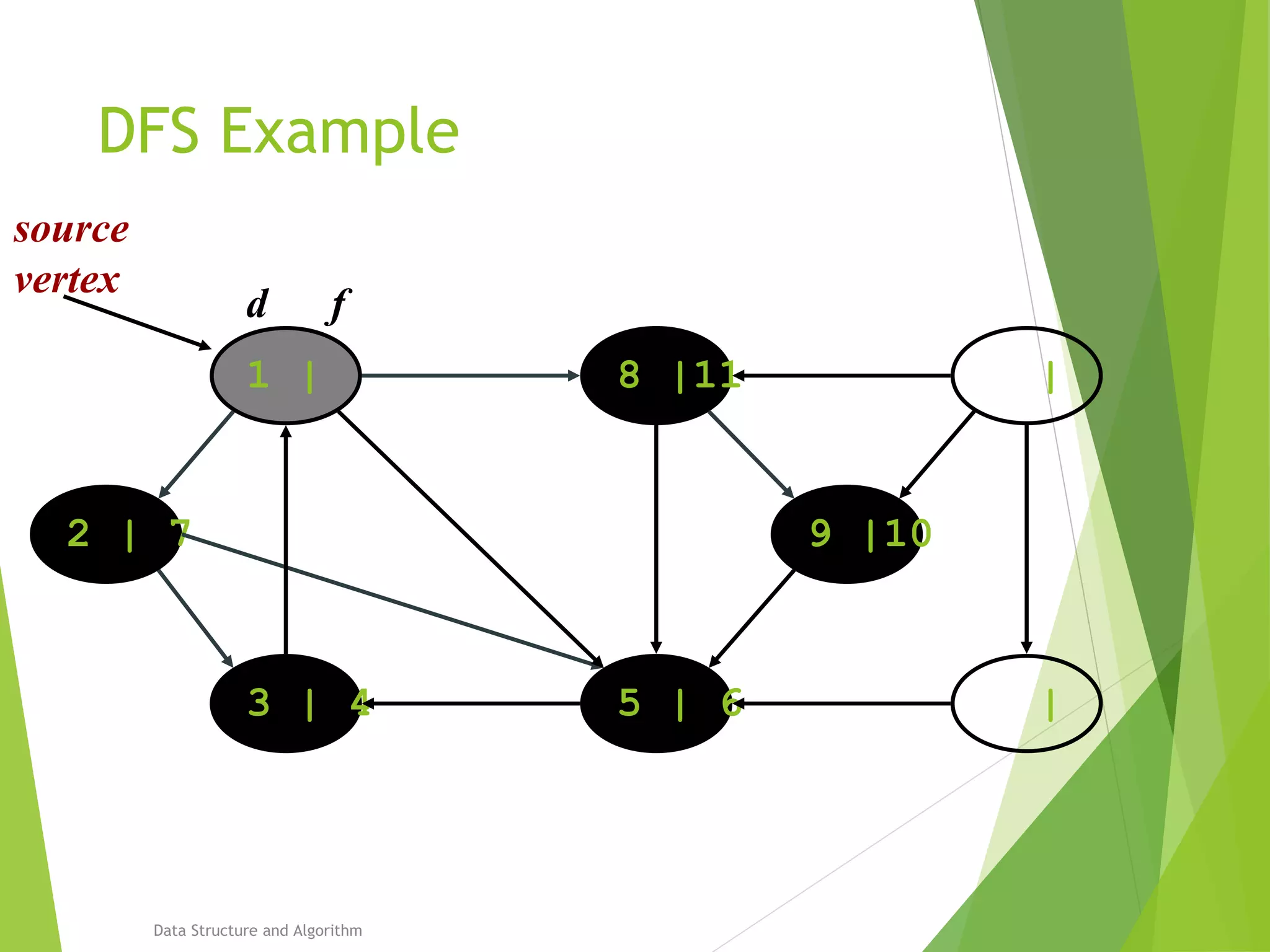
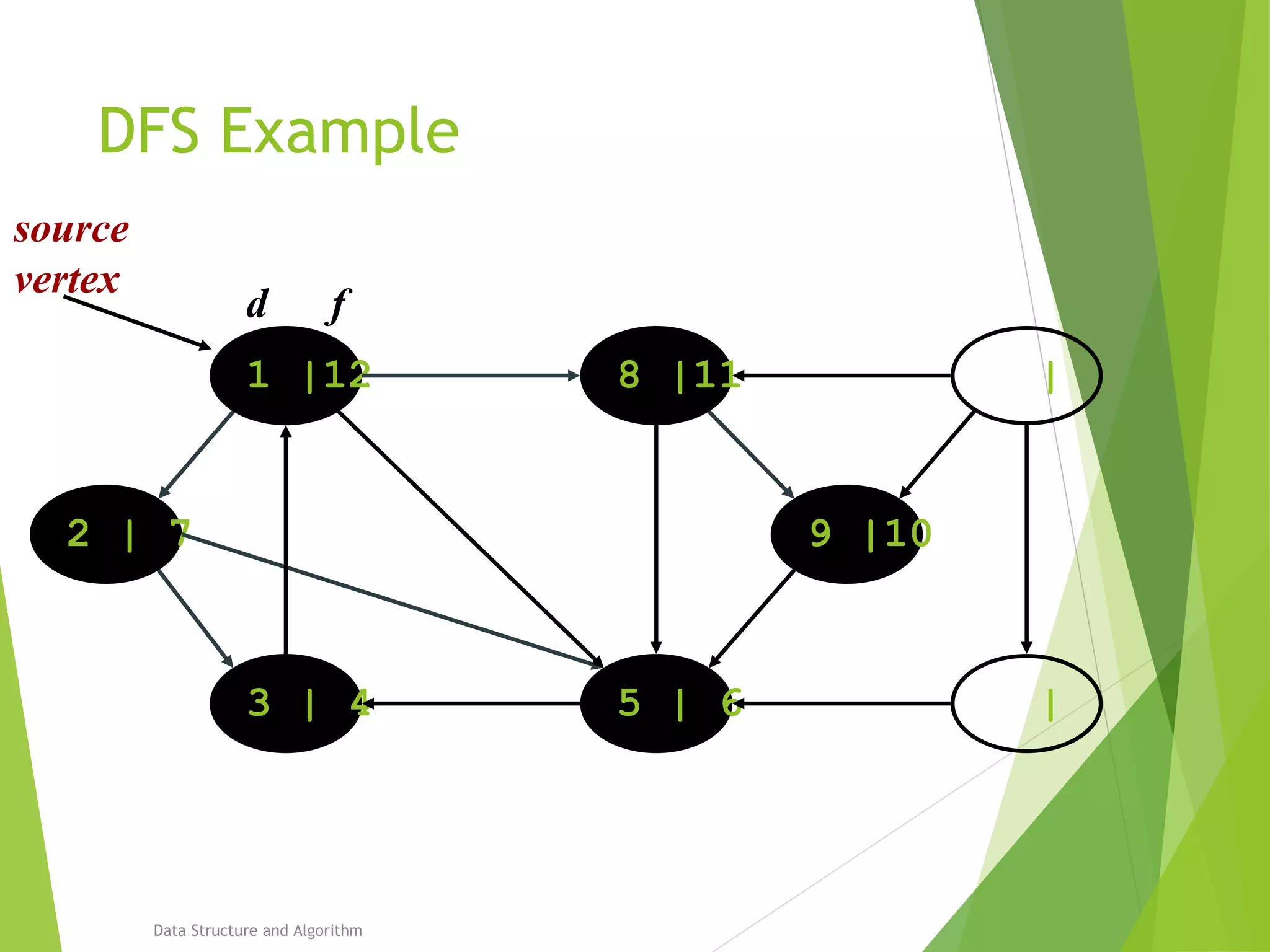
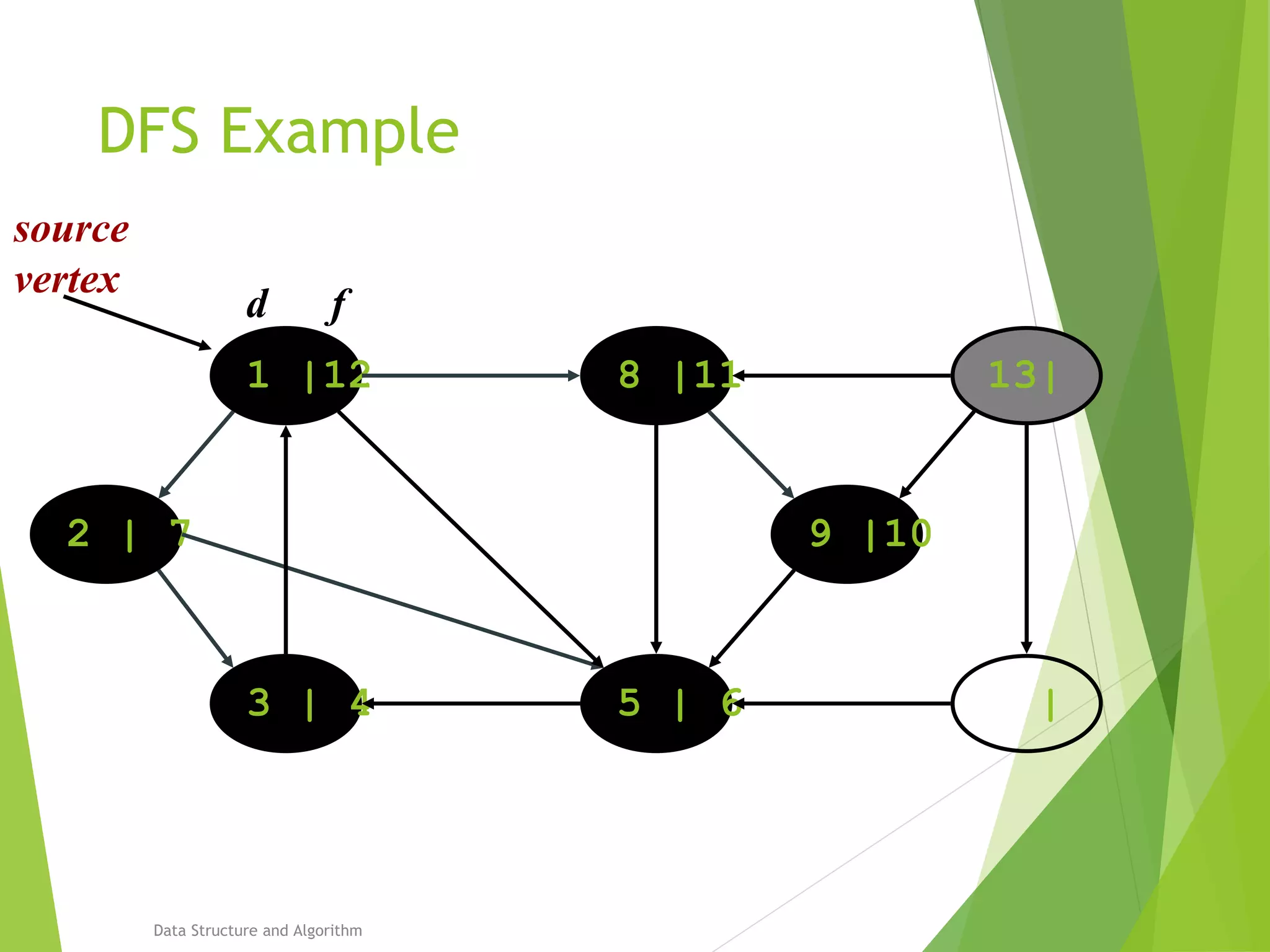
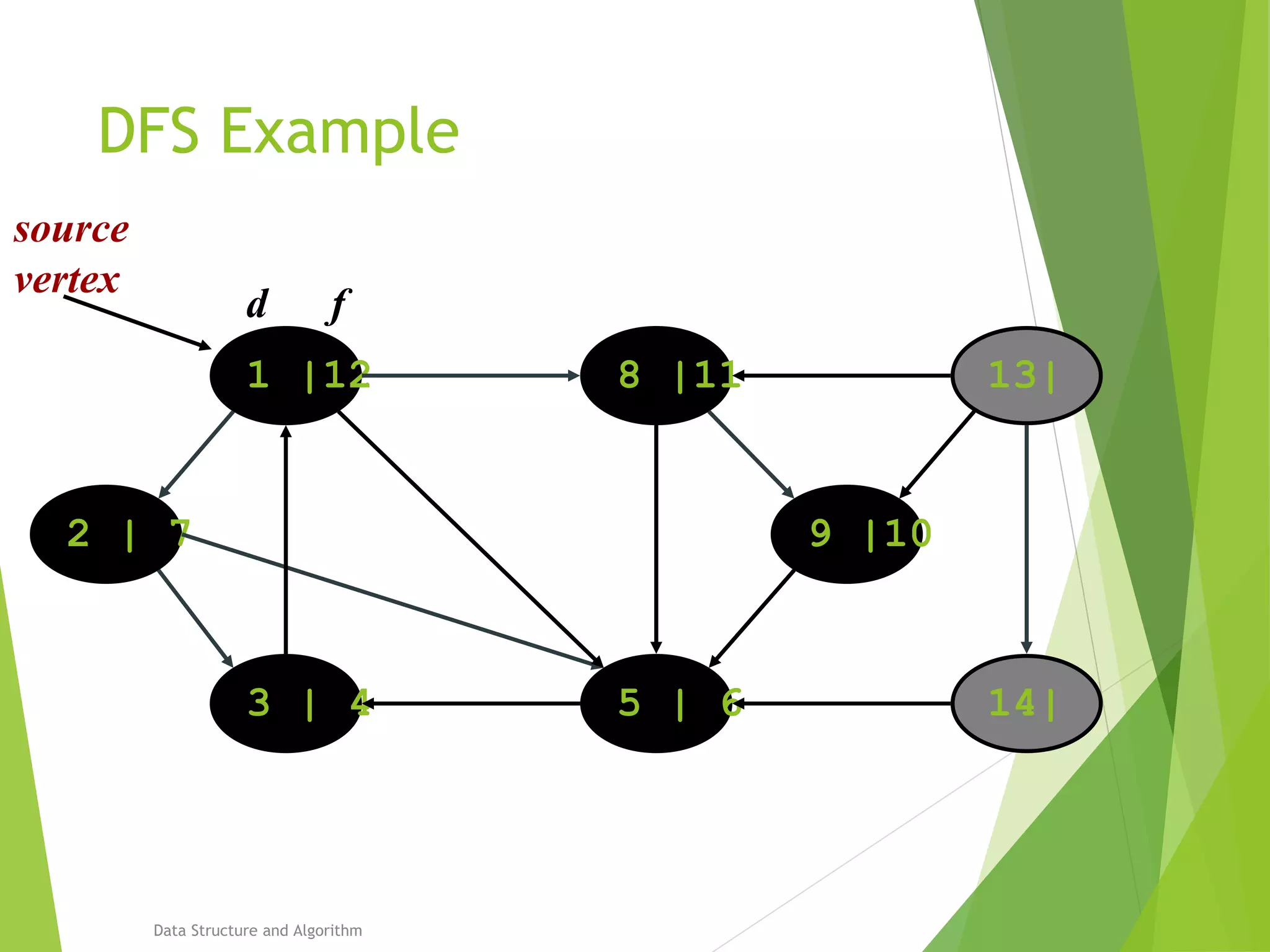
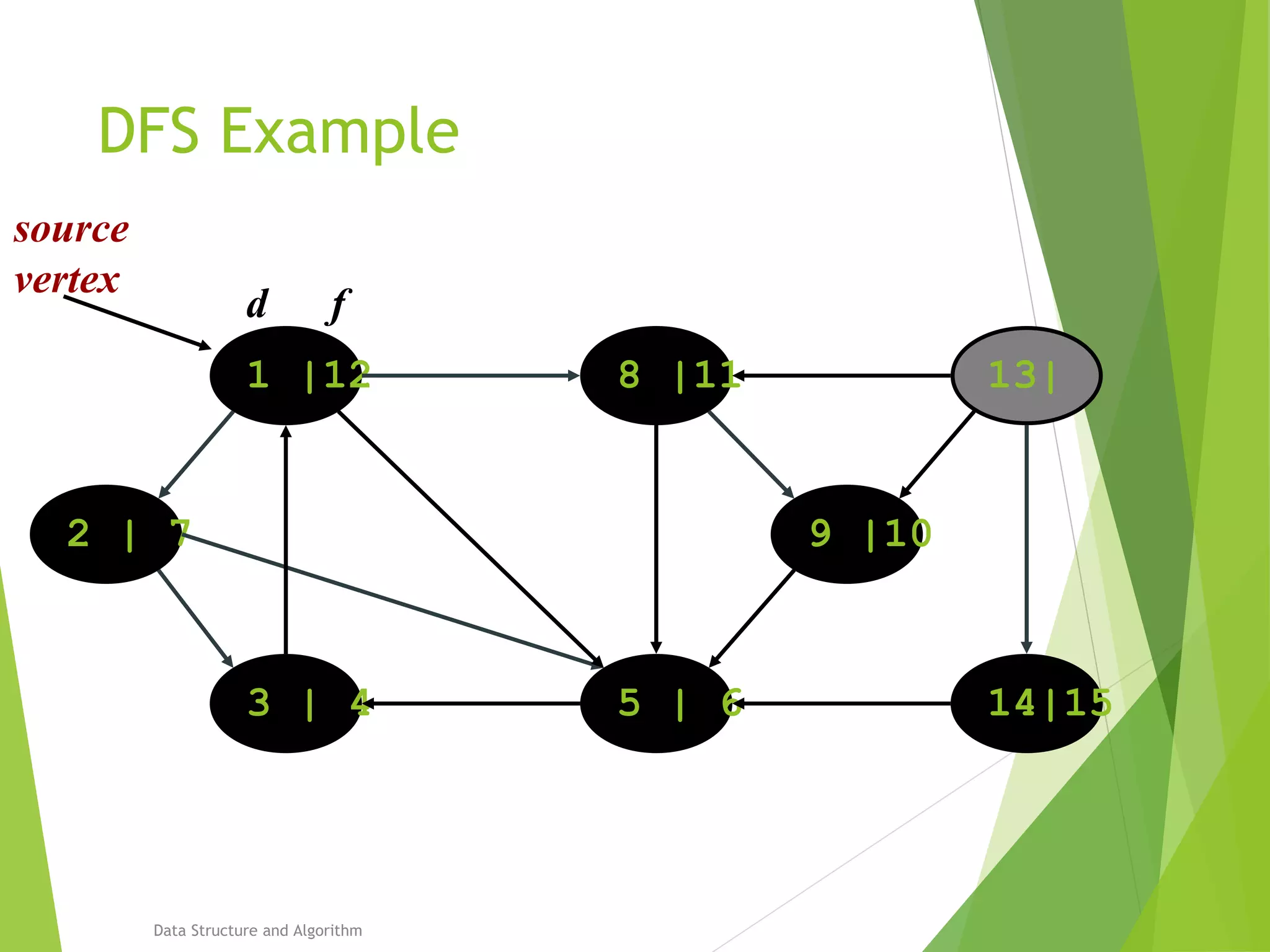
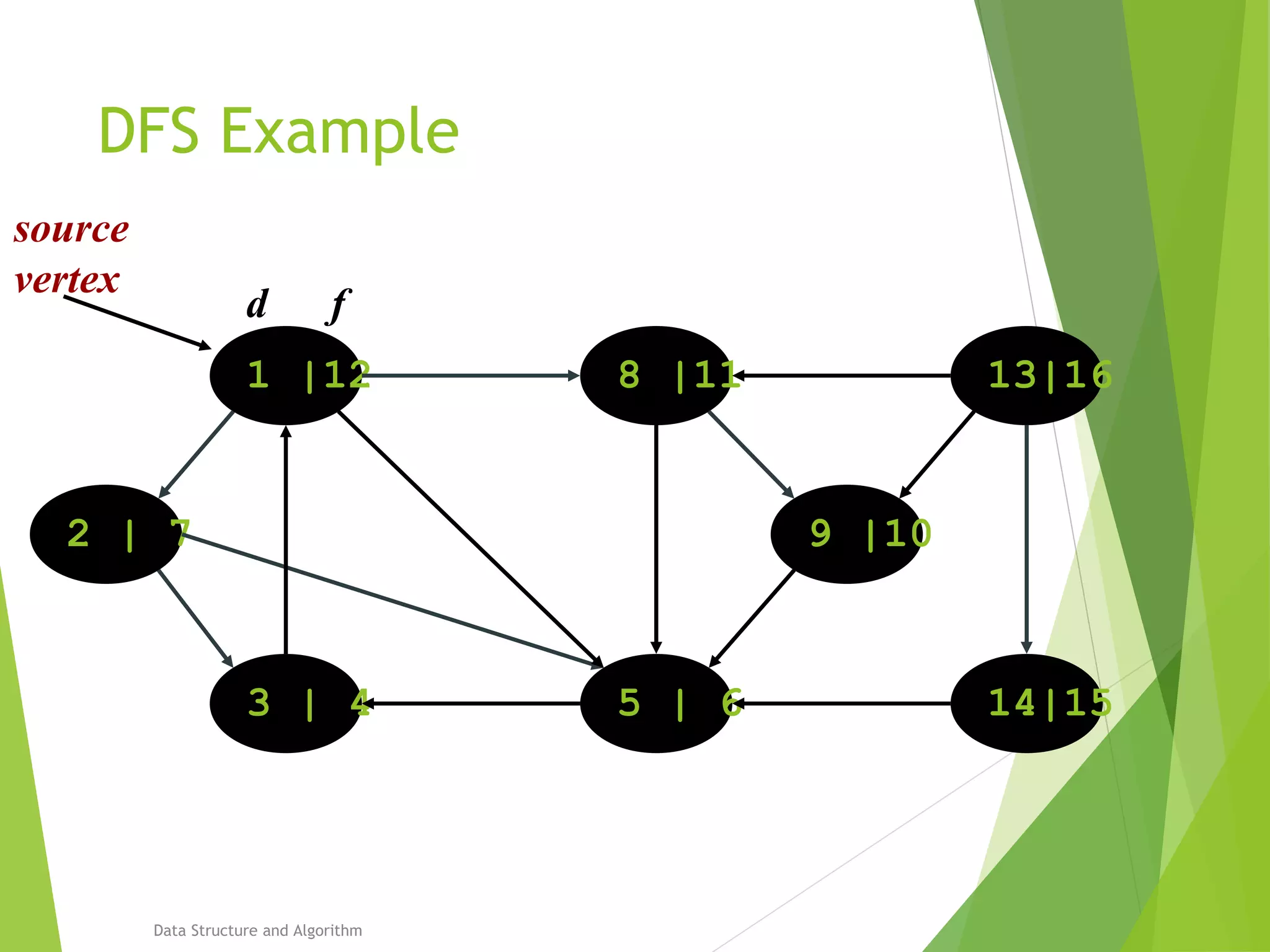
DFS: Algorithm (Cont.)
source
vertex

30. BFS:
*Testing a graph for bipartitions
*To find the shortest path from a vertex s to
a vertex v in an un weighted graph
*To find the length of such a path
*To find out if a graph contains cycles
*To construct a BSF tree/forest from a graph
*Copying garbage collection
Applications

31. Applications
DFS:
* Finding connected components.
*Topological sorting.
*Finding the bridges of a graph.
*cycle Detecting
*Finding strongly connected components.
*Finding biconnectivity in graphs.