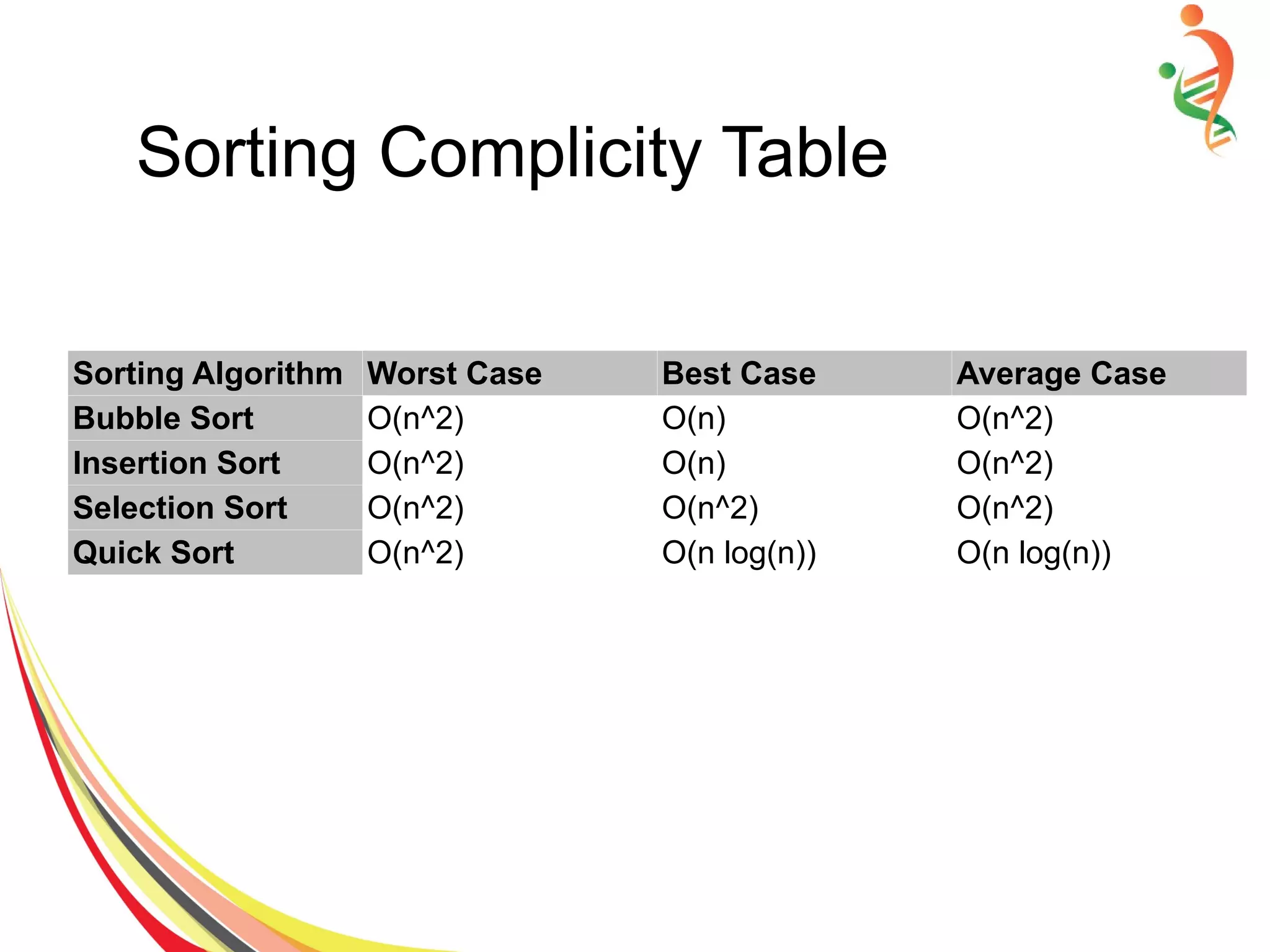
The document provides information on various sorting and searching algorithms, including bubble sort, insertion sort, selection sort, quick sort, sequential search, and binary search. It includes pseudocode to demonstrate the algorithms and example implementations with sample input data. Key points covered include the time complexity of each algorithm (O(n^2) for bubble/insertion/selection sort, O(n log n) for quick sort, O(n) for sequential search, and O(log n) for binary search) and how they work at a high level.

1. Sorting & Searching

2. Sorting & Searching
● Bubble Sort
● Insertion Sort
● Selection Sort
● Quick Sort
● Sequential Search
● Binary Search

3. Bubble Sort
● In bubble sort repeatedly move the largest
element to the highest index position of the array
and on each iteration to reduce the effective size
of the array.
● In Bubble sort we compare the adjacent item and
swap if required.
● In a bubble sorting algorithm, the elements of the
list "gradually 'bubble' (or rise) to their proper
location in the array, like bubbles rising in a glass
of soda"

4. Algorithm of Bubble Sort
● Declare array on n items
items[n]={4,5,1,8,54,32...32}
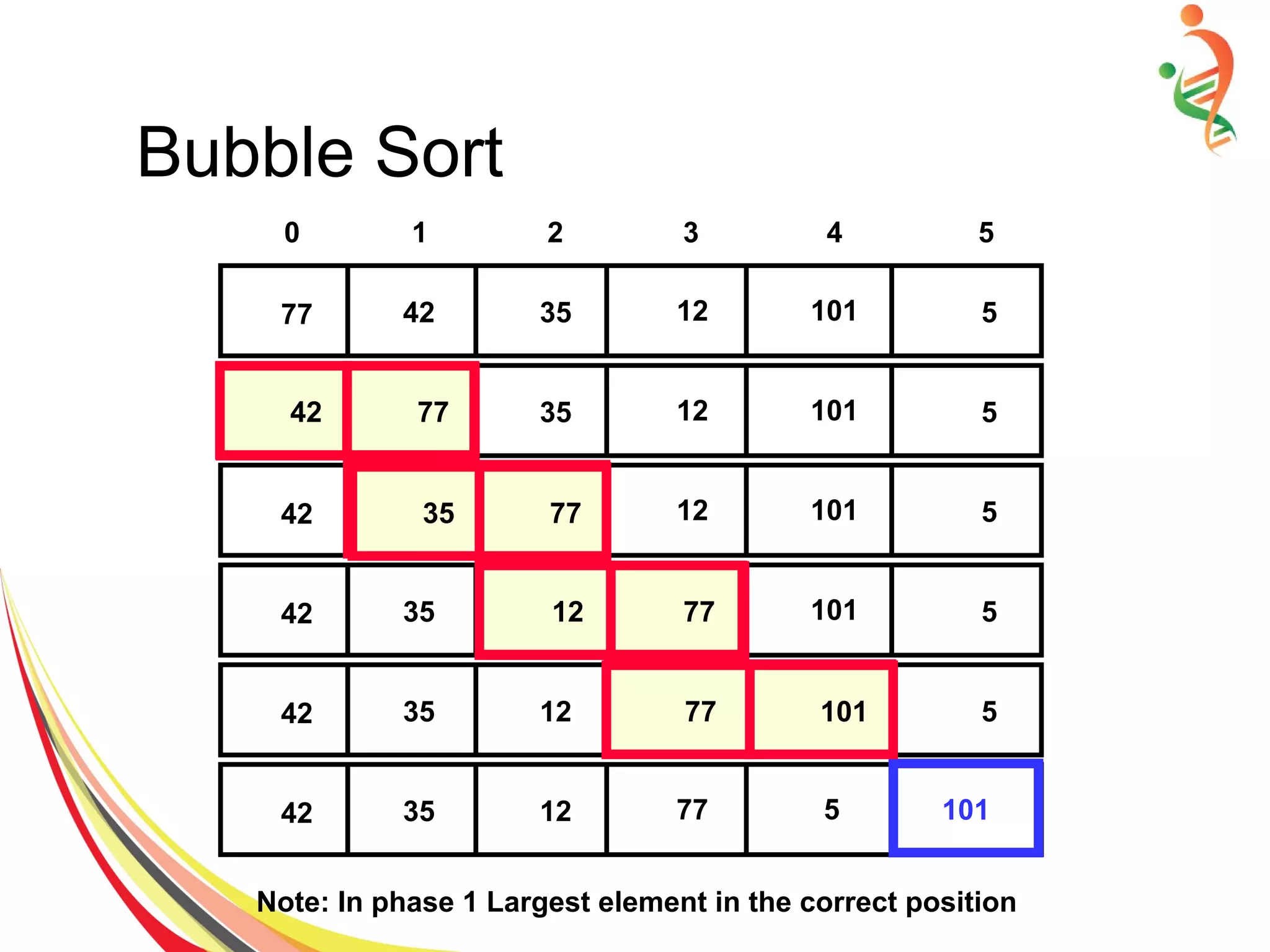
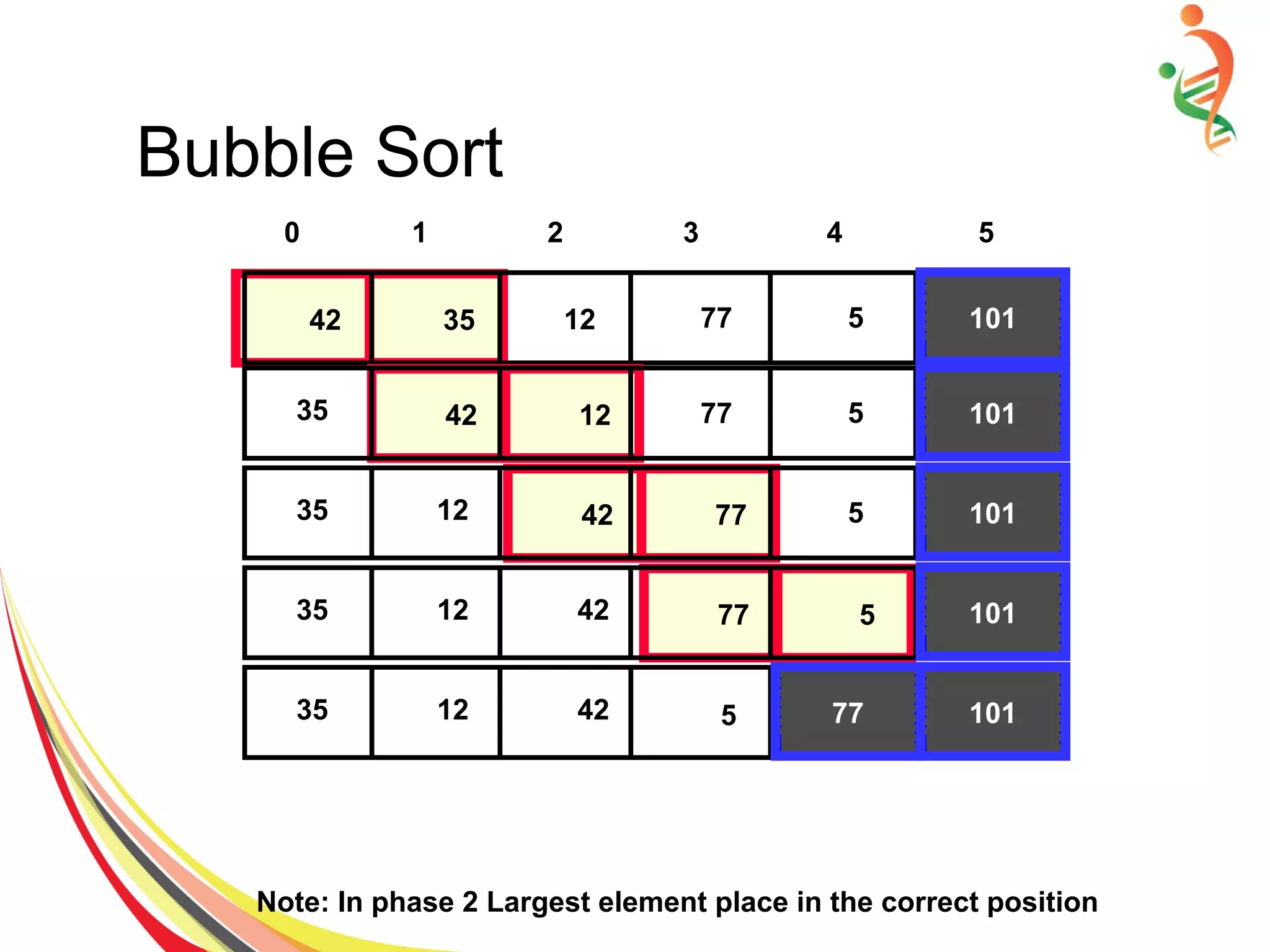
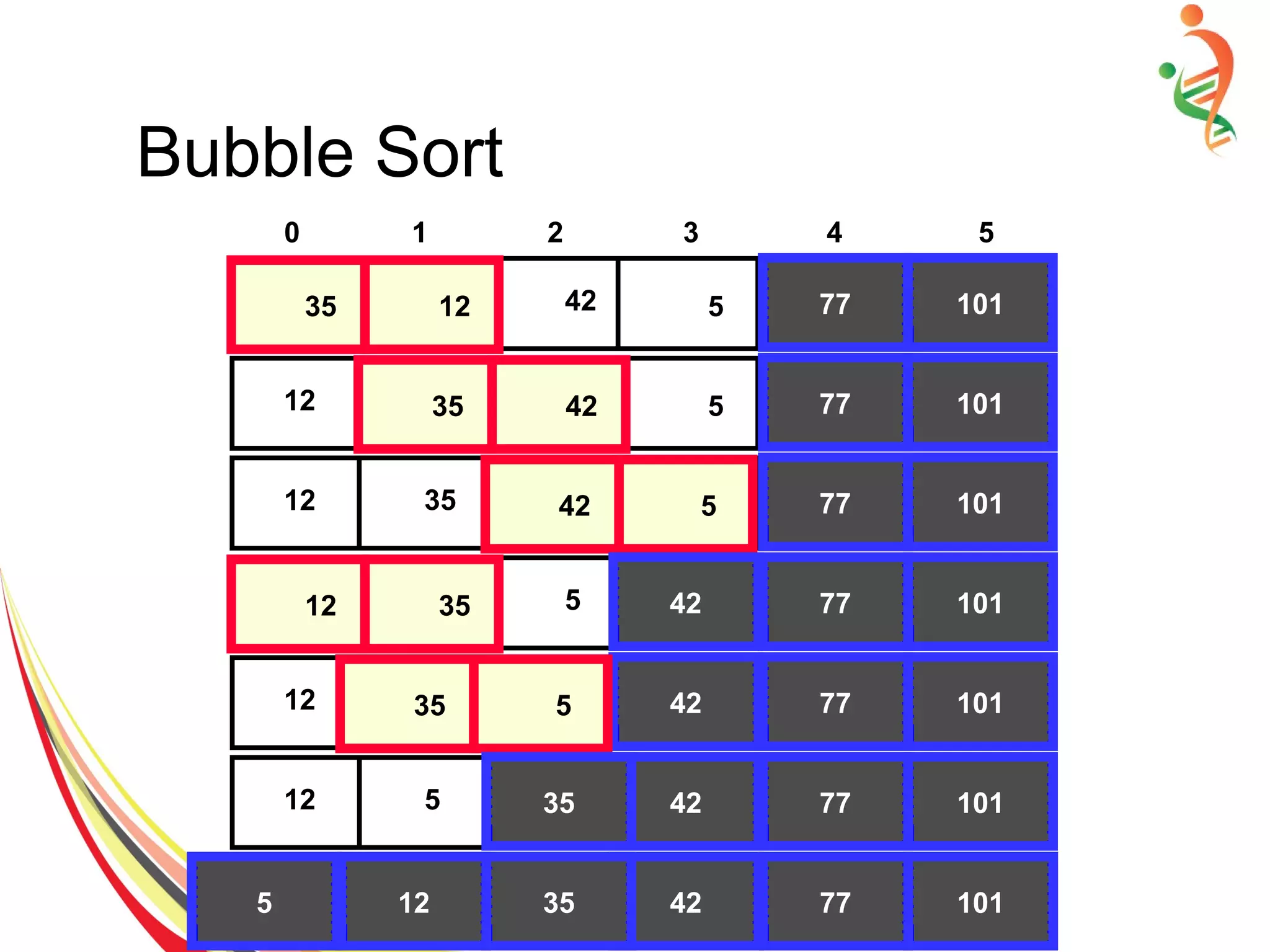
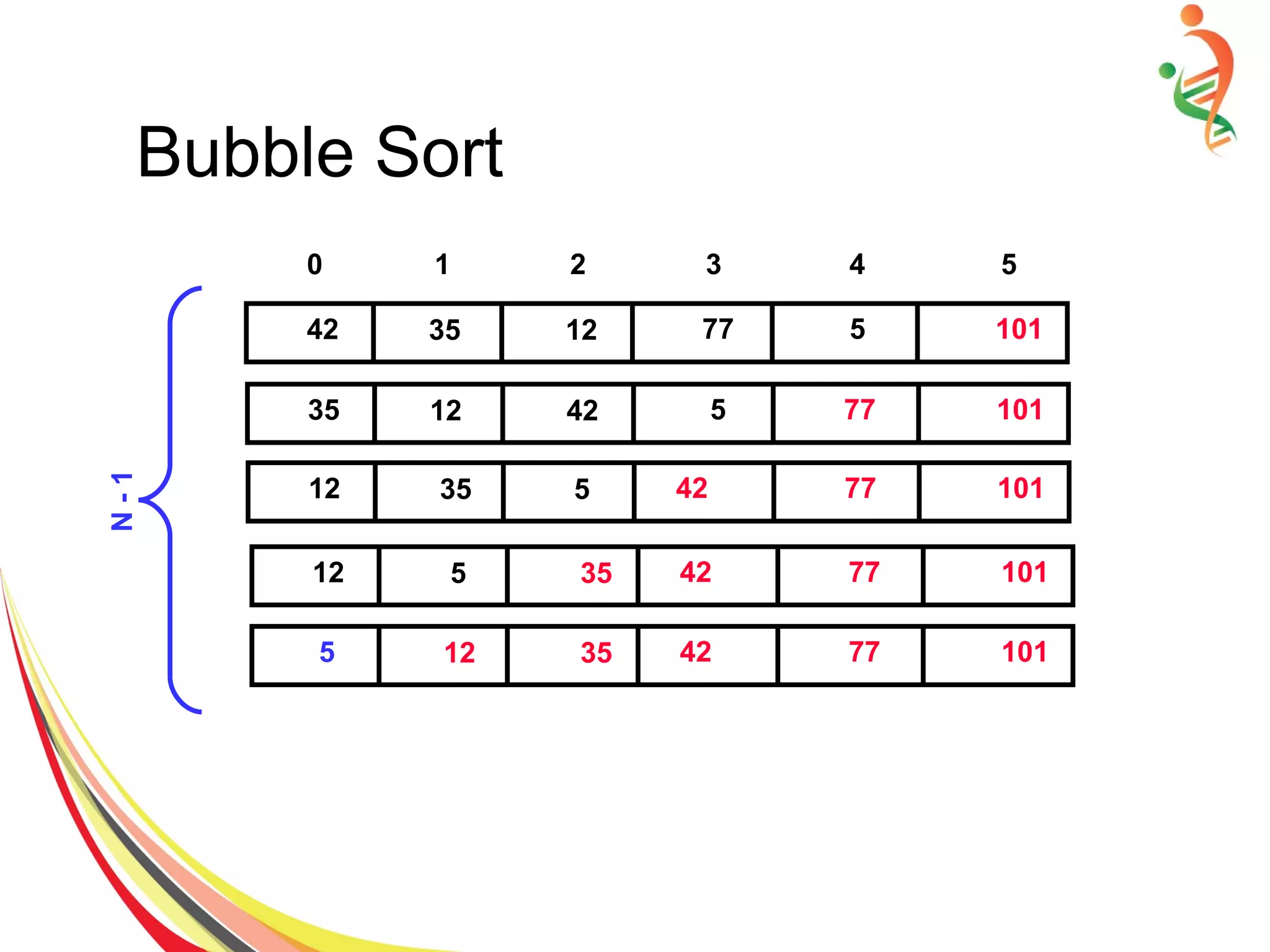
● Compare each pair of item and swap if required.
for(int pass=0; pass<n-1; pass ++)
for(int i=0; i<n-pass-1; i++)
If (item[ i ] > item [i+1]) {
tempvar = item[i]
Item[ i ] = item [i+1]
Item[ i+1]=tempvar
}
}
}

5. Bubble Sort
512354277 101
0 1 2 3 4 5
512354277 10142 77
512357742 10135 77
512773542 10112 77
577123542 101
77123542 5 101
Note: In phase 1 Largest element in the correct position
77 101

6. Bubble Sort
0 1 2 3 4 5
Note: In phase 2 Largest element place in the correct position
42 35 7712 5 101
42 12 77 5 10135
42 77 5 10135 12
77 5 10135 12 42
10135 12 42 5 77

7. Bubble Sort
0 1 2 3 4 5
10135 12 42 5 7735 12
10112 12 42 5 7735 42
10112 35 42 5 7742 5
10112 35 5 774212 35
10112 35 5 774235 5
10112 5 5 774235
1015 ●
12 5 774235125

8. Bubble Sort
77123542 5 101
5421235 77 101
4253512 77 101
4235512 77 101
4235125 77 101
N-1
0 1 2 3 4 5

9. Bubble Sort – Reducing Comparison
12354277 101 5
77123542 5 101
5421235 77 101
4253512 77 101
4235512 77 101
0 1 2 3 4 5

10. Analysis of Bubble Sort
● Works best when array is already nearly sorted
● Worst case number of comparisons is O(n2)
– e.g. input array values are 10,9,8,7,6,5,4,3,2,1
– On each step comparison required 9+8+7+... +1
– (n-1)*n /2
– O(n2)
● Best case occurs when the array is already sorted and
its complexity is O (n)
– input is in order (1,2,3,4,5,6,7,8,9,10)
– the algorithm still goes over each element once and
checks if a swap is necessary.

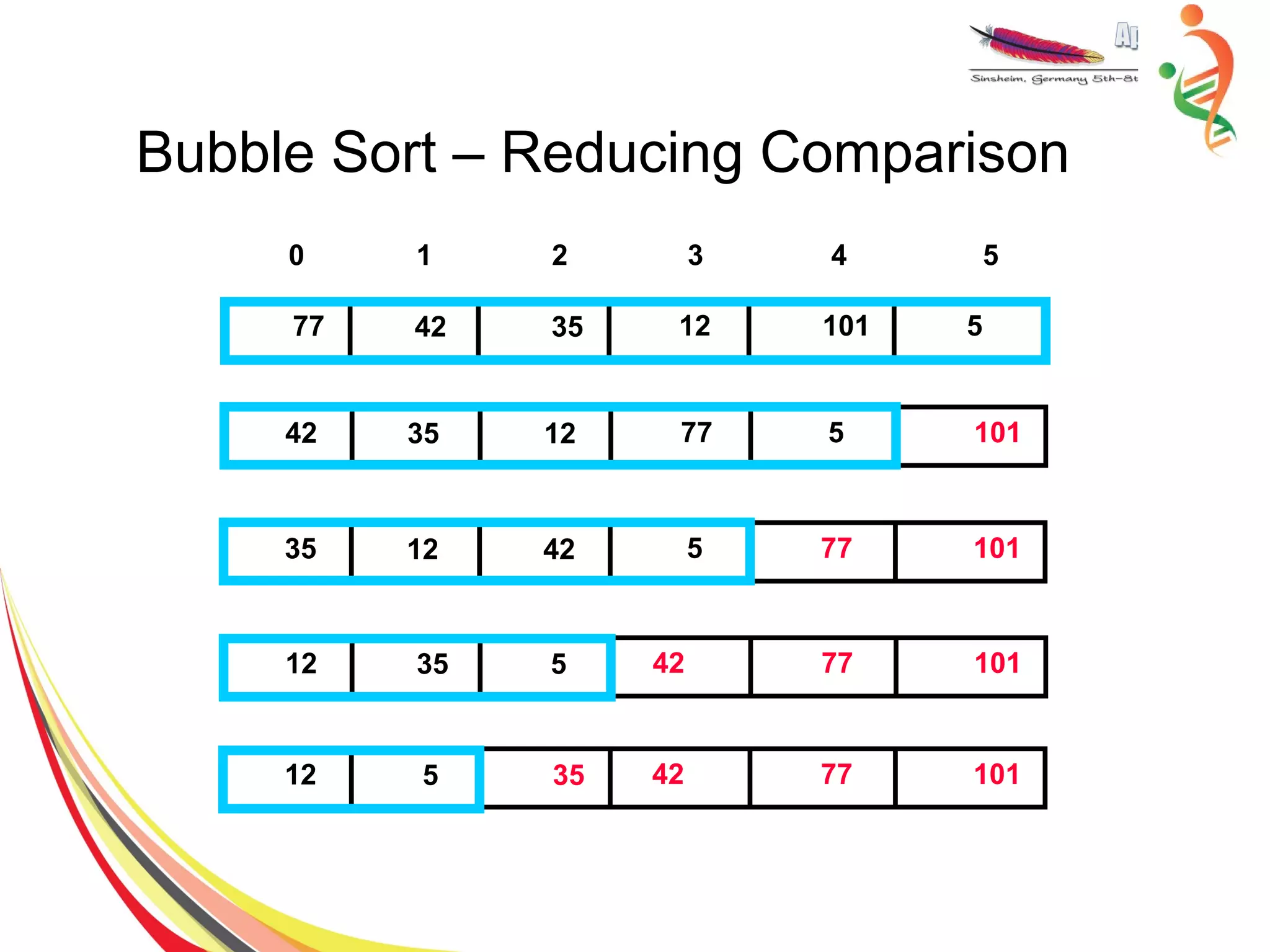
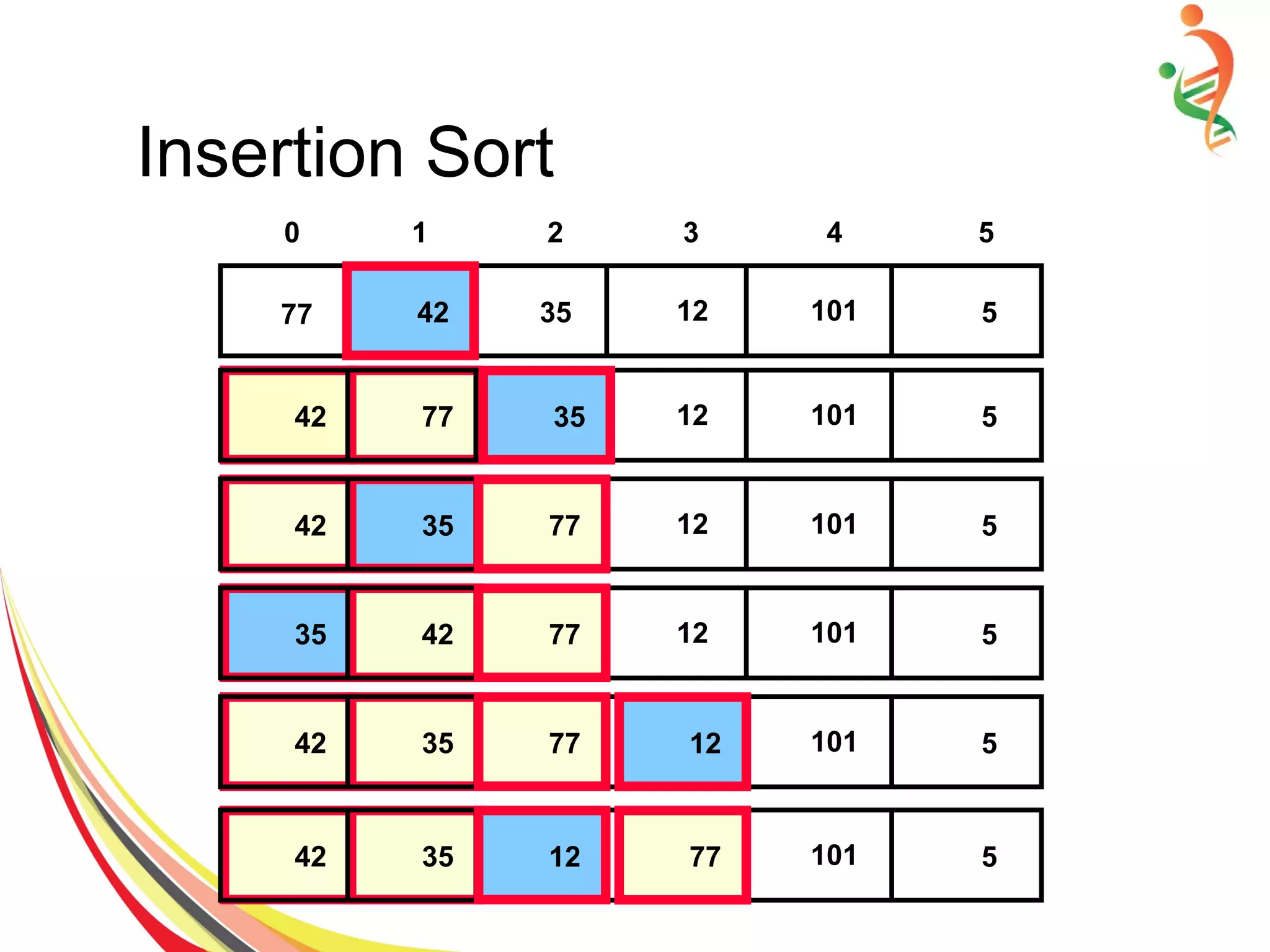
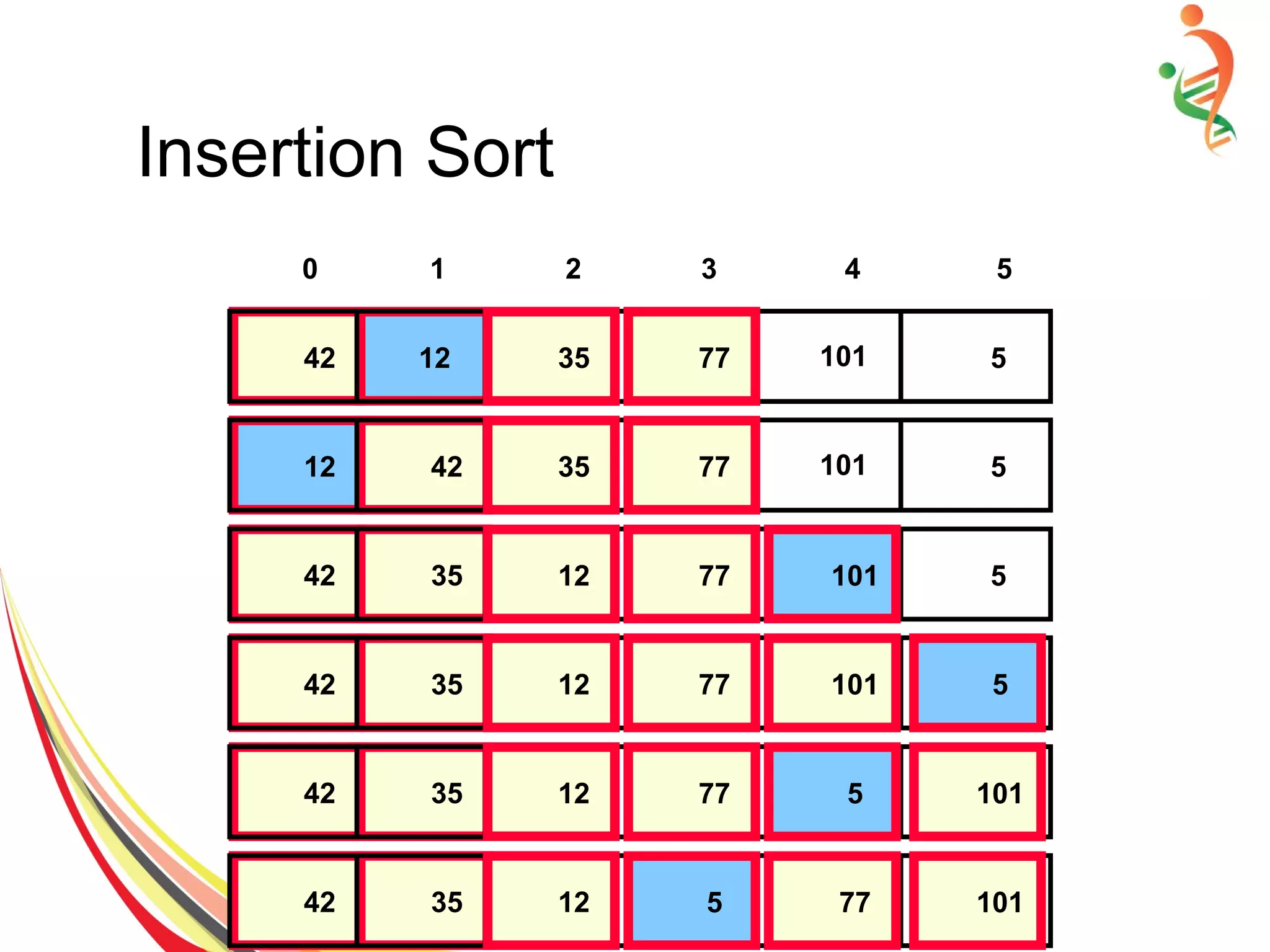
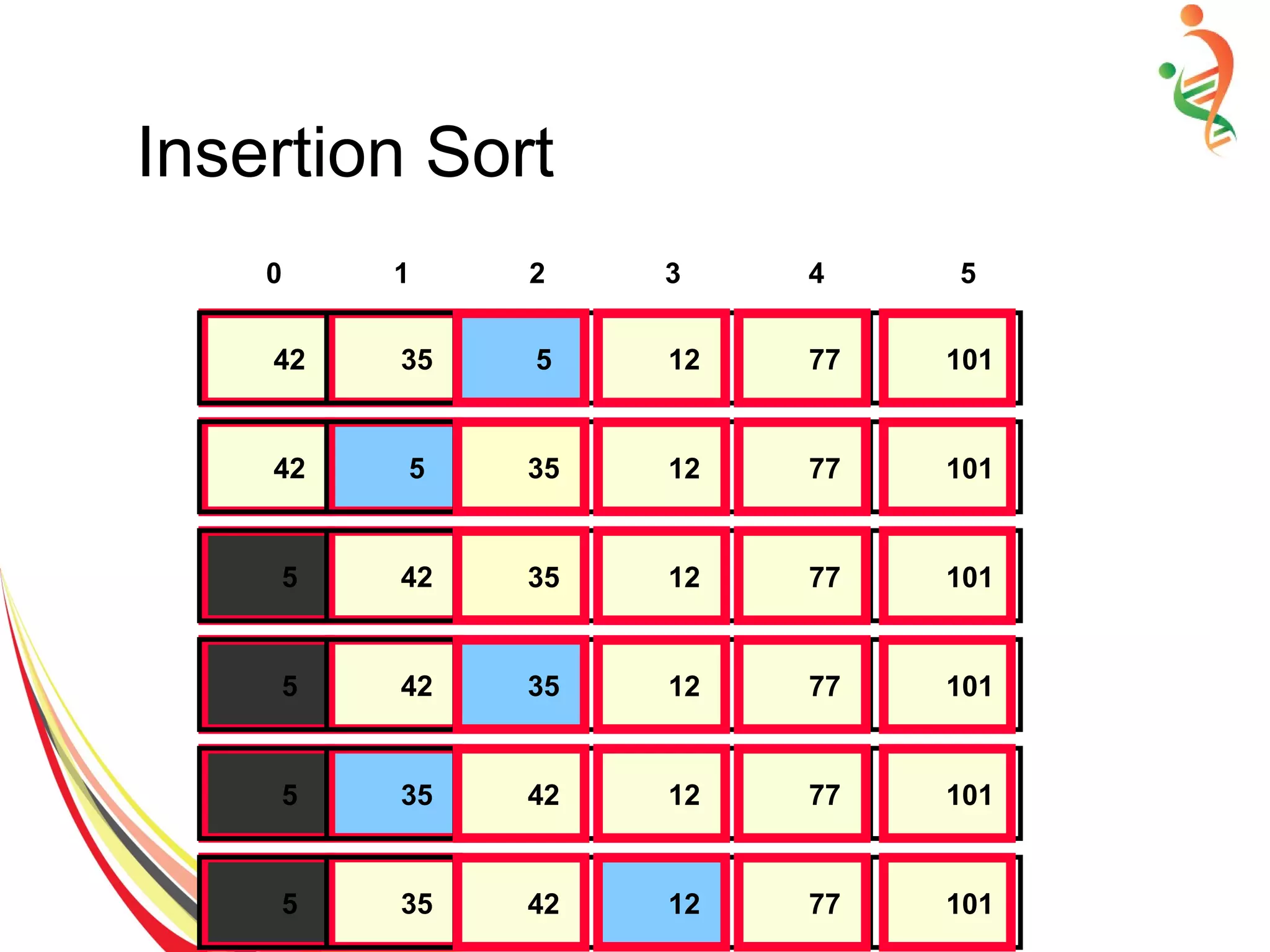
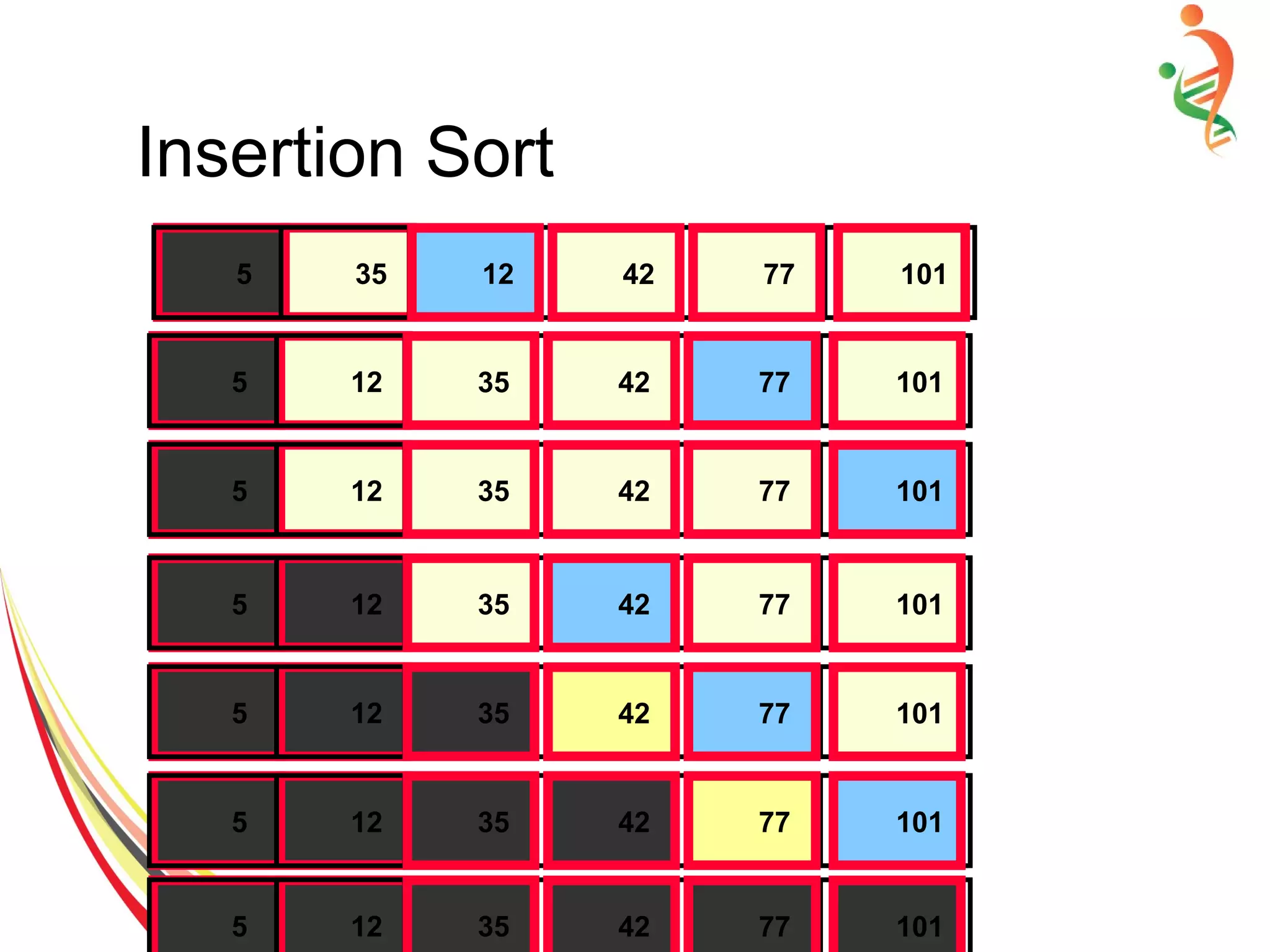
11. Insertion Sort
● Sort the elements in range[0,m] form = 0,...,n−1
● No action need form=0
● When going from m to m+1, insert the element
in index m+1, to its appropriate location

12. Algorithm of Insertion Sort
● This algorithm sorts the array a with n elements.
Set a[n] ={ 2,7,5,8,43,23..99}
● for (int i = 1; i < n; i++) //Array start from 0
{
Item tmp = a[i];
for (int j=i; j>0 && tmp < a[j-1]; j--)
a[j] = a[j-1];
a[j] = tmp;
}

13. Insertion Sort
512354277 101
42 77 51235 101
42 35 51235 10177
35 42 51235 10177
42 35 51235 10177 12
42 35 51235 10112 77
42
35
0 1 2 3 4 5

14. Insertion Sort
42 12 51235 10135 77
12 42 51235 10135 77
42 35 51235 10112 77 101
42 35 51235 10112 77 101 5
42 35 51235 10112 77 5 101
42 35 51235 10112 5 77 101
0 1 2 3 4 5

15. Insertion Sort
42 35 51235 1015 12 77 101
42 5 51235 10135 12 77 101
5 42 51235 10135 12 77 101
5 42 51235 10135 12 77 101
5 35 51235 10142 12 77 101
5 35 51235 10142 12 77 101
0 1 2 3 4 5

16. Insertion Sort
5 35 51235 10112 42 77 101
5 12 51235 10135 42 77 101
5 12 51235 10135 42 77 101
5 12 51235 10135 42 77 101
5 12 51235 10135 42 77 101
5 12 51235 10135 42 77 101
5 12 51235 10135 42 77 101

17. Selection Sort
● Find smallest element in the array and
exchange it with the element in the first
position.
● Find second smallest element and
exchange it with the element in the second
position
● Do this (n-1) times.
● Efficiency is O(n2)

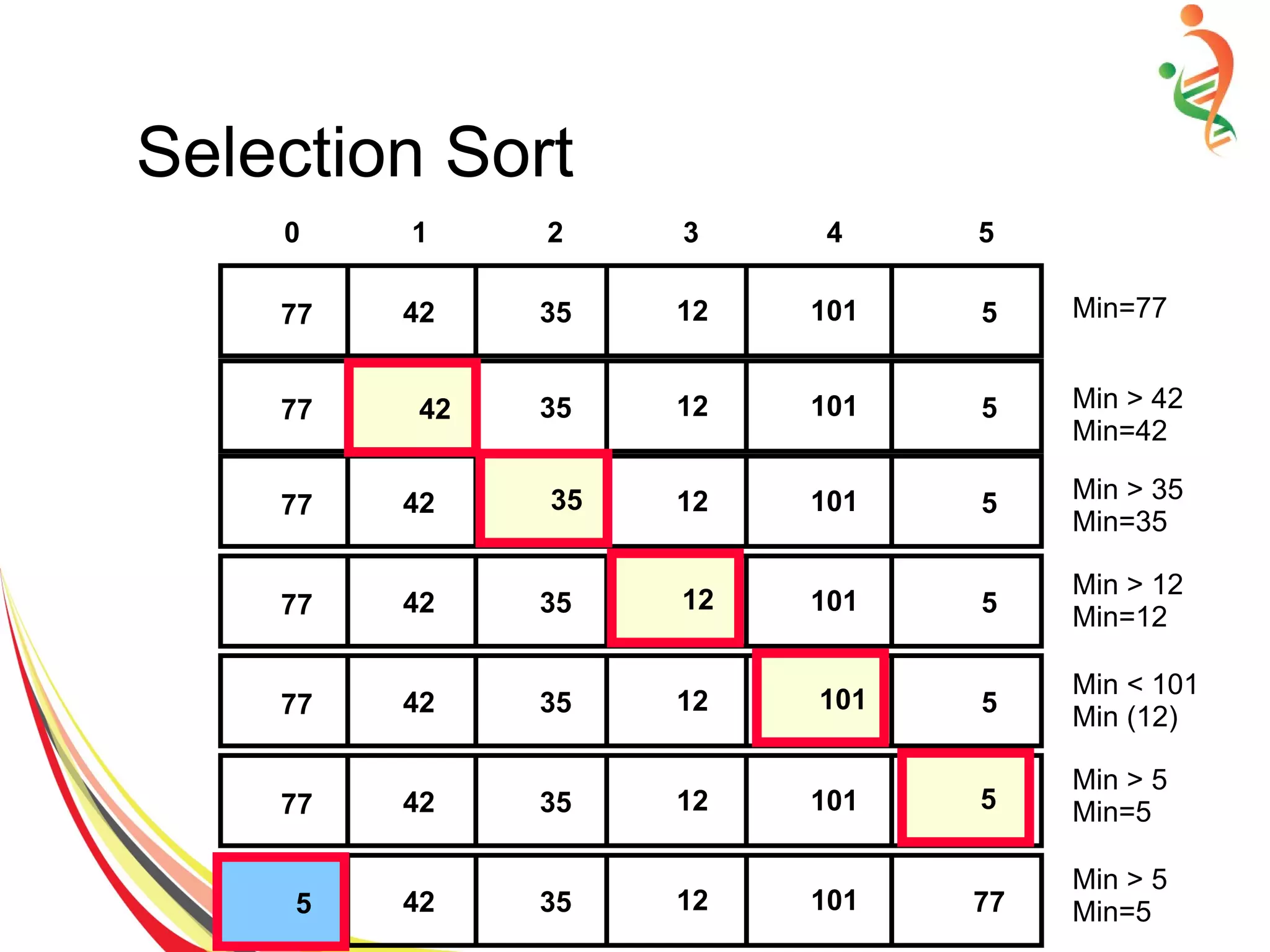
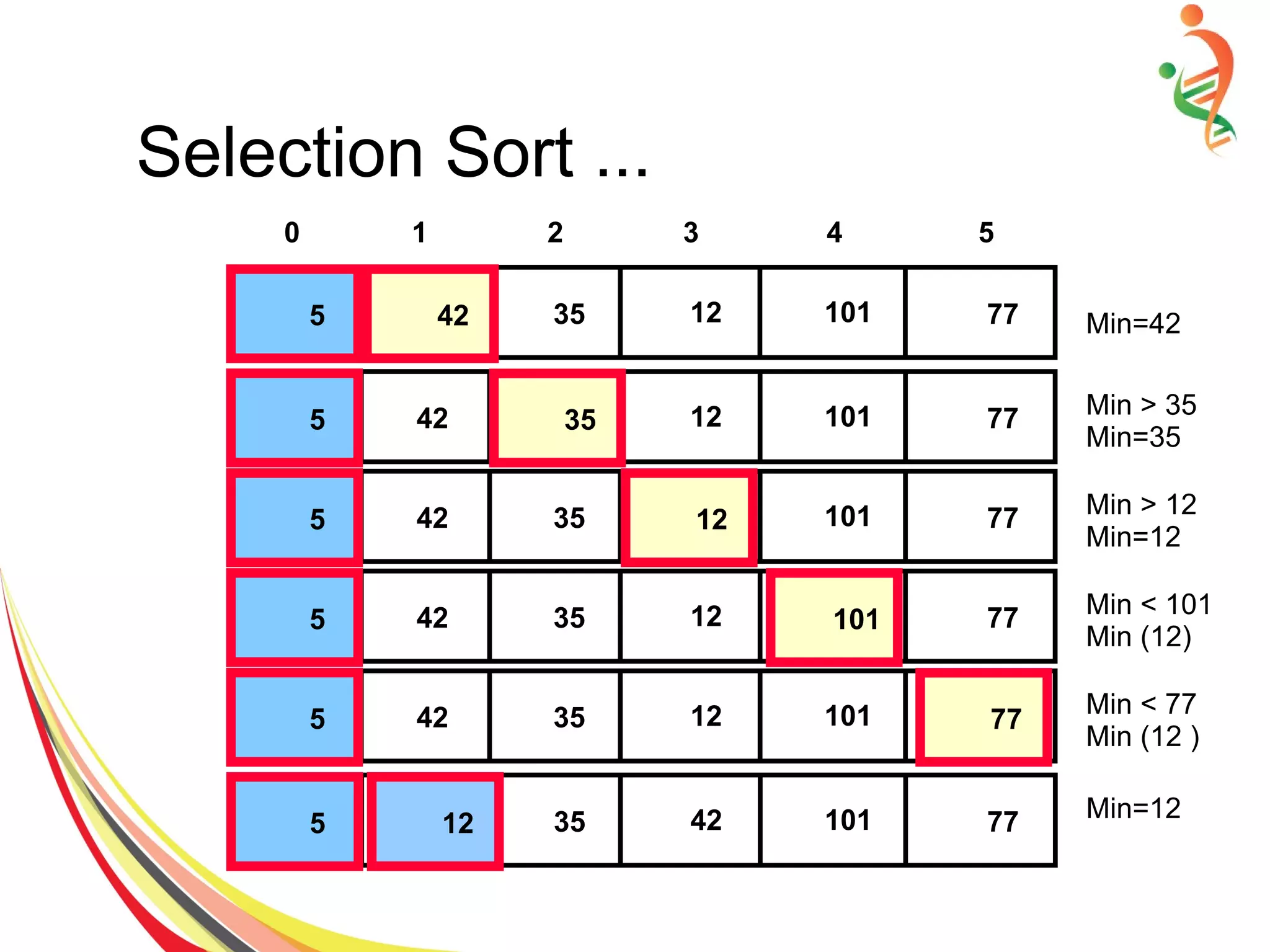
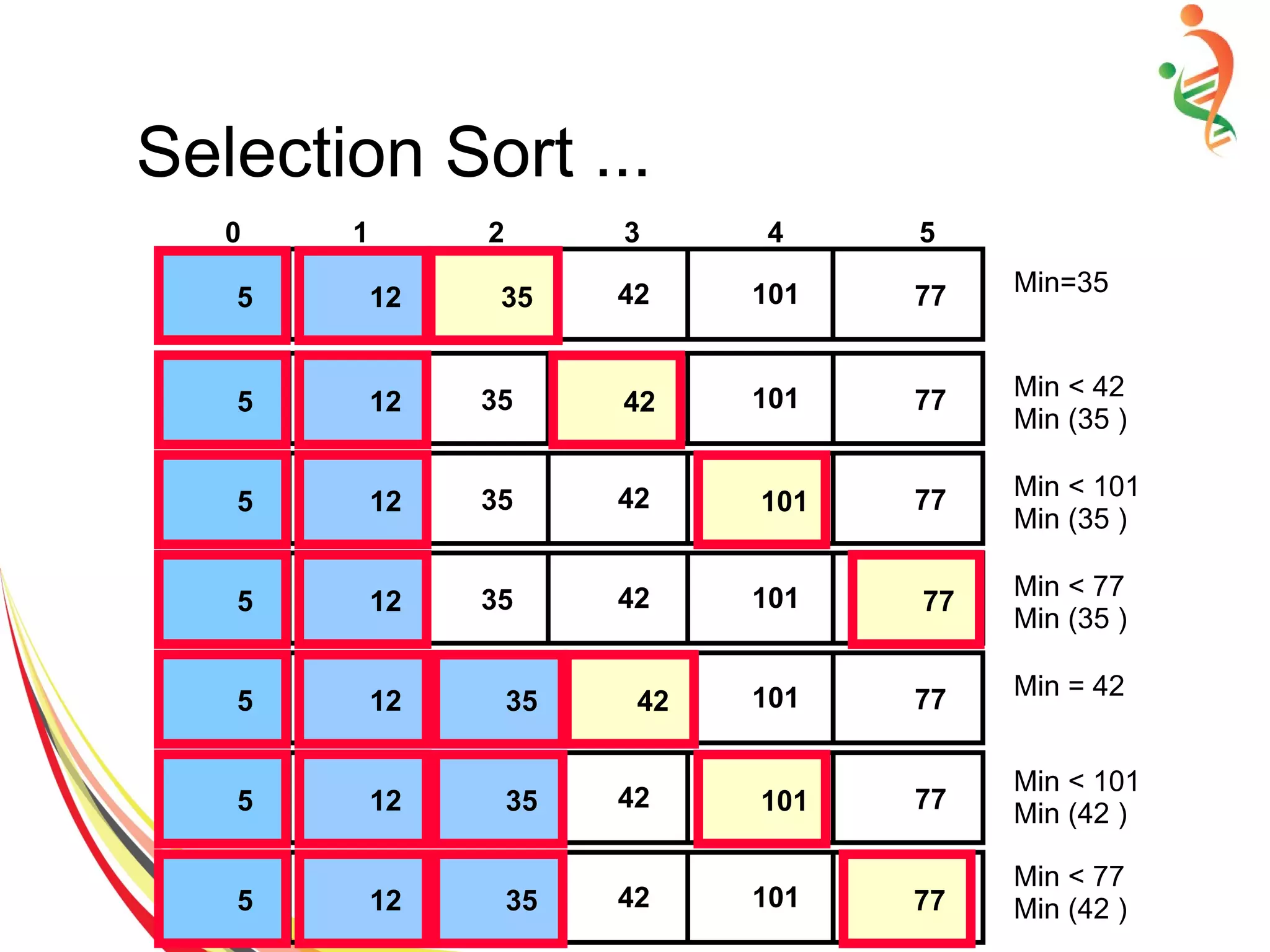
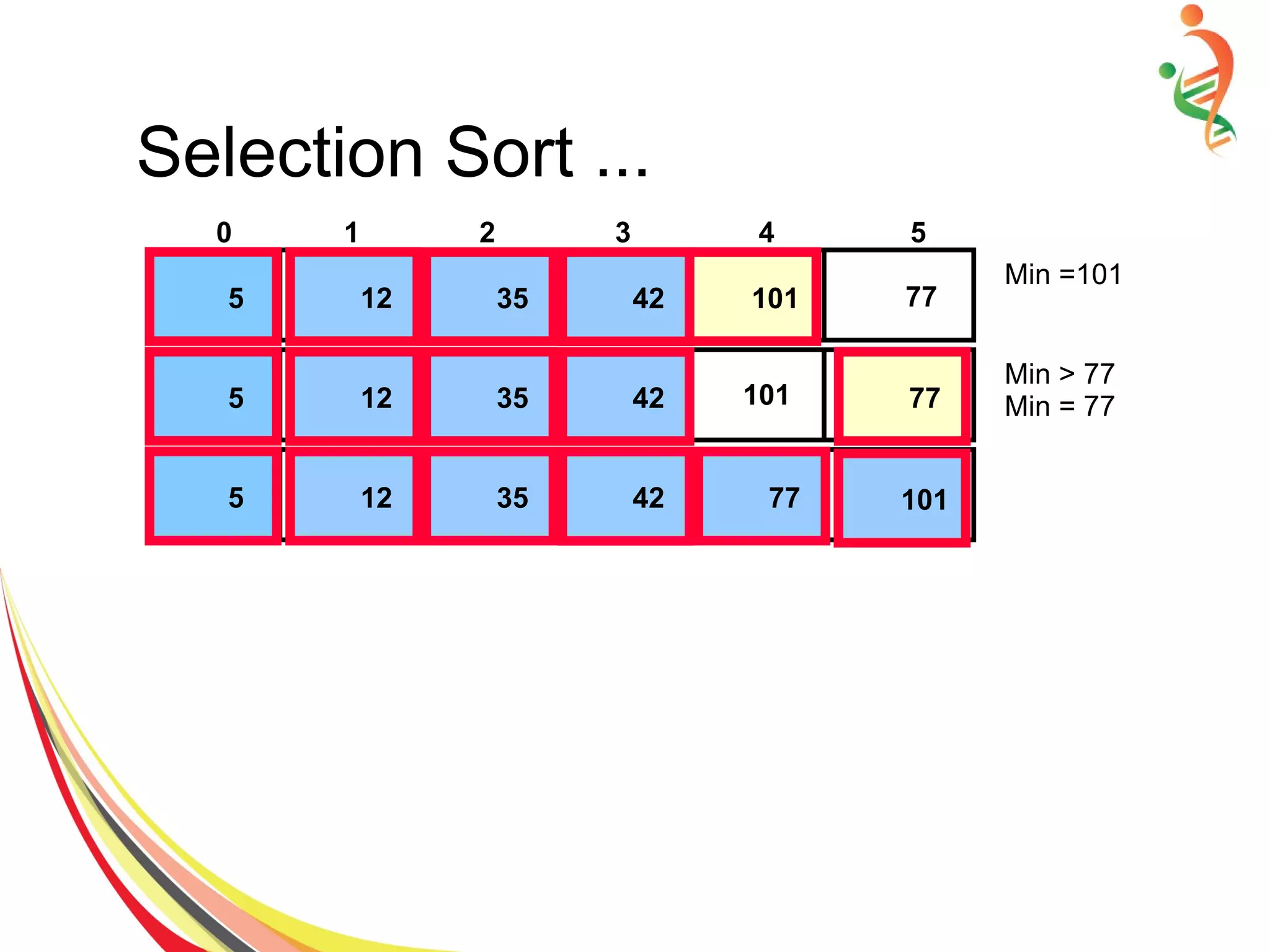
18. Selection Sort Algorithm
● Declare array on n items
Set items[n] = { 2,7,5,8,43,23..99}
● Find the min item and and iteratively swap with
first item if required.
for (int i = 0; i < n-1; i++) {
int min = i;
for (int j = i+1; j < n; j++)
if (a[j] < a[min]) min = j;
swap(a[i], a[min]);
}

19. Selection Sort
512354277 101 Min=77
512354277 101
512354277 101
42 Min > 42
Min=42
Min > 35
Min=35
35
512354277 10112
512354277 101101
512354277 101 5
Min > 12
Min=12
Min < 101
Min (12)
Min > 5
Min=5
771235425 1015
Min > 5
Min=5
0 1 2 3 4 5

20. Selection Sort ...
771235425 1015 Min=4242
771235425 1015 35
Min > 35
Min=35
771235425 1015 12
Min > 12
Min=12
771235425 1015 101
Min < 101
Min (12)
771235425 1015 77
Min < 77
Min (12 )
774235425 1015 12
Min=12
0 1 2 3 4 5

21. Selection Sort ...
774235425 1015 12
Min=35
35
774235425 1015 12
Min < 42
Min (35 )
42
774235425 1015 12
Min < 101
Min (35 )
101
774235425 1015 12
Min < 77
Min (35 )
77
774235425 1015 12
Min = 42
4235
774235425 1015 12 10135
774235425 1015 12 7735
Min < 101
Min (42 )
Min < 77
Min (42 )
0 1 2 3 4 5

22. Selection Sort ...
774235425 1015 12 10135
Min =101
42
774235425 1015 12 7735
Min > 77
Min = 7742
1014235425 1015 12 7735 42 101
0 1 2 3 4 5

23. Quick Sort
● The main concept of this sort is divide and
conquer
● Pick an element, say P (the pivot) Re-
arrange the elements into 3 sub-blocks,
● Repeat the process recursively for the left-
and right- sub-blocks.
● those less than or equal to (≤) P (the left-
block S1) P (the only element in the
middle-block)
● those greater than or equal to (≥) P (the
right- block S2)

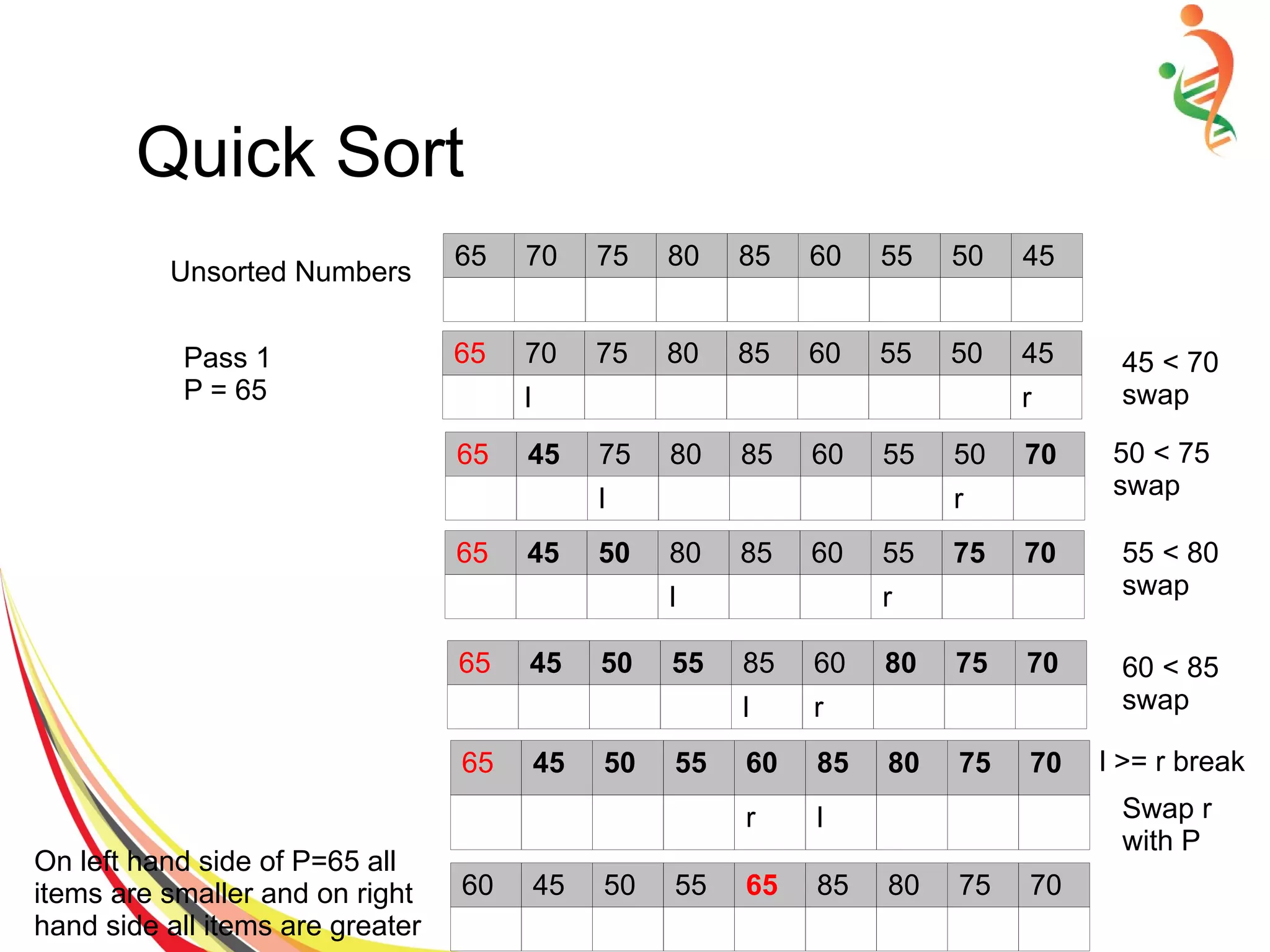
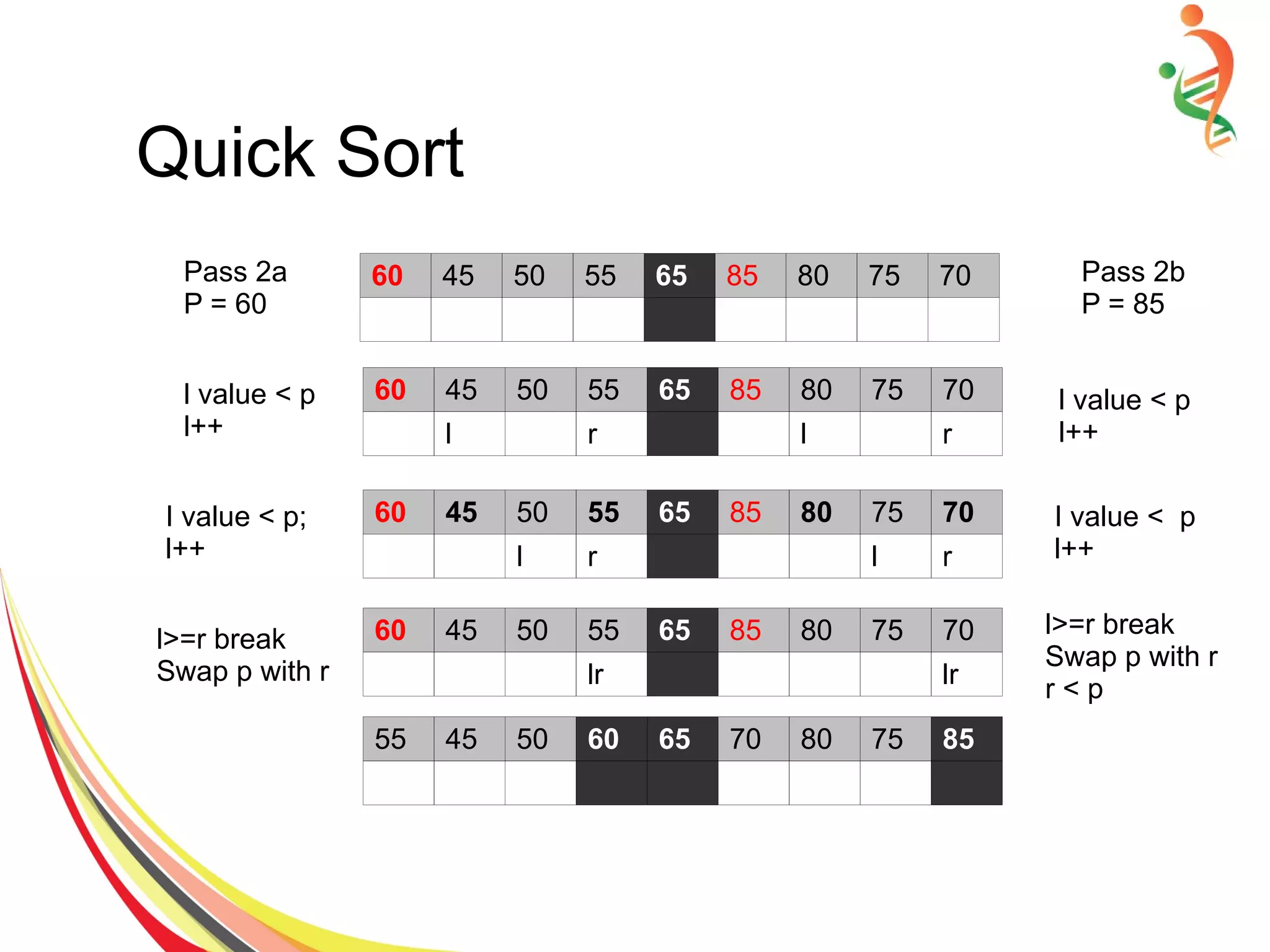
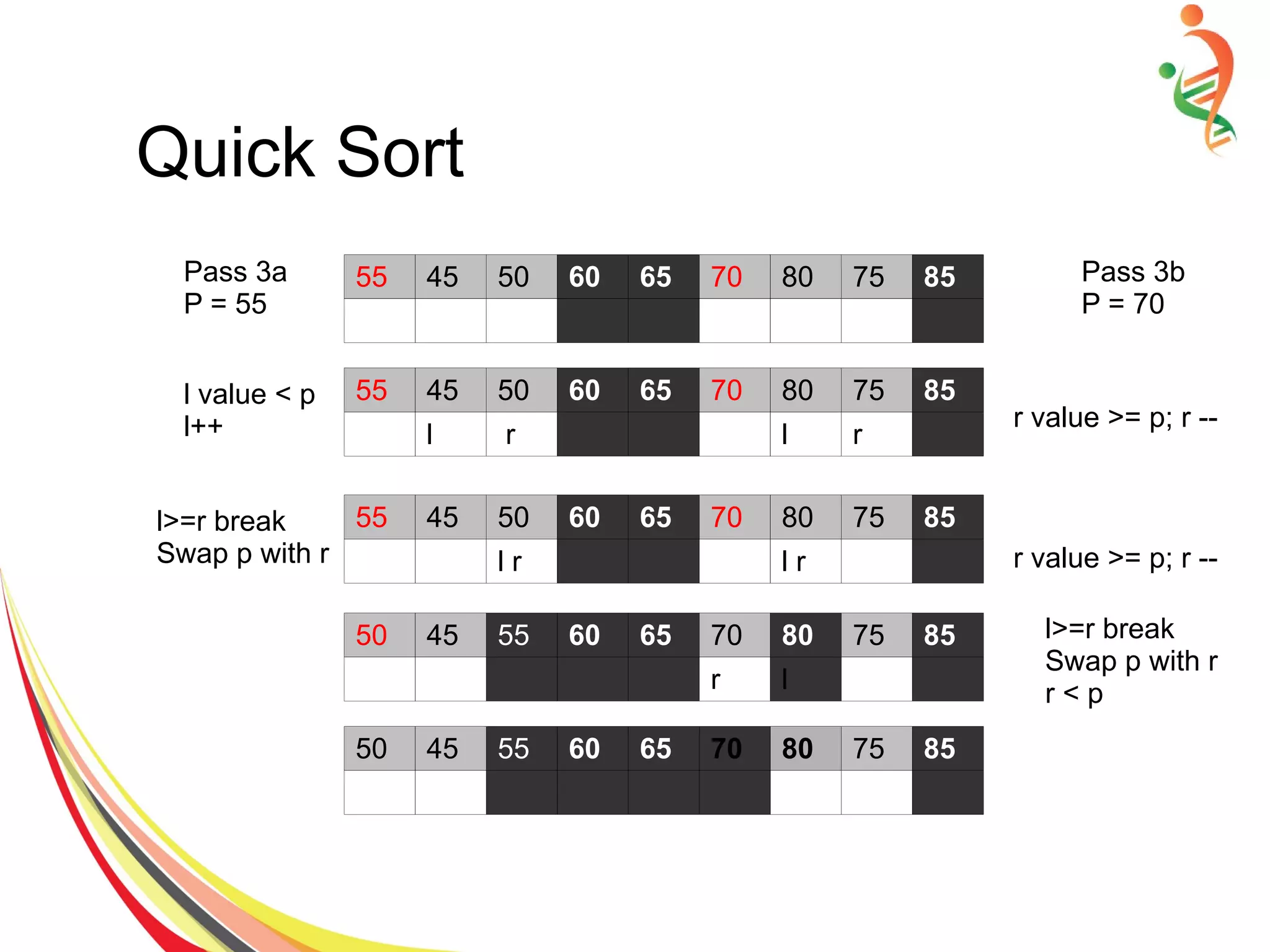
24. Quick Sort Algorithm
● Set pivot = a[left], l = left + 1, r = right;
● while l < r, do
– while l < right & a[l] < pivot , set l = l + 1
– while r > left & a[r] >= pivot , set r = r – 1
– if a[l] < a[r], swap a[l] and a[r]
● Set a[left] = a[r], a[r] = pivot
● Terminate

25. Quick Sort
65 70 75 80 85 60 55 50 45
Pass 1
P = 65
65 45 75 80 85 60 55 50 70
l r
65 45 50 80 85 60 55 75 70
l r
65 45 50 55 85 60 80 75 70
l r
65 45 50 55 60 85 80 75 70
r l
65 70 75 80 85 60 55 50 45
l r
Unsorted Numbers
45 < 70
swap
50 < 75
swap
55 < 80
swap
60 < 85
swap
l >= r break
Swap r
with P
60 45 50 55 65 85 80 75 70
On left hand side of P=65 all
items are smaller and on right
hand side all items are greater

26. Quick Sort
Pass 2a
P = 60
60 45 50 55 65 85 80 75 70 Pass 2b
P = 85
60 45 50 55 65 85 80 75 70
l r l r
l value < p
l++
l value < p
l++
60 45 50 55 65 85 80 75 70
l r l r
I value < p
l++
I value < p;
l++
l>=r break
Swap p with r
l>=r break
Swap p with r
r < p
60 45 50 55 65 85 80 75 70
lr lr
55 45 50 60 65 70 80 75 85

27. Quick Sort
Pass 3a
P = 55
Pass 3b
P = 70
l value < p
l++ r value >= p; r --
l>=r break
Swap p with r
l>=r break
Swap p with r
r < p
55 45 50 60 65 70 80 75 85
55 45 50 60 65 70 80 75 85
l r l r
55 45 50 60 65 70 80 75 85
l r l r
50 45 55 60 65 70 80 75 85
r l
50 45 55 60 65 70 80 75 85
r value >= p; r --

28. Quick Sort
Pass 4a
P = 50
Pass 4b
P = 80
l value < p
l++ l value < p; l ++
l>=r break
Swap p with r
l>=r break
Swap p with r
r < p
50 45 55 60 65 70 80 75 85
l r l r
50 45 55 60 65 70 80 75 85
r l r l
45 50 55 60 65 70 75 80 85
r l r i
45 50 55 60 65 70 75 80 85
Sorted

29. Sorting Complicity Table
Sorting Algorithm Worst Case Best Case Average Case
Bubble Sort O(n^2) O(n) O(n^2)
Insertion Sort O(n^2) O(n) O(n^2)
Selection Sort O(n^2) O(n^2) O(n^2)
Quick Sort O(n^2) O(n log(n)) O(n log(n))

30. Sorting Algorithm Animations
● http://www.ee.ryerson.ca/~courses/coe428/
sorting/insertionsort.html

31. Sequential Search
● Search key is compared with all elements
in the list,
● O(n) time consuming for large datasets
● Time can reduced if data is sorted.

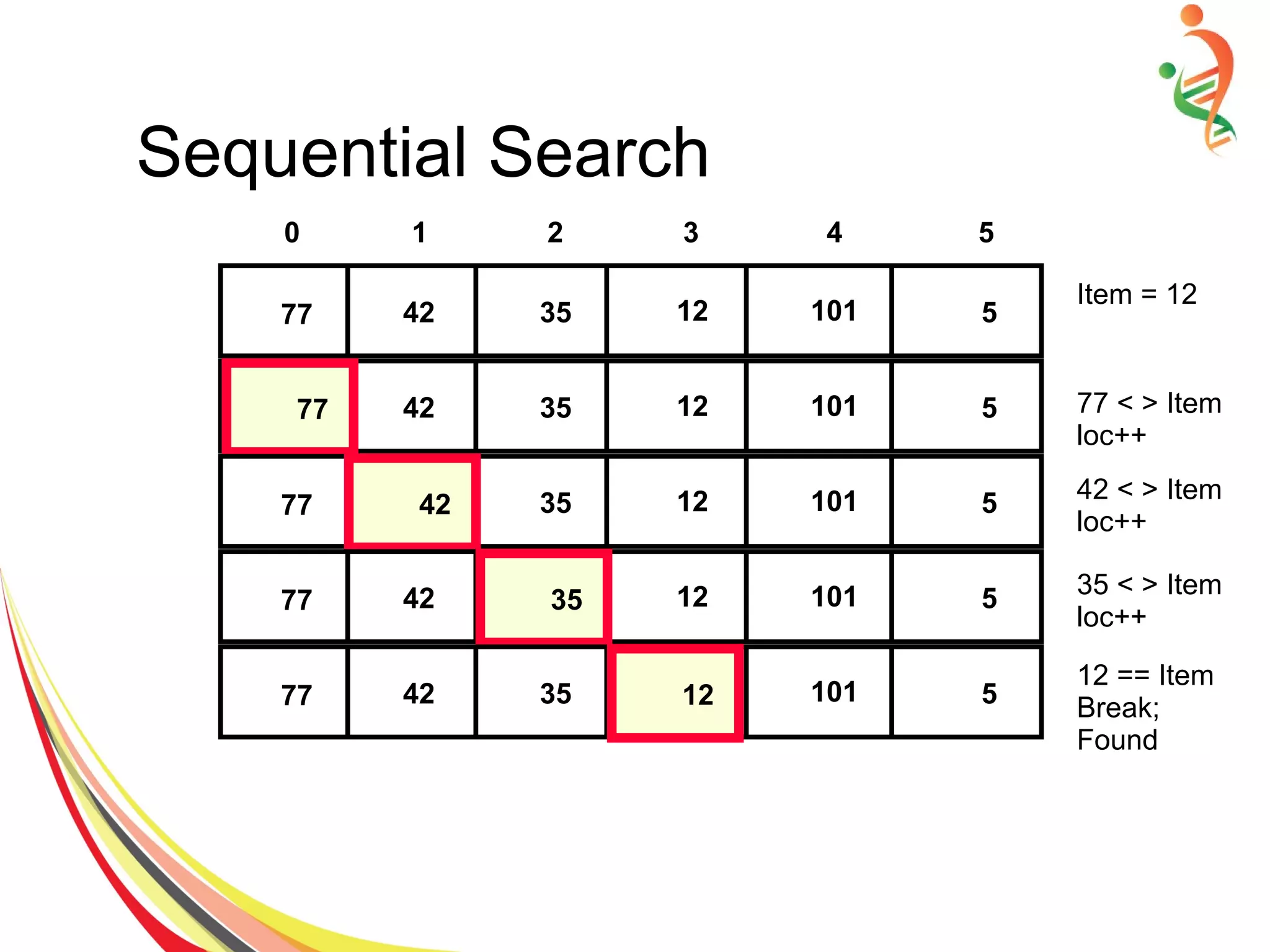
32. Sequential Search Algorithm
● Declare array on n items
Set items[n] = { 2,7,5,8,43,23..99}
● Find a number into provided items array.
bool found = false;
for(int loc = 0; loc < n; loc++)
if(items[loc] == item) {
found = true;
break; }
if(found)
return loc;
else
return -1;

33. Sequential Search
512354277 101
0 1 2 3 4 5
Item = 12
512354277 10177 77 < > Item
loc++
512354277 10142
42 < > Item
loc++
512354277 10135
35 < > Item
loc++
512354277 10112
12 == Item
Break;
Found

34. Binary Search
● Use divide and conquer technique to search item.
● Complexity of binary search is O(log n)
● Can only be performed on sorted list.
● Searching criteria:
– Search item is compared with middle element of list.
– If search item < middle element of list, search is
restricted to first half of the list.
– If search item > middle element of list, search second
half of the list.
– If search item = middle element, search is complete.

35. Binary Search Algorithm
● Declare array of n items
Set items[n] = { 2,7,5,8,43,23..99}
● Find a number into provided items
array.
● int first = 0; int mid; int last=n -1
● bool found = false;
● while(first <= last && !found) {
– mid = (first + last) / 2 ;
– if(items[mid] ==item)
found=true;
else
if(items[mid] > item)
last=mid-1;
else
first= mid+1;
}
if(found)
return mid;
else
return -1;

36. Binary Search
1021225102 101
0 1 2 3 4 5 6
110
First =0; Last = 6; Mid=(0+6)/2=3
Item= 101
Items[3]<>10145
1024525102 101 110102
items[mid]< 101; First=4; Last=6; Mid=(4+6)/2=5
Items[5]<>101
1024525102 101 110101
items[mid]> 101; First=4; Last=4; Mid=(4+4)/2=4
Items[4]==101
Found