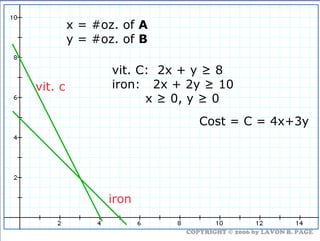
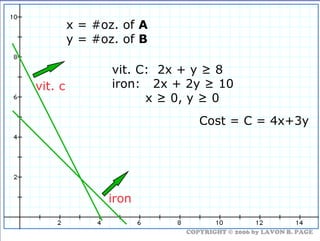
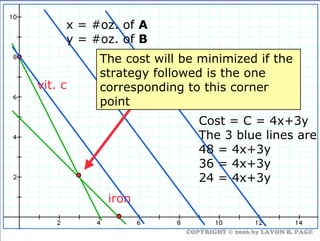
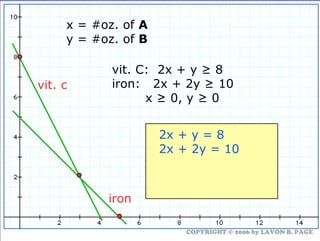
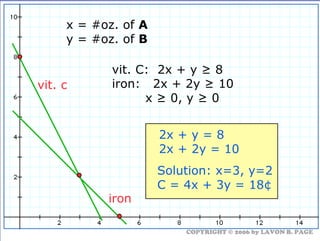
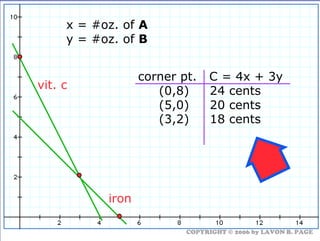
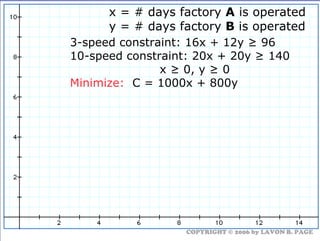
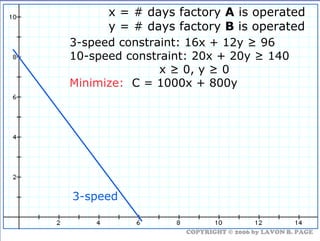
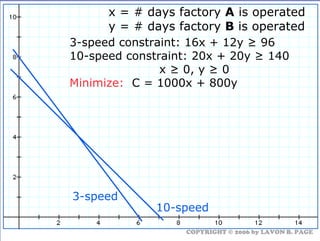
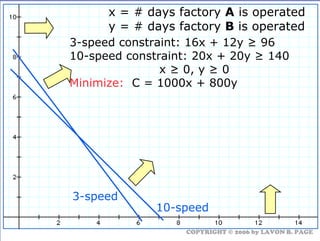
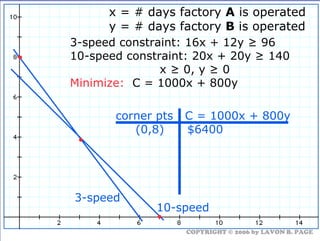
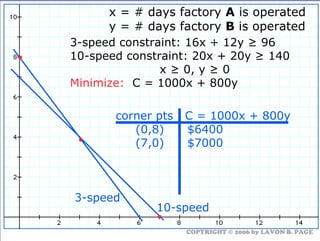
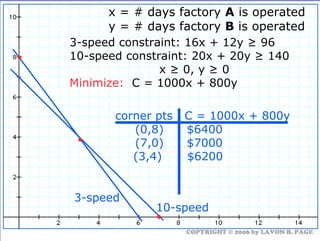
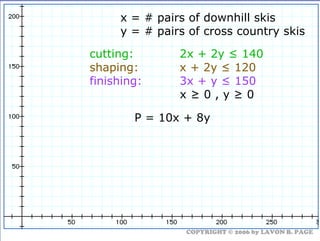
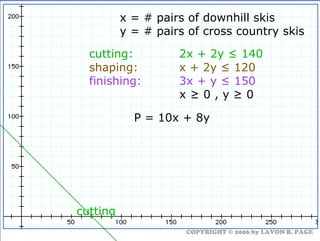
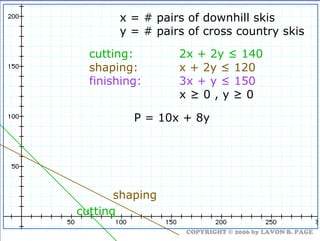
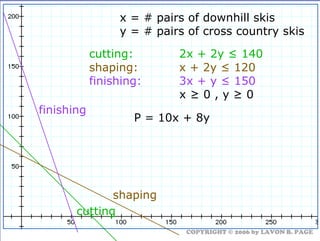
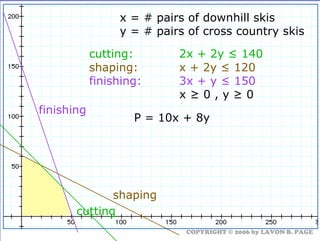
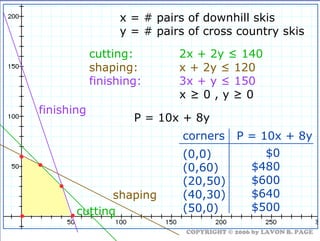
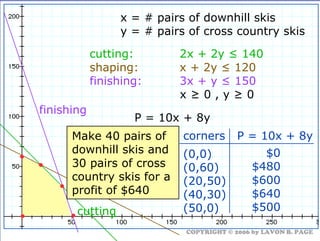
The document discusses using linear programming to solve optimization problems graphically. It provides examples of using the graphical method to determine the optimal mix of food items in a diet and production levels at bicycle factories to minimize costs. The examples show setting up the objective function and constraints, plotting them graphically, and finding the corner point that maximizes profit or minimizes costs. The optimal solutions for the examples are also presented.