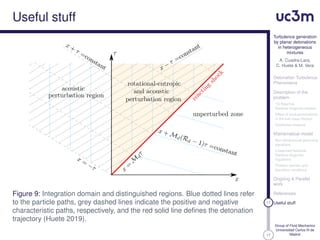
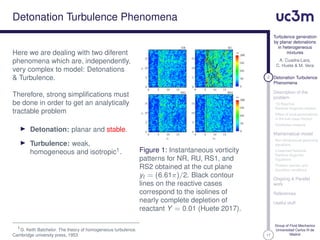
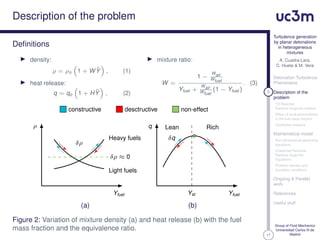
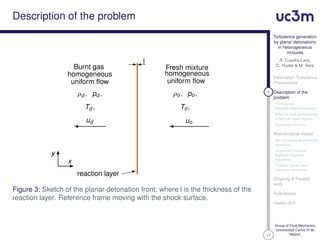
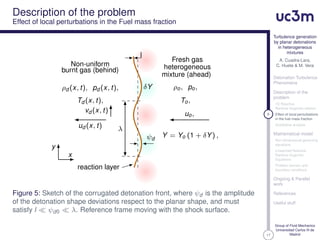
This document presents research on turbulence generation by planar detonations in heterogeneous fuel-air mixtures. The authors describe their mathematical model which uses the linearized reactive Rankine-Hugoniot equations to analyze how local perturbations in the fuel mass fraction affect the detonation front shape and generate turbulence. They discuss assumptions made, the governing non-dimensional equations, and the problem domain and boundary conditions considered in their ongoing work.
















![17
Turbulence generation
by planar detonations
in heterogeneous
mixtures
A. Cuadra-Lara,
C. Huete & M. Vera
Detonation Turbulence
Phenomena
Description of the
problem
1D Reactive
Rankine-Hugoniot relation
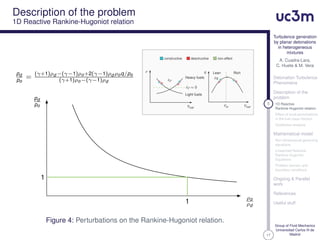
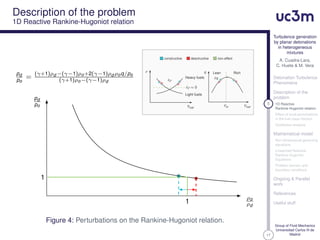
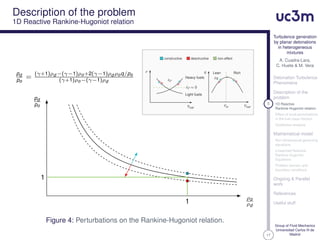
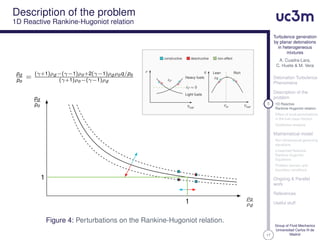
Effect of local perturbations
in the fuel mass fraction
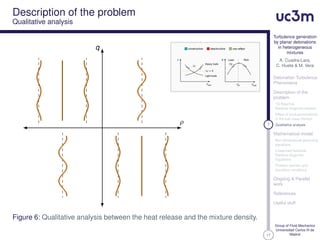
Qualitative analysis
Mathematical model
Non-dimensional governing
equations
Linearized Reactive
Rankine-Hugoniot
Equations
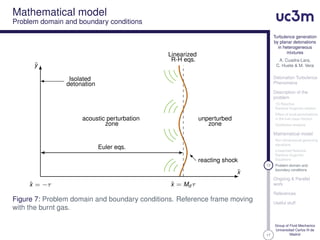
Problem domain and
boundary conditions
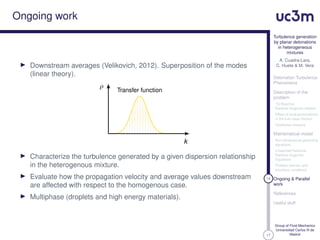
15 Ongoing & Parallel
work
References
Useful stuff
Group of Fluid Mechanics
Universidad Carlos III de
Madrid
Parallel work
Development and validation of a new
MATLAB R
/GUI based thermochemi-
cal code, A. Cuadra-Lara & M. Vera.
Figure 8: Current state of the GUI
Combustion-Toolbox developed.
0.5 1 1.5 2 2.5 3 3.5 4 4.5
10
-15
10
-10
10
-5
10
0
Figure 4: Variation of molar fraction with equivalence ra-
tio for lean to rich acetylene-air mixtures. Combustion-
Toolbox (line) and CEA (diamond).
Development and validation of a new
MATLAB/GUI based thermochemical code
Alberto Cuadra-Lara & Marcos Vera
Department of Thermal and Fluids Engineering, University Carlos III of Madrid
acuadra@ing.uc3m.es (ACL), marcos.vera@uc3m.es (MV)
MSC11, 11th Mediterranean Combustion Symposium
Tenerife, Spain | Jun 16-20 2019
Motivation
In a wide range of applications involving chemically reacting flows, thermochemical
calculations involving overall mass and energy balances with chemical equilibrium
are enough to estimate the overall performance of the system. This is often deter-
mined by magnitudes such as the adiabatic flame temperature or the equilibrium
composition of the products. Thermochemical codes have been developed for this
purpose dating back to the late 1940’s at the NACA Lewis Flight Propulsion Labo-
ratory, with the initial aim of evaluating rocket performance of various potential pro-
pellants. The use of thermochemical codes has been growing ever since, and today
they are basic research tools both for combustion applications and in the analysis of
the thermal decomposition of high-energy materials (HEMs), including deflagration
and detonation conditions.
Introduction
As a first step towards the development of a wider-scope thermochemical tool, in this
work we present a thermochemical code with application to gaseous combustion
problems recently implemented by the authors in MATLAB R
. The code solves six
chemical equilibrium problems (TP, HP, SP, TV, EV and SV transformations; where
T denotes temperature, P pressure, H enthalpy, S entropy, E internal energy and
V volume), incident and reflected planar shock waves, as well as ideal detonations
according to Chapman-Jouguet theory, assuming always ideal gases in all cases.
The code computes the equilibrium composition using equilibrium constants rather
than by minimization of the Gibbs–Helmholtz free energy, and employs NASA’s
9-coefficient polynomial fits to evaluate the thermodynamic properties. Along with
the plain code, the new tool has been equipped with a Graphical User Interface
(hereafter Combustion-Toolbox) developed in MATLAB R
2018 under AppDe-
signer.
Results computed with Combustion-Toolbox have been validated against, and are
in good agreement with, NASA’s Chemical Equilibrium with Applications (CEA) pro-
gram [1], CANTERA, and Caltech’s Shock and Detonation Toolbox [2]. Moreover,
the time required for the computations is comparable to that of other existing codes.
Combustion-Toolbox has teaching and research aspirations and will be distributed
as open source package as soon as it has been fully tested.
Combustion-Toolbox
Available thermochemical transformations
1. TP: equilibrium composition at defined temperature and pressure.
2. HP: adiabatic temperature and composition at constant pressure.
3. SP: isentropic compression/expansion to a specified pressure.
4. TV: equilibrium composition at defined temperature and constant volume.
5. EV: adiabatic temperature and composition at constant volume.
6. SV: isentropic compression/expansion to a specified volume.
7. SHOCK I: planar incident shock wave at normal incidence.
8. SHOCK R: planar reflected shock wave at normal incidence.
9. DET: Chapman-Jouget detonation (CJ upper state).
Database
• Employs 9-coefficient polynomial fits to evaluate the thermodynamic properties
from NASA’s thermodynamic database (2075 species) [3].
Features
• The reactant mixture is specified by fuel-air mixture, equivalence ratio, and/or the
number of moles (or mole fraction) of the different species, which can also have
different temperature.
• Parametric sweeps for different input parameters, such as the equivalence ratio φ.
• Solves both complete and incomplete (i.e., dissociation) combustion problems.
For incomplete combustion, the minor species present in the final equilibrium can
be selected at will, with some preselected subsets already defined.
• The equilibrium composition can be solved considering condensed species
(graphite so far).
• Can estimate thermal NOx for a given residence time.
• Automatic plots of the product composition and thermodynamic properties as a
function of the equivalence ratio φ.
• Detailed results reported via the MATLAB R
command window or an Excel file.
• Personalized use and modification of the plain code and routines.
• Easy access to all the results of a working session through an editable tree dia-
gram.
Algorithms
• The equilibrium composition is computed using an iterative segregated solver that
estimates first the minor species from suitable (nonlinear) equilibrium conditions
and then corrects the major species to guarantee (linear) atom conservation.
• The thermochemical transformations HP, SP, EV, and SV are computed using a
Steffensen-Aitken root-finding algorithm which employs the iterative segregated
solver.
• Incident and reflected planar shock waves, as well as ideal detonations according
to Chapman-Jouget theory, are computed using a Newton-Raphson root-finding
algorithm as [4]. It also employs the iterative segregated solver.
Figure 2: Current state of the GUI Combustion-Toolbox developed.
Results
In order to validate the model, Figure 3 shows the adiabatic
flame temperature for different fuel-air mixtures initially at
room temperature and pressure. Figure 4 shows the vari-
ation of the molar fraction of the product species with the
equivalence ratio for lean to rich acetylene-air mixtures, with
φgr =
2
x − z
x +
y
4
−
z
2
, (1)
the theoretical starting value for soot formation, and x, y, z
the number of moles of carbon, hydrogen and oxygen in the
fuel molecule, respectively. Figure 5 shows some results
(density, detonation velocity, temperature and pressure), ob-
tained from a Chapman-Jouget detonation of a ethylene-air
mixture.
All the results are in good agreement with NASA’s Chemi-
cal Equilibrium with Applications (CEA) program, CANTERA,
and Caltech’s Shock and Detonation Toolbox.
0.5 1 1.5 2 2.5 3 3.5 4 4.5
1400
1600
1800
2000
2200
2400
2600
2800
C2H2
C6H6
Lean Rich Rich-Sooting
Figure 3: Adiabatic flame temperature as a function of the
equivalence ratio for different fuel-air mixtures: acetylene
(C2H2), and benzene (C6H6). Combustion-Toolbox (line) and
CEA (diamond).
0.6 0.8 1 1.2 1.4 1.6 1.8
2
2.05
2.1
0.6 0.8 1 1.2 1.4 1.6 1.8
2
2.02
2.04
2.06
2.08
2.1
(a)
0.5 1 1.5
1500
1600
1700
1800
1900
(b)
0.5 1 1.5
2000
2200
2400
2600
2800
3000
(c)
0.6 0.8 1 1.2 1.4 1.6 1.8
12
14
16
18
20
(d)
Figure 5: Chapman-Jouget det-
onation properties for an ethylene-
air mixture initially at room tempera-
ture and pressure as a function of
the equivalence ratio: (a) density,
(b) detonation velocity, (c) tempera-
ture, (d) pressure. Results validated
with CEA (NASA) and CANTERA
with Caltech’s Shock and Detona-
tion Toolbox.
References
[1] F. J. Zeleznik and S. Gordon. Calculation of complex chemical equilibria. Industrial & Engineering Chemistry,
60 (6):27–57, 1968.
[2] S. Browne, J. Ziegler and J. E. Shepherd Shock and Detonation Toolbox. GALCIT-Explosion Dynamics
Laboratory, Pasadena, CA, 2008.
[3] B. J. McBride, M. J. Zehe and S. Gordon. NASA Glenn coefficients for calculating thermodynamic properties
of individual species, 2002.
[4] S. Browne, J. Ziegler and J. E. Shepherd. Numerical solution methods for shock and detonation jump
conditions. Energy Conservation, 1 (w2), 2004.](https://image.slidesharecdn.com/wfmacuadra-200928202543/85/Slides-Workshop-on-Fluid-Dynamics-2019-28-320.jpg)
![17
Turbulence generation
by planar detonations
in heterogeneous
mixtures
A. Cuadra-Lara,
C. Huete & M. Vera
Detonation Turbulence
Phenomena
Description of the
problem
1D Reactive
Rankine-Hugoniot relation
Effect of local perturbations
in the fuel mass fraction
Qualitative analysis
Mathematical model
Non-dimensional governing
equations
Linearized Reactive
Rankine-Hugoniot
Equations
Problem domain and
boundary conditions
Ongoing & Parallel
work
16 References
Useful stuff
Group of Fluid Mechanics
Universidad Carlos III de
Madrid
References
[1] Lee, J. The Detonation Phenomenon. Cambridge University Press (2008).
[2] Kailasanath, K. Review of propulsion applications of detonation waves.
AIAA journal 38.9 (2000): 1698-1708.
[3] Veyssiere, B., and B. A. Khasainov. Structure and multiplicity of detonation
regimes in heterogeneous hybrid mixtures. Shock Waves 4.4 (1995):
171-186.
[4] Kailasanath, K. Liquid-fueled detonations in tubes. Journal of Propulsion
and Power 22.6 (2006): 1261-1268.
[5] Watanabe, Hiroaki, et al. Numerical investigation on propagation behavior
of gaseous detonation in water spray. Proceedings of the Combustion
Institute 37.3 (2019): 3617-3626.
[6] Velikovich, A. L., C. Huete, and J. G. Wouchuk. Effect of shock-generated
turbulence on the Hugoniot jump conditions. Physical Review E 85.1
(2012): 016301.
[7] Huete, César and Jin, Tai and Martínez-Ruiz, Daniel and Luo, Kun.
Interaction of a planar reacting shock wave with an isotropic turbulent
vorticity field. Physical Review E, 96.5 (2017): 053104.](https://image.slidesharecdn.com/wfmacuadra-200928202543/85/Slides-Workshop-on-Fluid-Dynamics-2019-29-320.jpg)