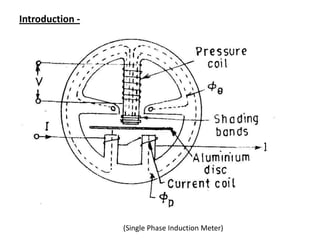
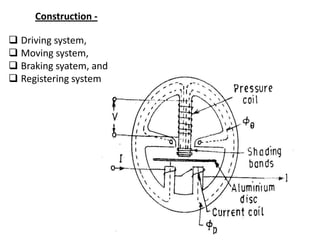
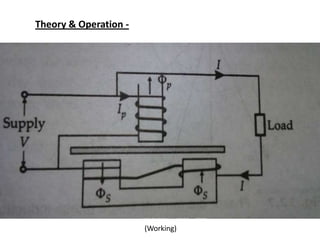
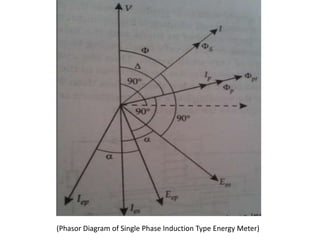
The document summarizes the construction and working of a single phase induction type energy meter. It consists of a driving system, moving system, braking system and registering system. The driving torque is proportional to the supply voltage, load current and their phase difference, causing the disk to rotate. The number of rotations is proportional to the energy consumed. Potential errors include incorrect fluxes/phase angles and friction changes. Adjustments include preliminary light load and creep adjustments to calibrate the meter.

1. EEM
PRESENTATION
ON
INDUCTION TYPE ENERGY METER
PRESENTED BY -

2. Introduction -
(Single Phase Induction Meter)

3. Construction -
 Driving system,
 Moving system,
 Braking syatem, and
 Registering system

4. Theory & Operation -
(Working)

5. (Phasor Diagram of Single Phase Induction Type Energy Meter)

6. Let ,
V = applied voltage
I = load current
ϕ = phase angle of load
IP = pressure coil current
Δ = phase angle between supply voltage and pressure coil flux
f = frequency
Z = impedence of eddy current paths
α = phase angle of eddy current paths
Eep = eddy emf induced by flux Φp
Iep = eddy current due to flux Φp
Ees = eddy emf induced by flux Φs
Ies = eddy current due to flux Φs
Net driving torque,
Td ∝ Φp Φs (f/Z) sinβ cosα
Td = K1 Φp Φs (f/Z) sinβ cosα
Where ,k1 = a constant,
β = phase angle between fluxes Φp and Φs ,
Φs = (Δ- ϕ)

7. • Thus , Driving Torque , Td = K1 Φp Φs (f/Z) sin(Δ- ϕ) cosα
• But Φp ∝ V and Φs ∝ I,
• ∴ Td = K2 V I (f/Z) sin(Δ- ϕ) cosα
• For constants f , Z and α ,
• Td = K3 V I sin(Δ- ϕ)
• If N is the steady speed, braking torque
• Tb = K 4 N
• At steady speed , driving torque = braking torque,
• ∴ K3 V I sin(Δ- ϕ) = K4 N
Thus, N = K V I sin(Δ- ϕ) and
for Δ = 90°
i.e., N = K V I sin(90°- ϕ)

8. • N = K V I cos ϕ
• Now V I cos ϕ = P (Power)
• Or N = K x (Power)
Total number of revolutions = ∫ N dt = K x ∫ (Power) dt = K x (energy)

9. Errors -
 Incorrect magnitude of fluxes,
 Incorrect phase angles,
 Changes in strength of brake magnet,
 Changes in disc resistance,
 Abnormal friction of moving parts
Adjustments -
 Preliminary light load adjustment,
 Light load adjustment,
 Creep adjustment