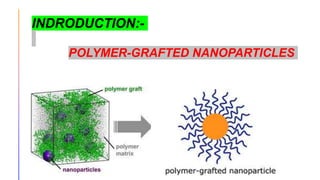
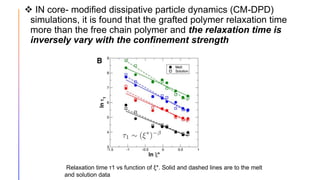
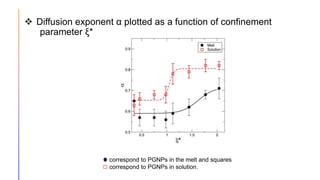
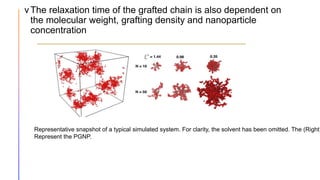
The document discusses the simulation of polymer-grafted nanoparticles (PGNPs) to study the dynamics of polymer chains. The simulation finds that the relaxation time of polymer chains near the nanoparticle surface is longer than those further away due to spatial confinement. It also finds that the relaxation time of grafted polymers is longer than free polymers and decreases with increased confinement. The relaxation processes of PGNPs are found to be Rouse-like in polymer melts and may be Zimm-like in solutions, depending on the confinement parameter. Additional neutron spin echo measurements are suggested to further validate the simulations.

1. CONCEPT IN SOFT MATTER SYSTEM
SIMULATION OF CORONAL DYNAMICS OF POLYMER-
GRAFTED NANOPARTICLE
PRESENTED BY:-
ASHISH KUMAR SINGH
PB22MTECH11003

2. CONTENTS
INDRODUCTION
METHODOLOGY FOR PGNP
APPLICATION
WHY DYNMICS OF POLYMER CHAIN
SIMULATION OUTCOMES
CONCLUSION

3. INDRODUCTION:-
POLYMER-GRAFTED NANOPARTICLES

4. METHODOLOGY FOR PNGP:-

5.  In Development of many advance material
 Antibacterial Material
Biocompatible Material
Sensor Material
APPLICATION:-

6. WHY DYNAMICS OF POLYMER CHAIN:-
Play an important role in-
 Stress relaxation modulus
 Fracture mechanics
 Transport phenomena
 Energy dissipation

7. The Rouse description of the dynamics is based on a friction
coefficient for segments of the polymer chain (ζp) that
scales linearly with the number of monomers in that segment
(i.e., ζp = pζ)
Where
ηs is the local viscosity
b is the Kuhn length
ν is the Flory exponent
N is the degree of polymerization of the chain

8.  The Zimm description of polymer dynamics is based on a
friction coefficient that is proportional to the size of the chain or
segment of interest
 scaling exponent of 3ν instead of 1 + 2ν.
 The Zimm model is most appropriate for solution whereas the
Rouse model is better for polymer melts

9. SIMULATION OUTCOMES:-
v In PGNP, two regions is form in consideration
of the relaxation dynamics of the of the polymer. The region
near the nanoparticle surface is more stretched and
highly dense than the region away from the nanoparticle surface
v Near the nanoparticles surface curvature, the relaxation time is
more than the outer part
v It is found that the relaxation time of the inner regions, relaxation
times were approximately 2-3 times longer than those in the
outer regions

10.  IN core- modified dissipative particle dynamics (CM-DPD)
simulations, it is found that the grafted polymer relaxation time
more than the free chain polymer and the relaxation time is
inversely vary with the confinement strength
Relaxation time τ1 vs function of ξ*. Solid and dashed lines are to the melt
and solution data

11.  Diffusion exponent α plotted as a function of confinement
parameter ξ*
correspond to PGNPs in the melt and squares
correspond to PGNPs in solution.

12. vThe relaxation time of the grafted chain is also dependent on
the molecular weight, grafting density and nanoparticle
concentration
Representative snapshot of a typical simulated system. For clarity, the solvent has been omitted. The (Right)
Represent the PGNP.

13. CONCLUSION:-
 Grafted chains express larger values of Rg than free
chains due to spatial confinement by neighboring chains
 Simulations suggest that for ξ* < 1, the relaxation processes are
Rouse-like regardless of whether the PGNPs are in solution or a
polymer melt
 For ξ* > 1, the relaxation processes are Rouse-like
in the melt and may be Zimm-like in solution
Additional neutron spin echo NSE measurements of PGNPs in both
the melt and solution states would be useful to compare to CM-DPD
simulations
 which predict that the stretching of the grafted chains should be
weaker in the melt and the scaling of τ with q should be stronger than
was measured for PGNPs in solution