The document discusses the Shapeless library in Scala, which provides advanced type-level programming features and compile-time abstractions, using examples to illustrate concepts such as type-safe casting, dependent types, and the implementation of proofs. It explains how to work with natural numbers, hlists, and proofs within Scala's type system, emphasizing the flexibility and power of Shapeless for eliminating boilerplate code and enhancing static reasoning. Furthermore, it covers practical applications, including a typed SQL implementation and type-safe data manipulations.

1. Demystifying
Shapeless
Jared Roesch
@roeschinc
https://github.com/jroesch
1

2. Who I am
2

3. What I do:
PL Lab
3

4. What is Shapeless?
• https://github.com/milessabin/shapeless
• A library from Miles Sabin and co.
• A playground for advanced typed FP
4

5. It has lots of features
5

6. object size extends Poly1 {
implicit def int = at[Int] (x => 1)
implicit def string = at[String] (s => s.length)
implicit def tuple[A, B] = at[(A, B)] (t => 2)
}
!
val list = 1 :: “foo” :: (‘x’, ‘a’) :: HNil
list.map(size) // => 1 :: 3 :: 2 :: HNil
We can do flexible things like:
6

7. Inspiration
• Scrap Your Boilerplate
• Generic Deriving in Haskell
• Dependently typed languages
7

8. Static reasoning
• allows for us to implement powerful compile time
abstractions
• you only pay a minor cost with extra compile time,
and passing around proof terms
8

9. Type safe casting of an arbitrary List to Product:
9
case class Point(x: Int, y: Int)
val xs: List[Any] = List(1,2)
xs.as[Point]
https://gist.github.com/jroesch/52727c6d77a9d98458d5

10. scala> val q = sql("select name, age from person")
scala> q() map (_ get "age")
res0: List[Int] = List(36, 14)
compile time checked SQL:
from: https://github.com/jonifreeman/sqltyped
10

11. Dependent Types
• relaxation of the “phase distinction”
• simply: remove the distinction between types and
values (allow types to depend on values)
• many things billed as type level programming are
attempts at emulating dependent types
11

12. The phase distinction exists in Scala:
!
Vect : (Nat, Type) => Type
!
we would like to write something like this:
!
trait Vect[N <: Nat, A]
!
we are still writing this:
!
Vect : (Type, Type) => Type
12

13. Types as Logic
• type systems == logical framework
• types correspond to propositions, and programs to
proofs
• types can be boring (i.e Int, String, User); not all
proofs are interesting
13

14. How do we emulate
dependent types?
• We still have the phase distinction to get around
• We need to promote values to the type level (i.e 0
can either act as a value or type)
• Vect[0, Int] and val x = 0
14

15. Nat
• Natural numbers (0, 1 …)
• Let’s look at both the value level and the type level
• We need these to reason about numeric constraints
like size, ordering, indexing, and so on.
• Usually represented by a Zero element and a
Successor function.
15

16. sealed trait Nat
case object Zero extends Nat
case class Succ(n : Nat) extends Nat
16
A value representing a Natural number:

17. How do we encode a type level representation of naturals?
17

18. Prerequisites
‣ implicit arguments
‣ sub-typing, and bounded polymorphism
‣ type members
‣ structural refinement types
‣ path dependent types
18

19. implicit val x: Int = 10
!
def needsImplicit(implicit ev: Int) = ???
implicit arguments allow us to pass extra parameters
around with help of the compiler:
19

20. type members allow for values to have type information:
trait User { type Email; val email : Email }
!
20

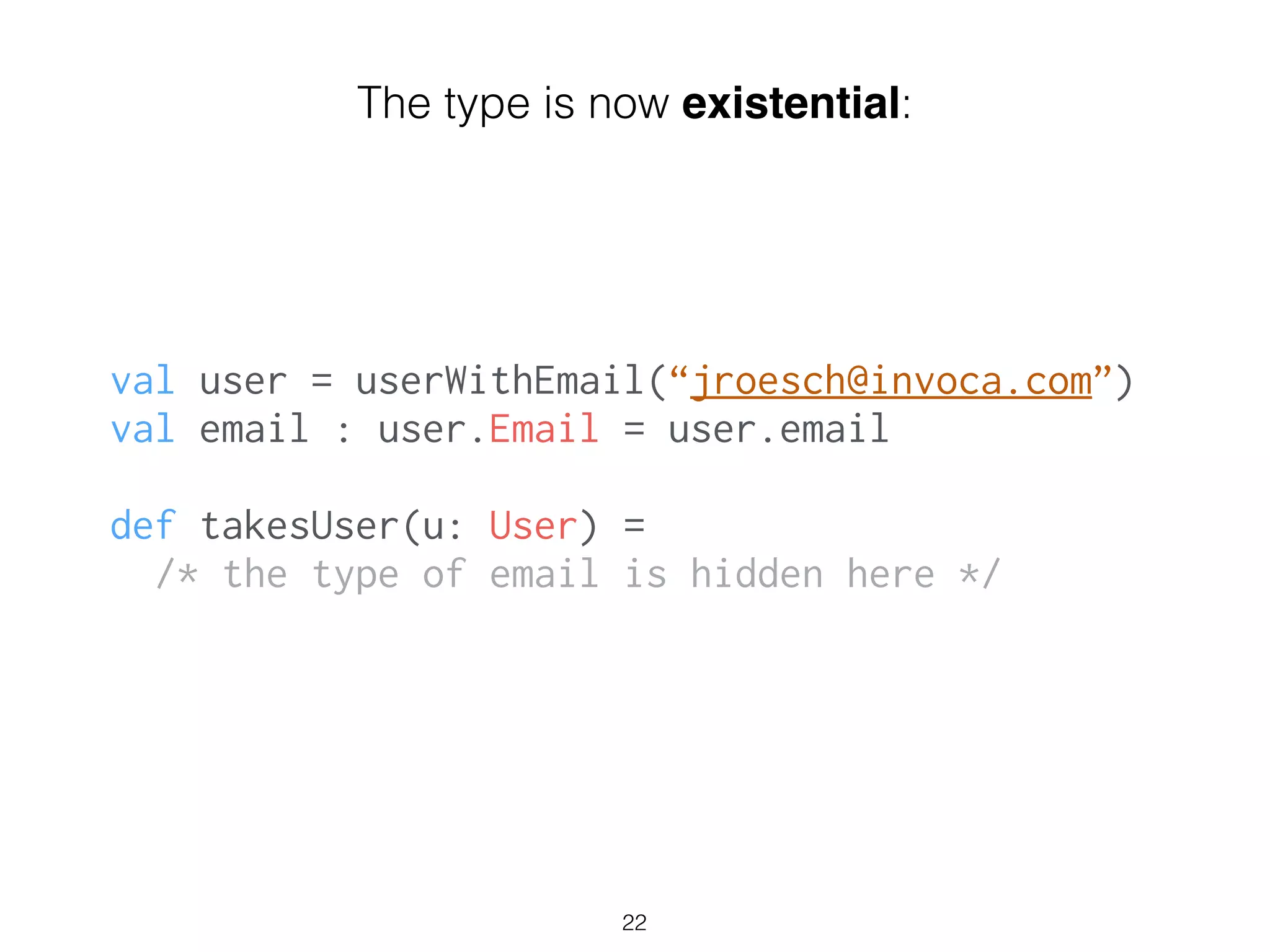
21. def userWithEmail[E](e : E) = new User {
type Email = E
val email = e
}
!
21
We make a type part of the value:

22. val user = userWithEmail(“jroesch@invoca.com”)
val email : user.Email = user.email
!
def takesUser(u: User) =
/* the type of email is hidden here */
22
The type is now existential:

23. also we make use of structural refinement types:
sealed trait Database
!
sealed trait Postgres extends Database
case object Postgres extends Postgres
!
sealed trait MySQL extends Database
case object MySQL extends MySQL
!
trait DataStore { type DB <: Database … }
23

24. // Refined type
type PostgreSQL = DataStore { type DB = Postgres }
!
def writeJSONB(ds: PostgreSQL, jsonb: JSONB) = ???
def dontCare(ds: DataStore, …) = ???
!
val postgres: PostgresSQL = new DataStore { … }
!
val otherDataStore = new DataStore { … }
!
writeJSONB(postgres, value) //works
writeJSONB(otherDataStore, value) //fails
24
We can use this to make our type more specific:

25. trait Unrefined
type Refined = Unrefined { type T = String }
!
implicitly[Refined <:< Unrefined]
25
refined types are subtypes of unrefined types:

26. trait ObligationFor[N <: Nat]
!
def proof[N <: Nat](implicit ev: ObligationFor[N])
26
we can use this sub-typing rule and type bounds to our
advantage during implicit selection:
vs
def proof(implicit ev: ObligationFor[Nat])

27. /* Shapeless Typelevel Natural */
trait Nat {
type N <: Nat
}
!
class _0 extends Nat {
type N = _0
}
!
class Succ[P <: Nat]() extends Nat {
type N = Succ[P]
}
27

28. implicit def intToNat(i: Int): Nat = …
!
val n: Nat = 1
!
type One = n.N // Succ[_0]
28
We can add an implicit conversion for Naturals:

29. def lessThan(n: Nat, m: Nat): Bool =
match (n, m) {
case (Zero, Succ(_)) =>
true
case (Succ(np), Succ(mp)) =>
lessThan(np, mp)
case (_, _) =>
false
}
How do we translate a value level algorithm to one
that constructs a proof object instead
29

30. How do we translate this piece of code?
30

31. trait LessThan[N <: Nat, M <: Nat]
31
Take our proof and translate it to a type:

32. // Typelevel LessThan
trait LessThan[N <: Nat, M <: Nat]
!
// We need ways to construct our proofs.
implicit def lessThanBase[M <: Nat] =
new LessThan[_0, Succ[M]] {}
!
implicit def lessThanStep[N <: Nat, M <: Nat]
(implicit lessThanN: LessThan[N, M]) =
new LessThan[Succ[N], Succ[M]] {}
!
def lessThan(n : Nat, m : Nat)
(implicit lessThan: LessThan[n.N, m. N]): Boolean =
true
32

33. HList
sealed trait HList
!
case class ::[+H, +T <: HList](head : H, tail : T)
extends HList
!
sealed trait HNil extends HList
case object HNil extends HNil
33

34. import shapeless._
!
val xs : Int :: String :: HNil = 1 :: “foo” :: HNil
34

35. trait IsHCons[L <: HList] {
type H
type T <: HList
def head(l : L) : H
def tail(l : L) : T
}
35

36. object IsHCons {
…
!
type Aux[L <: HList, Head, Tail <: HList] =
IsHCons[L] { type H = Head; type T = Tail }
!
implicit def hlistIsHCons[Head, Tail <: HList] =
new IsHCons[Head :: Tail] {
type H = Head
type T = Tail
def head(l : Head :: Tail) : H = l.head
def tail(l : Head :: Tail) : T = l.tail
}
}
36

37. def head(implicit c : IsHCons[L]) : c.H = c.head(l)
!
def tail(implicit c : IsHCons[L]) : c.T = c.tail(l)
We then demand proof when we implement methods on
HList’s:
37

38. Proofs as black boxes
• Proof objects can be treated as black boxes, we
only need to know what relationship they express,
not proof details.
• We can use shapeless as a standard library of
useful tools.
38

39. case class Point(x: Int, y: Int)
!
val generic = Generic.Aux[Point, Int :: Int :: HNil] =
Generic[Point]
!
val point = Point(1,2)
!
val list: Int :: Int :: HNil = generic.to(point)
!
assert(generic.from(list) == point)
39

40. Applying it
• We can build things using many of the same ideas
• typed SQL, JSON with schema, static string
encoding, and plenty of other uses (ex. Spray)
40

41. 41
sealed trait Encoding
…
!
trait EncodedString[E <: Encoding] { … }
…
!
def staticEncoding[E <: Encoding](enc: E, s: String)
= macro StaticEncoding.encodeAs[E]

42. 42
trait Transcode[Initial <: Encoding] {
type Result <: Encoding
!
def transcode(s: EncodedString[Initial]):
EncodedString[Result]
}

43. 43
trait Concatable[Prefix <: Encoding, Suffix <: Encoding] {
type Result <: Encoding
/* Concat is a little verbose, we just ask for
both our strings. */
def concat(s1: EncodedString[Prefix],
s2: EncodedString[Suffix])
/* We get proof that a transcode can happen for both */
(implicit t1: Transcode.Aux[Prefix, Result]
t2: Transcode.Aux[Suffix, Result]):
/* And we get the result */
EncodedString[Result]
}

44. 44
def concat[E1 <: Encoding, E2 <: Encoding]
(s1: EncodedString[E1], s2: EncodedString[E2])
(implicit c: Concatable[E1, E2]) =
c.concat(s1, s2)

45. An extended example
• Let’s encode a proof that one HList is a subset of
another HList.
• But is it useful?
45

46. Imagine our own implementation of a SQL DSL:
!
case class User(
id: Id
name: String,
age: Int,
email: String,
deviceId: Long
)
!
// Create Table
SQL.create[User]
!
SQL.insert(
User(1, “Jared”, 21, “jroesch@cs.ucsb.edu”, 1)
)
!
// successful update
SQL.update[User](“id” ->> 1, “age” ->> 22)
!
// fails to compile
SQL.update[User](“id” ->> 1, bogusField” ->> 1337)
!
… // Queries and so on
46

47. // successful update
SQL.update[User](“id” ->> 1, “age” ->> 22)
!
// fails to compile
SQL.update[User](“id” ->> 1, bogusField” ->> 1337)
47

48. 48
def subList[A](sub: List[A], list: List[A]): Boolean =
(sub, list) match {
case (Nil, _) =>
true
case (x :: xs, y :: ys) if x == y =>
true && subList(xs, ys)
case (subp, first :: remanning) =>
subList(subp, remaining)
}

49. 49
trait SubSeq[Sub <: HList, Super <: HList]

50. 50
object SubSeq extends LowPrioritySubSeq {
type Aux[L <: HList, S <: HList] = SubSeq[L] {
type Sub = S
}
…
}

51. 51
/* Low priority case where we just keep scanning the list. */
trait LowPrioritySubSeq {
implicit def hconsSubSeq[Sub <: HList, SH, ST <: HList]
(implicit subseq: SubSeq.Aux[Sub, ST]) =
new SubSeq[Sub] {
type Sub = SH :: ST
}
}

52. 52
object SubSeq extends LowPrioritySubSeq {
…
/* HNil is a SubSeq of any HList */
implicit def hnilSubSeq[H <: HList] =
new SubSeq[HNil] {
type Sub = H
}
!
…
}

53. 53
object SubSeq extends LowPrioritySubSeq {
…
implicit def hconsSubSeqIso
[H, SH, T <: HList, ST <: HList]
(implicit iso: H =:= SH,
subseq: SubSeq.Aux[T, ST]) =
new SubSeq[H :: T] {
type Sub = SH :: ST
}
}

54. 54
There are few ways to improve upon our last example, I’ll
leave it as a fun puzzle for you.

55. 55
https://gist.github.com/jroesch/db2674d0ef3e49d43154
!
https://github.com/jroesch/scala-by-the-bay-2014

56. Acknowledgements
• Thanks to Miles Sabin, the PL Lab, Adelbert
Chang, and Pete Cruz.
56

57. Thank you for your time, questions?
57