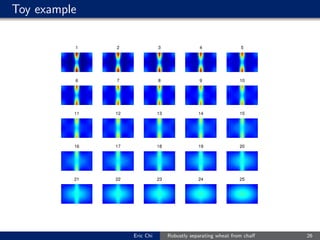
The document discusses methods for separating systematic variation ("wheat") from non-systematic variation ("chaff") in multiway data. It compares using least squares versus least 1-norm optimization to fit multilinear models to data. Least squares assumes Gaussian errors and can be biased by outliers, while least 1-norm is more robust but computationally more difficult. It demonstrates on a toy example how least 1-norm better extracts the underlying signal when the errors are non-Gaussian. The document advocates considering robust loss functions beyond least squares for real-world data that may violate Gaussian assumptions.

1. Robustly separating the wheat from the chaff in
multiway data
Eric C. Chi with Tamara G. Kolda
October 11, 2010
Eric Chi Robustly separating wheat from chaff 1

2. Wheat, Chaff, and fitting models to data
World View
“Wheat” “Chaff”
Data = Systematic Variation + non-Systematic Variation
Eric Chi Robustly separating wheat from chaff 2

3. Wheat, Chaff, and fitting models to data
World View
“Wheat” “Chaff”
Data = Systematic Variation + non-Systematic Variation
This talk
Systematic Variation (Wheat): multilinear
Eric Chi Robustly separating wheat from chaff 2

4. The “best” multilinear fit to the data
Which multilinear model “best” fits the data?
Measure of lack of fit: loss
Many choices:
2-norm
1-norm
Different losses = different assumptions about the statistical behavior
of the non-Systematic variation (Chaff).
Eric Chi Robustly separating wheat from chaff 3

5. The “best” multilinear fit to the data
Which multilinear model “best” fits the data?
Measure of lack of fit: loss
Many choices:
2-norm
1-norm
Different losses = different assumptions about the statistical behavior
of the non-Systematic variation (Chaff).
Why is this important?
Poor separation of wheat and chaff if chaff does not behave as
expected.
Eric Chi Robustly separating wheat from chaff 3

6. Many ways to extract wheat from the data
min
u i
(xi − u)2
Eric Chi Robustly separating wheat from chaff 4

7. Extract wheat with least squares
min
u i
(xi − u)2
Least Squares Solution 1
Eric Chi Robustly separating wheat from chaff 5

8. What happens if we spike the data with outliers?
min
u i
(xi − u)2
Least Squares Solution 1
Eric Chi Robustly separating wheat from chaff 6

9. Least squares is sensitive to outliers.
min
u i
(xi − u)2
Least Squares Solution 1
Least Squares Solution 2
Eric Chi Robustly separating wheat from chaff 7

10. Extract wheat with least 1-norm
min
u i
|xi − u|
Least Squares Solution 1
Least 1−norm Solution
Eric Chi Robustly separating wheat from chaff 8

11. When is a least squares solution the “best” solution?
Least Squares (LS) Solution = most “likely” u when
non-Systematic Variation is Gaussian.
The least squares solution is the maximum likelihood estimate (mle)
of u:
xi = u + ei .
where ei ∼ i.i.d. N(0,1).
Eric Chi Robustly separating wheat from chaff 9

12. When is a least 1-norm solution the “best” solution?
Least 1-norm Solution = mle of u when
non-Systematic Variation is Laplacian.
xi = u + ei .
where ei
i.i.d.
∼ f (x) = exp(−|x|)/2.
Eric Chi Robustly separating wheat from chaff 10

13. Gaussian and Laplacian densities
e
density
0.0
0.1
0.2
0.3
0.4
0.5
−6 −4 −2 0 2 4 6
Eric Chi Robustly separating wheat from chaff 11

14. Justifying the Gaussian assumption
STAT 101
non-Systematic variation = accumulation of many small random effects
Eric Chi Robustly separating wheat from chaff 12

15. Justifying the Gaussian assumption
STAT 101
non-Systematic variation = accumulation of many small random effects
(Central Limit Theorem)
Eric Chi Robustly separating wheat from chaff 12

16. Justifying the Gaussian assumption
STAT 101
non-Systematic variation = accumulation of many small random effects
(Central Limit Theorem)
Practice
Least squares is easy and fast to compute
Eric Chi Robustly separating wheat from chaff 12

17. Justifying the Gaussian assumption
STAT 101
non-Systematic variation = accumulation of many small random effects
(Central Limit Theorem)
Practice
Least squares is easy and fast to compute (Convenience).
Eric Chi Robustly separating wheat from chaff 12

18. Assumptions: multilinear wheat
Example: Iris data
150 samples of 3 species of iris flowers
4 measurements on sepal and petal dimensions
Data is a two-way array: X ∈ R150×4
Bilinear wheat (rank 2)
X ≈ u1 ◦ v1 + u2 ◦ v2
xij ≈ ui1vj1 + ui2vj2
u1, u2 ∈ R150
v1, v2 ∈ R4
Eric Chi Robustly separating wheat from chaff 13

19. Extracting bilinear wheat with least squares
min
150
i=1
4
j=1
(xij −
2
r=1
uir vjr )2
ui1
ui2
−1.0
−0.5
0.0
0.5
1.0
q
qq
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
qq
q q
q
q
q
q
q
qq
q
q
q
q
q
q
q
q
qq
q
q
q
q
q
q
q
q
q
−3 −2 −1 0 1 2 3
Eric Chi Robustly separating wheat from chaff 14

20. CANDECOMP/PARAFAC (CP) Decomposition
Example: Video surveillance
256 × 256 pixel images at 200 time points.
Data is a three-way array: X ∈ R256×256×200.
Trilinear wheat (rank 5)
X ≈ u1 ◦ v1 ◦ w1 + · · · + u5 ◦ v5 ◦ w5.
xijk ≈ ui1vj1wk1 + ui2vj2wk2 + · · · + ui5vj5wk5
u1, u2, . . . , u5 ∈ R256
v1, v2, . . . , v5 ∈ R256
w1, w2, . . . , w5 ∈ R200
Eric Chi Robustly separating wheat from chaff 15

21. Extracting multilinear wheat
Least Squares
min
256
i=1
256
j=1
200
k=1
(xijk −
5
r=1
uir vjr wkr )2
Eric Chi Robustly separating wheat from chaff 16

22. Extracting multilinear wheat
Least Squares
min
256
i=1
256
j=1
200
k=1
(xijk −
5
r=1
uir vjr wkr )2
Least 1-norm
min
256
i=1
256
j=1
200
k=1
|xijk −
5
r=1
uir vjr wkr |
Eric Chi Robustly separating wheat from chaff 16

23. Violating Gaussian assumptions: Who cares?
What if the non-Systematic variation is really non-Gaussian?
Neuroimaging: Movement artifacts.
Video Surveillance: Foreground/Background separation.
non-Gaussian how?
Sparse large perturbations.
Perturbations are large but not too large.
Eric Chi Robustly separating wheat from chaff 17

24. Minimizing the 1-norm loss
Least 1-norm is harder to solve than Least Squares!
The loss is non-differentiable.
Smooth approximation to 1-norm
ijk
xijk −
R
r=1
uir vjr wkr ≈
ijk
xijk −
R
r=1
uir vjr wkr
2
+
for small > 0.
Eric Chi Robustly separating wheat from chaff 18

25. Majorization-Minimization
Solve a hard optimization problem
ijk
xijk −
R
r=1
uir vjr wkr
2
+
as a series of easy ones (weighted least squares).
Minimize surrogate loss functions (quadratic functions).
Eric Chi Robustly separating wheat from chaff 19

26. MM Algorithm
Loss =
i
(xi − u)2 +
u
Loss
Less
More
very bad optimal less bad
Eric Chi Robustly separating wheat from chaff 20

27. MM Algorithm
Loss =
i
(xi − u)2 +
u
Loss
Less
More
very bad optimal less bad
q
Eric Chi Robustly separating wheat from chaff 21

28. MM Algorithm
Loss =
i
(xi − u)2 +
u
Loss
Less
More
very bad optimal less bad
q
Eric Chi Robustly separating wheat from chaff 22

29. MM Algorithm
Loss =
i
(xi − u)2 +
u
Loss
Less
More
very bad optimal less bad
q
Eric Chi Robustly separating wheat from chaff 23

30. MM Algorithm
Loss =
i
(xi − u)2 +
u
Loss
Less
More
very bad optimal less bad
q
Eric Chi Robustly separating wheat from chaff 24

31. Toy example
X ∈ R25×25×25
Slice = mix of A and B.
Eric Chi Robustly separating wheat from chaff 25

32. Toy example
1
6
11
16
21
2
7
12
17
22
3
8
13
18
23
4
9
14
19
24
5
10
15
20
25
Eric Chi Robustly separating wheat from chaff 26

33. Toy example: Trilinear Wheat + Gaussian Chaff
1
6
11
16
21
2
7
12
17
22
3
8
13
18
23
4
9
14
19
24
5
10
15
20
25
Eric Chi Robustly separating wheat from chaff 27

34. Toy example: A slice up close
Observed True Wheat Gauassian Chaff
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
Eric Chi Robustly separating wheat from chaff 28

35. Extracting from Gaussian Chaff by Least Squares
Observed Extracted Wheat Difference
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
Eric Chi Robustly separating wheat from chaff 29

36. Extracting from Gaussian Chaff by Least 1-norm
Observed Extracted Wheat Difference
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
Eric Chi Robustly separating wheat from chaff 30

37. Trilinear wheat + non-Gaussian Chaff
1
6
11
16
21
2
7
12
17
22
3
8
13
18
23
4
9
14
19
24
5
10
15
20
25
Eric Chi Robustly separating wheat from chaff 31

38. Extracting from non-Gaussian Chaff by Least Squares
Observed Extracted Wheat Difference
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
Eric Chi Robustly separating wheat from chaff 32

39. Extracting from non-Gaussian Chaff by Least 1-norm
Observed Extracted Wheat Difference
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
Eric Chi Robustly separating wheat from chaff 33

40. Caveats
Costs
Computational: 1-norm minimization is more work than least squares.
Statistical: Robustness versus efficiency tradeoff
Limitations
Trouble with sparse tensor data.
Best suited for dense tensor data?
Eric Chi Robustly separating wheat from chaff 34

41. Summary
Least Squares (i.i.d. Gaussian errors)
Wide applicability, easy to compute solution, statistical efficiency.
But not always appropriate.
Observed Extracted Wheat Difference
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
Eric Chi Robustly separating wheat from chaff 35

42. Summary
Least 1-norm (i.i.d. Laplacian errors)
Can accomodate Gaussian errors and non-Gaussian errors.
But not as easy to compute, less statistical efficiency.
Observed Extracted Wheat Difference
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
5 10 15 20 25
5
10
15
20
25
Eric Chi Robustly separating wheat from chaff 36

43. Future Work
Real data
More sophisticated robust loss functions: β divergences
Robust factorizations for data on different scales:
Binary
Non-negative data.
Eric Chi Robustly separating wheat from chaff 37

44. Thank you!
Observed Extracted Wheat Difference
Images from wikipedia.org
Eric C. Chi
echi@rice.edu
Eric Chi Robustly separating wheat from chaff 38