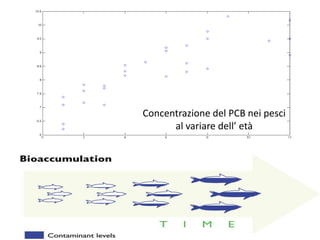
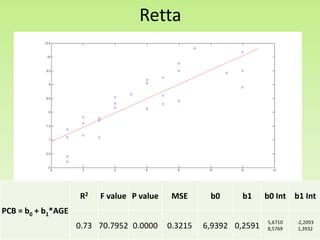
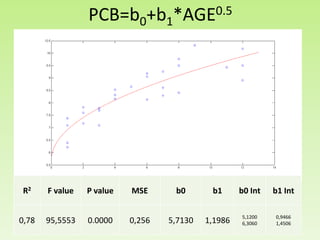
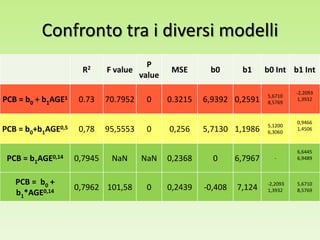
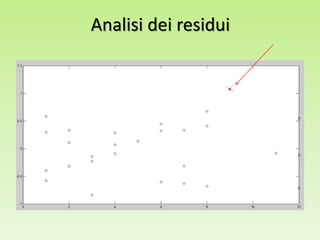
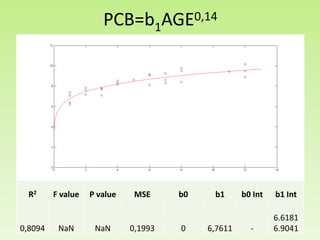
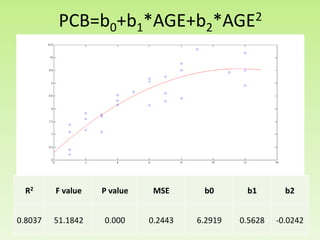
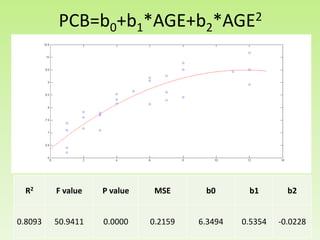
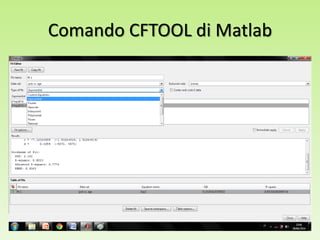
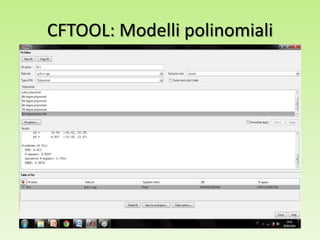
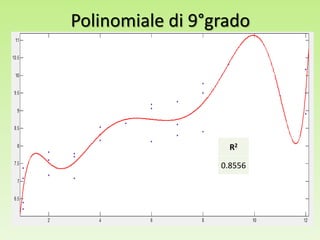
Il progetto analizza la correlazione tra la concentrazione di PCB nelle trote del lago Cayuga e l'età del pesce, utilizzando regressioni lineari e modelli polinomiali per la stima dei parametri. I risultati mostrano che il modello con esponente 0.14 fornisce il miglior valore di R2, pari a 0.8095, e una buona capacità predittiva. L'analisi dei residui e le comparison tra diversi modelli evidenziano l'importanza di considerare la variazione non lineare nei dati.

1. PROGETTO 2
Federico Diana
Fabio Fanari
Gerardo de Leon
Analisi dei Processi Chimici e Biotecnologici
Prof. Massimiliano Grosso
Gruppo
Ronald Fisher

2. Scopo del Progetto
Partendo da dei dati sulla concentrazione di
residui di PCB misurati nelle trote del lago
Cayuga (NY), individuare la correlazione che
meglio descriva la variazione della
concentrazione del pcb nelle carni del pesce al
variare dell’ età, effettuando delle regressioni
lineari per la stima dei parametri del modello.

3. Concentrazione del PCB nei pesci
al variare dell’ età

4. Parametri utilizzati per la stima della
bontà del modello
• R2
• F
• P-value
• MSE
• Residui
• Intervalli di fiducia dei coefficienti
Strumento utilizzato:
Toolbox statistics di Matlab

5. Retta
PCB = b0 + b1*AGE
R2 F value P value MSE b0 b1 b0 Int b1 Int
0.73 70.7952 0.0000 0.3215 6,9392 0,2591 5,6710
8,5769
-2,2093
1,3932

6. PCB=b0+b1*AGE0.5
R2 F value P value MSE b0 b1 b0 Int b1 Int
0,78 95,5553 0.0000 0,256 5,7130 1,1986 5,1200
6,3060
0,9466
1,4506

7. Ricerca dell’esponente
PCB=a*Ageb
Maneggiando le variabili:
log(PCB)=log(a*Ageb)=log(a)+b*log(Age)
con log(PCB)=y ; log(a)=b0 ; b=b1 ; log(Age)=x ;
=> y=b0+b1*x
E facendone la regressione lineare possiamo ricercare il nostro
esponente:
=> b1 = 0.14

8. Confronto tra i diversi modelli
R2 F value
P
value
MSE b0 b1 b0 Int b1 Int
PCB = b0 + b1AGE1 0.73 70.7952 0 0.3215 6,9392 0,2591 5,6710
8,5769
-2,2093
1,3932
PCB = b0+b1AGE0,5 0,78 95,5553 0 0,256 5,7130 1,1986 5,1200
6,3060
0,9466
1,4506
PCB = b1AGE0,14 0,7945 NaN NaN 0,2368 0 6,7967 -
6,6445
6,9489
PCB = b0 +
b1*AGE0,14
0,7962 101,58 0 0,2439 -0,408 7,124 -2,2093
1,3932
5,6710
8,5769

9. Analisi dei residui

10. PCB=b1AGE0,14
R2 F value P value MSE b0 b1 b0 Int b1 Int
0,8094 NaN NaN 0,1993 0 6,7611 -
6.6181
6.9041

11. Eliminazione del punto isolato
R2 F value P value MSE b0 b1 b0 Int b1 Int
PCB = b0 +
b1*AGE0,14
0,8095 106,2058 0.000 0,2072 -0,0883 6,8322
-1.77
1.59
5.4668
8.1976
PCB = b1AGE0,14
0,8094 NaN NaN 0,1993 0 6,7611 -
6.6181
6.9041

12. PCB=b0+b1*AGE+b2*AGE2
R2 F value P value MSE b0 b1 b2
0.8037 51.1842 0.000 0.2443 6.2919 0.5628 -0.0242

13. PCB=b0+b1*AGE+b2*AGE2
R2 F value P value MSE b0 b1 b2
0.8093 50.9411 0.0000 0.2159 6.3494 0.5354 -0.0228

14. Comando CFTOOL di Matlab

15. CFTOOL: Modelli polinomiali

16. Polinomiale di 9°grado
R2
0.8556

17. Grazie per l’attenzione!
Muchas Gracias!