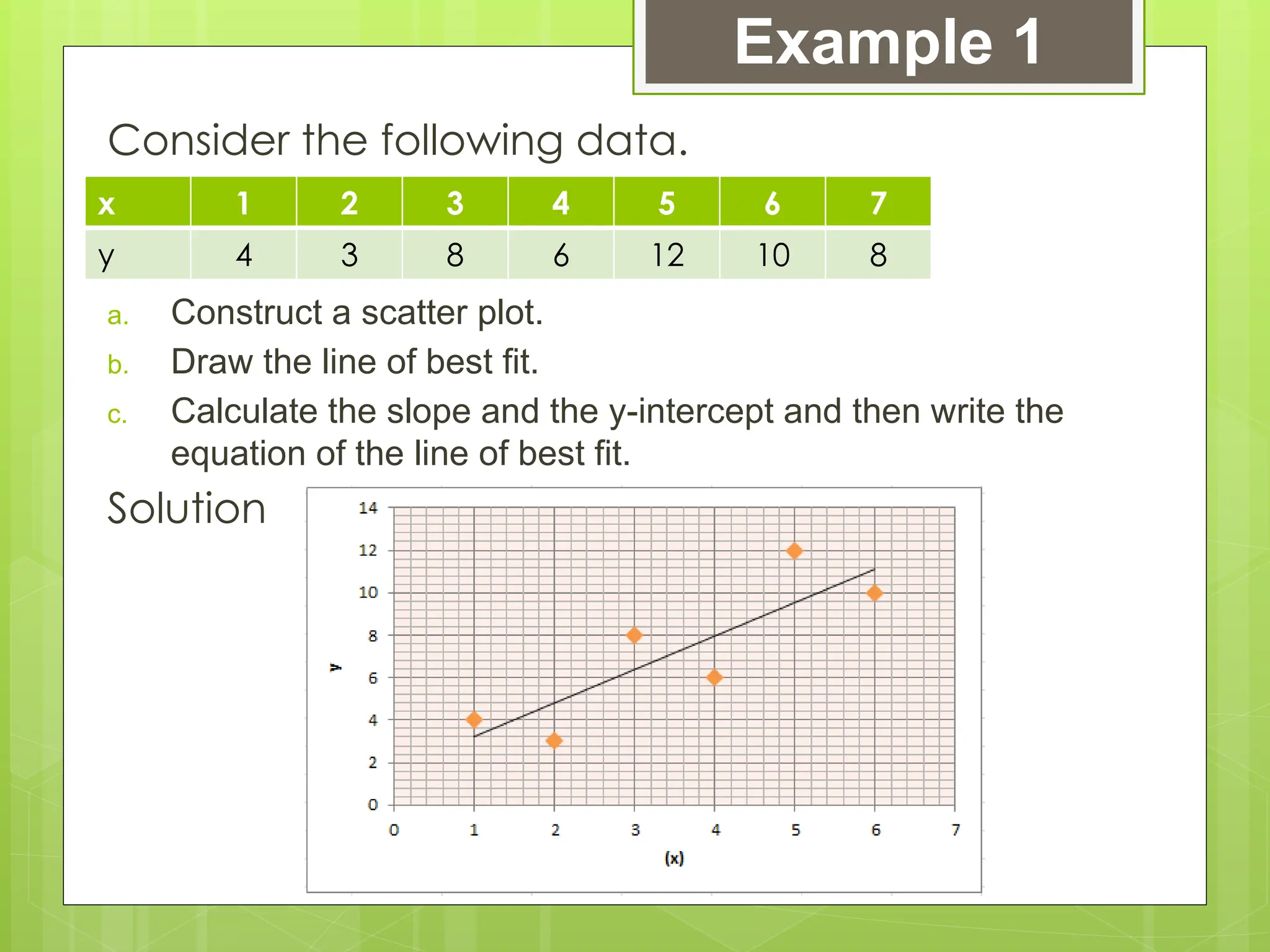
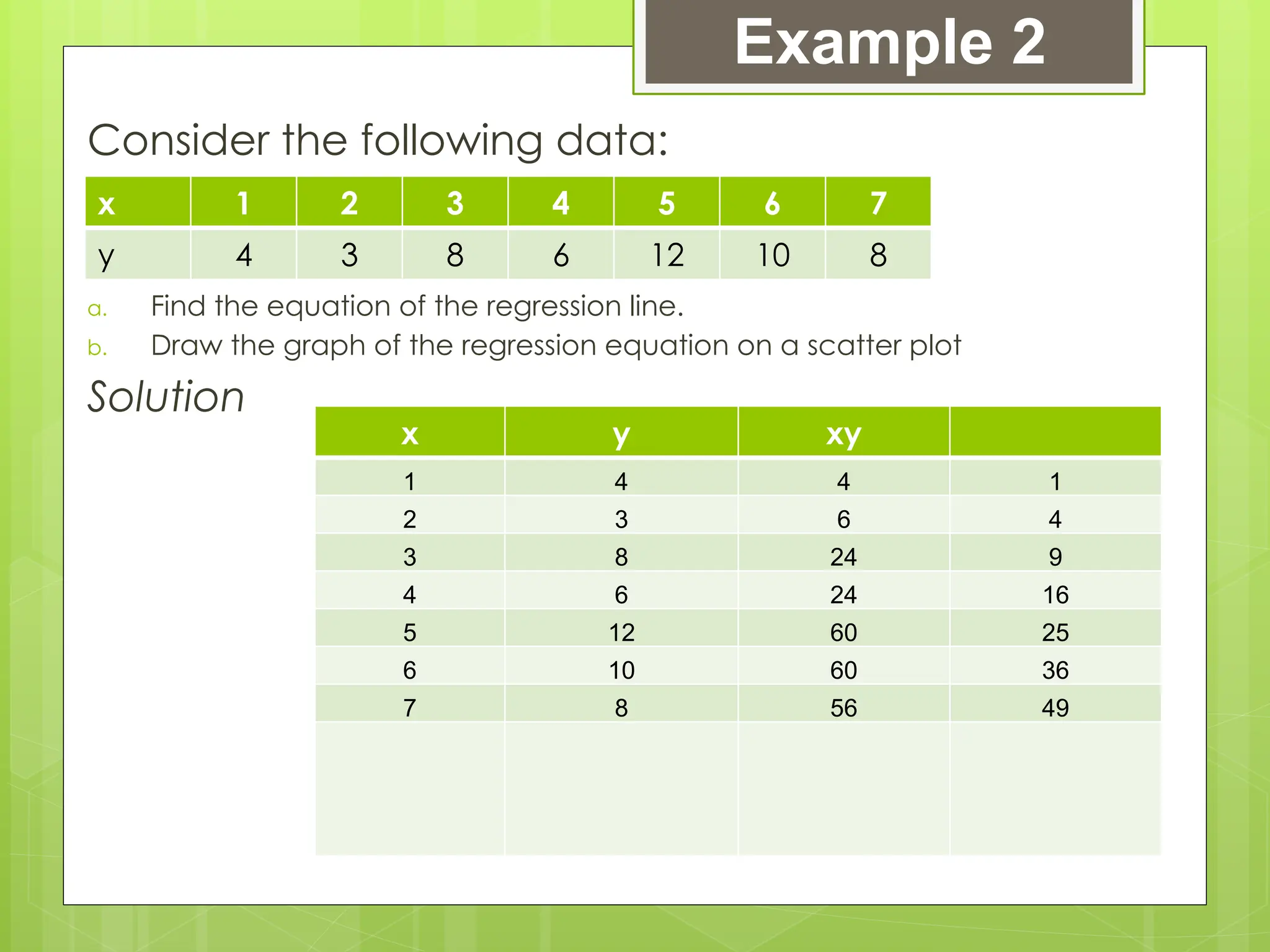
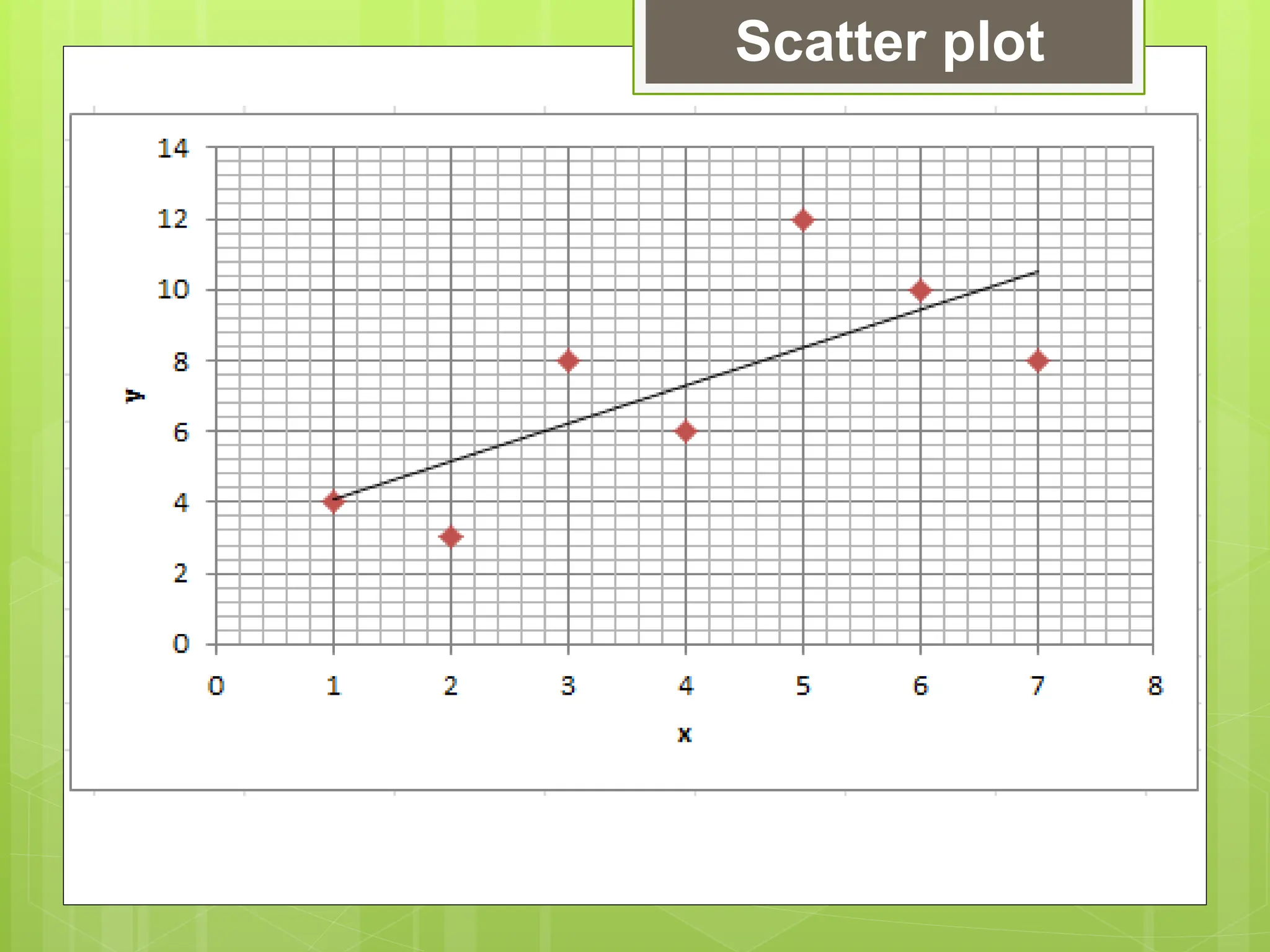
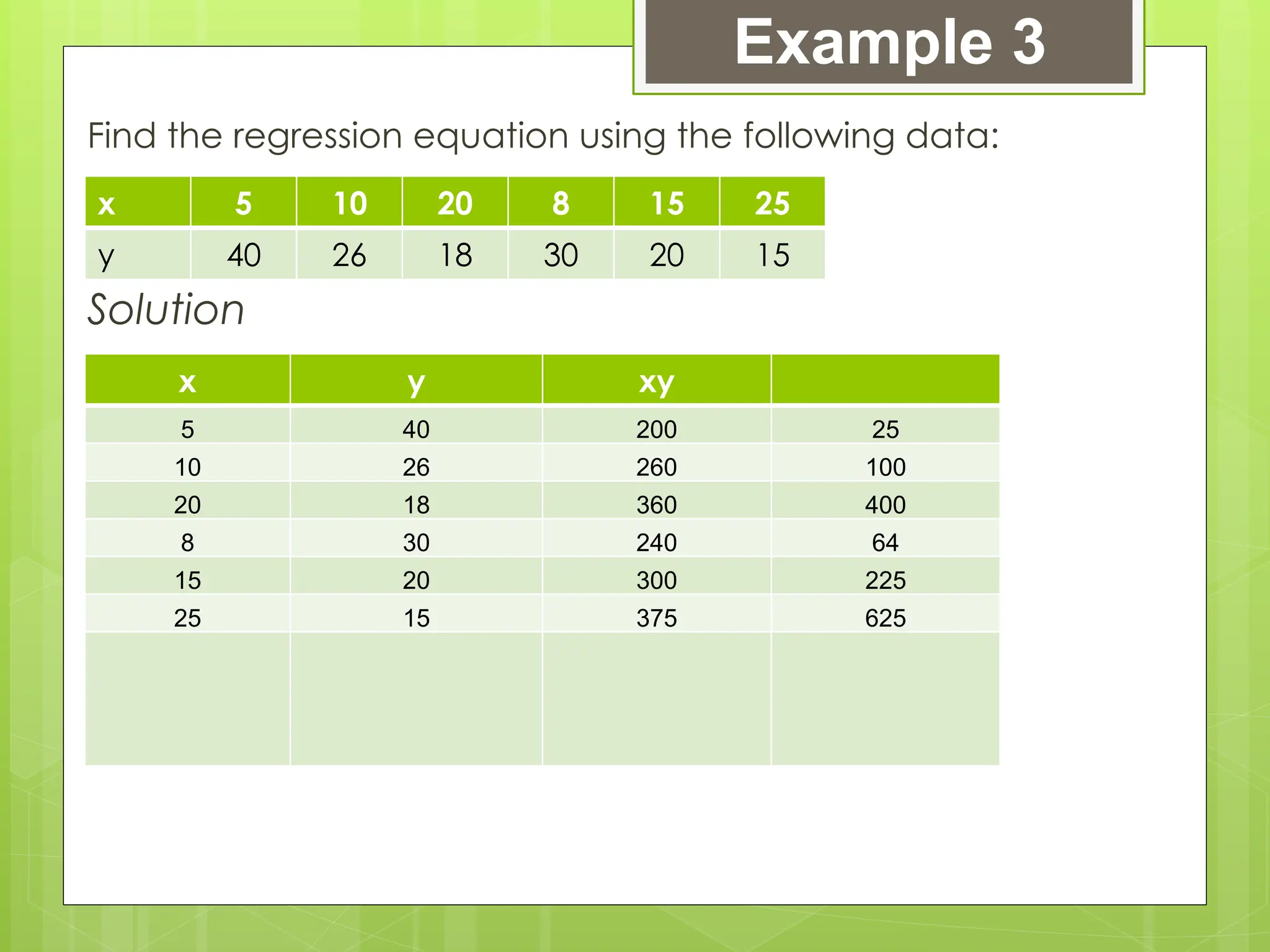
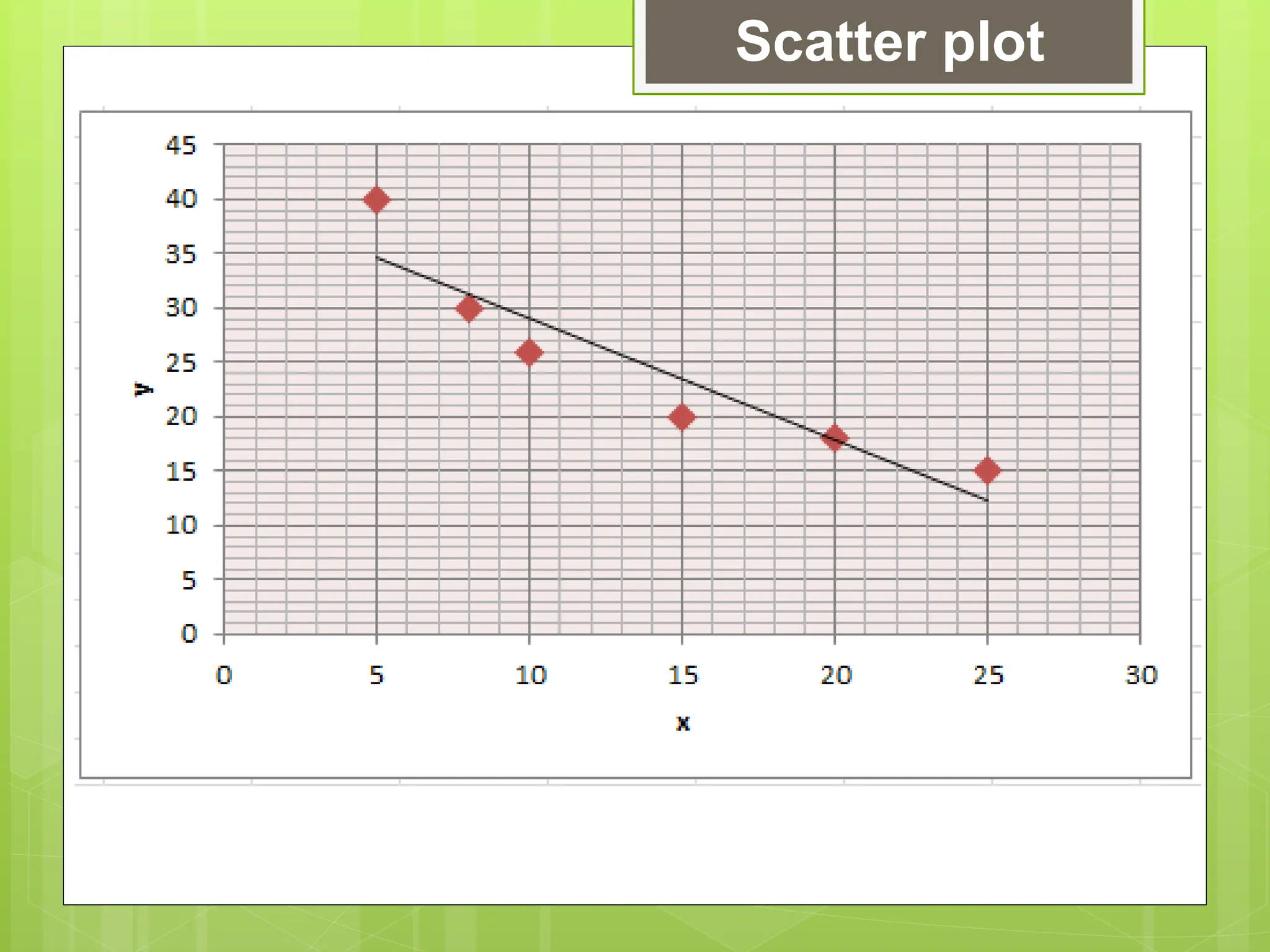
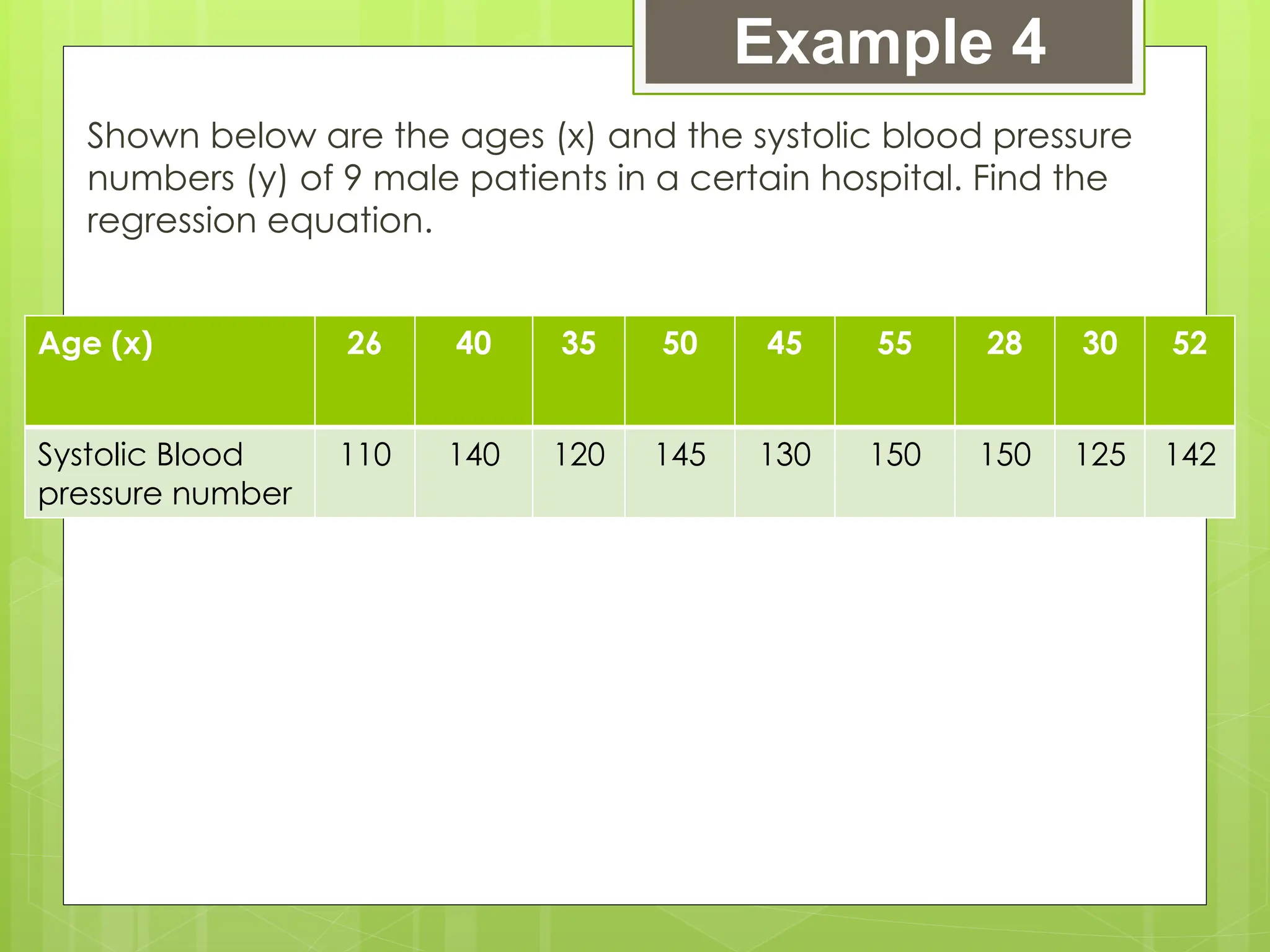
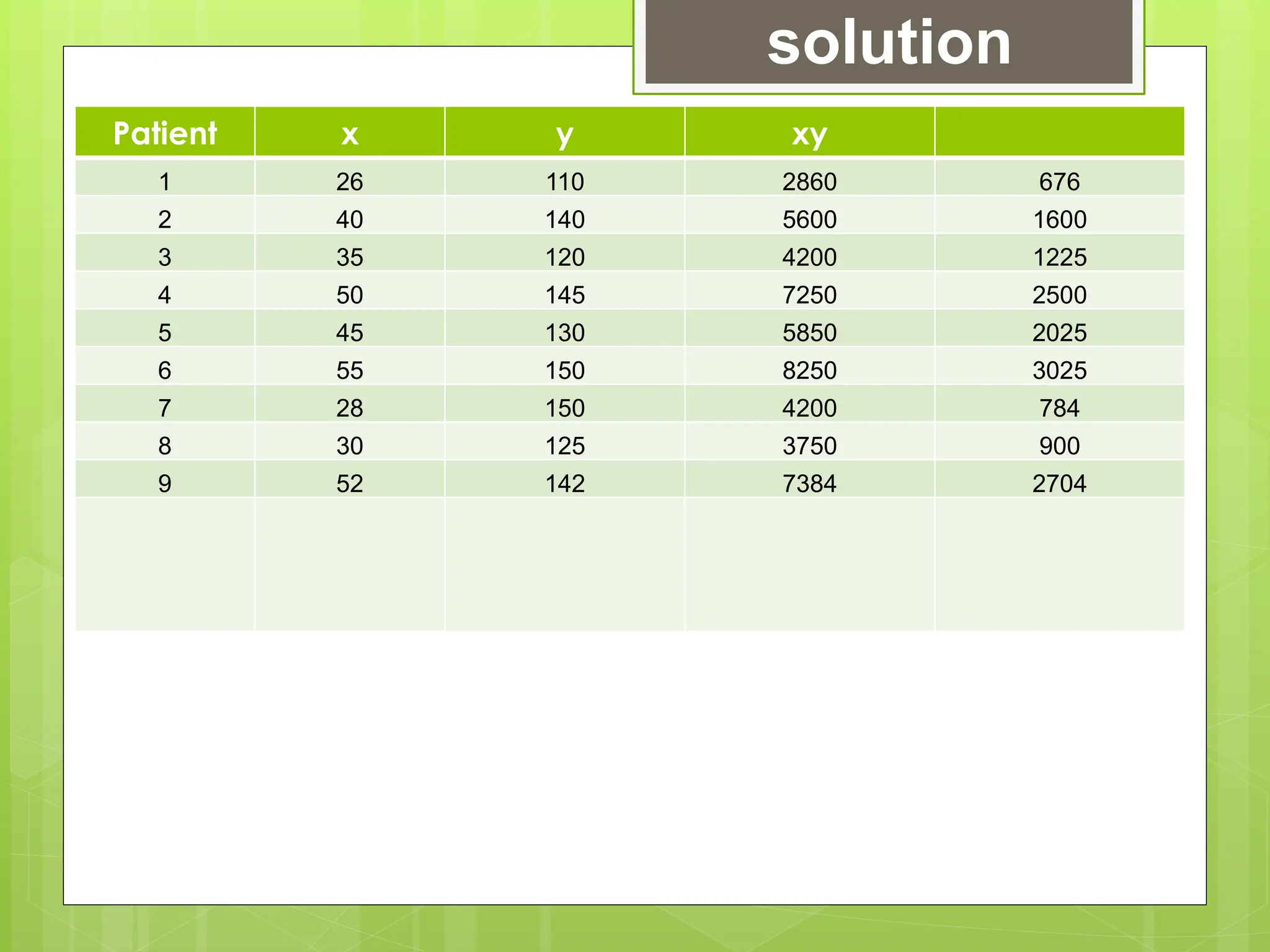
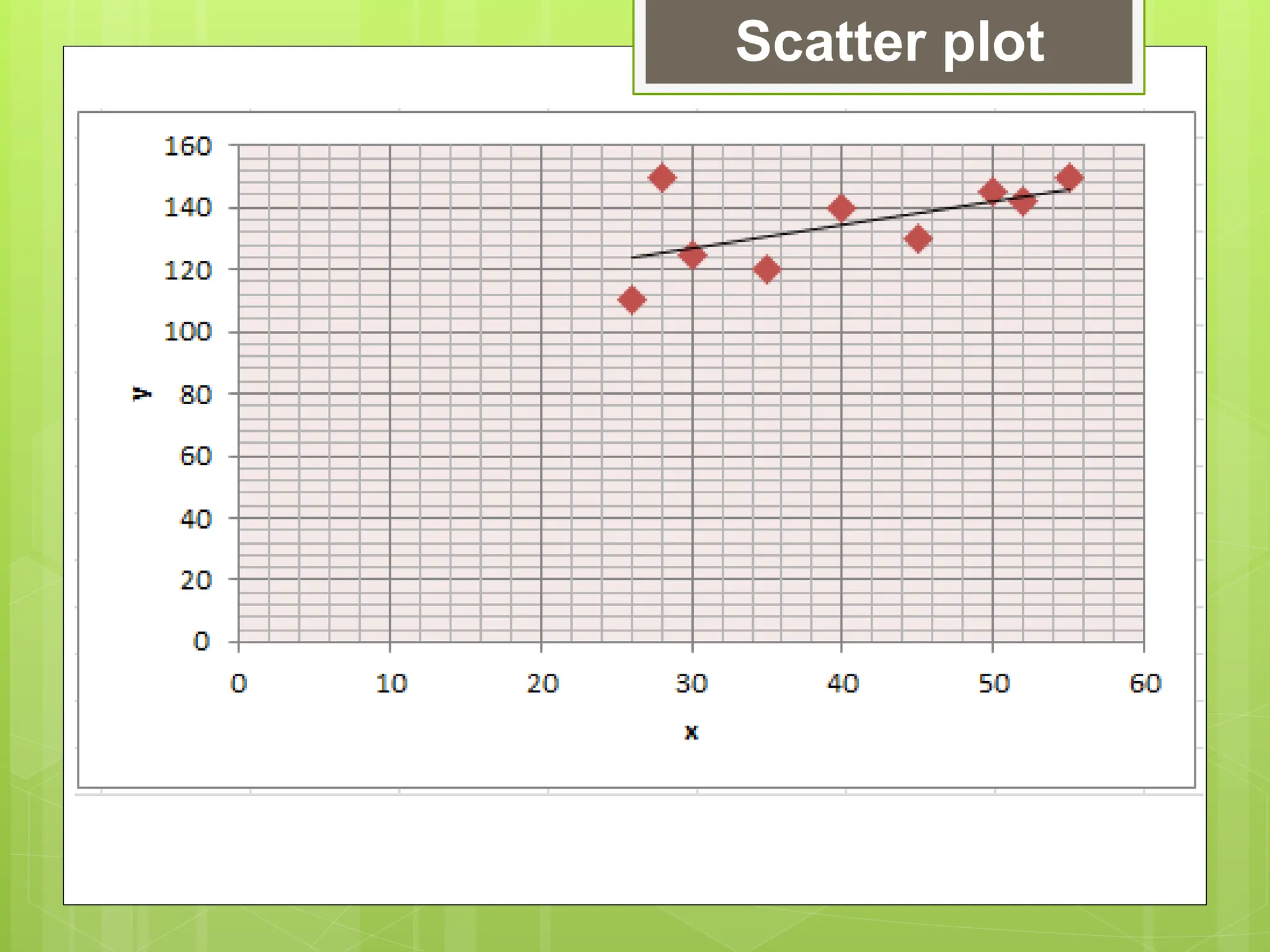
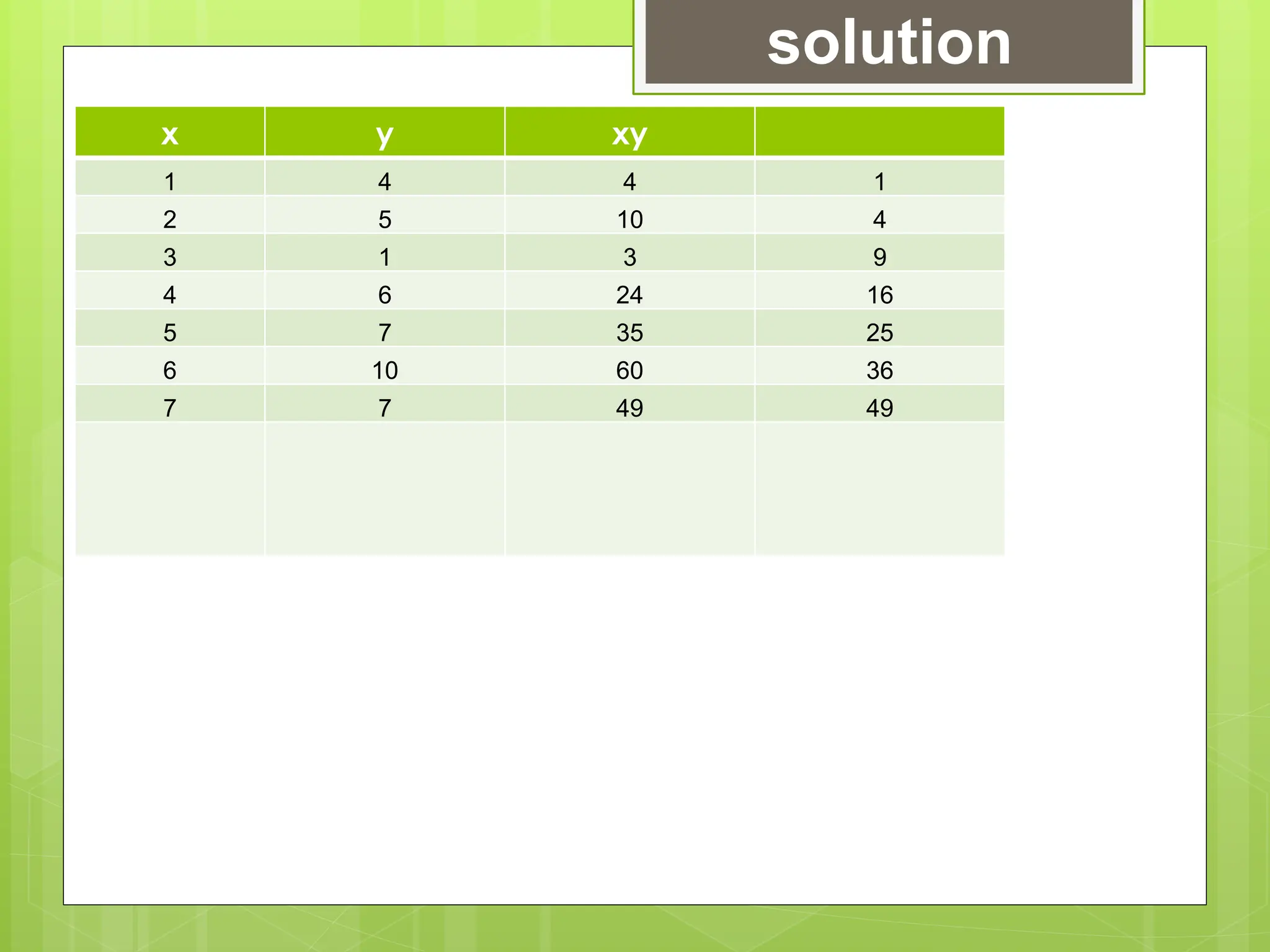
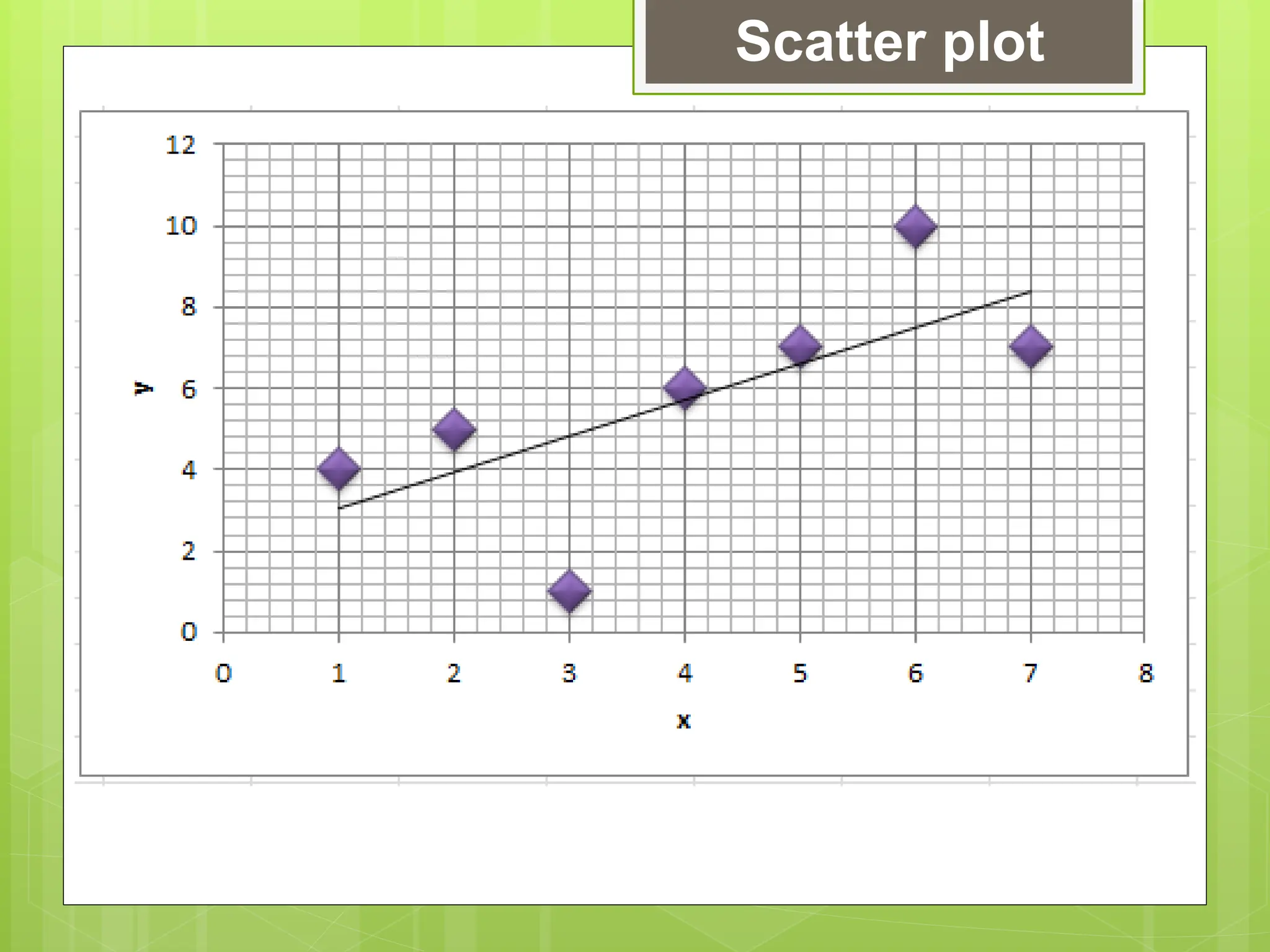
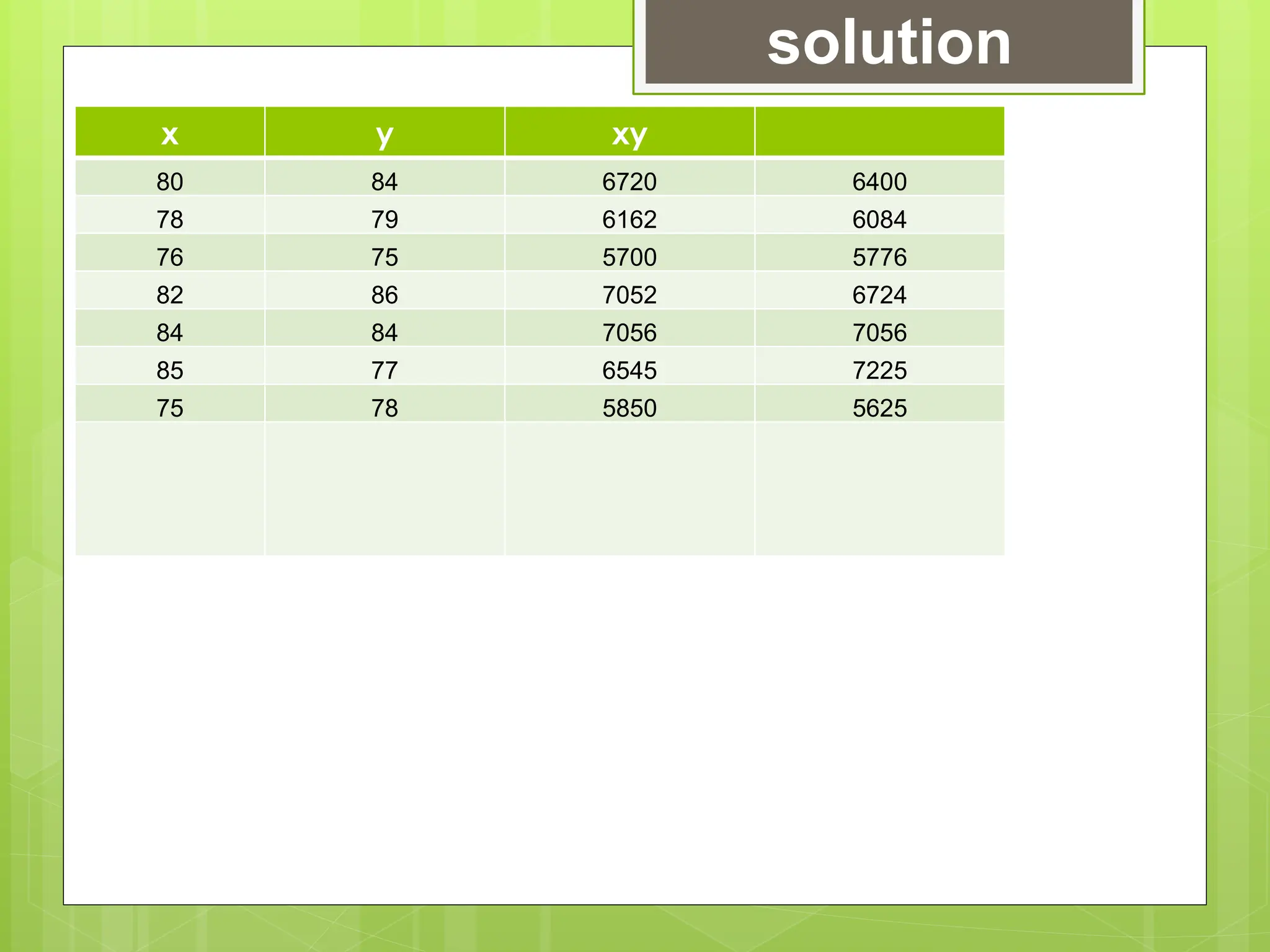
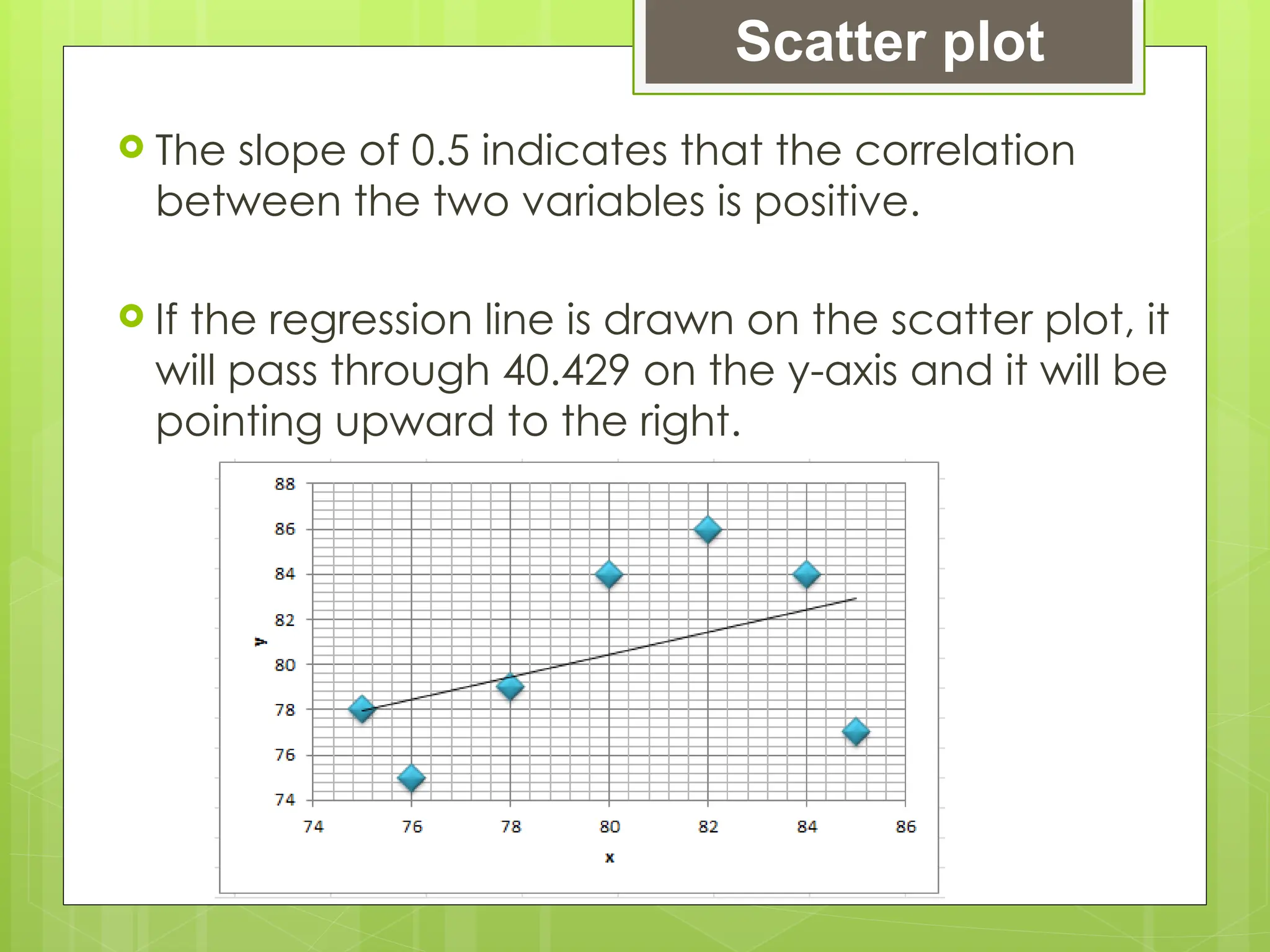
The document outlines the learning competencies for regression analysis, including identifying variables, drawing best-fit lines, calculating slopes and y-intercepts, and using regression equations for predictions. It provides step-by-step examples of constructing scatter plots, calculating equations of regression lines, and interpreting results with real-world data. The emphasis is on the importance of slope and y-intercept in determining relationships between variables.

1. REGRESSION
ANALYSIS

2. Learning Competencies
The learner will be able to:
1. Identify the independent and dependent variable;
2. Draw the best fit line on a scatter plot;
3. Calculate the slope and the y-intercept of the
regression line;
4. Interpret the calculated slope and the y-intercept
of the regression line;
5. Predict the value of the dependent variable given
the value of the independent variable; and
6. Solve problems involving regression analysis.

3.  Independent variable
 Dependent variable
The straight line that best illustrates the trend
or direction that the data points seem to
follow is called the best-fit line or line of the
best fit.
Steps:
1. Draw the line
2. Calculate slope and y-intercept
3. Find the equation of the line
Bivariate data in Scatter
plot

4. Consider the following data.
a. Construct a scatter plot.
b. Draw the line of best fit.
c. Calculate the slope and the y-intercept and then write the
equation of the line of best fit.
Solution
Example 1
x 1 2 3 4 5 6 7
y 4 3 8 6 12 10 8

5. c.
Step 1. Find the slope.
Use the points (1,4) and (6,10) which are on the line.
Step 2. Find the y-intercept.
Use the slope-intercept form of the equation of a
line and the point (1,4).

6. Step 3. Write the equation of the line of best fit.
Substitute the value of m and the value of b
in .
The equation of the line best fit is
or if the slope and the y-intercept are rounded
to nearest integer.

7.  However, if another student will use two points other
than those used in the above computations, he would
obtain a different equation for the line of best fit.
 The above computation is preferred if there is a perfect
correlation between variables, or the points lie on a
straight line.
 However, if the points are scattered or not on a straight
line, there is a better way to find the equation of the line
of best fit. This equation is called the equation of the
regression line or simply regression equation.

8. The equation of the regression line is
where
y-intercept of the regression line; and
slope of the regression line.
The y-intercept formula:
The slope formula:
Equation of Regression
Line

9. Consider the following data:
a. Find the equation of the regression line.
b. Draw the graph of the regression equation on a scatter plot
Solution
Example 2
x 1 2 3 4 5 6 7
y 4 3 8 6 12 10 8
x y xy
1 4 4 1
2 3 6 4
3 8 24 9
4 6 24 16
5 12 60 25
6 10 60 36
7 8 56 49

10. The equation of the regression line is
Solving and

11. Scatter plot

12. Find the regression equation using the following data:
Solution
Example 3
x 5 10 20 8 15 25
y 40 26 18 30 20 15
x y xy
5 40 200 25
10 26 260 100
20 18 360 400
8 30 240 64
15 20 300 225
25 15 375 625

13. The equation of the regression line is
Solving and

14. Scatter plot

15. Shown below are the ages (x) and the systolic blood pressure
numbers (y) of 9 male patients in a certain hospital. Find the
regression equation.
Solution
Example 4
Age (x) 26 40 35 50 45 55 28 30 52
Systolic Blood
pressure number
110 140 120 145 130 150 150 125 142

16. solution
Patient x y xy
1 26 110 2860 676
2 40 140 5600 1600
3 35 120 4200 1225
4 50 145 7250 2500
5 45 130 5850 2025
6 55 150 8250 3025
7 28 150 4200 784
8 30 125 3750 900
9 52 142 7384 2704

17. The equation of the regression line is
Solving and

18. Scatter plot

19. Prediction and
Estimation
Using the Regression
Equation for

20.  The regression equation can be used to predict or estimate the
value of the dependent variable if the value of the independent
variable is given.

21. Consider the following data:
a. Find the equation of the regression line.
b. Draw the graph of the regression equation on the scatter
plot.
c. Estimate the value of if
Example 5
x 1 2 3 4 5 6 7
y 4 5 1 6 7 10 7

22. solution
x y xy
1 4 4 1
2 5 10 4
3 1 3 9
4 6 24 16
5 7 35 25
6 10 60 36
7 7 49 49

23. The equation of the regression line is
Solving and

24. Scatter plot

25. Estimating the Value of y

26.  The slope and the y-intercept play important roles
in estimating or predicting the value of the
dependent variable.
 The amount of increase or decrease is indicated
by the slope of the regression equation.
 The slope also indicates whether the correlation
between the two variables is positive or negative.

27. The grades of 7 students in the first and second grading periods
are shown below.
a. Find the equation of the regression line.
b. Estimate the grade in the second grading period of a
student who received a grade of 88 in the first grading
period.
Example 6
x 80 78 76 82 84 85 75
y 84 79 75 86 84 77 78

28. solution
x y xy
80 84 6720 6400
78 79 6162 6084
76 75 5700 5776
82 86 7052 6724
84 84 7056 7056
85 77 6545 7225
75 78 5850 5625

29. The equation of the regression line is
Solving and

30. Scatter plot
 The slope of 0.5 indicates that the correlation
between the two variables is positive.
 If the regression line is drawn on the scatter plot, it
will pass through 40.429 on the y-axis and it will be
pointing upward to the right.

31. Estimating the Value of y