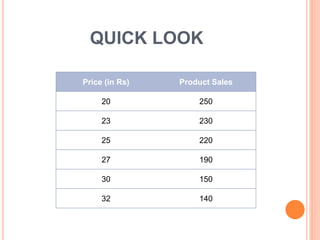
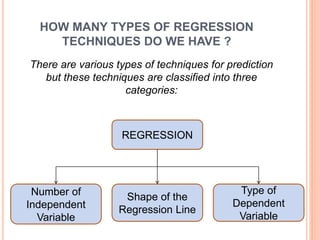
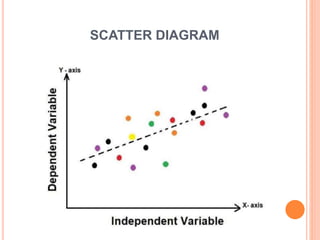
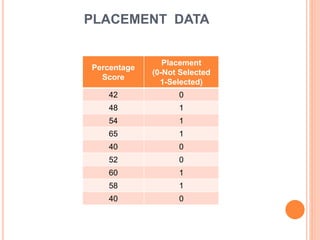
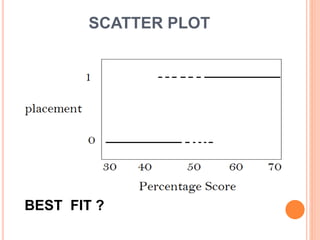
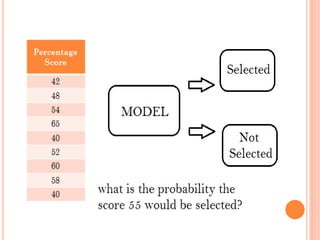
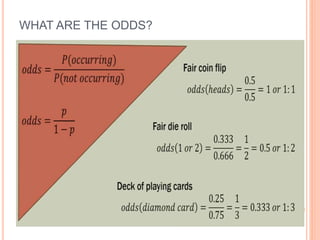
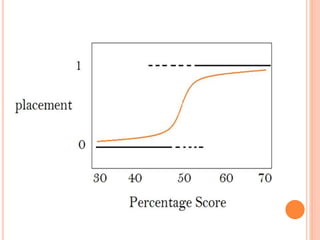
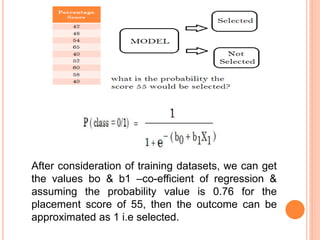
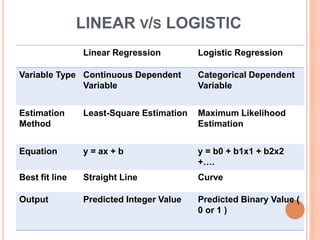
This document discusses regression analysis techniques. It defines regression as the tendency for estimated values to be close to actual values. Regression analysis investigates the relationship between variables, with the independent variable influencing the dependent variable. There are three main types of regression: linear regression which uses a linear equation to model the relationship between one independent and one dependent variable; logistic regression which predicts the probability of a binary outcome using multiple independent variables; and nonlinear regression which models any non-linear relationship between variables. The document provides examples of using linear and logistic regression and discusses their key assumptions and calculations.

1. REGRESSION
ANALYSIS
Prof. Sachin.S.L

2. QUICK LOOK
Price (in Rs) Product Sales
20 250
23 230
25 220
27 190
30 150
32 140

3. REGRESSION
The property of the tendency
of the actual value to lie close
to the estimated value.

4. REGRESSION ANALYSIS
It is a predictive modeling technique
which investigates & estimates
the relationship between the variables.
In the Regression Analysis,
 The independent variable is known also as
Regressor/Predictor/Explanatory variable.
 The dependent variable is known also as
Regressed/Predicted/Explained variable

5. WHY WE USE
REGRESSION ANALYSIS?
The main theme is to estimate the relationship
between two or more variables.
The benefits of using regression analysis:
 It indicates the Significant Relationships between
dependent and independent variable.
 It indicates the Strength of Impact of multiple
independent variables on a dependent variable.

6. HOW MANY TYPES OF
REGRESSION TECHNIQUES
DO WE HAVE
?

7. HOW MANY TYPES OF REGRESSION
TECHNIQUES DO WE HAVE ?
There are various types of techniques for prediction
but these techniques are classified into three
categories:
Number of
Independent
Variable
Shape of the
Regression Line
Type of
Dependent
Variable
REGRESSION

8. LINEAR REGRESSION
 The simplest mathematical relationship between
two variables such as one being independent and
other dependent
 The least square linear regression is a method for
predicting the value of a dependent variable Y,
based on the value of an independent variable X
using the linear equation.

9. LINEAR EQUATION
The Linear equation of two variables:
y = a x + b
Where,
y – dependent variable
x – independent variable
a – slope of the line
b – intercept (y-intercept)

10. SCATTER DIAGRAM

11. CALCULATION
The regression equation obtained with the assumption that x
–independent variable & y-dependent variable,
then regression equation given by:
Where, byx – regression co-efficient

12. EXAMPLE ?
Reference to Excel Spreadsheet

13. LOGISTIC
REGRESSION
?

14. LOGISTIC REGRESSION
It is a regression method used to find
the probability of an event which is a
binary outcome.
In other words,
It is a regression analysis to conduct
when the dependent variable is
dichotomous(binary).

15. EXAMPLE
How does the probability of placement
(Selected / Not-selected) change for
every additional percentage score in
examination?
Do change in body fat intake & age
have an influence on the probability of
having a heart attack (Yes / No)?

16. MAJOR ASSUMPTIONS &
UNDERSTANDINGS
 The dependent variable should be dichotomous in
nature (Ex: Pass/Fail, Present/Absent)
 There should be no high correlations (multi-
colinearity) among the predictors(independent
variables).
 It requires large sample size because maximum
likelihood estimates are less powerful at low
sample sizes.
 The regression doesn’t require linear relationship
between dependent and independent variables.

17. RANGE, ODDS & LOGIT FUNCTION
Here the value of Y-dependent variable ranges from
0 to 1 and it can be represented by following
equation

18. PLACEMENT DATA
Percentage
Score
Placement
(0-Not Selected
1-Selected)
42 0
48 1
54 1
65 1
40 0
52 0
60 1
58 1
40 0

19. SCATTER PLOT
BEST FIT ?

21. PROBABILITY

22. WHAT ARE THE ODDS?

23. ODDS RATIO

24. BRING BERNOULLI

26. PREDICTIVE EQUATION

28. After consideration of training datasets, we can get
the values bo & b1 –co-efficient of regression &
assuming the probability value is 0.76 for the
placement score of 55, then the outcome can be
approximated as 1 i.e selected.

29. LINEAR V/S LOGISTIC
Linear Regression Logistic Regression
Variable Type Continuous Dependent
Variable
Categorical Dependent
Variable
Estimation
Method
Least-Square Estimation Maximum Likelihood
Estimation
Equation y = ax + b y = b0 + b1x1 + b2x2
+….
Best fit line Straight Line Curve
Output Predicted Integer Value Predicted Binary Value (
0 or 1 )

30. THANK YOU