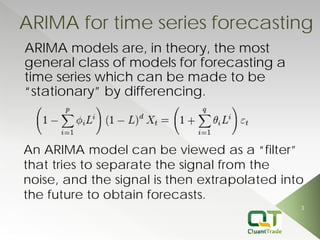
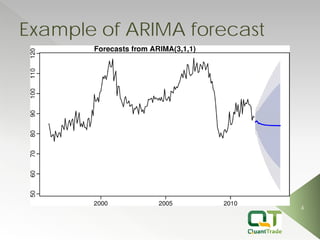
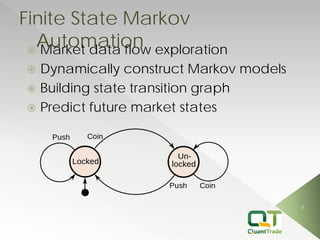
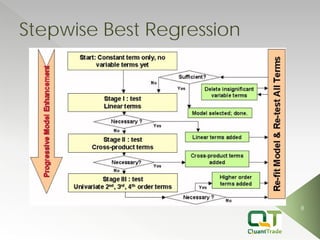
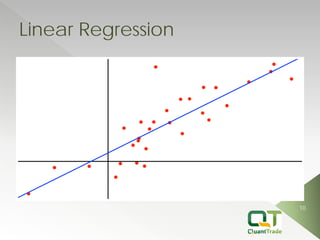
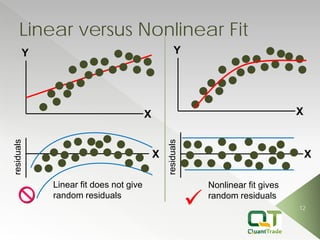
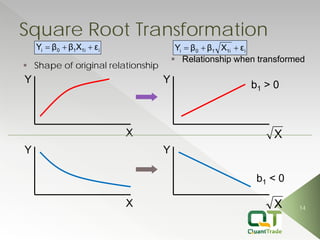
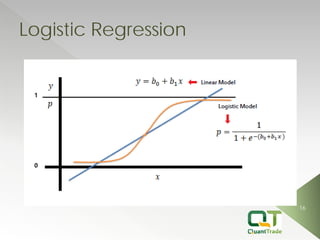
This document describes market forecasting algorithms provided by Quant Trade Technologies, including self-optimizing ARIMA, finite impulse response neural networks, finite state Markov automation, stepwise best regression, square root regression, logistic regression, and more. It explains the mathematical models behind various linear and nonlinear regression techniques for time series forecasting and analyzing financial market data.