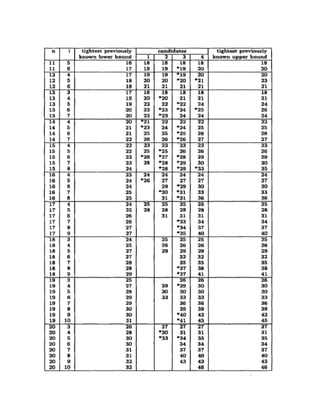
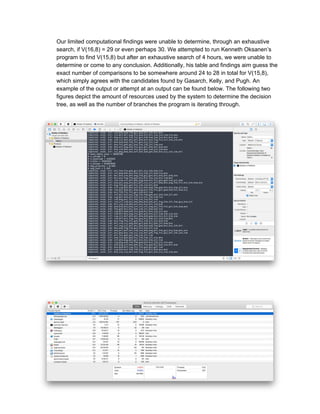
The document discusses algorithms for determining the median element in a set through pairwise comparisons. It examines Donald Knuth's decision tree approach for sets with up to 10 elements. An algorithm for finding the median of 7 elements through 10 comparisons is presented. The paper also reviews an ACM article providing a general algorithm for finding the ith element in a set of up to 20 elements. While the authors' computations did not determine the exact number of comparisons for sets larger than 15 elements, they confirm prior work establishing bounds for such problems.

1. Determining Median Complexity Through One­to­One Comparisons
Dragos Guta
Varatep Buranintu
David Wu
Michael Briseno
Combining the knowledge learned in class and the resources founded on the web, we were able
to come up with solutions as follows:
1. Determining a decision tree for V(7,4) where 7 refers to the number of elements in a set,
and 4 being the median or upper median. A general algorithm for determining the
number of comparisons is established by Donald Knuth, in The Art of Computer
Programming Volume 3 through trial and error.

2. Furthermore, Donald Knuth provides a table determining bounds for up to V(10,10).
Establishing a decision tree for V(7,4) ourselves is fruitless since a correct tree will
essentially mirror the one provided by Knuth.
Additionally the work of Kenneth Oksanen (​http://www.cs.hut.fi/~cessu/selection/​) has
established a table determining bounds possibly for up to V(15, 8).

3. 2. An algorithm for determining a height 10 decision tree for 7 elements boils down to
pairwise comparisons between the elements. A rudimentary implementation in
pseudocode is as follows:
//Createobjectthattakesinanint
//grabuserinputfor7integers
list2[]->1...7
secondround[]
forito7;i+2 (3c)
comparelist2[i]tolist2[i+1];
secondround.add(max(list2[i],list2[i+1]));
(Note:7thelementdoesnotgetcomparedtoanythingyet)
foritosecondround.size-1 (3c+2c=5c)
comparesecondround[0]tosecondround[i+1]
findmax
//deletemax
//ourlistsizeisnow6
objloner=list2[5];
placelonerinsidecellwhereourmaxwasat
secondround.add(max(loner,andunpairedvalue)); (​5c+1c=6c)
foritosecondround.size-1 (6c+2c=8c)
comparesecondround[0]tosecondround[i+1]
findmax
//deletemax
loner=theunpairedvaluethatismadeafterdeletingthemax
secondround.add(loner);
runnerup=newint;
foritosecondround.size-1 (8c+2c=10c)
comparesecondround[0]tosecondround[i+1]
findmaxandrunnerup
//deletemax
print(Runnerup.value+“isourmedian");
//printoutnumberofcomparisons

4. 3. A general algorithm for finding the median in a given set of 20 elements is provided by
William Gasarch, Wayne Kelly, and William Pugh in the paper Finding the ​i​th largest of ​n
for small ​i,n​ and is published through the Association for Computing Machinery (ACM).
Pseudocode for the implementation of their program is provided as such:
Additional information is provided in the paper such as an explanation of the notation
used. Furthermore, the paper provided establishes upper and lower bounds for up to 12
elements. The article further expands on the general algorithm and provides
“refinements” which expands to a value of ​n​ up to 20. Specifically for the case of V(16,8)
the previously known upper bound was 36, the above algorithm and refinements reduce
the bound to a potential candidate of 31, with a known lower bound of 25.

6. Our limited computational findings were unable to determine, through an exhaustive
search, if V(16,8) = 29 or even perhaps 30. We attempted to run Kenneth Oksanen’s
program to find V(15,8) but after an exhaustive search of 4 hours, we were unable to
determine or come to any conclusion. Additionally, his table and findings aim guess the
exact number of comparisons to be somewhere around 24 to 28 in total for V(15,8),
which simply agrees with the candidates found by Gasarch, Kelly, and Pugh. An
example of the output or attempt at an output can be found below. The following two
figures depict the amount of resources used by the system to determine the decision
tree, as well as the number of branches the program is iterating through.

7.
In conclusion, we were unable to determine V(16,8) = 29 or even 30. The amount of
resources and limited time as students was surely a hinderance to the project. We were
only able to confirm to the best of our abilities the work set forth previously by leaders in
the field such as Donald Knuth, Kenneth Oksanen, William Gasarch, Wayne Kelly, and
William Pugh. Additionally if we were to have made a discovery of that magnitude, to
state with confidence that V(16,8) = 29, then surely that would be worthy of an
academic, published and peer reviewed paper.