Dokument predstavlja nastavni materijal za učenje programiranja u C jeziku, uključujući osnove računarstva, strukturu programa i razne koncepcije kao što su pokazivači, nizovi i dinamičko alociranje memorije. Također obrađuje teme poput rekurzije, struktura podataka i algoritama, pružajući praktične primjere i zadatke za studente. Ivo Mateljan objasnio je važnost programskih jezika i računalnog osoblja u kontekstu suvremenih aplikacija i digitalnog obraza.

































![Programer, koji programira u višem programskom jeziku, ne mora znati kako se neki broj
kodira u procesoru ili memoriji računala. Njega zanimaju pravila za zapis literalnih konstanti,
veličina zauzeća memorije, maksimalna i minimalna vrijednost broja, te broj točnih decimala.
Normaliziranim zapisom postiže se točnost na 7 decimala za jednostruki format, odnosno 15
decimala za prošireni format.
4.1.4. Kodiranje znakova
Znak (eng. character) je element dogovorno usvojenog skupa različitih simbola koji su
namijenjeni obradi podataka (slova abecede, numeričke znamenke, znakovi interpunkcije i sl.).
Niz znakova se često tretira kao cjelina i naziva se string. Primjerice, u C jeziku se string
literalno zapisuje kao niz znakova omeđen znakom navodnika ("ovo je literalni zapis C
stringa").
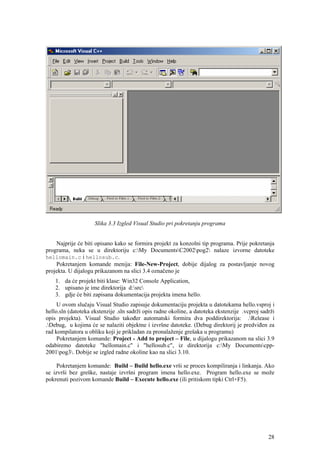
Za kodiranje slova, znamenki i ostalih tzv. kontrolnih znakova koristi se američki standard
za izmjenu informacija ASCII (American Standard Code for Information Interchange). Njemu
je ekvivalentan međunarodni standard ISO 7. ASCII kôd se najviše koristi za komuniciranje
između računala i priključenih vanjskih jedinica: pisača, crtača, modema, terminala itd.
To je sedam bitni kôd (ukupno 128 različitih znakova), od čega se prva 32 znaka koriste
kao kontrolni znakovi za različite namjene, a ostali znakovi predstavljaju slova abecede,
pravopisne i matematičke simbole.
000: (nul) 016: (dle) 032: (sp) 048: 0 064: @ 080: P 096: ž 112: p
001: (soh) 017: (dc1) 033: ! 049: 1 065: A 081: Q 097: a 113: q
002: (stx) 018: (dc2) 034: " 050: 2 066: B 082: R 098: b 114: r
003: (etx) 019: (dc3) 035: # 051: 3 067: C 083: S 099: c 115: s
004: (eot) 020: (dc4) 036: $ 052: 4 068: D 084: T 100: d 116: t
005: (enq) 021: (nak) 037: % 053: 5 069: E 085: U 101: e 117: u
006: (ack) 022: (syn) 038: & 054: 6 070: F 086: V 102: f 118: v
007: (bel) 023: (etb) 039: ' 055: 7 071: G 087: W 103: g 119: w
008: (bs) 024: (can) 040: ( 056: 8 072: H 088: X 104: h 120: x
009: (tab) 025: (em) 041: ) 057: 9 073: I 089: Y 105: i 121: y
010: (lf) 026: (eof) 042: * 058: : 074; J 090: Z 106: j 122: z
011: (vt) 027: (esc) 043: + 059: ; 075: K 091: [ 107: k 123: {
012: (np) 028: (fs) 044: , 060: < 076: L 092: 108: l 124: |
013: (cr) 029: (gs) 045: - 061: = 077: M 093: ] 109: m 125: }
014: (so) 030: (rs) 046: . 062: > 078: N 094: ^ 110: n 126: ~
015: (si) 031: (us) 047: / 063: ? 079: O 095: _ 111: o 127: del
Tablica 4.3. ACSII standard za kodiranje znakova
U Hrvatskoj se za latinična slova Č,Š,Ž,Ć i Đ koristi modifikacija ASCII standarda. (tablica
4.4).
HR-ASCII IBM EBCDIC-852 standard
dec hex ASCII HR-ASCII Dec hex EBCDIC-852
64 40 @ Ž 166 A6 Ž
91 5B [ Š 230 E6 Š
92 5C Đ 209 D1 Đ
93 5D ] Ć 172 AC Ć
94 5E ^ Č 143 8F Č
96 60 ` ž 167 A7 ž
123 7B { š 231 E7 š
124 7C | đ 208 D0 đ
125 7D } ć 134 86 ć
126 7E ~ č 159 9F č
Tablica 4.4. HR_ASCII i EBCDIC-852 standard
38](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-38-320.jpg)



![4.3 Prosti tipovi podataka
U uvodu je naglašeno da ime varijable simbolički označava položaj u memoriji (adresu) na
kojem je upisana vrijednost varijable. Sada ćemo uz pojam varijable uvesti i pojam tipa
varijable.
U matematici je uobičajeno uz matematičke izraze navesti i skup vrijednosti varijabli za
koje ti izrazi vrijede. Primjerice, neka varijabla x pripada skupu realnih brojeva (x ∈ R), a
varijabla z skupu kompleksnih brojeva (z ∈ Z). Tada vrijedi:
z Re( z) Im( z)
= + j
x x x
Vrijednost ovog izraza također pripada skupu kompleksnih brojeva. Bitno je uočiti da oznaka
pripadnosti skupu vrijednosti određuje način kako se računa matematički izraz i kojem skupu
vrijednosti pripada rezultat izraza. U programskim se jezicima pripadnost skupu koji ima
zajedničke karakteristike naziva tipom. Tip varijable određuje način kodiranja, veličinu
zauzimanja memorije i operacije koje su sa tom varijablom dozvoljene. Tipovi varijabli (ili
konstanti) koji se koriste u izrazima određuju tip kojim rezultira taj izraz.
U većini programskih jezika se koriste sljedeći tipovi podataka:
• numerički (cjelobrojni ili realni),
• logički,
• znakovni,
a nazivaju se i primitivni ili prosti tipovi jer predstavljaju nedjeljive objekte koji imaju izravan
prikaz u memoriji računala.
Tip Oznaka u Interval zauzeće
C jeziku vrijednosti Memorije
znakovni [signed] char -127 .. 128 1 bajt
tip Unsigned char 0 .. 255 1 bajt
cjelobrojni [signed] int -2147483648.. 2147483647 4 bajta
tip [signed] short -32768 .. 32767 2 bajta
[signed] long -2147483648.. 2147483647 4 bajta
kardinalni unsigned [int] 0 .. 4294967295 4 bajta
tip unsigned short 0 .. 65535 2 bajta
unsigned long 0 .. 4294967295 4 bajta
realni tip min ± 1.175494351e-38
(jednostruk float maks ± 3.402823466e+38 4 bajta
i format)
realni tip double min ± 2.2250738585072014e-308 8 bajta
(dvostruki maks ± 1.7976931348623158e+308
format)
logički tip - 0 .. različito od nule -
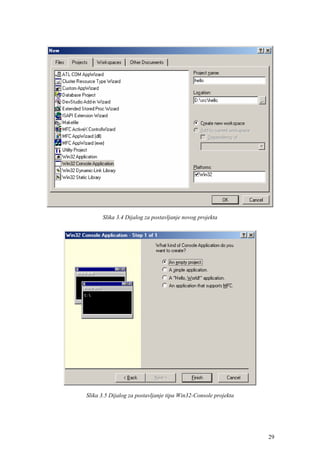
Tablica 4.6. Označavanje standardnih tipova podataka u C jeziku (uglate zagrade označavaju
opcioni element)
Tablica 4.6 prikazuje karakteristike standardnih tipove podataka koji se koriste u C jeziku;
ime kojim se označavaju, interval vrijednosti i veličina zauzeća memorije u bajtima. Uglate
zagrade označavaju opciona imena tipova, primjerice može se pisati
int ili signed int
unsigned ili unsigned int
42](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-42-320.jpg)




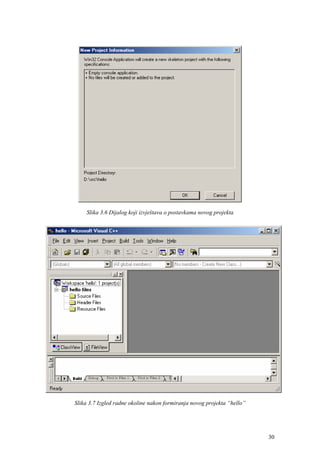
![Na kraju ovog poglavlja pogledajmo program Limits.c. Njime se ispisuje minimalna i
maksimalna vrijednost za sve proste tipove podataka C jezika. U programu se koriste
simboličke konstante koje su pomoću direktive #define zapisane u standardnim datotekama
limits.h i float.h.
/* Datoteka: Limits.c */
/* Ispisuje interval vrijednost numeričkih tipova */
#include <stdio.h>
#include <limits.h>
#include <float.h>
int main( void )
{
printf("%12s%12s%15s%15sn",
"Tip", "Sizeof", "Minimum", "Maksimum");
printf("%12s%15d%15dn","char", CHAR_MIN, CHAR_MAX) ;
printf("%12s%15d%15dn","short int", SHRT_MIN, SHRT_MAX) ;
printf("%12s%15d%15dn","int", INT_MIN, INT_MAX) ;
printf("%12s%15ld%15ldn","long int", LONG_MIN, LONG_MAX) ;
printf("%12s%15g%15gn", "float", FLT_MIN, FLT_MAX) ;
printf("%12s%15g%15gn", "double", DBL_MIN, DBL_MAX) ;
printf("%12s%15Lg%15Lgn","long double",LDBL_MIN, LDBL_MAX) ;
return 0 ;
}
Nakon izvršenja dobije se ispis:
Tip Sizeof Minimum Maksimum
char 1 -128 127
short int 2 -32768 32767
int 4 -2147483648 2147483647
long int 4 -2147483648 2147483647
float 4 1.17549e-038 3.40282e+038
double 8 2.22507e-308 1.79769e+308
long double 8 2.22507e-308 1.79769e+308
Ovaj ispis izgleda uredno. To je postignuto korištenjem specifikatora ispisa printf() funkcije
u proširenom obliku, tako da je između znaka % i oznake tipa ispisa upisan broj kojim se
određuje točan broj mjesta za ispis neke vrijednosti.
4.5 Specifikatori printf funkcije
Kada se ispis vrši po unaprijed određenom obliku i rasporedu kažemo da se vrši formatirani
ispis. Sada će biti pokazano kako se zadaje format ispisa printf() funkcije. Općenito format
se zadaje pomoću šest polja:
%[prefiks][širina_ispisa][. preciznost][veličina_tipa]tip_argumenta
Format mora započeti znakom % i završiti s oznakom tipa argumenta. Sva ostala polja su
opciona (zbog toga su napisana unutar uglatih zagrada).
U polje širina_ispisa zadaje se minimalni broj kolona predviđenih za ispis vrijednosti. Ako
ispis sadrži manji broj znakova od zadane širine ispisa, na prazna mjesta se ispisuje razmak.
Ako ispis sadrži veći broj znakova od zadane širine, ispis se proširuje. Ako se u ovo polje
47](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-47-320.jpg)












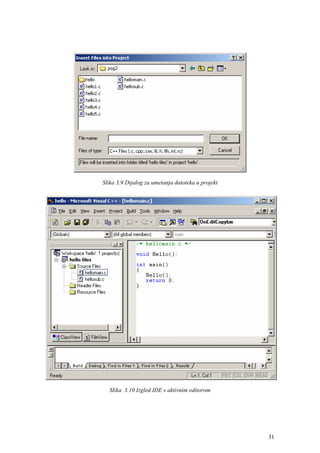
![5.2.2 Uvjetna naredba – if naredba
Nakon provedenog testiranja, pokazala se potreba za doradom prvog koraka algoritma
sljedećim operacijama:
Dorada koraka 1:
1. Dobaviti vrijednost od n.
1.1. Upozoriti korisnika da se očekuje unos broja unutar intervala [0,13]
1.2. Dobaviti otipkanu vrijednost u varijablu n
1.3 Ako je n < 0 ili n > 13 tada izvršiti sljedeće:
izvijestiti korisnika da je otkucao nedozvoljeni broj
prekinuti izvršenje programa
Kako implementirati ove korake u C jeziku? Korake 1.1 i 1.2 može se zapisati naredbama
printf("Unesite broj unutar intervala [0,13]n");
scanf("%d", &n);
Za implementaciju koraka 1.3 potrebno je upoznati kako se u C jeziku zapisuje uvjetna
naredba tzv. if-naredba. Njen opći oblik glasi:
if (izraz)
{
niz_naredbi ili if (izraz) naredba;
}
a značenje ove naredbe je: ako je (eng. if) izraz različit od nule izvršava se niz_naredbi koji je
omeđen vitičastim zagradama, u protivnom izvršit će se naredba koja slijedi iza if-naredbe.
Predikatni izraz, na temelju kojeg se u algoritamskom zapisu vrši selekcija, glasi:
n < 0 ili n > 13.
U C jeziku se logički operator “ili” zapisuje s dvije okomite crte ||, pa prethodni izraz u C
jeziku ima oblik
n < 0 || n > 13
(Napomena: logički operator “i” se zapisuje s &&, a logička negacija znakom ! ispred logičkog
izraza).
Sada se korak 1.3 može napisati u obliku:
if((n < 0) || (n > 13))
{
printf("Otipkali ste nedozvoljenu vrijednost");
return 1; /* forsirani izlaz iz funkcije main */
}
pa kompletni program izgleda ovako:
/* Datoteka fact2.c */
/* Proračun n!. Vrijednost od n unosi korisnik. */
/* Vrijednost od n mora biti unutar intervala [0,13]*/
#include <stdio.h>
int main()
61](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-61-320.jpg)
![{
int n, k, nfact;
printf("Unesite broj unutar intervala [0,13]n");
scanf("%d", &n);
if((n < 0) || (n > 13)) {
printf("Otipkali ste nedozvoljenu vrijednost");
return 1; /* forsirani izlaz iz funkcije main */
}
nfact = 1;
k = 1;
while ( k < n) {
k = k + 1;
nfact = k * nfact;
}
printf("Vrijednost %d! iznosi: %dn", n, nfact);
return 0;
}
Konačno je ostvaren kvalitetan i robustan program. On za bilo koju ulaznu vrijednost daje
rezultat nakon konačnog broja operacija. Ovo svojstvo se smatra temeljnim uvjetom koji mora
zadovoljiti svaki programski algoritam.
5.2.3 Naredba selekcije: if-else naredba
Radi vježbe i upoznavanja još jednog programskog iskaza – if-else naredbe, prethodni
algoritam se može zapisati u ekvivalentnom obliku:
Dobavi vrijednost od n.
Ako je n >= 0 i n<=13 tada
Izračunaj vrijednost n!.
Ispiši vrijednost od n i n!.
inače
Izvijesti o pogrešnom unosu
Kraj!
Tijek programa se sada kontrolira naredbom selekcije, koja ima značenje:
ako je logički uvjet istinit tada
izvrši prvi niz naredbi
inače
izvrši alternativni niz naredbi
U C jeziku se ovaj tip naredbe zove if-else naredba ili if-else iskaz, a zapisuje se prema obrascu:
if(izraz)
{
niz_naredbi1 ili if(izraz)
} naredba1;
else else
{ naredba2;
niz_naredbi2
}
62](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-62-320.jpg)
![Značenje ove naredbe u je: ako je (eng. if) izraz različit od nule izvršava se niz_naredbi1,
inače (eng. else) izvršava se niz_naredbi2. Ako niz_naredbi sadrži samo jednu naredbu ne
moraju se pisati vitičaste zagrade. Izraz se tretira kao logička vrijednost.
U ovom primjeru proračun n! će se izvršiti samo ako su istovremeno zadovoljena dva
uvjeta: n>=0 i n<=13. Ovaj se uvjet u C jeziku zapisuje s dva relacijska izraza povezana
logičkim operatorom “i”, koji se označava s &&.
Program sada izgleda ovako:
/* Datoteka fact3.c */
/* Proračun n!. Vrijednost od n unosi korisnik. */
/* Vrijednost od n mora biti unutar intervala [0,13]*/
#include <stdio.h>
int main()
{
int n, k, nfact;
printf("Unesite broj unutar intervala [0,13]n");
scanf("%d", &n);
if((n >= 0) && (n <= 13)) {
nfact = 1;
k = 1;
while ( k < n) {
k = k + 1;
nfact = k * nfact;
}
printf("Vrijednost %d! iznosi: %dn", n, nfact);
}
else
printf("Otipkali ste nedozvoljenu vrijednost");
return 0;
}
5.3 Funkcije C jezika
U prethodnoj su sekciji opisani temeljni iskazi kontrole izvršenja C programa, te kako se
oni koriste u implementaciji programskih algoritama. Čitav se program izvršavao unutar jedne
funkcije – main(). Unutar te funkcije korištene su standardne funkcije print() i scanf(),
iako nije poznato kako su te funkcije implementirane. Korištene su zbog toga jer su poznata
pravila njihove upotrebe i efekti koje one uzrokuju.
5.3.1 Korištenje funkcija iz standardne biblioteke C jezika
Funkcije se u programiranju koriste slično načinu kako se koriste funkcije u matematici.
Kada se u matematici napiše y=sin(x), x predstavlja argument funkcije, a ime funkcije sin
označava pravilo po kojem se skup vrijednosti, kojem pripada argument x, pretvara u skup
vrijednosti koje može poprimiti y.
Funkcija sin() se može koristiti i u izrazima C-jezika jer je implementirana u standardnoj
biblioteci funkcija. Primjerice, dio programa, u kojem se ona koristi, može biti sljedećeg
oblika:
#include <math.h>
int main()
63](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-63-320.jpg)



![je najbliži načinu kako optimizirajući kompilatori prevode prvi oblik funkcije kvadrat().
Danas mnogi programeri smatraju da uopće ne treba koristiti ključnu riječ register, jer
moderni optimizirajući kompilatori mnogo efikasnije koriste procesorske registre, nego što to
može učiniti programer tijekom procesa programiranja.
5.3.2 “void” funkcije
U programskim se jezicima često koristi dva tipa potprograma: funkcije i procedure.
Procedura je potprogram koji vrši neki proces, ali ne vraća nikakvu vrijednost. Pošto se u C-
jeziku svi potprogrami nazivaju funkcije, onda se kaže da je procedura funkcija koja vraća ništa
(eng. void). Primjerice, u trećem poglavlju korištena je funkcija void hello() za ispis
poruke "Hello World!".
Pomoću ključne riječi void označava se da je tip vrijednosti koji funkcija vraća "ništa",
odnosno da je nevažan. Poziv procedure se vrši njezinim imenom. Pošto procedure ne
vraćaju nikakvu vrijednost, ne mogu se koristiti u izrazima. U proceduri se ne navodi
ključna riječ return, iako se može koristiti (bez argumenta) ako se želi prekinuti
izvršenje procedure prije izvršenja svih naredbi koje se pozivaju u proceduri.
5.3.3 Primjer: funkcija za proračun n!
Za proračuna n-faktorijela zgodno je definirati funkciju koja obavlja taj proračun. Prototip
te funkcije može biti oblika:
int factorial(int n);
Funkcija factorial() će kao argument koristiti vrijednost tipa int. Primjena ove funkcije u
izrazima rezultirat će vrijednošću tipa int koji predstavlja vrijednost n-faktorijela. Definicija i
primjena funkcije zapisani su u programu fact4.c
/* Datoteka fact4.c */
/* Proračun n! pomoću funkcije factorial(n) */
/* Vrijednost od n mora biti unutar intervala [0,13]*/
#include <stdio.h>
/* definicija funkcije za proračun n faktorijela */
int factorial(int n)
{
int k = 1, nfact = 1;
while (k < n)
{
k = k + 1;
nfact = k * nfact;
}
return nfact;
}
int main()
{
int n;
printf("Unesite broj unutar intervala [0,13]n");
67](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-67-320.jpg)














![4. Operatori (+,-*/,..=, []..(), &, .+=,*=.) služe označavanju aritmetičko-logičkih i drugih
operacija koje se provode sa memorijskim objektima (funkcije i varijable) i konstantama.
5. Leksički separatori su znakovi koji odvajaju lekseme. Jedan ili više znakova razmaka,
tabulatora i kraja retka tretiraju se kao prazno mjesto, kojim se razdvajaju leksemi.
Operatori, također, imaju značaj leksičkih separatora. Znak točka-zarez (';') predstavlja
specijalni separator koji se naziva terminator naredbi.
6. Komentar se piše kao proizvoljni tekst. Početak komentara se označava znakovima /*, a
kraj komentara s */. Komentar se može pisati u bilo kojem dijelu programa, i u više linija
teksta. Mnogi kompilatori kao komentar tretiraju i tekst koji se unosi iza dvostruke kose crte
//, sve do kraja retka.
7. Specijalne leksičke direktive su označene znakom # na početku retka. Izvršavaju se prije
procesa kompiliranja, pa se nazivaju i pretprocesorske direktive. Primjerice, #include
<stdio.h> je pretprocesorska direktiva kojom se određuje da se u proces kompiliranja
uvrsti sadržaj datoteke imena stdio.h.
Kao što se zapis u prirodnom jeziku sastoji od različitih elemenata (subjekt, predikat, pridjev,
rečenica, poglavlje itd.), tako se i zapis u programskom jeziku sastoji od temeljnih elemenata,
koje prikazuje tablica 6.2.
Elementi programa Značenje Primjer
Tipovi oznake za skup vrijednosti int , float ,
s definiranim operacijama char
Konstante literalni zapis vrijednosti 0 , 123.6 ,
osnovnih tipova "Hello"
Varijable imenovane memorijskih lokacije koje i , sum
sadrže vrijednosti nekog tipa
Izrazi zapis proračuna vrijednosti kombiniranjem sum + i
varijabli, funkcija, konstanti i operatora
Naredbe ili iskazi zapisi pridjele vrijednosti, poziva funkcije i sum = sum + i;
kontrole toka programa while (--i)
if(!x).. else ..;
Funkcije imenovano grupiranje naredbi main()
(potprogrami) printf(...)
Kompilacijska skup međuovisnih varijabli i funkcija koji datoteka.c
jedinica se kompilira kao jedinstvena cjelina
Tablica 6.2 Temeljni elementi zapisa programa u C jeziku
Navedeni elementi jezika se iskazuju kombinacijom leksema prema strogim gramatičkim,
odnosno sintaktičkim pravilima, koji imaju nedvosmisleno značenje.
U prirodnim jezicima iskazi mogu imati više značenja, ovisno o razmještaju riječi, o
morfologiji (tvorba riječi) i fonetskom naglasku. U programskim jezicima se ne koristi
morfološka i fonetska komponenta jezika, pa se gramatika svodi na sintaksu, također, dozvoljen
je samo onaj raspored riječi koji daje nedvosmisleno značenje. Uobičajeno se kaže da gramatika
programskih jezika spada u klasu bezkontesktne gramatike.
82](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-82-320.jpg)



















![8 Nizovi
Naglasci:
• jednodimenzionalni nizovi
• inicijalizacija nizova
• višedimenzionalni nizovi
• prijenos nizova u funkcije
U ovom je poglavlju opisano kako se formiraju i koriste nizovi. Rad s nizovima je
"prirodni" način korištenja računala, jer memorija računala nije ništa drugo nego niz bajta. U
programiranju, kao i u matematici, zanimaju nas nizovi kao kolekcija istovrsnih elemenata koji
su poredani jedan za drugim.
Elementi niza su varijable koje se označavaju indeksom:
ai označava i-ti element niza u matematici
a[i] označava i-ti element niza u C jeziku i=0,1,2....
8.1 Jednodimenzionalni nizovi
8.1.1 Definiranje nizova
Niz je imenovana i numerirana kolekcija istovrsnih objekata koji se nazivaju elementi niza.
Elementi niza mogu biti prosti skalarni tipovi i korisnički definirani tipovi podataka.
Označavaju se imenom niza i cjelobrojnom izrazom – indeksom – koji označava poziciju
elementa u nizu. Indeks niza se zapisuje u uglatim zagradama iza imena niza. Primjerice, x[3]
označava element niza x indeksa 3.
Sintaksa zapisa elementa jednodimenzionalnog niza je
element_niza: ime_niza [ indeks ]
indeks: izraz_cjelobrojnog_tipa
Prvi element niza ima indeks 0, a n-ti element ima indeks n-1. Prema tome, x[3] označava
četvrti element niza.
S elementima niza se manipulira kao s običnim skalarnim varijablama, uz uvjet da je
prethodno deklariran tip elemenata niza. Sintaksa deklaracije jednodimenzionalnog niza je:
deklaracija_niza:
oznaka_tipa ime_niza [ konstantni_izraz ] ;
Primjerice, deklaracijom
int A[9];
definira se A kao niz od 9 elementa tipa int.
102](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-102-320.jpg)
![Deklaracijom niza rezervira se potrebna memorija, na način da Memorijski raspored
niza A
elementi niza zauzimaju sukcesivne lokacije u memoriji.
Vrijedi pravilo: adresa sadržaj
adresa(A)=adresa(A[0]) 1000 data[0]
1004 data[1]
adresa(A[n])=adresa(A[0]) + n*sizeof(A[0])) 1008 data[2]
1012 data[3]
Elementima niza se pristupa pomoću cjelobrojnog indeksa, 1016 data[4]
primjerice: 1020 data[6]
1024 data[5]
A[0] = 7; 1028 data[7]
int i=5; 1032 data[8]
A[2]= A[i];
for(i=0; i<9; i++) Napomena: int zauzima
printf("%d ", A[i]; 4 bajta
U C jeziku se ne vrši provjera da li je vrijednost indeksnog izraza unutar deklariranog
intervala. Primjerice, iskaz:
A[12] = 5;
je sintaktički ispravan i kompilator neće dojaviti grešku. Međutim, nakon izvršenja ove naredbe
može doći do greške u izvršenju programa, ili čak do pada operativnog sustava. Radi se o tome
da se ovom naredbom zapisuje vrijednost 5 na memorijsku lokaciju za koju nije rezervirano
mjesto u deklaraciji niza.
Primjer: U programu niz.c pokazano je kako se niz koristi za prihvat veće količine podataka -
realnih brojeva. Zatim, pokazano je kako se određuje suma elemenata niza te vrijednost i indeks
elementa koji ima najveću vrijednost.
/* Datoteka: niz1.c */
#include <stdio.h>
#define N 5
int main()
{
int i, imax;
double suma, max;
double A[N]; /* niz od N elemenata */
/* 1. izvjesti korisnika da otkuca 5 realnih brojeva */
printf("Otkucaj %d realnih brojeva:n", N);
for (i=0; i<N; i++)
scanf("%lg", &A[i]);
/* 2. izračunaj sumu elemenata niza */
suma = 0;
for (i=0; i<N; i++)
103](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-103-320.jpg)
![suma += A[i];
printf("Suma unesenih brojeva je %fn", suma);
/*3.odredi indeks(imax) i vrijednost(max) najvećeg elementa */
imax = 0;
max = A[0];
for(i=1; i<N; i++) {
if(A[i] > max ) {
max = A[i];
imax=i;
}
}
printf ("%d. element je najveci (vrijednost mu je %f)n",
imax+1, max);
return 0;
}
Izvršenje programa može izgledati ovako:
Otkucaj 5 realnih brojeva:
5 6.78 7.1 8 0.17
Suma unesenih brojeva je 27.050000
4. element je najveci (vrijednost mu je 8.000000)
8.1.2 Inicijalizacija nizova
Za globalno i statičko deklarirane nizove automatski se svi elementi postavljaju na
vrijednost nula. Kod lokalo deklariranih nizova ne vrši se inicijalizacija početnih vrijednosti
elemenata niza. To mora obaviti programer. Za inicijalizaciju elemenata niza na neku vrijednost
često se koristi for petlja, primjerice naredba
for (i = 0; i < 10; i++)
A[i] = 1;
sve elemente niza A postavlja na vrijednost 1.
Niz se može inicijalizirati i s deklaracijom sljedećeg tipa:
int A[9]= {1,2,23,4,32,5,7,9,6};
Lista konstanti, napisana unutar vitičastih zagrada, redom određuje početnu vrijednost
elemenata niza.
Ako se inicijaliziraju svi potrebni elementi niza, tada nije nužno u deklaraciji navesti dimenziju
niza. Primjerice,
int A[]= {1,2,23,4,32,5,7,9,6};
je potpuno ekvivalentno prethodnoj deklaraciji. Broj elemenata ovakvog niza uvijek se može
odrediti pomoću iskaza:
int brojelemenata = sizeof(A)/sizeof(int);
Niz se može i parcijalno inicijalizirati. U deklaraciji
int A[10]= {1,2,23};
104](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-104-320.jpg)
![prva tri elementa imaju vrijednost 1, 2 i 23, a ostale elemente prevodilac postavlja na vrijednost
nula.
Kada se inicijalizira znakovni niz, tada se u listi inicijalizacije mogu navesti znakovne
konstante:
char znakovi[2]= {'O','K'};
Primjer: U programu hex.c korisnik unosi cijeli broj bez predznaka, zatim se vrši ispis broja u
heksadecimalnoj notaciji.
/* Datoteka: hex.c
* ispisuje broj, kojeg unosi korisnik, u heksadecimalnoj notaciji
*/
#include <stdio.h>
int main()
{
int num, k;
unsigned broj;
char hexslova []= {'0', '1', '2', '3', '4', '5', '6', '7',
'8', '9', 'A', 'B', 'C', 'D', 'E', 'F'} ;
char reverse[8] = {0}; /* zapis do 8 heksa znamenki u reverznom
redu */
printf("Otkucaj cijeli broj bez predznaka: ");
scanf("%u", &broj);
if(broj <0) broj = -broj;
printf("Heksadecimalni zapis je: ");
num=0;
do {
k = broj % 16; /* iznos heksa znamenke */
reverse[num++] = hexslova[k]; /* oznaka heksa znamenke */
broj /= 16; /* odstrani ovu znamenku */
} while(broj != 0);
/* num sadrži broj heksa znamenki */
/* ispis od krajnjeg (n-1) do nultog znaka */
for(k=num-1; k>=0; k--)
printf("%c", reverse[k]);
printf("n");
return 0;
}
Pri izvršenju programa ispis može biti:
Otkucaj cijeli broj bez predznaka: 256001
Heksadecimalni zapis je: 3E801
Algoritam pretvorbe u heksadecimalnu notaciju je jednostavan. Temelji se na činjenici da
ostatak dijeljenja s 16 daje numeričku vrijednost heksadecimalne znamenke na mjestu
najmanjeg značaja. Ta se vrijednost (k=0..15) korisi kao indeks znakovnog niza
105](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-105-320.jpg)
![hexslova[k]. Vrijednost hexslova[k] je znak odgovarajuće heksadecimalne znamenke,
kojeg se pridjeljuje nizu reverse[] ( u njemu će na kraju biti zapisana heksadecimalna
notacija broja, ali obrnutm redoslijedom). Zatim se broj dijeli s 16 i dobavlja sljedeća
heksadecimalna znamenka. Taj se proces ponavlja sve dok je rezultat dijeljenja različit od nule.
Ispis broja u heksadecimalnoj notaciji se vrši tako da se ispiše sadržaj znakovnog niza reverzno,
počevši od znamenke najvećeg značaja, završno s znamenkom najmanjeg značaja (koja se u tom
nizu nalazi na indeksu 0).
Primjer: Histogram
U datoteci "ocjene.dat", u tekstualnom obliku, zapisane su ocjene u rasponu od 1 do 10.
Sadržaj datoteke "ocjene.dat” neka čini sljedeći niz ocjena:
2 3 4 5 6 7 2 4 7 8 9 1 3 4 6 9 8 7 2 5 6 7 8 9
3 4 5 1 7 3 4 10 10 9 10 5 7 6 3 8 9 4 5 7 3 4 6 1
2 9 6 7 8 5 4 6 3 2 4 5 6 1 3 4 6 9 10 7 2 10 7 8 1
Zadatak je izraditi program imena hist.c pomoću kojeg se prikazuje histogram ocjena u
10 grupa (1, 2,.. 10), i srednja vrijednost svih ocjena. Podaci iz datoteke "ocjene.dat" se predaju
programu "hist.exe" preusmjeravanjem standardnog ulaza (tipkovnice) na datoteku "ocjene dat".
To se vrši iz komandne linije komandom:
c:mydir> hist < ocjena.dat.
Na ovaj način se pristupa sadržaju datoteke kao da je otkucan s tipkovnice.
/* Datoteka: hist.c */
#include <stdio.h>
int main(void)
{
int i, ocjena, suma;
int izbroj[11] = {0}; /* niz brojača ocjena */
/* izbroj[0] sadrži ukupan broj ocjena
* izbroj[i] sadrži podatak koliko ima ocjena veličine i.
* Početno, elementi niza imaju vrijednost 0
*/
while (scanf("%d", &ocjena) != EOF)
{
izbroj[ocjena]++; /* inkrementiraj brojač ocjena */
izbroj[0]++; /* inkrementiraj brojač broja ocjena */
}
printf("Ukupan broj ocjena je %dn", izbroj[0]);
/* ispiši histogram - od veće prema manjoj ocjeni*/
for (i = 10; i > 0; i--)
{
int n = izbroj[i]; /* n je ukupan broj ocjena iznosa i */
printf("%3d ", i); /* ispiši ocjenu, a zatim */
while (n-- > 0) /* ispiši n zvjezdica */
printf("*");
printf("n");
106](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-106-320.jpg)
![}
/* izračunaj sumu svih ocjena */
suma =0;
for (i = 1; i < 11; i++)
suma += izbroj[i]*i;
/*ispiši srednju ocjenu */
printf ("Srednja ocjena je %4.2fn", (float)suma / izbroj[0]);
return 0;
}
Program se poziva komandom:
c:>hist < ocjene.dat
Dobije se ispis:
Ukupan broj ocjena je 73
10 *****
9 *******
8 ******
7 **********
6 *********
5 *******
4 **********
3 ********
2 ******
1 *****
Srednja ocjena je 5.79
Analiza programa hist.c:
Prvo je deklariran niz izbroj od 11 elemenata tipa int, a inicijaliziran je na vrijednost 0.
Program će u tome nizu bilježiti koliki je broj ocjena neke vrijednosti (izbroj[1] će
sadržavati broj ocjena veličine 1, izbroj[2] će sadržavati broj ocjena veličine 2, itd., a
izbroj[0] sadrži ukupan broj ocjena).
Bilježenje pojavnosti neke ocjene se dobije inkrementiranjem brojača izbroj[ocjena].
Ocjene se dobavljaju preusmjerenjem datoteke na standardni ulaz. Za unos pojedine ocjene
koristi se scanf() funkcija sve dok se na ulazu ne pojavi znak EOF (end-of-file), koji znači
kraj datoteke. Nakon toga se ispisuje histogram na način da se uz oznaku ocjene ispiše onoliko
zvjezdica koliko je puta ta ocjena zabilježena u nizu brojača ocjena.
Na kraju se računa srednja vrijednost ocjena na način da se suma svih ocjena podijeli s
ukupnim brojem ocjena. Uočite da je u naredbi
printf ("Srednja ocjena je %4.2fn", (float)suma / izbroj[0]);
izvršena eksplicitna pretvorba tipa operatorom (float), jer srednja vrijednost može biti realni
broj.
8.2 Prijenos nizova u funkciju
Nizovi mogu biti argumeti funkcije. Pri deklaraciji ili definiranju funkcije formalni
argument, koji je tipa niza, označava se na način da se deklarira niz bez oznake veličine niza, tj.
u obliku
107](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-107-320.jpg)
![tip ime_niza[]
Pri pozivu funkcije, kao stvarni argument, navodi se samo ime niza bez uglatih zagrada.
Primjer: u programu prod.c korisnik unosi niz od N realnih brojeva. Nakon toga, program
računa produkt svih elemenata niza, pomoću funkcije produkt(), i ispisuje rezultat.
/* Datoteka: prod.c */
/* Računa produkt elemenata niza od 5 elemenata */
#include <stdio.h>
#define N 5 /* radi s nizom od N elemenata */
double produkt(double A[], int brojelemenata)
{
int i;
double prod = 1;
for (i=0; i<brojelemenata; i++)
prod *= A[i];
return prod;
}
int main()
{
int i;
double A [N];
/* 1. izvjesti korisnika da otkuca 5 realnih brojeva */
printf("Otkucaj %d realnih brojeva:n", N);
for (i=0; i<N; i++)
scanf("%lg", &A[i]);
/* 2. izračunaj sumu elemenata niza */
printf("Suma unesenih brojeva je %gn", produkt(A, N));
return 0;
}
Uočite de se vrijednost elemenata niza može mijenjati unutar funkcije. Očito je da se niz ne
prenosi po vrijednosti (by value), jer tada to ne bi bilo moguće.
Pravilo je: U C jeziku se nizovi – i to samo nizovi – u funkciju prenose kao
memorijske reference (by reference), odnosno prenosi se adresa početnog elementa
niza. Brigu o tome vodi prevodilac. Memorijska referenca (adresa) varijable se
pamti "u njenom imenu" stoga se pri pozivu funkcije navodi samo ime, bez uglatih
zagrada.
Nizovi, koji su argumenti funkcije, ne smiju se unutar funkcije tretirati kao lokalne
varijable. Promjenom vrijednosti elementa niza unutar funkcije ujedno se mijenja
vrijednost elementa niza koji je u pozivnom programu označen kao stvarni
argument funkcije.
108](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-108-320.jpg)
![Primjer: Prijašnji primjer programa za histogram ocjena bit će modificiran, na način da se
definira tri funkcije: pojavnost ocjena u nizu izbroj bilježit će se funkcijom registriraj(), crtanje
histograma vršit će funkcija histogram(), a proračun srednje vrijednosti vršit će funkcija
srednja_ocjena().
/* Datoteka: histf.c */
#include <stdio.h>
void registriraj( int ocjena, int izbroj[])
{
izbroj[ocjena]++;
izbroj[0]++;
}
void histogram(int izbroj[])
{
int n,i;
for (i = 10; i > 0; i--) {
printf("%3d ", i);
n=izbroj[i];
while (n-- > 0)
printf("*");
printf("n");
}
}
float srednja_ocjena(int izbroj[])
{
/* izračunaj sumu svih ocjena */
int i, suma =0;
for (i = 1; i <= 10; i++)
suma += izbroj[i]*i;
return (float)suma / izbroj[0];
}
int main(void)
{
int i, ocjena, suma;
int izbroj[11]={0};
while (scanf("%d", &ocjena) != EOF)
registriraj(ocjena, izbroj);
histogram(izbroj);
printf ("Srednja ocjena je %4.2fn",srednjaocjena(izbroj));
return 0;
}
Primjer: Često je potrebno odrediti da li u nekom nizu od N elemenata postoji element
vrijednosti x. U tu svrhu zgodno je definirati funkciju
int search(int A[], int N, int x);
koja vraća indeks elementa niza A koji ima vrijednost x. Ako ni jedan element nema vrijednost
x, funkcija vraća negativnu vrijednost -1. Implementacija funkcije je:
int search (int A[], int N, int x)
{
109](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-109-320.jpg)
![int indx;
for(indx = 0; indx < N; indx++) {
if( A[indx] == x) /* element pronađen – prekini */
break;
}
if(indx == N) /* tada ni jedan element nema vrijednost x*/
return -1;
else
return indx;
}
Uočite, ako u nizu postoji više elemenata koji imaju vrijednost x, vraća se indeks prvog
pronađenog elementa.
8.3 Višedimenzionalni nizovi
Višedimenzionalnim nizovima se pristupa preko dva ili više indeksa. Primjerice,
deklaracijom:
int x[3][4];
definira se dvodimenzionalni niz koji ima 3 x 4 = 12 elemenata. Deklaraciju se može čitati i
ovako: definiran je niz kojem su elementi 3 niza s 4 elementa tipa int.
Dvodimenzionalni nizovi se često koriste za rad s Memorijski raspored niza
matricama. U tom slučaju nije potrebno razmišljati o adresa sadržaj
tome kako je niz složen u memoriji, jer se elementima
1000 x[ 0][ 0]
pristupa preko dva indeksa: prvi je oznaka retka, a 1004 x[ 0][ 1]
drugi je oznaka stupca matrice. 1008 x[ 0][ 2]
1012 x[ 0][ 3]
Matrični prikaz niza je: 1016 x[ 1][ 0]
x[0][0] x[0][1] x[0][2] x[0][3] 1020 x[ 1][ 1]
x[1][0] x[1][1] x[1][2] x[1][3] 1024 x[ 1][ 2]
x[2][0] x[2][1] x[2][2] x[2][3] 1028 x[ 1][ 3]
1032 x[ 2][ 0]
1036 x[ 2][ 1]
1040 x[ 2][ 2]
Memorijski raspored elemenata dvodimenzionalnog 1044 x[ 2][ 3]
niza, koji opisuju neku matricu, je takovi da su
elementi složeni po redovima matrice; najprije prvi
redak, zatim drugi, itd..
Višedimenzionalni niz se može inicijalizirani već u samoj deklaraciji, primjerice
int x[3][4] = { { 1, 21, 14, 8},
{12, 7, 41, 2},
{ 1, 2, 4, 3} };
Navođenje unutarnjih vitičastih zagrada je opciono, pa se može pisati i sljedeća deklaracija:
int x[3][4] = {1, 21, 14, 8, 12, 7, 41, 2, 1, 2, 4, 3};
Ovaj drugi način inicijalizacije se ne preporučuje, jer je teže uočiti raspored elemenata po
redovima i stupcima.
110](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-110-320.jpg)
![Elementima se pristupa preko indeksa niza. U sljedećem primjeru računa se suma svih
elemenata matrice x;
int i, j, brojredaka=3, brojstupaca=4;
int sum=0;
for (i = 0; i < brojredaka; i++)
for (j = 0; i < brojstupaca; j++)
sum += x[i][j];
printf("suma elemenata matrice = %d", sum);
Prijenos višedimenzionalnih nizova u funkciju
Kod deklariranja parametara funkcije, koji su višedimenzionalni nizovi pravilo je da se ne
navodi prva dimenzija (kao i kod jednodimenzionalnih nizova), ali ostale dimenzije treba
deklarirati, kako bi program prevodilac "znao" kojim su redom elementi složeni u memoriji.
Primjer: Definirana je funkcija sum_mat_el() kojom se računa suma elemenata
dvodimenzionalne matrice, koja ima 4 stupca:
int sum_mat_el(int x[][4], int brojredaka)
{
int i, j, sum=0;
for (i = 0; i < brojredaka; i++)
for (j = 0; i < 4; j++)
sum += x[i][j];
return sum;
}
Uočite da je u definiciji funkcije naveden i argument koji opisuju broj redaka matrice. Broj
stupaca je fiksiran već u deklaraciji niza na vrijednost 4. Očito da ova funkcija ima ograničenu
upotrebu jer se može primijeniti samo na matrice koje imaju 4 stupca. Kasnije, pri
proučavanju upotrebe pokazivačkih varijabli, bit će pokazano kako se ova funkcija može
modificirati tako da vrijedi za matrice proizvoljnih dimenzija.
111](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-111-320.jpg)









![char kvadrat[3][3];
Pojedini element matrice može poprimiti samo tri vrijednosti: ' ', 'X' i 'o' (prazno, križić i
točkica).
Za označavanje igrača koristit će se dvije globalne varijable
char racunalo, covjek;
prva će sadržavati znak koji unosi računalo, a druga znak koji unosi čovjek. Ako jedna od ovih
varijabli, primjerice covjek, ima vrijednost 'X', to znači da prvi potez vuče čovjek, inače, prvi
potez vuče računalo.
Na temelju početnog algoritma može se zaključiti da se problem može realizirati pomoću 5
neovisnih funkcija. Specifikacija tih funkcija je sljedeća:
void Upute(void);
/* Ispisuje igraču ploču, i upute za igru */
void OcistiPlocu(void);
/* Postavlja početno stanje,
* svi elementi matrice kvadrat imaju vrijednost ' '
*/
void PostaviPrvogIgraca(void);
/* Na temelju interakcije s korisnikom programa odlučuje da li
* prvi potez vuče računalo ili čovjek.
* Ako prvi potez vuče: racunalo = 'o'; covjek = 'X';
* inače: racunalo = 'X'; covjek = 'o';
*/
void IgrajIgru(void);
/* Ovom se funkcijom kontrolira tijek igre, interakcija s
* korisnikom, odlučuje o potezima koje inteligentno izvršava
* računalo i izvještava se o ispunjenosti igrače ploče. Funkcija
* završava kada se ispune uvjeti za pobjedu prvog ili drugog
* igrača ili ako su označeni svi kvadratići.
*/
int PonoviIgru(void);
/* Ovom funkcijom se od korisnika traži da potvrdi da li želi
* ponoviti igru. Ako korisnik želi ponoviti igru tada funkcija
* vraća 1, inače vraća vrijednost 0.
*/
Uz pretpostavku da će se kasnije uspješno implementirati ove funkcije, glavni program se može
napisati u obliku:
/* Program TicTacToe.c */
#include <stdio.h>
void Upute(void);
void OcistiPlocu(void);
void PostaviPrvogIgraca(void);
void IgrajIgru(void);
int PonoviIgru(void);
char kvadrat[3][3];
char racunalo, covjek;
121](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-121-320.jpg)
![int main(void)
{
Upute(); /* korak 1*/
do
{
OcistiPlocu(); /* korak 2*/
PostaviPrvogIgraca(); /* korak 3.*/
IgrajIgru(); /* korak 4.*/
}while(PonoviIgru()); /* korak 5.*/
return 0;
}
Što je do sada napravljeno?
Problem je rastavljen (dekomponiran) na pet manjih, međusobno neovisnih problema. Neki od
ovih problema se mogu odmah riješiti, primjerice funkcije Upute() i OcistiPlocu() se
mogu implementirati na sljedeći način:
void Upute()
{
printf("nIgra - tic tac toe - krizici i tockicenn");
printf("t | 1 | 2 | 3 | n");
printf("t |---|---|---| n");
printf("t | 4 | 5 | 6 | n");
printf("t |---|---|---| n");
printf("t | 7 | 8 | 9 | nn");
printf("Cilj igre je ispuniti tri kvadratica u redu: n");
printf("horizontalno, vertikalno ili dijagonalno. n"
printf("Igra se protiv racunala.n");
printf("Prvi igrac je oznacen krizicem X, a drugi tockicom o.nn");
}
void OcistiPlocu(void)
{
int redak, stupac;
for (redak = 0; redak < 3; redak++)
for (stupac = 0; stupac < 3; stupac++)
kvadrat[redak][stupac] = ' ';
}
Za ostale funkcije potrebna je daljnja dorada problema. Posebno opsežan problem je definiranje
funkcije IgrajIgru() u kojoj se obavlja više operacija. Prije definiranja te funkcije izvršit će
se definiranje funkcija PostaviPrvogIgraca() i PonoviIgru() jer je njihova
implementacija jednostavna i može se odrediti neposredno iz zadane specifikacije.
Dorada funkcije PostaviPrvogIgraca():
1. Izvijesti korisnika da on bira tko će povući prvi potez. Ako želi biti prvi na potezu neka
pritisne tipku 'D', inače neka pritisne tipku 'N'.
2. Motri korisnikov odziv, sve dok se ne pritisne jedna od ove dvije tipke.
3. Ako je pritisnuta tipka 'D', tada: racunalo = 'o'; covjek = 'X';
inače: racunalo = 'X'; covjek = 'o';.
void PostaviPrvogIgraca(void)
{
int key;
printf("Da li zelite zapoceti prvi? (d/n)n");
do {
key = toupper(getchar());
122](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-122-320.jpg)

![void IgrajIgru(void)
{
int potez = 1;
while (potez <= 9)
{
DobaviPotez(potez);
NacrtajPlocu();
if (PostajeDobitnik(racunalo)){
printf("nPobijedio sam te!!!nn");
break;
}
else if (PostajeDobitnik(covjek)) {
printf("nCestitam, pobijedio si!nn");
break;
}
potez++;
}
if (potez > 9)
printf("nOvaj put nema pobjednika.nn");
}
Realizacija funkcija DobaviPotez(), NacrtajPlocu() i PostajeDobitnik()
/* Funkcija: DobaviPotez(int potez)
* Izbor se dobije tako da se utvrdi
* da li je varijabla potez parna ili neparna.
* Ako je parna, igra 'X', inače igra 'o'
*/
void DobaviPotez(int potez)
{
if (potez % 2 == 1)
if (racunalo == 'X') PotezRacunala();
else PotezCovjeka();
else
if (racunalo == 'o') PotezRacunala();
else PotezCovjeka();
}
/* Funkcija: NacrtajPlocu()
* prikazuje igraču ploču na standardnom izlazu
*/
void NacrtajPlocu(void)
{
int redak, stupac;
printf("n");
for (redak = 0; redak < 3; redak++)
{
printf("t| %c | %c | %c |n",
kvadrat[redak][0], kvadrat[redak][1], kvadrat[redak][2]);
if (redak != 2)
printf("t|---|---|---|n");
}
printf("n");
return;
}
/* Funkcija: int PostajeDobitnik(char simbol)
* Provjera da li je simbol (X i o) pobjednik, ispitivanjem
124](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-124-320.jpg)
![* ispunjenosti redaka, stupaca ili dijagonala ploče
*/
int PostajeDobitnik(char simbol)
{
int redak, stupac;
for (redak = 0; redak < 3; redak++) /* ispitajmo 3 retka */
{
if ( (kvadrat[redak][0] == simbol)
&& (kvadrat[redak][1] == simbol)
&& (kvadrat[redak][2] == simbol))
return 1;
}
for (stupac = 0; stupac < 3; stupac++) /* ispitajmo 3 stupca */
{
if ( (kvadrat[0][stupac] == simbol)
&& (kvadrat[1][stupac] == simbol)
&& (kvadrat[2][stupac] == simbol))
return 1;
}
/* i konačno dvije dijagonalne kombinacije */
if ( (kvadrat[0][0] == simbol)
&& (kvadrat[1][1] == simbol)
&& (kvadrat[2][2] == simbol))
return 1;
if ( (kvadrat[0][2] == simbol)
&& (kvadrat[1][1] == simbol)
&& (kvadrat[2][0] == simbol))
return 1;
return 0;
}
/* Funkcija: PotezCovjeka(void) */
/* vrši dobavu poteza čovjeka */
void PotezCovjeka(void)
{
int pozicija;
do {
printf("Otipkaj poziciju znaka %c (1..9): ", covjek);
scanf("%d", &pozicija);
} while (!IspravnaPozicija(pozicija));
kvadrat[(pozicija - 1) / 3][ (pozicija - 1) % 3] = covjek;
}
/* Funkcija: IspravnaPozicija(int pozicija)
* vraća 1 ako pozicija prazna, inače vraća 0
*/
int IspravnaPozicija(int pozicija)
{
int redak, stupac;
redak = (pozicija - 1) / 3;
stupac = (pozicija - 1) % 3;
if ((pozicija >= 1) && (pozicija <= 9))
125](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-125-320.jpg)
![if (kvadrat[redak][stupac] == ' ')
return 1;
return 0;
}
/* Funkcija: PotezRacunala()
* inteligentno određuje potez racunala
* (algoritam je napisan u obliku komentara)
*/
void PotezRacunala(void)
{
int pozicija; /* pronađi kvadrat u kojem */
pozicija = DobitnaPozicija(racunalo); /* može pobijediti racunalo */
if (!pozicija) /* ako ga nema, pronađi */
pozicija = DobitnaPozicija(covjek); /* gdje čovjek pobijeđuje */
if (!pozicija) /* ako ga nema */
pozicija = PraznaSredina(); /* centar je najbolji potez */
if (!pozicija) /* ako ga nema */
pozicija = PrazanUgao(); /* najbolji je potez u kutovima */
if (!pozicija) /* ako ga nema */
pozicija = PrazanaStrana(); /* ostaje mjesto na stranicama */
printf("nJa sam izabrao kvadratic: %d!n", pozicija);
kvadrat[(pozicija - 1) / 3][ (pozicija - 1) % 3] = racunalo;
}
/*
* Funkcija: int DobitnaPozicija(char simbol),
* ako postoji dobitna kombinacija za simbol,
* vraća poziciju kvadratića, inaće vraća 0;
*/
int DobitnaPozicija(char simbol)
{
int pozicija, redak, stupac;
int rezultat = 0;
/* Analiziraj stanje u svih 9 kvadratića. Za svaki kvadratić:
* ako je prazan, ispuni ga danim simbolom, i provjeri da li je
* je to dobitni potez. Ako jest, zapamti ga u varijabli rezultat
* i ponovo poništi taj kvadratić.
* Nakon završetka petlje rezultat sadrži dobitni potez ili nulu ako
* nije pronađen dobitni potez.
* Funkcija vraća vrijednost varijable rezultat
*/
for (pozicija = 1; pozicija <= 9; pozicija++)
{
redak = (pozicija - 1) / 3;
stupac = (pozicija - 1) % 3;
if (kvadrat[redak][stupac] == ' ')
{
kvadrat[redak][stupac] = simbol;
if (is_wining(simbol))
rezultat = pozicija;
kvadrat[redak][stupac] = ' ';
}
}
return rezultat;
126](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-126-320.jpg)
![}
/* Funkcija: int PraznaSredina()
* vraća 5 ako je srednji kvadratić prazan, inaće vraća 0
*/
int PraznaSredina(void)
{
if (kvadrat[1][1] == ' ') return 5;
else return 0;
}
/* Funkcija: int PrazanUgao()
* vraća poziciju jednog od praznih kuteva,
* ako su svi kutevi zauzeti, vraća 0
*/
int PrazanUgao(void)
{
if (kvadrat[0][0] == ' ') return 1;
if (kvadrat[0][2] == ' ') return 3;
if (kvadrat[2][0] == ' ') return 7;
if (kvadrat[2][2] == ' ') return 9;
return 0;
}
/* Funkcija: int PrazanaStrana()
* vraća poziciju jedne od praznih stranica kvadrata,
* ako su sve pozicije zauzete vraća 0
*/
int PrazanaStrana(void)
{
if (kvadrat[0][1] == ' ') return 2;
if (kvadrat[1][0] == ' ') return 4;
if (kvadrat[1][2] == ' ') return 6;
if (kvadrat[2][1] == ' ') return 8;
return 0;
}
Slijed dekompozicije funkcija tipa "od vrha prema dolje" ilustriran je na slici 9.1.
127](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-127-320.jpg)

![10 Rad s pokazivačima
Naglasci:
• tip pokazivača
• operacije s pokazivačima
• ekvivalentnost reference niza i pokazivača
• prijenos varijable u funkciju
• void pokazivači
• pokazivači na funkcije
• polimorfne funkcije
Pokazivači su varijable koje sadrži adresu nekog memorijskog objekta: varijable ili
funkcije. Njihova primjena omogućuje napredne programske tehnike: dinamičko alociranje
memorije, apstraktni tip podataka i polimorfizam funkcija. Da bi se moglo shvatiti ove tehnike
programiranja, u ovom će poglavlju biti pokazano kako se vrše temeljne operacije s
pokazivačima, a u sljedećim će poglavljima biti pokazana njihova primjena u programiranju.
10.1 Tip pokazivača
Pokazivačkim varijablama se deklaracijom pridjeljuje tip. Deklariranje pokazivačke varijable se
vrši na način da se u deklaraciji ispred imena pokazivačke varijable upisuje zvjezdica *.
Primjerice,
int *p,*q; /* p i q su pokazivači na int */
označava da su deklarirane pokazivačke varijable p i q, kojima je namjena da sadrže adresu
objekata tipa int. Kaže se da su p i q "pokazivač na int".
Pokazivači, prije upotrebe, moraju biti inicijalizirani na neku realnu adresu. To se ostvaruje
tzv. adresnim operatorom &:
p = ∑ /* p iniciran na adresu varijable sum */
q = &arr[2]; /* q iniciran na adresu trećeg elementa niza arr*/
Adresa Vrijednost Identifikator
0x09AC -456 sum
0x09B0 ...... ......
...... ...... ......
0x0F10 ...... arr[0]
0x0F14 arr[1]
0x0F18 arr[2]
...... ......
0x1000 0x09AC p
0x1004 0x0F18 q
Slika 10.1 Adresa i vrijednost varijabli
129](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-129-320.jpg)
![10.2 Operacije s pokazivačima
Temeljne operacije s pokazivačima su:
1. Deklariranje pokazivača je postupak kojim se deklarira identifikator pokazivača, na
način da se između oznake tipa na koji pokazivač pokazuje i identifikatora pokazivača
upisuje se operator indirekcije *.
int x, *p; /* deklaracija varijable x i pokazivača p */
2. Inicijalizacija pokazivača je operacija kojom se pokazivaču pridjeljuje vrijednost koja
je jednak adresi objekta na koji on pokazuje. Za dobavu adrese objekta koristi se unarni
adresni operator '&' .
p = &x; /*p sadrži adresu od x */
3. Dereferenciranje pokazivača je operacija kojom se pomoću pokazivača pristupa
memorijskom objektu na kojega on pokazuje, odnosno, ako se u izrazima ispred
identifikatora pokazivača zapiše operator indirekcije *, dobiva se dereferencirani
pokazivač (*p). Njega se može koristiti kao varijablu, odnosno referencu memorijskog
objekta na koji on pokazuje.
y = *p; /* y dobiva vrijednost varijable koju p pokazuje*/
/* isti učinak kao y = x */
*p = y; /* y se pridjeljuje varijabli koju p pokazuje */
/* isti učinak kao x = y */
Djelovanje adresnog operatora je komplementarno djelovanju operatora indirekcije, i vrijedi da
naredba y = *(&x); ima isti učinak kao i naredba y = x;.
Unarni operatori * i & su po prioritetu iznad većine operatora (kada se koriste u izrazima).
y = *p + 1; ⇔ y = (*p) + 1;
Jedino postfiksni unarni operatori (-- ++, [], ()) imaju veći prioritet od * i & prefiks
operatora:
y = *p++; ⇔ y = *(p++);
Pokazivač kojem je vrijednost nula (NULL) naziva se nul pokazivač.
p = NULL; /* p pokazuja na ništa */
S dereferenciranim pokazivačem (*p) se može manipulirati kao sa varijablom pripadnog
tipa, primjerice,
int x, y, *px, *py;
px = &x; /* px sadrži adresu od x – ne utječe na x */
*px = 0; /* vrijednost x postaje 0 - ne utječe na px */
py = px; /* py također pokazuje na x - ne utječe na px ili x */
*py += 1; /* uvećava x za 1 - ne utječe na px ili py */
y = (*px)++; /* y = 1, a x =2 - ne utječe na px ili py */
130](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-130-320.jpg)

![Primjer: Definirana je funkciju swap(), pomoću koje se može izvršiti zamjena vrijednost
dvije varijable:
/* Datoteka: swap.c
* Zamjena vrijednosti dvije varijable pomoću swap funkcije */
*/
#include <stdio.h>
void swap( int *x, int *y)
{
int t;
t = *x;
*x = *y;
*y = t;
}
int main()
{
int a = 1, b = 2;
printf("a=%d b=%dn", a, b);
swap(&a , &b);
printf("Nakon poziva swap(&a, &b)n");
printf("a=%d b=%dn", a, b);
}
Ispis je:
a=1 b=2
Nakon poziva swap(&a, &b)
a=2 b=1
10.4 Pokazivači i nizovi
Potrebno je najprije navesti nekoliko pravila koje vrijede za reference niza i pokazivače
koji pokazuju na nizove. Analizirat ćemo niz a i pokazivač p:
int a[10];
int *p;
Pravila su:
1. Ime niza, iza kojeg slijedi oznaka indeksa, predstavlja element niza s kojim se manipulira na
isti način kao i sa prostim varijablama.
2. Ime niza, zapisano bez oznake indeksa je "pokazivačka konstanta - adresa" koja pokazuje na
prvi element niza. Ona se može pridijeliti pokazivačkoj varijabli. Naredbom
p = a;
za vrijednost pokazivača p postavlja se adresa a[0]. Ovo je ekvivalentno naredbi:
132](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-132-320.jpg)
![p = &a[0];
3. Pravilo pokazivačke aritmetike:
Ako p pokazuje na a[0], tada (p + i) pokazuje na a[i].
Ako pi pokazuje na a[i], tada pi + k pokazuje na a[i+k], odnosno, ako je
pi = &a[i];
tada vrijedi odnos;
*(pi+k) ⇔ *(p+i+k) ⇔ a[i+ k]
Gornja pravila određuju da se aritmetičke operacije s pokazivačima ne izvode na isti način
kao što se izvode aritmetičke operacije s cijelim brojevima.
Za prosti cijeli broj x vrijedi:
vrijednost(x ± n) = vrijednost(x) ± n
dok za pokazivač p vrijedi
vrijednost(p ± n) = vrijednost(p) ± n*sizeof(*p)
4. Ekvivalentnost indeksne i pokazivačke notacije niza.
Ako je deklariran niz array[N], tada izraz *array označava prvi element, *(array +
1) predstavlja drugi element, itd. Poopći li se ovo pravilo na cijeli niz, vrijede sljedeći odnosi:
*(array) ⇔ array[0]
*(array + 1) ⇔ array[1]
*(array + 2) ⇔ array[2]
...
*(array + n) ⇔ array[n]
što odgovara činjenici da ime niza predstavlja pokazivačku konstantu.
S pokazivačima se također može koristiti indeksna notacija. Tako, ako je inicijaliziran
pokazivač p:
p = array;
tada vrijedi:
p[0] ⇔ *p ⇔ array[0]
p[1] ⇔ *(p + 1) ⇔ array[1]
p[2] ⇔ *(p + 2) ⇔ array[2]
...
p[n] ⇔ *(p + n) ⇔ array[n]
Jedina razlika u korištenju reference niza i pokazivača na taj niz je u tome da se
memorijskim referencama ne može mijenjati vrijednost adrese koju oni
označavaju.
a++; je nedozvoljen izraz, jer se ne može mijenjati konstanta
133](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-133-320.jpg)
![p++; je dozvoljen izraz, jer je pokazivač p varijabla
Pošto se pokazivaču može mijenjati vrijednost, obično se kaže da se pomoću pokazivača može
"šetati po nizu".
Primjer: U obje sljedeće petlje ispisuje se vrijednost 10 elemenata niza a.
int *p = a;
for (i = 0; i < 10; i++, p++) for (i = 0; i < 10; i++)
printf("%dn", *p); printf("%dn", a[i]);
U prvoj petlji se koristi pokazivač p za pristup elementima niza a[]. Početno on pokazuje na
prvi element niza a[]. U petlji se zatim ispisuje vrijednost tog elementa (dereferencirani
pokazivač *p), i inkrementira vrijednost pokazivača, tako da se u narednom prolazu petlje s
njime referira sljedeći element.
Kompilator ne prevodi ove petlje na isti način, iako je učinak u oba slučaja isti: bit će
ispisana vrijednost 10 elemenata niza a[]. Ako je učinak isti, možemo se dalje upitati koja će se
od ovih petlji brže izvršavati. To ovisi o kvaliteti kompilatora i o vrsti procesora. Kod starijih
procesora brže se izvršava verzija s pokazivačem, jer se u njoj u jednom prolazu petlje vrše dva
zbrajanja, dok se u drugom slučaju mora (skriveno) izvršiti i jedno množenje. Ono je potrebno
da bi se odredila adresa elementa a[i], jer je
adresa(a[i])= adresa(a[0]) + i*sizeof(int).
Kod novijih se procesora operacija indeksiranja izvršava veoma brzo, pa se u tom slučaju
preporučuje korištenje verzije s indeksnim operatorom.
10.5 Pokazivači i argumenti funkcije tipa niza
Pri pozivu funkcije, stvarni se argument kopira u formalni argument (parametar) funkcije.
U slučaju da je argument funkcije ime niza kopira se adresa prvog elementa, dakle stvarni
argument koji se prenosi u funkciju je vrijednost pokazivača na prvi element niza. Stoga se
prijenos niza u funkciju može deklarirati i pomoću pokazivača.
Primjer: Sljedeće tri funkcije imaju isti učinak i mogu se pozvati s istim argumentima:
void print(int x[], void print(int *x, void print(int *x,
int N ) int N) int N)
{ { {
int i; while (N--) { int i;
for (i = 0; i < N; i++) for (i=0; i<N;i++)
printf("%dn", x[i]); printf("%dn", *x); printf("%dn", x[i]);
} x++; }
}
}
/* poziv funkcije print */
int niz[10], size=10;
. . . . .
print(niz, size);
134](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-134-320.jpg)
![const osigurači
U prethodnom primjeru u funkciji print() se koriste vrijednosti elemenata niza x, a ne
mijenja se njihova vrijednost. U takovim slučajevima je preporučljivo da se parametri funkcije
deklariraju s prefiksom const.
void print(const int x[], int N );
ili void print(const int *x, int N );
Ovakva deklaracija je poruka kompilatoru da dojavi grešku ako u funkciji postoji naredba
kojom se mijenja sadržaja elemenata niza, a programeru služi kao dodatno osiguranje da će
izvršiti implementaciju funkcije koja neće mijenjati elemente niza.
Pomoću pokazivača se u funkcije mogu prenositi i proste varijable i nizovi.
Primjer: Napisat ćemo funkciju getMinMax() kojom se određuje maksimalna i minimalna
vrijednost niza. Testirat ćemo je programom u kojem korisnik unosi 5 brojeva, a program
ispisuje maksimalnu i minimalnu vrijednost.
/* Datoteka: minmax.c */
#include <stdio.h>
#define N 5 /* radit ćemo s nizom od N elemenata */
void getMinMax(double *niz, int nelem, double *pMin, double *pMax)
{
/* funkcija određuje minimalni i maksimalni element niza
* Parametri funkcije su:
* niz – niz realnih brojeva
* nelem – broj elemenata u nizu
* pMin – pokazivac na minimalnu vrijednost
* pMax - pokazivac na maksimalnu vrijednost
/*
int i= 0;
*pMin = *pMax = niz[0];
for(i=1; i<N; i++) {
if(niz[i] > *pMax ) *pMax = niz[i];
if(niz[i] < *pMin) *pMin = niz[i];
}
}
int main()
{
int i;
double min, max, data [N];
/* 1. izvjesti korisnika da otkuca 5 realnih brojeva */
printf("Otkucaj %d realnih brojeva:n", N);
for (i=0; i<N; i++)
scanf("%lg", &data[i]);
getMinMax(data, N, &min, &max);
/* ispisi minimalnu i maksimalnu vroijednost */
printf ("min = %lf max = %lfn", min, max);
return 0;
}
135](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-135-320.jpg)



![double (*pF[4])(double) = {sin, cos, tan, exp};
deklariran je niz od 4 elementa koji sadrže pokazivač na funkciju kojoj je parametar tipa
double i koja vraća vrijednost tipa double. Također je izvršena i inicijalizacija elemenata niza
na adresu standardnih matematičkih funkcija.
Sada je naredba x = (*pF[1])(3.14) ekvivalentna naredbi x= cos(3.14).
Primjer: U programu niz-pfun.c koristi se niz pokazivača na funkciju. U nizu se bilježe
adrese funkcija sin(), cos() i korisnički definirane funkcije Kvadrat(). Zatim se od
korisnika traži da unese broj i da odabere funkciju. Na kraju se ispisuje rezultat primjene
funkcije na uneseni broj.
/* Datoteka: niz-pfun.c
* korištenje niza pokazivača na funkciju
*/
#include <stdio.h>
#include <math.h>
double Kvadrat (double x) {return x*x;}
int main()
{
double val=1;
int izbor;
double (*pF[3])(double)= {Kvadrat, sin, cos};
printf("Upisi broj:");
scanf("%lf", &val);
fflush(stdin);
printf( "n(1)Kvadrat n(2)Sinus n(3)Kosinus n");
printf( "nOdaberi 1, 2 li 3n");
scanf("%d" ,&izbor);
if (izbor >=1 && izbor <=3)
printf( "nRezultat je %lfn", (*pF[izbor-1])(val));
return 0;
}
10.8 Kompleksnost deklaracija
Očito je da se u C jeziku koriste vrlo kompleksne deklaracije. One na prvi pogled ne otkrivaju o
kakovim se tipovima radi. Sljedeća tablica pokazuje deklaracije koje se često koriste.
U deklaraciji: x je ime koje predstavlja ...
T x; objekt tipa T
T x[]; (otvoreni) niz objekata tipa T
T x[n]; niz od n objekata tipa T
T *x; pokazivač na objekt tipa T
T **x; pokazivač na pokazivač tipa T
T *x[]; niz pokazivača na objekt T
T *(x[]); niz pokazivača na objekt T
139](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-139-320.jpg)
![T (*x)[]; pokazivač na niz objekata tipa T
T x(); funkcija koja vraća objekt tipa T
T *x() funkcija koja vraća pokazivač na objekt tipa T
T (*x()); funkcija koja vraća pokazivač na objekt tipa T
T (*x)(); pokazivač na funkciju koja vraća objekt tipa T
T (*x[n])(); niz od n pokazivača na funkciju koja vraća objekt tipa T
Dalje će biti pokazano:
1. Kako sistematski pročitati ove deklaracije.
2. Kako se uvođenjem sinonima tipova (pomoću typedef) može znatno smanjiti
kompleksnost deklaracija.
Deklaracija nekog identifikatora se čita ovim redom:
Identifikator je (... desna strana deklaracije) (.. lijeva strana deklaracije)
S desne strane identifikatora mogu biti uglate ili oble zagrade.
Ako su uglate zagrade čitamo : identifikator je niz ,
Ako su oble zagrade čitamo identifikator je funkcija.
Ukoliko ima više operatora s desne strane nastavlja se čitanje po istom pravilu.
Zatim se analizira zapis s lijeve strane identifikatora ( tu može biti operator indirekcije i
oznaka tipa).
Ako postoji operator indirekcije, čitamo: identifikator je (... desna strana) pokazivač na
tip. Ako postoji dvostruki operator indirekcije, čitamo: identifikator je (... desna strana)
pokazivač na pokazivač tip
Ukoliko je dio deklaracije napisan u zagradama onda se najprije čita značaj zapisa u
zagradama.
Primjerice, u deklaraciji
T (*x[n])(double);
najprije se čita dio deklaracije (*x[n]) koji znači da je x niz pokazivača. Pošto je s desne strane
ovog izraza (double) znači da je x niz pokazivača na funkciju koja prima argument tipa
double i koja vraća tip T.
Znatno jednostavniji i razumljiviji način zapisa kompleksnih deklaracija postiže se korištenjem
sinonima za kompleksne tipove. Sinonimi tipova se definiraju pomoću typedef. Primjerice,
typedef deklaracijom
typedef double t_Fdd(double); /* tip funkcije ... */
uvodi se oznaka tipa t_fdd koja predstavlja funkciju koja vraća double i prima argument tipa
double.
Dalje se može definirati tip t_pFdd koji je pokazivač na funkciju koja vraća double i prima
argument tipa double, s deklaracijom:
typedef t_Fdd *t_pFdd; /* tip pokazivača na funkciju ...*/
140](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-140-320.jpg)
![što je ekvivalentno deklaraciji sinonima tipa:
typedef double (*t_pFdd)(double);
Pomoću tipa t_pFdd može se deklarirati niz pokazivača na funkciju iz prethodnog programa:
t_pFdd pF[3] = {Kvadrat, sin, cos};
Očito da je ovakovu deklaraciju znatno lakše razumjeti.
Primjer: Primjeni li se navedene typedef deklaracije u programu niz-pfun.c, dobije se
/* Datoteka: niz-pfun1.c */
#include <stdio.h>
#include <math.h>
typedef double t_Fdd(double); /* tip funkcije koja ... */
typedef t_pFdd *t_pFdd; /* tip pokazivača na funkciju ...*/
double Kvadrat (double x) {return x*x;}
void PrintVal(t_pFdd pFunc, double x)
{
printf( "nZa x: %lf dobije se %lfn", x, pFunc(x));
}
int main()
{
double val=1;
int izbor;
t_pFdd pF[3] = {Kvadrat, sin, cos};
printf("Upisi broj:");
scanf("%lf", &val);
fflush(stdin);
printf( "n(1)Kvadrat n(2)Sinus n(3)Kosinus n");
printf( "nOdaberi 1, 2 li 3n");
scanf("%d" ,&izbor);
if (izbor >=1 && izbor <=3)
printf( "nRezultat je %lfn", (*pF[izbor-1])(val));
return 0;
}
10.9 Polimorfne funkcije
Funkcije koje se mogu prilagoditi različitim tipovima argumenata nazivaju se polimorfne
funkcije. Polimorfne funkcije se u C jeziku realiziraju pomoću parametara koji imaju tip void
pokazivača i pokazivača na funkcije. Dvije takove funkcije implementirane su u standardnoj
biblioteci C jezika. To su qsort() i bsearch() funkcija, čija je deklaracija dana u
<stdlib.h>.
void qsort(void *a, /* pokazivač niza */
size_t n, /* broj elemenata */
size_t elsize, /* veličina elementa u bajtima */
141](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-141-320.jpg)
![int (*pCmpF)(void *, void *))
qsort() funkcija služi za sortiranje elemenata niza a, koji sadrži n elemenata veličine
elsize bajta. Elementi se sortiraju od manje prema većoj vrijednosti, odnosno prema kriteriju
usporedbe koji određuje funkcija (*pCmpF)().
Usporedna funkcija mora biti deklarirana u obliku
int ime_funkcije(const void *p1, const void *p2);
Argumenti ove funkcije su pokazivači na dva elementa niza. Funkcija mora vratiti vrijednost
nula ako su ta dva elementa jednaka, pozitivnu vrijednost ako je prvi element veći od drugoga, a
negativnu vrijednost ako je prvi element manju od drugoga.
Primjerice, za sortiranje niza cijelih brojeva usporedna funkcija ima oblik:
int CmpInt(const void *p1, const void *p2)
{
int i1 = *((int *)p1);
int i2 = *((int *)p2);
if( i1 == i2)
return 0;
else if( i1 > i2)
return 1;
else
return -1; /* i2 > i1 */
}
Najprije se s adresa p1 i p2 dobavlja cjelobrojne vrijednosti i1 i i2. Dobava vrijednosti se
vrši tako da se najprije izvrši pretvorba void pokazivača u int*, a zatim se primijeni
indirekcija pokazivača. Nakon toga se vrši usporedba vrijednosti i vraća dogovorena vrijednost.
Testiranje primjene funkcije qsort() je u programu sorti.c. U programu se vrši
sortiranje niza cijelih brojeva.
/* Datoteka: sorti.c */
/* koristenje polimorfne qsort funkcije */
#include <stdio.h>
#include <stdlib.h>
int CmpInt(const void *p1, const void *p2)
{ ...... prethodna definicija ... }
int main()
{
int i, A[] = {3,1,13,2,17};
int numel=sizeof(A)/sizeof(A[0]);
int elsize = sizeof(A[0]);
for(i=0; i <numel; i++)
printf(" %d", A[i]);
printf("n Nakon sortiranjan");
qsort(A, numel, elsize, CmpInt);
142](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-142-320.jpg)
![for(i=0; i <numel; i++)
printf(" %d", A[i]);
printf("n");
return 0;
}
Nakon izvršenja dobije se ispis:
3 1 13 2 17
Nakon sortiranja
1 2 3 13 17
Zadatak: Napišite program sortf.c u kojem se vrši sortiranje niza realnih brojeva. Koristite
qsort() funkciju. Definirajte prikladnu usporednu funkciju int FloatCmp(..).
Funkcija za polimorfno traženje elementa niza
Slijedi opis polimorfne funkcije search() kojom se određuje da li u nekom nizu postoji
element zadane vrijednosti. Funkcija vraća pokazivač na traženi element, ako postoji , ili NULL
ako u tom nizu ne postoji zadana vrijednost. Koristi se deklaracija funkcije slična funkciji
qsort(), jedino se još dodaje argument tipa void pokazivača na varijablu koja sadrži vrijednost
koju se traži u nizu A.
void * search(const void *x, /* pokazivač na zadanu vrijednost */
const void *A, /* pokazivač niza A*/
size_t n, /* broj elementa niza */
size_t elsize, /* veličina elementa u bajtima */
int (*pCmpF)( const void *, const void *)) /*funkcija */
{
int indx;
char *adr;
for(indx = 0; indx < n; indx++)
{
adr= (char*)A +indx*elsize; /* adresa elementa niza */
if( (*pCmpF)((void *)adr, x) == 0)
break;
}
if(indx == n) /* tada ni jedan element nema vrijednost x*/
return NULL;
else
return (void *) adr; /*vrati adresu elementa */
}
Testiranje primjene funkcije search() vrši se programom searchi.c:
/* Datoteka: searchi.c*/
#include <stdio.h>
#include <stdlib.h>
void *search(const void *x, const void *A, size_t n,
size_t elsize,
int (*pCmpF)( const void *, const void *))
{
143](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-143-320.jpg)
![....... prema prethodnoj definiciji
}
int CmpInt(const void *p1, const void *p2)
{
....... prema prethodnoj definiciji
}
int main()
{
int i, indx, x = 2; /* x- tražena vrijednost */
int A[] = {3,1,13,2,17, 7, 0, 11}; /* u nizu A*/
int numel=sizeof(A)/sizeof(A[0]);
int elsize = sizeof(A[0]);
int *pEl;
for(i=0; i <numel; i++)
printf(" %d", A[i]);
pEl=(int *) search(&x, A, numel, elsize, CmpInt);
printf("n Element vrijednosti %d, na adresi %Fpn", *pEl, pEl);
printf("n");
return 0;
}
Nakon izvršenja dobije se ispis:
3 1 13 2 17 7 0 11
Element vrijednosti 2, na adresi 0022FF4C
U standardnoj biblioteci je implementirana funkcija bsearch() koja ima istu deklaraciju
kao funkcija search(). Razlika ove dvije funkcije je u tome što je bsearch() funkcija
specijalizirana i optimirana za slučaj da se traženje elementa niza provodi na prethodno
sortiranom nizu. Kasnije ćemo pokazati kako su realizirane funkcije bsearch() i qsort().
10.10 Zaključak
Pokazivači zauzimaju središnje mjesto u oblikovanju C programa. Pokazivač je varijabla
koja sadrži adresu. Ako je to adresa varijable, kaže se da pokazivač "pokazuje" na tu varijablu.
U radu s pokazivačima koriste se dva specifična operatora: adresni operator (&) i operator
indirekcije(*). Adresni operator napisan ispred imena varijable vraća u izraz adresu varijable, a
operator indirekcije *, postavljen ispred imena pokazivača, referira sadržaj varijable na koju
pokazivač pokazuje.
Pokazivači i nizovi su u specijalnom odnosu. Ime niza, napisano bez uglatih zagrada
predstavlja pokazivačku konstanu koja pokazuje na prvi element niza.
Indeksna notacija ima ekvivalentni oblik pokazivačke notacije. Uglate zagrade imaju
karakter indeksnog operatora, jer kada se koriste iza imena pokazivača, uzrokuju da se tim
pokazivačem može operirati kao s nizom.
Nizovi se prenose u funkcije na način da se u funkciju prenosi pokazivač na prvi element
niza, odnosno adresa prvog elementa niza. Pošto funkcija zna adresu niza, u njoj se mogu
144](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-144-320.jpg)

![11 Nizovi znakova - string
Naglasci:
• ASCIIZ stringovi
• standardne funkcije za rad sa stringovima
• ulazno izlazne operacije sa stringovima
• konverzije stringa
• nizovi stringova
• argumenti komandne linije operativnog sustava
Bit će pokazano kako se formiraju i obrađuju nizovi znakova. Od posebnog interesa su
nizovi znakova koji imaju karakteristike stringa.
11.1 Definicija stringa
String je naziv za memorijski objekt koji sadrži niz znakova, a posljednji znak u nizu mora
biti nulti znak ('0'). Deklarira se kao niz znakova (pr. char str[10]) , ili kao pokazivač
na znak (char *str), ali pod uvjetom da se pri inicijalizaciji niza i kasnije u radu s nizom
uvijek vodi računa o tome da posljednji element niza mora biti jednak nuli. Zbog ove se
karakteristike stringovi u C jeziku nazivaju ASCIIZ stringovi. Sastoje od niza ASCII znakova i
nule (eng. Z - zero).
Duljina stringa je cjelobrojna vrijednost koja je jednaka broju znakova u stringu (bez nultog
znaka). Indeks "nultog" znaka jednak je broju znakova u stringu, odnosno duljini stringa.
Primjerice, string koji sadrži tekst: Hello, World!, u memoriji zauzima 14 bajta. Njegova duljina
je 13, jer je indeks nultog znaka jednak 13.
0 1 2 3 4 5 6 7 8 9 10 11 12 13
H e l l o , W o r l d ! 0
Pogledajmo primjer u kojem se string tretira kao niz znakova.
/* Prvi C program – drugi put. */
#include <stdio.h>
#include <string.h>
int main()
{
char hello[14] = { 'H', 'e', 'l', 'l', 'o', ',', ' ',
'W', 'o', 'r', 'l', 'd', '!', '0' };
printf("%sn", hello);
printf("Duljina stringa je %d.n", strlen(hello));
return 0;
}
146](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-146-320.jpg)
![Nakon izvršenja programa, dobije se poruka:
Hello, World!
Duljina stringa je 13.
Ovaj program vrši istu funkciju kao i prvi C-program iz ove knjige, tiska poruku: Hello,
World!. U programu je prvo definirana i inicijalizirana varijabla hello. Ona je tipa znakovnog
niza od 14 elemenata. Inicijalizacijom se u prvih 13 elemenata upisuju znakovi (Hello World!),
a posljednji element se inicira na nultu vrijednost. Ispis ove varijable se vrši pomoću printf()
funkcije sa specifikatorom formata ispisa %s.
Duljina stringa je određena korištenjem standardne funkcije
size_t strlen(char *s);
Parametar funkcije je pokazivač na char, odnosno, pri pozivu funkcije argument je adresa
početnog elementa stringa. Funkcija vraća vrijednost duljine stringa (size_t je sinonim za
unsigned).
Funkcija strlen() se može implementirati na sljedeći način:
unsigned strlen(const char *s)
{
unsigned i=0;
while (s[i] != '0') /* prekini petlju za s[i]==0, inače */
i++; /* inkrementiraj brojač znakova */
return i; /* i sadrži duljinu stringa */
}
ili pomoću pokazivačke aritmetike:
unsigned strlen(const char *s)
{
unsigned i = 0;
while (*s++ != '0') /* prekini petlju za *s==0, inače */
i++; /* inkrementiraj brojač i pokazivač*/
return i; /* i sadrži duljinu stringa */
}
String se može inicijalizirati i pomoću literalne konstante:
char hello[] = "Hello, World!"; /* kompilator rezervira mjesto u
memoriji */
Elementi stringa se mogu mijenjati naredbom pridjele vrijednosti, primjerice naredbe:
hello[0] = 'h';
hello[6] = 'w';
mijenjaju sadržaj stringa u "hello world";
Ako se procjenjuje da će trebati više mjesta za string, nego se to navodi inicijalnim
literalnim stringom, tada treba eksplicitno navesti dimenziju stringa. Primjerice, deklaracijom
char hello[50] = "Hello, World!";
147](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-147-320.jpg)
![kompilator rezervira 50 mjesta u memoriji te inicira prvih 14 elemenata na "Hello, World!",
zaključno s nultim znakom.
String je i svaki pokazivač koji se inicijalizira na adresu memorijskog objekta koji ima
karakteristike stringa. Stoga, i sljedeći iskaz predstavlja deklaraciju stringa:
char *digits ="0123456789ABCDEF";
/* kompilator inicijalizira pokazivač */
/* na adresu od "0123456789ABCDEF"; */
Ovakva inicijalizacija je moguća jer kompilator interno literalni string tretira kao referencu,
pa se njegova adresa pridjeljuje pokazivaču digits. Dozvoljeno je čak literalnu string
konstantu koristiti kao referencu niza, primjerice
printf("%c", "0123456789ABCDEF"[n]);
ispisuje n-ti znak stringa "0123456789ABCDEF".
11.2 Standardne funkcije za rad sa stringovima
U standardnoj biblioteci postoji niz funkcija za manipuliranje sa stringovima. One su
deklarirane u datoteci "string.h". Funkcija im je:
size_t strlen(const char *s)
Vraća duljinu stringa s.
char *strcpy(char *s, const char *t)
Kopira string t u string s, uključujući '0'; vraća s.
char *strncpy(char *s, const char *t, size_t n)
Kopira najviše n znakova stringa t u s; vraća s. Dopunja string s sa '0' znakovima ako t
ima manje od n znakova.
char *strcat(char *s, const char *t)
Dodaje string t na kraj stringa s; vraća s.
char *strncat(char *s, const char *t, size_t n)
Dodaje najviše n znakova stringa t na string s, i znak '0'; vraća s.
int strcmp(const char *s, const char *t)
Uspoređuje string s sa stringom t, vraća <0 ako je s<t, 0 ako je s==t, ili >0 ako je s>t.
Usporedba je leksikografska, prema ASCII "abecedi".
int strncmp(const char *s, const char *t, size_t n)
Uspoređuje najviše n znakova stringa s sa stringom t; vraća <0 ako je s<t, 0 ako je s==t, ili
>0 ako je s>t.
char *strchr(const char *s, int c)
Vraća pokazivač na prvu pojavnost znaka c u stringu s, ili NULL znak ako c nije sadržan u
stringu s.
148](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-148-320.jpg)

![char *strcpy( char *dst, const char *src)
{
int i;
for (i = 0; src[i] != '0'; i++)
dst[i] = src[i];
dst[i] = '0';
return dst;
}
2. Verzija s pokazivačkom aritmetikom
char *strcpy(char *dest, const char *src)
{
char *d = dest;
while(*d = *src) /* true dok src ne bude '0'*/
{
d++;
src++;
}
return dest;
}
Funkcija strcmp()služi usporedbi dva stringa s1 i s2. Deklarirana je s:
int strcmp(const char *s1, const char *s2)
Funkcija vraća vrijednost 0 ako je sadržaj oba stringa isti, negativnu vrijednost ako je s1
leksički manji od s2, ili pozitivnu vrijednost ako je s1 leksički veći od s2. Leksička usporedba
se izvršava znak po znak, prema kodnoj vrijednosti ASCII standarda.
/*1. verzija*/
int strcmp( char *s1, char *s2)
{
int i = 0;
while(s1[i] == s2[i] && s1[i] != '0')
i++;
if (s1[i] < s2[i])
return -1;
else if (s1[i] > s2[i])
return +1;
else
return 0;
}
Najprije se u glavi petlje uspoređuje da li su znakovi s istim indeksom isti i da li je dostignut
kraj niza (znak '0'). Kad petlja završi, ako su oba znaka jednaka, to znači da su i svi prethodni
znakovi jednaki. U tom slučaju funkcija vraća vrijednost 0. U suprotnom funkcija vraća 1 ili –1
ovisno o numeričkom kodu znakova koji se razlikuju.
/*2. verzija s inkrementiranjem pokazivača*/
int strcmp(char *s1, char *s2)
{
while(*s1 == *s2)
{
if(*s1 == '0')
return 0;
s1++;
150](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-150-320.jpg)
![s2++;
}
return *s1 - *s2;
}
Verzije u kojima se koristi inkrementiranje pokazivačka često su kod starije
generacije procesora rezultirale bržim izvršenjem programa. Kod novije generacije
procesora to nije slučaj, pa se preporučuje korištenje indeksne notacije.
11.3 Ulazno-izlazne operacije sa stringovima
Najjednostavniji način dobave i ispisa stringa je da se koriste printf() i scanf()
funkcije s oznakom formata %s. Primjerice, s
char line[100];
scanf("%s",str);
printf("%s", str);
najprije se vrši unos stringa (korisnik otkuca niz znakova i <enter>). Zatim se vrši ispis tog
stringa pomoću printf() funkcije.
Funkcija scanf() nije pogodna za unos stringova u kojima ima bijelih znakova, jer i oni znače
kraj unosa, stoga se za unos i ispis stringa češće koriste funkcije:
char *gets(char *str);
int puts(char *str);
Funkcija gets() dobavlja liniju teksta sa standardnog ulaza (unos se prekida kada je na ulazu
'n') i sprema je u string str, kojeg zaključuje s nul znakom. Podrazumijeva se da je prethodno
rezervirano dovoljno memorije za smještaj stringa str. Funkcija vraća pokazivač na taj string
ili NULL ako nastupi greška ili EOF.
Funkcija puts() ispisuje string str na standardni izlaz. Vraća pozitivnu vrijednost ili -1 (EOF)
ako nastupi greška. Jedina razlika između funkcije printf("%s", str) i puts(str) je u
tome da funkcija puts(str) uvijek na kraju ispisa dodaje i znak nove linije.
Primjer: U programu str-io.c pokazana je upotreba raznih funkcija za rad sa stringovima.
Program dobavlja liniju po liniju teksta sve dok se ne otkuca: "kraj". Nakon toga se ispisuje
ukupno uneseni tekst.
/* str-io.c */
#include <stdio.h>
#include <ctype.h>
#include <string.h>
#define MAXCH 2000
int main( void)
{
char str[100]; /* string u kojeg se unosi jedna linija teksta */
char text[MAXCH]; /* string u kojeg se zapisuje ukupno uneseni tekst*/
/* iniciraj string text sa sljedecim tekstom */
151](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-151-320.jpg)

![int getstring(char *str, int maxchar);
Parametri ove funkcije su string str i cijeli broj maxchar, kojim se zadaje maksimalno
dozvoljeni broj znakova koji će biti spremljen u string. Funkcija vraća broj znakova ili 0 ako je
samo pritisnut znak nove linije ili EOF ako je na početku linije otipkano Ctrl-Z.
Funkcija getstring() se može implementirati na sljedeći način:
#include <stdio.h>
int getstring(char *str, int maxchar)
{
int ch, nch = 0; /* početno je broj znakova = 0 */
--maxchar; /* osiguraj mjesto za '0' */
while((ch = getchar()) != EOF) /* dobavljaj znak */
{
if(ch == 'n') /* prekini unos na kraju linije */
break;
/* prihvati unos samo ako je broj znakova < maxchar */
if(nch < maxchar)
str[nchar++] = ch;
}
if(ch == EOF && nch == 0)
return EOF;
str[nch] = '0'; /* zaključi string s nul znakom */
return nch;
}
Testiranje ove funkcije provodi se programom getstr.c. U njemu korisnik unosi više linija
teksta, a unos završava kada se otkuca Ctrl-Z.
#include <stdio.h>
int getstring(char *, int);
main()
{
char str[256];
while(getstring(str, 256) != EOF)
printf("Otipkali ste "%s"n", str);
return 0;
}
11.5 Pretvorba stringa u numeričku vrijednost
Funkciju getstring()se može iskoristiti i za unos numeričkih vrijednosti, jer u
standardnoj biblioteci postoje funkcije
153](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-153-320.jpg)
![int atoi(char *str);
double atof(char *str);
koje vrše pretvorbu znakovnog zapisa u numeričku vrijednost. Ove funkcije su deklarirane u
<stdlib.h>. Funkcija atoi() pretvara string u vrijednost tipa int a funkcija atof()
pretvara string u vrijednost tipa double. Podrazumijeva se da string sadrži niz znakova koji se
koriste za zapis numeričkih literala. U slučaju greške ove funkcije vraćaju nulu. Greška se
uvijek javlja ako prvi znak nije znamenka ili znakovi + i -.
Primjer: U programu str-cnv.c prikazano je kako se može vršiti unos numeričkih vrijednosti
pomoću funkcija getstring(), atoi() i atof():
/* str-cnv.c */
#include <stdio.h>
#include <stdlib.h>
int getstring(char *, int);
#define NCHARS 30
int main()
{
int i;
double d;
char str [NCHARS];
puts("Otipkajte cijeli broj");
getstring(str, NCHARS);
i = atoi(str);
printf("Otipkali ste %dn", i);
puts("Otipkajte realni broj");
getstring(str, NCHARS);
d = atof(str);
printf("Otipkali ste %lgn", d);
return 0;
}
Drugi način da se iz stringa dobije numerička vrijednost je da se koristi funkcija sscanf().
int sscanf (char *str, char *format, ... );
Ova funkcija ima isto djelovanje kao funkcija scanf(). Razlika je u tome da sscanf() prima
znakove iz stringa str, dok funkcija scanf() prima znakove sa standardnog ulaza.
Primjer: pretvorba stringa, koji sadrži znakovni zapis cijelog broja, u numeričku vrijednost
cjelobrojne varijable vrši se iskazom
sscanf( str, "%d", &i);
Ponekad će biti potrebno izvršiti pretvorbu numeričke vrijednosti u string. U tom slučaju se
može koristiti standardna funkcija:
int sprintf(char *str, char *format, ... );
154](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-154-320.jpg)
![koja ima isto djelovanje kao printf() funkcija, ali se ispis vrši u string, a ne na standardni
izlaz.
11.6 Nizovi stringova
Nizovi stringova se jednostavno deklariraju i inicijaliziraju kao nizovi pokazivača na
char. Primjerice, za rad s igračkim kartama može se koristiti dva niza stringova: jedan za boju,
a drugi za lik karata. Deklariraju se na sljedeći način:
char *boja[] = {"Srce", "Tref", "Karo", "Pik "};
char *lik[] = {"As", "2", "3", "4", "5",
"6", "7", "8", "9", "10",
"Jack", "Dama", "Kralj" };
Pojedinom stringu se pristupa pomoću indeksa, primjerice boja[2] označava string "Karo".
Pri deklaraciji se koristi pravilo da operator indirekcije ima niži prioritet od uglatih zagrada, tj.
da je deklaracija char *boja[] ekvivalentna deklaraciji: char *( boja []), pa se
iščitava: boja je niz pokazivača na char. Isto vrijedi i za upotrebu varijable lik. Primjerice,
*lik[i] se odnosi na prvi znak i-tog stringa (tj. lik[i][0]).
Primjer: Dijeljenje karata
Program karte.c služit će da se po slučajnom uzorku izmiješaju igrače karte. Za miješanje
karate koristi se proizvoljna metoda:
Postoje 52 karte. Njih se registrira u nizu cijelih brojeva int karte[52]. Svaka karta[i]
sadrži vrijednost iz intervala 0..51 koja označava kombinaciju boje i lika karte, prema pravilu :
oznaka boje: boja[karte[i] / 13]; /* string boja[0 do 3] */
oznaka lika: lik [karte[i] % 13]; /* string lik[0 do 12] */
jer ima 13 likova i 4 boje. To znači da ako se početni raspored inicijalizira s
for (i = 0; i < BROJKARATA; i++)
karte[i] = i;
karte će biti složene po bojama, od asa prema kralju (prva će biti as-srce a posljednja kralj-pik).
Za miješanje karata koristit će se standardna funkcija
int rand();
koja je deklarirana u <stdlib.h>. Ova funkcija pri svakom pozivu vraća cijeli broj iz
intervala 0 do RAND_MAX (obično je to vrijednost 32767) koji se generira po slučajnom uzorku.
Kasnije će biti pokazano kako je implementirana ova funkcija.
Miješanje karata se provodi na način da se položaj svake karte zamijeni s položajem koji se
dobije po slučajnom zakonu:
for (i = 0; i < BROJKARATA; i++)
{
int k = rand() % BROJKARATA;
swap (&karte[i], &karte[k]);
}
/* Datoteka: karte.c - dijeljenje karata*/
155](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-155-320.jpg)
![#include <stdio.h>
#include <stdlib.h>
char *boja[] = {"Srce", "Tref", "Karo", "Pik "};
char *lik[] = {"As", "2", "3", "4", "5", "6", "7", "8",
"9", "10", "Jack", "Dama", "Kralj" };
#define BROJKARATA 52
void swap(int *x, int *y)
{
int t = *x;
*x = *y;
*y = t;
}
int main( void)
{
int i, karte[BROJKARATA]; /* ukupno 52 karte */
for (i = 0; i < BROJKARATA; i++)
karte[i] = i;
for (i = 0; i < BROJKARATA; i++)
{
int k = rand() % BROJKARATA;
swap (&karte[i], &karte[k]);
}
for (i = 0; i < BROJKARATA; i++)
printf("%s - %sn", boja[karte[i]/13], lik[karte[i]%13]);
return 0;
}
Dobije se ispis:
Pik - 3
Srce - 9
Tref - 10
Srce - 10
Tref - 5
Tref - 8
Tref - Kralj
. . . . .
Pik - 7
Srce - 3
Tref - Dama
Tref - Jack
Tref - 6
Karo - 8
156](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-156-320.jpg)

![srand((unsigned int)time(NULL));
Zadatak: Uvrstite prethodni iskaz u program karte.c (također, dodajte direktivu
#include<time.h>). Pokrenite program nekoliko puta i provjerite da li se pri svakom
izvršenju programa dobije drugačija podjela karata.
11.8 Argumenti komandne linije operativnog sustava
Funkcija main() također može imati argumente. Njoj argumente prosljeđuje operativni
sustav s komandne linije. Primjerice, pri pozivu kompilatora (c:>cl karte.c ) iz komandne linije
se kao argument prosljeđuje string koji sadrži ime datoteke koja se kompilira. Opći oblik
deklaracije funkcije main(), koja prima argumente s komandne linije, glasi:
int main( int argc, char *argv[])
Parametri su:
argc sadrži broj argumenata. Prvi argument (indeks nula) je uvijek ime samog programa,
dakle broj argumenata je uvijek veći ili jednak 1.
argv je niz pokazivača na char, svaki pokazuje na početni znak stringova koji su u
komandnoj liniji odvojeni razmakom.
Primjer: Programom cmdline.c ispituje se sadržaj komandne linije
/* Datoteka: cmdline.c */
#include <stdio.h>
int main( int argc, char *argv[])
{
int i;
printf("Ime programa je: %sn", argv[0]);
if (argc > 1)
for (i = 1; i < argc; i++)
printf("%d. argument: %sn", i, argv[i]);
return 0;
}
Ako se otkuca:
c:> cmdline Hello World
dobije su ispis:
Ime programa: C:CMDLINE.EXE
1. argument: Hello
2. argument: World
jer je:
argc = 3
argv[0] = "C:CMDLINE.EXE"
argv[1] = "Hello"
argv[2] = "World"
Primjer: Program cmdsum.c računa sumu dva realna broja koji se unose u komandnoj liniji iza
imena izvršnog programa. Primjerice, ako se u komandnoj liniji otkuca:
158](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-158-320.jpg)
![C:>cmdsum 6.5 4e-2
program treba dati ispis
Suma: 6.500000 + 0.040000 = 6.540000
/* Datoteka: cmdsum.c */
#include <stdio.h>
#include <stdlib.h>
int main( int argc, char *argv[])
{
float x,y;
if (argc > 2) /* unose se dva argumenta */
{
x = atof(argv[1]);
y = atof(argv[2]);
printf ("Suma: %f + %f = %fn", x, y, x+y);
}
else
printf("Otkucaj: cmdsum broj1 broj2 n");
return 0;
}
159](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-159-320.jpg)


![U programu allocarr.c alocira se niz od maxsize=5 cjelobrojnih elemenata. Korisnik
zatim unosi niz brojeva. Ako broj unesenih brojeva premaši maxsize, tada se povećava
alocirana memorija za dodatnih 5 elemenata. Unos se prekida kada korisnk otkuca slovo. Na
kraju se ispisuje niz i dealocira memorija.
/*Datoteka: allocarr.c*/
#include <stdio.h>
#include <stdlib.h>
void izlaz(char *string)
{
printf("%s", string);
exit(1);
}
int main( void )
{
int *pa ; /* pokazivač na niz cijelih brojeva */
int maxsize = 5; /* početna maksimalna veličina niza */
int num = 0; /* početno je u nizu 0 elemenata */
int j,data;
/*
* Početno alociraj memoriju za maxsize = 5 cijelih brojeva.
* Koristi funkciju malloc koji vraća pokazivač pa.
* Izvrši provjeru NULL vrijednosti pokazivača
*/
pa = malloc(maxsize * sizeof( int ));
if(pa == NULL )
izlaz("Nema slobodne memorije za malloc.n") ;
/*
* Učitaj proizvoljan broj cijelih brojeva u niz pa[]
* Ako broj premaši maxsize:
* povećaj allocirani niz za 5 elemenata pomoću funkcije realloc
* Kraj unosa je ako se umjesto broja pritisne neko slovo
*/
while(scanf("%d", &data) == 1)
{
pa[num++] = data; /* upisi podatak u memoriju */
if(num >= maxsize) /* ako je memorija popunjena */
{ /* povećaj alociranu memoriju */
maxsize += 5; /* za dodatnih 5 elemenata */
pa = realloc( pa, maxsize * sizeof(int));
if(pa== NULL)
izlaz("Nema slobodne memorije za realloc.n") ;
}
}
/* Ispiši podatke iz dinamički alociranog niza */
for(j = 0; j < num; j ++ )
printf("%d n", pa[j]) ;
/* Konačno vrati memoriju na heap koristeći free() */
free( pa ) ;
return 0 ;
}
162](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-162-320.jpg)
![Primjer: Pokazana je implementacija funkcije char * NumToString(int n), koja pretvara
cijeli broj n u string i vraća pokazivač na taj string.
char *NumToString( int n)
{
char buf[100], *ptr;
sprintf( buf, "%d", n);
ptr = malloc( strlen( buf) + 1);
strcpy( ptr, buf);
return ptr;
}
Primjer primjene funkcije NumToString:
char *s;
s = NumToString(56);
printf("%sn", s);
free(s); /* !!! oslobodi memoriju kad više ne trebaš s */
Napomena: Ako se u nekoj funkciji alocira memorija i pridijeli pokazivaču koji je lokalna
varijabla, nakon izlaza iz funkcije taj pokazivač više ne postoji (zašto?). Alocirana memorija će
i dalje postojati ukoliko nije prije završetka funkcije eksplicitno dealocirana funkcijom
free(). Može se dogoditi da ta memorija bude "izgubljena" ako je se ne dealocira, ili ako se iz
funkcije ne vrati pokazivač na tu memoriju (kao u slučaju funkcije NumToString).
Primjer: Funkciji char * strdup(char *s) namjena je da stvori kopiju nekog stringa s, i
vrati pokazivač na novoformirani string.
char *strdup( char * s)
{
char *buf, *ptr;
int n = strlen(s);
/* alociraj memoriju n+1 bajta za kopiju stringa s*/
buf = malloc(n* sizeof(char)+1);
/* kopiraj string u tu memoriju */
if(buf != NULL)
strcpy( buf, s);
/* vrati pokazivač na string */
return buf;
}
Ova funkcija nije specificirana u standardnoj biblioteci C jezika, ali je implementirana u
biblioteci Visual C i gcc kompilatora.
12.2 Kako se vrši alociranje memorije
Da bi se bolje shvatio proces alociranja memorije, bit će ilustrirano stanje slobodnje
memorije u slučaju kada se vrši višestruko alociranje/dealociranje memorije. Sivom bojom
označeno je područje slobodne memorije:
163](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-163-320.jpg)

![Kaže se da je slobodna memorija fragmentirana. Pri višestrukim pozivima malloc/free može
doći do višestruke fragmentacije, čime se "gubi" jedan dio slobodne memorije.
Zapamtite:
• O stanju slobodne memorije vodi računa posebni proces – memorijski alokator.
• Nakon što se alocira memorija pomoću funkcije malloc(), treba je inicijalizirati.
• Ako se želi inicijalizirati sadržaj memorije na vrijednost nula, koristi se funkcija
calloc().
• Ne smije se pretpostaviti da se sukcesivnim pozivima funkcije malloc() dobiva
kontinuirani memorijski blok.
12.3 Alociranje višedimenzionalnih nizova
Korištenje pokazivača i funkcija za dinamičko alociranja memorije omogućuje stvaranje
dinamičkih struktura podataka koje mogu imati promjenljivu veličinu tijekom izvršenja
programa. Nema posebnih pravila za stvaranje dinamičkih struktura podataka. U ovom i u
narednim poglavljima bit će pokazani različiti primjeri koji su korisni u programiranju i koji se
mogu koristiti kao obrazac za "dinamičko struktuiranje podataka" u C jeziku.
Najprije će biti opisano kako se dinamički alociraju višedimenzionalni nizovi i to nizovi
stringova i matrice promjenljivih dimenzija.
Dinamički nizovi stringova
Prije je pokazano da se u C jeziku pokazivači tipa char * mogu tretirati kao stringovi, uz uvjet
da pokazuju na niz znakova koji završava s nultim znakom. To omogućuje da se niz stringova
deklarira iskazom:
#define N 100
char *txt[N];
Ovaj niz stringova je statičan jer se njime može registrirati konačan broj stringova txt[i].
Uočite da je N konstanta.
Niz stringova se može realizirati i dinamičkim alociranjem niza koji će sadržavati N
pokazivača tipa char *. To se postiže iskazima:
int N = 100; /* veličina niza je varijabla */
char **txt; /* txt pokazuje na niz pokazivača */
txt = calloc(N, sizeof(char*)); /* alociraj za N pokazivača */
U oba slučaja txt[i] predstavlja string. Razlika je pak od prethodne definicije niza stringova u
tome što se sada veličina niza može mijenjati tijekom izvršenja programa. Početno su svi
elementi niza jednaki NULL, što znači da niz nije inicijaliziran. Inicijalizacija niza se postiže
tako da se pokazivačima txt[i] pridijeli adresa nekog stringa. Primjerice, nakon sljedećih
operacija:
txt[0]= strdup("Hello")
txt[1]= strdup("World!")
txt[2]= strdup("je prvi C program")
prva tri elementa niza txt[i] predstavljaju stringove, a ostali elementi niza su i dalje
neinicijalizirani.
Stanje u memoriji se može ilustrirati slikom 12.2.
165](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-165-320.jpg)
![Slika 12.2 Prikaz korištenja memorije za dinamički niz stringova
Nakon upotrebe, potrebno je osloboditi memoriju koju zauzima niz stringova. To se postiže
tako da se najprije dealocira memorija koju zauzimaju stringovi.
for(i=0; i<N; i++) {
if(txt[i] != NULL) /* oslobodi samo alocirane stringove */
free(txt[i]);
}
a zatim se dealocira memorija koju zauzima niz pokazivača txt;
free(txt);
Prikazana struktura je zgodna za unošenje proizvoljnog broja linija teksta, i može biti
temeljna struktura u editoru teksta. U ovu strukturu je lako unositi tekst , brisati tekst i
povećavati broj linija teksta.
Primjer: U programu alloctxt.c korisnik unosi proizvoljan broj linija teksta. Početno se
alocira memorija za 5 linija teksta. Ako korisnik unese više linija, tada se pomoću funkcije
realloc() povećava potrebna memorija za dodatnih 5 linija. Unos završava kada se otkuca
prazna linija. Nakon toga se vrši sortiranje teksta pomoću funkcije qsort(). Na kraju
programa ispisuje se sortirani tekst i dealocira memorija.
/* Datoteka: alloctxt.c */
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int CmpString( const void *pstr1, const void *pstr2 );
char *strdup( char * s);
void memerror();
int main( void )
{
char **txt; /* pokazivač na pokazivač stringa */
int maxsize = 5; /* početna maksimalna veličina niza */
int numstrings = 0; /* početno je u nizu 0 stringova */
char str[256]={"0"};
166](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-166-320.jpg)
![int i;
/*
* Početno alociraj memoriju za maxsize=5 ,
* Koristi malloc koji vraća pokazivač u txt.
* Izvrši provjeru NULL vrijednosti pokazivača
*/
txt = malloc(maxsize * sizeof(char *));
if(txt == NULL ) memerror() ;
/*
* Učitaj proizvoljan broj stringova u niz txt[]:
* Prethodno alociraj memoriju sa svaki uneseni string
* Ako broj stringova premaši maxsize:
* povećaj allocirani niz za 5 elemenata pomoću funkcije realloc
* Kraj unosa je ako se unese prazna linija.
*/
while(gets(str) != NULL)
{
char *s = strdup( str) ;
if(s== NULL) memerror();
if(strlen(s)==0)
break;
txt[numstrings++] = s;
if(numstrings >= maxsize)
{
maxsize += 5;
txt = realloc( txt, maxsize * sizeof( int ));
if(txt== NULL) memerror();
}
}
/* sortiraj niz stringova leksikografski */
if(numstrings > 1)
qsort((void *)txt, numstrings, sizeof(char*), CmpString);
/* Ispiši podatke iz dinamički alociranog niza
* i vrati memoriju na heap koristeći free()
* za svaki pojedinačni string
*/
for(i = 0; i < numstrings; i ++ )
{
puts(txt[i]) ;
free( txt[i] );
}
free(txt);
return 0 ;
}
int CmpString( const void *pstr1, const void *pstr2 )
{
/* Ova usporedna funkcija se koristi u funkciji qsort()
* Prema dogovoru, u usporednu funkciju se šalju pokazivači
* na element niza, u ovom slučaju
* pokazivac na string, odnosno char **.
167](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-167-320.jpg)
![* Za usporedbu stringova koristi se funkcija strcmp().
* Pošto argument funkcije strcmp mora biti string (char *)
* to znači da joj se mora poslati *pstr1 i *pstr2,
* odnosno sadržaj argumenata pstr1 i pstr2,
* koji su pokazivaci tipa char**
*/
return strcmp( *(char **) pstr1, *(char **)pstr2 );
}
void memerror()
{ /* funkcija za dojavu pogreške */
printf("%s", "Greska pri alociranju memorije");
exit(1);
}
Dinamičke matrice
Matrica je skup istovrsnih elemenata koji se obilježavaju s dva indeksa - mat[i][j]. Prvi
indeks predstavlja redak, a drugi indeks predstavlja stupac matrice. Matrica se može
programski realizirati kao dinamička struktura. Primjerice, matrica imena mat, koja će
sadržavati elemente tipa double, se sljedećim postupkom:
Slika 12.3 Prikaz korištenja memorije za dinamičke matrice
1. Identifikator matrice se deklarira kao pokazivač na pokazivač na double, a dvije varijable
koje označavaju broj redaka i stupaca matrice se iniciraju na neku početnu vrijednost.
int brojredaka = 5, brojstupaca=10;
double **mat;
2. Alocira se memorija za niz pokazivača na retke matrice (mat[i])
mat = malloc( brojredaka * sizeof(double *));
3. Zatim se alocira memorija za svaki pojedini redak. To zauzeće je određeno brojem stupaca
matrice:
for(k = 0; k < brojredaka; k++)
mat[i] = malloc( brojstupaca * sizeof(double));
4. Ovime je postupak formiranja matrice završen. Nakon toga se mogu raditi operacije s
matricom. Primjerice, iskaz
for(i = 0; i < brojredaka; i++)
for(j = 0; j < brojstupaca; j++)
mat[i][j] = 0;
168](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-168-320.jpg)
![postavlja sve elemente matrice na vrijednost nula.
5. Nakon završetka rada s matricom potrebno je osloboditi alociranu memoriju. To se postiže
tako da se najprije dealocira memorija koju zauzimaju elementi matrice;
for(k=0; k < brojredaka; k++)
free(mat[k]);
a zatim se dealocira memorija koju zauzima niz pokazivača retka;
free(mat);
Iako ovaj postupak izgleda dosta kompliciran, on se često koristi jer se njime omogućuje rad s
matricama čije se dimenzije mogu mijenjati tijekom izvršenja programa. Također, pogodno je
pisati funkcije s ovakvim matricama, jer se mogu primijeniti na matrice proizvoljnih dimenzija.
Primjerice, funkcija:
void NulMat(double **mat, int brojredaka, int brojstupaca)
{
for(int i = 0; i < brojredaka; i++)
for(int j = 0; j < brojstupaca; j++)
mat[i][j] = 0;
}
može poslužiti da se postavi vrijednost elemenata bilo koje matrice na vrijednost 0. Ovo nije
moguće kod korištenja statičkih nizova je se tada u definiciji funkcije, u parametru koji
označava dvodimenzionalni niz, uvijek mora označiti broj kolona.
Funkcija PrintMat() može poslužiti za ispis matrice u proizvoljnom formatu:
void PrintMat(double **mat, int brojredaka,
int brojstupaca, char *format)
{
int i,j;
for( i = 0; i < brojredaka; i++)
{
for(j = 0; j < brojstupaca; j++)
printf (format, mat[i][j]);
printf("n") ;
}
}
Sam postupak alociranja i dealociranja matrice se može formalizirati s dvije funkcije
double **AlocirajMatricu (int brojredaka,int brojstupaca)
{
int k;
double **mat = malloc( brojredaka * sizeof(double *));
if(mat == NULL) return NULL;
for(k = 0; k < brojredaka; k++)
mat[k] = malloc( brojstupaca * sizeof(double));
return mat;
}
void DealocirajMatricu(double **mat, int brojredaka)
169](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-169-320.jpg)
![{
int k;
for(k=0; k < brojredaka; k++)
free(mat[k]);
free(mat);
}
Primjer: U programu allocmat.c formira se matrica s 3x4 elementa, ispunja slučajnim
brojem i ispisuje vrijednost elemenata matrice. Zatim se ta matrica dealocira i ponovo alocira s
2x2 elementa.
/* Datoteka: allocmat.c */
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
double **AlocirajMatricu (int brojredaka,int brojstupaca);
void DealocirajMatricu(double **mat, int brojredaka);
void PrintMat(double **mat, int brojredaka, int brojstupaca, char
*format);
int main( void )
{
int i,j;
double **mat; /* matrica */
int rd= 3; /* broj redaka */
int st= 4; /* broj stupaca */
/* formiraj matricu sa 3x4 elementa*/
mat = AlocirajMatricu(rd, st);
if(mat == NULL) exit(1);
/* ispuni matricu sa slučajnim vrijednostima */
for(i = 0; i < rd; i++)
for(j = 0; j < st; j++)
mat[i][j] = (double)rand();
/* ispisi vrijednosti */
PrintMat(mat, rd, st, "%12.2lf");
DealocirajMatricu(mat, rd);
/* sada formiraj drugu matricu sa 2x2 elementa*/
rd = 2; st = 2;
mat = AlocirajMatricu(rd, st);
if(mat == NULL) exit(1);
for(i = 0; i < rd; i++)
for(j = 0; j < st; j++)
mat[i][j] = (double)rand();
/* ispisi vrijednosti */
PrintMat(mat, rd, st, "%12.2lf");
DealocirajMatricu(mat, rd);
return 0 ;
170](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-170-320.jpg)
![}
/* definiraj potrebne funkcije */
Dobije se ispis:
41.00 18467.00 6334.00 26500.00
19169.00 15724.00 11478.00 29358.00
26962.00 24464.00 5705.00 28145.00
23281.00 16827.00
9961.00 491.00
12.4 Standardne funkcije za brzi pristup memoriji
U standardnoj biblioteci je definirano nekoliko funkcija koje su optimirane za brzi pristup
memoriji.
void *memcpy(void *d, const void *s, size_t n)
Kopira n znakova s adrese s na adresu d, i vraća d.
void *memmove(void *d, const void *s, size_t n)
Ima isto djelovanje kao memcpy, osim što vrijedi i za preklapajuća memorijska područja.
int memcmp(const void *s, const void *t, size_t n)
uspoređuje prvih n znakova s i t; vraća rezultat kao strcmp.
void *memchr(const void *m, int c, size_t n)
vraća pokazivač na prvu pojavu znaka c u memorijskom području m, ili NULL ako znak nije
prisutan među prvih n znakova.
void *memset(void *m, int c, size_t n)
postavlja znak c u prvih n bajta od m , vraća m.
Primjer: prethodnu funkciju NulMat() može se napisati pomoću memset() funkcije:
void NulMat(double **mat, int brojredaka, int brojstupaca)
{
for(int i = 0; i < brojredaka; i++)
memset(mat[i], 0, brojstupaca*sizeof(double)
}
171](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-171-320.jpg)



![Ako se struktura inicijalizira djelomično, elementi koji nisu inicijalizirani se postavljaju na
vrijednost nula.
Strukture i nizovi
Elementi strukture mogu biti nizovi. Također, može se formirati nizove struktura.
Primjerice, struktura za vođenje evidencije o ocjenama pojedinog studenta može imati oblik:
typedef struct _studentinfo
{
char ime[30];
int ocjena;
} studentinfo_t;
Uz pretpostavku da nastavu pohađa 30 studenata, za vođenje evidencije o studentima može se
definirati niz:
studentinfo_t student[30];
Pojedinom članu strukture, koji je element niza, pristupa se na način da se točka operator piše
iza uglatih zagrada, primjerice:
student[0].ocjena = 2;
student[1].ocjena = 5;
Struktura kao argument funkcije
Strukture se, za razliku od nizova, tretiraju kao "tipovi prve klase". To znači da se može
pridijeliti vrijednost jedne strukturne varijable drugoj, da se vrijednost strukturne varijable može
prenositi kao argument funkcije i da funkcija može vratiti vrijednost strukturne varijable.
Program struct.c demonstrira upotrebu strukturnih varijabli u argumenatima funkcije.
/* Datoteka: struct.c */
/* Primjer definiraja strukture i koristenja */
/* strukture kao argumenta funkcije */
#include <stdio.h>
#include <string.h>
typedef struct _student
{
char ime[30];
int ocjena;
}studentinfo_t;
void display( studentinfo_t st );
int main()
{
studentinfo_t student[30];
int i=0;
strcpy( student[0].ime, "Marko Matic" );
student[0].ocjena = 4;
strcpy( student[1].ime, "Marko Katic" );
student[1].ocjena = 2;
strcpy( student[2].ime, "Ivo Runjanin" );
student[2].ocjena = 1;
175](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-175-320.jpg)
![strcpy( student[3].ime, "" );
student[3].ocjena = 0;
while (student[i].ocjena != 0 )
display( student[i++]);
return 0;
}
void display(studentinfo_t st)
{
printf( "Ime: %s ", st.ime );
printf( "tocjena: %dn", st.ocjena );
}
Rezultat izvršenja programa je:
Ime: Marko Matic ocjena: 4
Ime: Marko Katic ocjena: 2
Ime: Ivo Runjanin ocjena: 1
U programu se prvo inicijalizira prva tri elementa niza koji su tipa studentinfo_t.
Četvrtom elementu se vrijednost člana ocjena postavlja na vrijednost nula. Ova nulta ocjena će
kasnije služiti kao oznaka elementa niza, do kojeg su uneseni potpuni podaci. Ispis se vrši
pomoću funkcije display(studentinfo_t).
U prethodnom programu strukturna varijabla se prenosi u funkciju po vrijednosti. Ovaj
način prijenosa strukture u funkciju nije preporučljiv jer se za prijenos po vrijednosti na stog
mora kopirati cijeli sadržaj strukture. To zahtijeva veliku količinu memorije i procesorskog
vremena (u ovom slučaju veličina strukture je 34 bajta). Mnogo bolji način prijenosa strukture u
funkciju je da se koristi pokazivač na strukturu, a da se zatim u funkciji elementima strukture
pristupa indirekcijom.
Pokazivači na strukturne tipove i operator ->
Neka su deklarirani varijabla i pokazivač tipa studentinfo_t:
studentinfo_t St, *pSt;
i neka je varijabla St inicijalizirana slijedećim iskazom:
St.ime = strcpy("Ivo Boban");
St.ocjena = 1;
Ako se pokazivač pSt inicijalizira na adresu varijable St, tj.
pSt = &St;
tada se može pristupiti varijabli St i pomoću dereferenciranog pokazivača. Primjerice, ako se
želi promijeniti ocjenu na vrijednost 2 i ispisati novo stanje, može se koristiti iskaze:
(*pSt).ocjena = 2;
printf("Ime: %s, ocjena: %d", (*pSt).ime, (*pSt).ocjena)
Uočite da se zbog primjene točka operatora dereferencirani pokazivač mora napisati u
zagradama, jer bi inače točka operator imao prioritet. Ovakav način označavanja indirekcije je
dosta kompliciran, stoga je u C jeziku definiran operator ->, pomoću kojeg se prethodni iskazi
zapisuju u obliku:
176](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-176-320.jpg)
![pSt->ocjena = 2;
printf("Ime: %s, ocjena: %d", pSt->ime, pSt->ocjena)
Vrijedi ekvivalentni zapis
(*pStudent).ocjena ⇔ pStudent->ocjena
Operator -> označava pristup elementu strukture pomoću pokazivača i može ga se
zvati operatorom indirekcije pokazivača strukture.
Primjer: U programu structp.c pokazano je kako se prethodni program može napisati
mnogo efikasnije korištenjem pokazivača. U ovom primjeru pokazivači će se koristiti i kao
članove strukture i pomoću njih će se vršiti prijenos strukturne varijable u funkciju.
/* Datoteka: structp.c
* Primjer definiraja strukture pomocu pokazivačkih članova i
* korištenje pokazivača strukture kao argumenta funkcije
*/
#include <stdio.h>
#include <stdlib.h> /* def. NULL */
typedef struct _student
{
char *ime;
int ocjena;
}studentinfo_t;
void display( studentinfo_t *pSt );
int main()
{
int i=0;
studentinfo_t *p;
studentinfo_t student[30] = {
{ "Marko Matic", 4 },
{ "Marko Katic", 2 },
{ "Ivo Runjanin", 1 },
{ NULL, 0}
};
p=&student[0];
while (p->ime != NULL )
display( p++);
return 0;
}
void display(studentinfo_t *pS)
{
printf( "Ime: %s ", pS->ime );
printf( "tocjena: %dn", pS->ocjena );
}
177](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-177-320.jpg)
![Prvo što se treba uočiti u ovom programu je način kako je deklarirana struktura _student . U
njoj sada nije rezerviran fiksni broj mjesta za član ime, već ime sada predstavlja pokazivač na
char (string).
typedef struct _student
{
char *ime;
int ocjena;
}studentinfo_t;
Niz student je inicijaliziran pri samoj deklaraciji sa:
studentinfo_t student[30] = {
{ "Marko Matic", 4 },
{ "Marko Katic", 2 },
{ "Ivo Runjanin", 1 },
{ NULL, 0}
};
Ovime se postiže ušteda memorije jer se za string ime rezervira točno onoliko mjesta koliko
je upisano inicijalizacijom (plus nula!). Pomoćnim pokazivačem p, kojeg se početno inicira na
adresu nultog elementa niza student, pretražuje se niz sve dok se ne dođe do elementa kojem
član ime ima vrijednost NULL pokazivača. Dok to nije ispunjeno vrši se ispis sadržaja niza
pomoću funkcije display(), kojoj se kao argument prenosi pokazivač na tip
studentinfo_t. Unutar funkcije display() elementima strukture se pristupa indirekcijom
pokazivača strukture (->).
Na kraju, da se zaključiti, da prijenos strukture u funkciju u pravilu treba vršiti pomoću
pokazivača. Isto vrijedi za slučaj kada funkcija vraća vrijednost strukture. I u tom slučaju je
bolje raditi s pokazivačima na strukturu, jer se štedi memorija i vrijeme izvršenja programa.
Prenošenje strukture po vrijednosti se može tolerirati samo u slučajevima kada struktura ima
malo zauzeće memorije.
Memorijska slika strukturnih tipova
U tablici 13.1 dana je usporedba karakteristika nizova i struktura. Važno je uočiti da
članovi struktura u memoriji nisu nužno poredani neposredno jedan do drugog. Razlog tome je
činjenica da je dozvoljeno da se članovi strukture smještaju u memoriju na način za koji se
ocjenjuje da će dati najbrže izvršenje programa (većina procesora brže pristupa parnim
adresama, nego neparnim adresama).
karakteristika niz struktura
strukturalni sadržaj kolekcija elemenata istog tipa kolekcija imenovanih članova koji
mogu biti različitog tipa
pristup elementima elementima se pristupa članovima se pristupa pomoću imena
složenog tipa pomoću indeksa niza
raspored elemenata u u nizu jedan do drugog u nizu, ali ne nužno jedan do drugog
memoriji računala
Tablica 13.1. Usporedba nizova i struktura
Kod kompilatora Microsoft Visual C može se posebnom direktivom (#pragma pack(1))
zadati da se članovi strukture "pakiraju" u memoriju jedan do drugog. To pokazuje program
pack.c.
178](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-178-320.jpg)






![%w broj za dan u sedmici (0-nedjelja)
%W broj za sedmicu u godini (1..52) - 1 određen prvim ponedjeljkom
%x kompletni zapis datuma
%X kompletni zapis vremena
%y zadnje dvije znamenke godine
%Y godina u formatu s 4 znamenke
%Z ime vremenske zone (ako postoji )
%% znak %
Primjer: U programu vrijeme.c demonstrira se korištenje funkcija za datum i vrijeme.
/* Datoteka: vrijeme.c */
/* Prikazuje datum i vrijeme u tri formata*/
#include <stdio.h>
#include <time.h>
int main()
{
time_t vrijeme = time(NULL);
struct tm *ptr;
char datum_str[20];
/* ispisuje datum i vrijeme u standardnom formatu */
puts(ctime(&vrijeme));
/* ispisuje datum i vrijeme pomoću strftime funkcije */
strftime(datum_str, sizeof(datum_str),
"%d.%m.%y %H:%Mn", localtime(&vrijeme));
puts(datum_str);
/* ispisuje datum i vrijeme u proizvoljnom formatu */
ptr = localtime(&vrijeme);
printf("%.2d.%.2d.%.2d %2d:%.2dn",
ptr->tm_mday, ptr->tm_mon+1, ptr->tm_year +1900,
ptr->tm_hour, ptr->tm_min);
return 0;
}
Dobije se ispis:
Mon May 13 20:13:06 2002
13.05.02 20:13
13.05.2002 20:13
Za obradu vremena se koriste i sljedeće funkcije:
mktime
time_t mktime(struct tm *tp)
Funkcija mktime() pretvara zapisa iz strukture tm u time_t format. Korisna je u tzv.
kalendarskim proračunima. Kada je potrebno dodati nekom datumu n dana, tada se može upisati
185](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-185-320.jpg)





![sin = 0.14112
cos = -0.989992
Operator ## djeluje na dva susjedna simbola na način da preprocesor izbaci taj operator i
sva prazna mjesta, pa se dobije jedan novi simbol s identifikatorom sastavljenim od ta dva
susjedna simbola. Primjerice, za definiciju
#define NIZ(ime, tip, n) tip ime ## _array_ ## tip[N]
vrši se ekspanzija
NIZ(x, int, 100) int x_array_int [100]
NIZ(vektor, double, N) double vektor_array_double [N]
Zadatak: Provjerite ispis sljedećeg programa:
/* program strop.c */
#include <stdio.h>
#define N 10
#define PRINT(x) printf(#x "=%dn", x)
#define NIZ(ime, tip, n) tip ime ## _array [n]
int main()
{
int i, y=7;
NIZ(x, int, N);
for(i=0; i<N;i++) x_array[i] = 10;
PRINT(y);
PRINT(x_array[y]);
return 0;
}
Ispis je:
y=7
x_array[y]=10
14.4 Direktiva #undef
Ponekad je potrebno redefinirati značaj nekog identifikatora. U tu svrhu koristi se direktiva
#undef:
#undef identifikator
Ovom se direktivom poništava prethodni značaj identifikatora. Primjerice,
#define SIMBOL_X VALUE_FOR_X
....
.... /* područje gdje se koristi SIMBOL_X */
....
191](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-191-320.jpg)






![/* 5 realnih brojeva, koje unosi korisnik */
#include <stdlib.h>
#include <stdio.h>
int main()
{
FILE *fp;
float data[5];
int i;
char filename[20];
puts("Otipkaj 5 realnih brojeva");
for (i = 0; i < 5; i++)
scanf("%f", &data[i]);
/* Dobavi ime datoteke, ali prethodno */
/* isprazni moguci višak znakova iz međuspremnika ulaza */
fflush(stdin);
puts("Otipkaj ime datoteka:");
gets(filename);
if ( (fp = fopen(filename, "w")) == NULL)
{
fprintf(stderr, "Greska pri otvaranju datoteke %s.",
filename);
exit(1);
}
/*Ispisi vrijednosti u datoteku i na standardni izlaz */
for (i = 0; i < 5; i++)
{
fprintf(fp, "ndata[%d] = %f", i, data[i]);
fprintf(stdout, "ndata[%d] = %f", i, data[i]);
}
fclose(fp);
printf("nSada procitaj datoteku: %s, nekim editorom",
filename);
return(0);
}
Izlaz iz programa je:
Otipkaj 5 realnih brojeva
3.14159
9.99
1.50
3.
1000.01
Otipkaj ime datoteke
brojevi.txt
data[0] = 3.141590
data[1] = 9.990000
data[2] = 1.500000
data[3] = 3.000000
198](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-198-320.jpg)
![data[4] = 1000.010
Sada procitaj datoteku: brojevi.txt, nekim editorom
15.5 Formatirano čitanje podataka iz datoteke
Za formatirano čitanje sadržaja datoteke koristi se fscanf() funkcija, koja je poopćeni
oblik scanf() funkcije za dobavu podataka iz ulaznih tokova. Prototip fscanf() funkcije je:
int fscanf(FILE *fp, const char *fmt, ...);
Parametar fp je pokazivač ulaznog toka, koji može biti stdout ili datotečni tok koji se dobije
kada se datoteka otvori s atributom "r", "r+" ili "w+". String fmt služi za specifikaciju formata
po kojem se učitava vrijednost varijabli, čije adrese se koriste kao argumenti funkcije. Tri točke
označavaju proizvoljan broj argumenata, uz uvjet da svakom argumentu mora pripadati po jedan
specifikator formata u stringu fmt.
Primjer: Program txtfile-read.c čita sadržaj datoteke "input.txt", a zatim ga ispisuje na
standardni izlaz. Prethodno je potrebno nekim editorom teksta formirati datoteka imena
"input.txt", sa sljedećim sadržajem:
6.8 5.89
67
1.099010
67.001
/* Datoteka: txtfile-read.c */
/* Demonstrira se upis u tekstualnu datotke */
/* 5 realnih brojeva, koje unosu korisnik */
#include <stdio.h>
int main()
{
float f1, f2, f3, f4, f5;
FILE *fp;
if ( (fp = fopen("INPUT.TXT", "r")) == NULL)
{
fprintf(stderr, "Greska pri otvaranju datoteke.n");
exit(1);
}
fscanf(fp, "%f %f %f %f %f", &f1, &f2, &f3, &f4, &f5);
fprintf(stdout, "Vrijednosti u datoteci su:n");
fprintf(stdout, "%f, %f, %f, %f, %fn.", f1, f2, f3, f4, f5);
fclose(fp);
return(0);
}
Ispis je:
Vrijednosti u datoteci su:
6.800000, 5.890000, 67.000000, 1.099010, 67.000999
199](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-199-320.jpg)


![int kopiraj_datoteke( char *ime_izvora, char *ime_odredista );
Funkcija prima dva argumenta koji označavaju imena izvorne i odredišne datoteke. Vraća 0 ako
nije izvršeno kopiranje ili 1 ako je kopiranje uspješno. Implementacija funkcije je:
int kopiraj_datoteke( char *ime_izvora, char *ime_odredista )
{
FILE *fpi, *fpo;
/* Otvori datoteku za čitanje u binarnom modu */
if (fpi = fopen( ime_izvora, "rb" ) == NULL )
return 0;
/* Otvori datoteku za pisanje u binarnom modu */
if ( fpo = fopen( ime_odredista, "wb" ) == NULL )
{
fclose ( fpi );
return 0;
}
/* Učitaj 1 bajt iz fpi. Ako nije eof, upiši bajt u fpo */
while (1)
{
char c = fgetc( fpi );
if ( !feof( fpi ) )
fputc( c, fpo );
else
break;
}
fclose ( fpi);
fclose ( fpo);
return 1;
}
Testiranje ove funkcije se provodi programom kopiraj.c u kojem se ime izvorne i odredišne
datoteke dobavlja s komandne linije.
/* Datoteka: kopiraj.c
* kopira datoteku ime1 u datoteku ime2, komandom
* c:> kopiraj ime1 ime2
*/
#include <stdio.h>
int kopiraj_datoteke( char *ime_izvora, char *ime_odredista );
int main(int argc, char **argv)
{
char *ime1, *ime2;
if (argc <3) /* moraju biti dva argumenta komandne linije */
{
printf("Uputstvo: kopiraj ime1 ime2n");
return 1;
}
ime1 = argv[1];
ime1 = argv[2];
if( kopiraj_datoteke(ime1, ime1 ) )
202](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-202-320.jpg)
![puts("Kopiranje zavrseno uspjesnon");
else
puts("Kopiranje neuspjesno!n");
return(0);
}
U radu s binarnim datotekama za detekciju kraja datoteke isključivo se koristi
funkcija feof(), dok se u radu s tekstualnim datotekama kraj datoteke može
detektirati i kada funkcije vrate EOF (obično je to vrijednost -1).
15.7 Direktni ulaz/izlaz za memorijske objekte
Najefikasniji i najbrži način pohrane bilo kojeg složenog memorijskog objekta je da se
zapisuje u binarne datoteke. Na taj način datoteka sadrži sliku memorijskog objekta, pa se isti
može na najbrži mogući način prenijeti iz datoteke u memoriju.
Za ovakvi tip ulazno izlaznih operacija predviđene su dvije funkcije: fwrite() i fread().
fwrite
Funkcija fwrite() služi za zapis u datoteku proizvoljnog broja bajta s neke memorijske
lokacije. Prototip funkcije je:
int fwrite(void *buf, int size, int count, FILE *fp);
Argument buf je pokazivač na memorijsku lokaciju s koje se podaci zapisuju u tok fp.
Argument size označava veličinu u bajtima pojedinog elementa koji se upisuje, a argument
count označava ukupni broj takovih elemenata koji se zapisuju. Primjerice, ako je potrebno
zapisati 100 elemenata niza cijelih brojeva, tada je size jednak 4 (sizeof int), a count je
jednako 100. Dakle, ukupno se zapisuje 400 bajta.
Funkcija vraća vrijednost koja je jednaka broju elemenata koji su uspješno zapisani. Ako je ta
vrijednost različita od count, to znači da je nastala pogreška. Uobičajeno je da se pri svakom
transferu vrši ispitivanje ispravnog transfera iskazom:
if( (fwrite(buf, size, count, fp)) != count)
fprintf(stderr, "Error writing to file.");
Primjeri korištenja funkcije fwrite():
1. zapis skalarne varijable x, koja je tipa float, vrši se sa:
fwrite(&x, sizeof(float), 1, fp);
2. zapis niza od 50 elemenata strukturnog tipa, primjerice
struct tocka {int x, int y;} niz[50];
vrši se iskazom:
fwrite(niz, sizeof(struct tocka), 50, fp);
ili fwrite(niz, sizeof(niz), 1, fp);
U drugom slučaju čitav se niz tretira kao jedan element, a učinak je isti kao u prvom iskazu.
203](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-203-320.jpg)
![fread
Funkcija fread() služi za učitavanje proizvoljnog broja bajta na neku memorijsku
lokaciju. Prototip funkcije je:
int fread(void *buf, int size, int count, FILE *fp);
Argument buf je pokazivač na memorijsku lokaciju u koju se upisuju podaci iz toka fp.
Argument size označava veličinu u bajtima pojedinog elementa koji se učitava, a argument
count označava ukupni broj takovih elemenata koji se učitavaju u memoriju.
Funkcija vraća vrijednost koja je jednaka broju elemenata koji su uspješno učitani. Ako je ta
vrijednost različita od count, to znači da je nastala greška ili je dosegnut kraj datoteke.
Primjer: U programu binio.c niz od 10 cijelih brojeva prvo se zapisuje u binarnu datoteku
imena "podaci", a zatim se taj niz ponovo učitava u binarnom obliku.
/*Datoteka: binio.c */
#include <stdlib.h>
#include <stdio.h>
#define SIZE 10
void prekini(char *s)
{
fprintf(stderr, s);
exit(1);
}
int main()
{
int i, niz1[SIZE], niz2[SIZE];
FILE *fp;
for (i = 0; i < SIZE; i++)
niz1[i] = 7 * i;
/* otvori datoteku za pisanje u binarnom modu*/
if ( (fp = fopen("podaci", "wb")) == NULL)
prekini("Greška pri otvaranju datoteke");
/* Spremi niz1 u datoteku */
if (fwrite(niz1, sizeof(int), SIZE, fp) != SIZE)
prekini("Greška pri pisanju u datoteku");
/* Zatvori datoteku */
fclose(fp);
/* Ponovo otvori datoteku za čitanje*/
if ( (fp = fopen("podaci", "rb")) == NULL)
prekini("Greška pri otvaranju datoteke");
/* Čitaj iz datoteke u niz2 */
if (fread(niz2, sizeof(int), SIZE, fp) != SIZE)
prekini("Greška pri citanju datoteke");
fclose(fp);
/* Sada ispisi oba niza i provjeri da li su jednaka*/
204](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-204-320.jpg)
![for (i = 0; i < SIZE; i++)
printf("%dt%dn", niz1[i], niz2[i]);
return(0);
}
Dobije se ispis:
0 0
7 7
14 14
21 21
28 28
35 35
42 42
49 49
56 56
63 63
Prednost zapisa u binarnom modu u odnosu na formatirani zapis nije samu u
efikasnom korištenju resursa i brzini rada. U binarnom modu nema gubitka
informacije (smanjenja točnosti numeričkih zapisa) koje se javljaju u formatiranom
zapisu.
Nije preporučljivo direktno zapisivanje u datoteku struktura koji sadrže
pokazivačke članove, jer pri ponovnom učitavanju takovih struktura pokazivači
neće sadržavati ispravne adrese.
Funkcije rewind() i ftell()
U prethodnom programu bilo je potrebno dva puta otvoriti i zatvoriti datoteku istog imena.
U oba slučaja se čitanje/pisanje vršilo od početka datoteke. U slučaju kada se s nekom
datotekom vrši čitanje i pisanje ona se može otvoriti u modu "w+b". Da bi ovi procesi startali od
početka datoteke tada je potrebno koristiti funkciju rewind() kojom se mjesto pristupa
datoteci postavlja na početak datoteke. Prototip ove funkcije glasi:
void rewind(FILE *fp);
Uvijek se može odrediti mjesto na kojem će biti izvršen slijedeći pristup datoteci. To se postiže
funkcijom ftell() kojoj je prototip:
long ftell(FILE *fp);
Funkcija ftell() vraća cjelobrojnu vrijednost koja odgovara poziciji (u bajtima) slijedećeg
pristupa datoteci. U slučaju pogreške funkcija vraća vrijednost -1L.
Primjer: Program binio1.c ima isti učinak kao i program binio.c, ali se koristi mod "w+b"
i funkcija rewind(). Također, demonstrira se upotreba funkcije ftell().
/*Datoteka: binio1.c */
#include <stdlib.h>
#include <stdio.h>
#define SIZE 10
205](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-205-320.jpg)
![void prekini(char *s)
{
fprintf(stderr, s);
exit(1);
}
int main()
{
int i, niz1[SIZE], niz2[SIZE];
FILE *fp;
for (i = 0; i < SIZE; i++)
niz1[i] = 7 * i;
/* Otvori datoteku za čitanje i pisanje*/
if ( (fp = fopen("podaci", "w+b")) == NULL)
prekini("Greška pri otvaranju datoteke");
/* Spremi niz1 u datoteku */
if (fwrite(niz1, sizeof(int), SIZE, fp) != SIZE)
prekini("Greška pri pisanju u datoteku");
/* pomoću ftell() izvijesti o broju bajta u datoteci */
printf("U datoteci je zapisano %d bajtan", ftell(fp));
/* vrati poziciju pristupa datoteci na pocetak */
rewind(fp);
/* Čitaj iz datoteke u niz2 */
if (fread(niz2, sizeof(int), SIZE, fp) != SIZE)
prekini("Greška pri citanju datoteke");
fclose(fp);
/* Sada ispisi oba niza i provjeri da li su jednaka*/
for (i = 0; i < SIZE; i++)
printf("%dt%dn", niz1[i], niz2[i]);
return(0);
}
15.8 Sekvencijani i proizvoljni pristup datotekama
Sekvencijalni pristup datoteci označava operacije s datotekama u kojima se čitanje ili
pisanje uvijek vrši na kraju datoteke. Proizvoljni ili slučajni pristup datoteci (random access)
označava operacije s datotekama u kojima se čitanje ili pisanje može usmjeriti na proizvoljno
mjesto u datoteci.
Svakoj se otvorenoj datoteci dodjeljuje jedan pozicijski indikator koji označava poziciju (u
bajtima) od početka datoteke na kojoj će biti izvršeno čitanje ili pisanje. U svim dosadašnjim
primjerima korišten je sekvencijalni pristup datoteci. U tom slučaju, nakon otvaranja datoteke
pozicijski indikator ima vrijednost 0, a kada se datoteka zatvori pozicijski indikator ima
vrijednost koja je jednaka broju bajta koji su zapisani u datoteci, ukoliko je posljednja operacija
bila pisanje u datoteku.
Proizvoljni pristup datoteci ima smisla samo kod binarnih datoteka, kod kojih se čitanje i
pisanje vrši kontrolirano bajt po bajt. On se ostvaruje pomoću funkcije fseek().
fseek
Funkcija fseek() služi za proizvoljno postavljanje pozicijskog indikatora datoteke.
Deklarirana je u datoteci <stdio.h> prototipom:
206](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-206-320.jpg)
![int fseek(FILE *fp, long pomak, int seek_start);
Prvi argument je pokazivač toka. Drugi argument određuje pomak pozicijskog indikatora, a
treći argument određuje od koje startne pozicije se vrši pomak pozicijskog indikatora. Ova
startna pozicija se određuje pomoću tri konstante koje su definirane u <stdio.h>, a njihov
značaj je opisan u tablici:
Konstanta Vrijednost Značaj vrijednosti seek_start
SEEK_SET 0 Pomak se vrši od početka datoteke prema kraju datoteke.
SEEK_CUR 1 Pomak se vrši od trenutne pozicije prema kraju datoteke.
SEEK_END 2 Pomak se vrši od kraja datoteke prema početku datoteke.
Funkcija fseek() vraća vrijednost 0 ako je operacija uspješna, a ako je operacija neuspješna
vraća vrijednost različitu od nule.
Uočite:
fseek(fp,0, SEEK_SET)) je jednako rewind(fp).
Veličinu datoteke u bajtima se može dobiti naredbama:
fseek(fp, 0, SEEK_END);
size = ftell(fp);
Primjer: U programu seek.c generira se datoteka "random.dat" s 50 slučajnih cijelih brojeva.
Zatim se po proizvoljnom redoslijedu čita vrijednosti iz te datoteke. Redoslijed bira korisnik
tako da unosi indeks elementa. Program završava kada korisnik unese negativnu vrijednost.
/* Program fseek.c */
#include <stdlib.h>
#include <stdio.h>
#define MAX 50
int main()
{
FILE *fp;
int data, i, niz[MAX];
long pomak;
/* Inicijaliziraj niz od 50 elemenata po slucajnom uzorku */
for (i = 0; i < MAX; i++)
niz[i] = rand();
/* Otvori binarnu datoteku RANDOM.DAT za čitanje i pisanje. */
if ( (fp = fopen("RANDOM.DAT", "w+b")) == NULL)
{
fprintf(stderr, "nGreska pri otvaranje datoteke");
exit(1);
}
/* upiši niz */
if ( (fwrite(niz, sizeof(int), MAX, fp)) != MAX)
{
fprintf(stderr, "nGreska pisanja u datoteku");
exit(1);
207](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-207-320.jpg)

![vrijednost 0 ako je operacija uspješna, a ako je operacija neuspješna vraća vrijednost -1.
Razlog neuspješne operacije može biti:
• ne postoji datoteka ime
• već postoji datoteka s imenom novo_ime
• zadano je novo_ime s drugom oznakom diska
Privremene datoteke
Ponekad je potrebno formirati tzv. privremenu datoteku koja će poslužiti za smještaj podataka
koji se vrši samo za vrijeme izvršenja programa. Tada nije bitno kako se datoteka zove, jer se
nju treba izbrisati prije nego završi program. Za formiranje imena privremene datoteke može se
koristiti funkcija tmpname(), koja je deklarirana u <stdio.h>. Prototip joj je:
char *tmpnam(char *s);
Argument funkcije je pokazivač stringa koji pokazuje na memoriju koja je dovoljna za smještaj
imena datoteke. Ako je taj pokazivač jednak NULL tada funkcija tmpname() koristi vlastiti
statički spremnik u kojem generira neko ime. Funkcija tada vraća pokazivač na taj spremnik.
Način formiranja imena privremene datoteke je određen na način koji osigurava da se u jednom
programu ne mogu pojaviti dva ista imena za privremenu datoteku.
Primjer: u programu tmpname.c demonstrira se korištenje tzv. privremenih datoteka
/* Datoteka: tmpname.c
* Formiranje privremenih datoteka */
#include <stdio.h>
int main()
{
char ime[80];
FILE *tmp;
/* Formiraj privremenu datorteku */
tmpnam(ime);
tmp = fopen(ime, "w");
if(tmp != NULL)
{
/* koristi datoteku */
printf("Formirana datoteka imena: %sn", ime);
/* nakon koristenja zatvori datoteku **/
fclose(tmp);
/* i izbrisi je s diska */
remove(ime);
}
}
Dobije se ispis:
Formirana datoteka imena: s3a4.
209](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-209-320.jpg)






![Implementacija se može izvršiti na više načina. Sada će biti opisana implementacija u kojoj
se za spremanje elemenata stoga koristi podatkovna struktura tipa dinamičkog niza, a u
poglavlju 18 bit će pokazana implementacija pomoću strukture podataka tipa vezane liste.
Implementacija ADT STACK pomoću dinamičkog niza je opisana u datoteci "stack-arr.c".
/* Datoteka: stack-arr.c:
* Implementacija ADT STACK pomoću niza
*/
#include <stdlib.h>
#include "stack.h"
#define STACK_GROW 10U
#define STACK_SIZE 100U
/* typedef int stackElemT; definirano in stack.h*/
/* typedef struct stack *STACK; definirano in stack.h*/
struct stack {
stackElemT *A;
unsigned top; /* indeks poviše stvarnog vrha stoga*/
unsigned size; /* veličina niza*/
};
static void stack_error(char *s)
{
printf("nGreska: %sn", s); exit(1);
}
STACK stack_new(void)
{
STACK S = malloc(sizeof(struct stack));
if(S != NULL) {
S->size = STACK_SIZE;
S -> top = 0;
S->A = malloc(sizeof(stackElemT) * S->size);
if(S->A == NULL) {free(S); S=NULL;}
}
return S;
}
void stack_free(STACK S)
{
if(S->A != NULL) free(S->A);
if(S != NULL) free(S);
}
int stack_empty(STACK S) { return (S->top <= 0); }
stackElemT stack_pop(STACK S)
{
if(stack_empty(S)) stack_error("Stog prazan");
return S->A[--(S->top)];
}
void stack_push(STACK S, stackElemT x)
{
if (S->top >= S->size) {
S->size += STACK_GROW;
216](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-216-320.jpg)
![S->A = realloc(S->A, sizeof(stackElemT) * S->size);
if(S->A == NULL)
stack_error("Nema slobodne memorije");
}
S->A[(S->top)++] = x;
}
stackElemT stack_top(STACK S)
{
if(stack_empty(S)) stack_error("Stog prazan");
return S->A[S->top-1];
}
Testiranje ADT STACK provodi se programom stack-test.c.
/* Datoteka: stack-test.c */
#include <stdio.h>
#include <stdlib.h>
#include "stack-arr.c"
void upute(void) /* Upute za korisnika */
{
printf("Otipkaj:n"
"1 - push - gurni vrijednost na stogn"
"2 - pop - skini vrijednost sa stogan"
"0 - kraj programan");
}
int main(void)
{
int izbor, val;
STACK stog = stack_new();
upute(); printf("? ");
scanf("%d", &izbor);
while (izbor != 0) {
switch (izbor) {
case 1: /* push */
printf("Unesi integer: ");
scanf("%d", &val);
stack_push(stog, val);
break;
case 2: /* pop */
if (!stack_empty(stog))
printf("Podignuta je vrijednost %d.n",
stack_pop(stog));
else
printf("Stog je prazan.n");
break;
default:
printf("Pogresan odabir opcije. Ponovi!nn");
upute();
break;
}
printf("? ");
scanf("%d", &izbor);
}
217](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-217-320.jpg)


![/* Datoteka polish.c:
* Proracun izraza postfiksne notacije
*/
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <ctype.h>
#include "stack.h"
#include "stack-arr.c"
#define Pop() stack_pop(stack)
#define Top() stack_top(stack)
#define Push(x) stack_push(stack, (x))
main(int argc, char *argv[])
{
char *str;
int i, len, tmp;
STACK stack;
if (argc < 2) {
printf("Za proracun (30/(5-2))*10 otkucaj:n");
printf("c:> polish "30 5 2 - / 10 *"n");
exit(1);
}
str = argv[1];
len = strlen(str);
stack = stack_new();
for (i = 0; i < len; i++)
{
if (str[i] == '+') Push(Pop()+ Pop());
if (str[i] == '*') Push(Pop()* Pop());
if (str[i] == '-') { tmp = Pop(); Push(Pop()- tmp); }
if (str[i] == '/') {
int tmp = Pop();
if (tmp==0) {printf("Djeljenje s nulomn"); exit(1);}
Push(Pop() / tmp);
}
if (isdigit(str[i])) /* konverzija niza znamenki u broj */
{
Push(0);
do {
Push(10*Pop() + (int)str[i]-'0');
i++;
} while (isdigit(str[i]));
i--;
}
}
printf("Rezultat: %s = %d n", str, Pop( ));
stack_free(stack);
}
220](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-220-320.jpg)

![Početno je red prazan - - - - - -
Front=back (red prazan)
Front = back;
Nakon operacija put() povećava put('a'); put('b')
se indeks back za 1 a b - - - -
front back
Operacija get() dobavlja element x = get() /* x sadrži vrijednost a */
kojem je indeks jednak front, a a b - - - -
zatim se front povećava za front back
jedan.
Što napraviti kada, nakon put('c'); put('d'); put('e');
višestrukog unosa, back postane - b c d E -
jednak krajnjem indeksu niza? front back
Ideja je da se back ponovo put('f')
postavi na početak niza (takovi - b C d e f
spremnik se nazivaju cirkularni back front (red popunjen)
spremnik). Time se maksimalno
iskorištava prostor spremnika za Red popunjen ako je:
smještaj elemenata reda. (back+1) % QUEUEARRAYSIZE == front
U datoteci "queue_arr.c" realiziran je ADT QUEUE pomoću cirkularnog spremnika.
/* Datoteka: queue-arr.c
* QUEUE realiziran kao cirkularni spremnik
*/
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include "queue.h"
#define QUEUESIZE 100 /* maksimalni broj elemenata */
#define QUEUEARRAYSIZE (QUEUESIZE +1) /* veličina niza */
/* typedef int queueElemT; */
/* typedef struct queue *QUEUE; definirani u queue.h*/
struct queue {
queueElemT A[QUEUEARRAYSIZE];
int front;
int back;
};
QUEUE queue_new(void)
{
QUEUE Q = malloc(sizeof(struct queue));
if(Q != NULL) Q->front = Q->back = 0;
return Q;
}
void queue_free(QUEUE Q)
{
assert(Q != NULL);
if(Q != NULL) free(Q);
222](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-222-320.jpg)
![}
int queue_empty(QUEUE Q)
{
assert(Q != NULL);
return (Q->front == Q->back);
}
int queue_full(QUEUE Q)
{
assert(Q != NULL);
return ((Q->back + 1) % QUEUEARRAYSIZE == Q->front);
}
void queue_put(QUEUE Q, queueElemT x)
{
assert(Q != NULL);
Q->A[Q->back] = x;
Q->back = (Q->back + 1) % QUEUEARRAYSIZE;
}
queueElemT queue_get(QUEUE Q)
{
queueElemT x;
assert(Q != NULL);
x = Q->A[Q->front];
Q->front = (Q->front +1) % QUEUEARRAYSIZE;
return x;
}
void queue_print(QUEUE Q)
{
int i;
assert(Q != NULL);
printf("Red: ");
for(i = Q->front % QUEUEARRAYSIZE; i < Q->back;
i=(i+1)% QUEUEARRAYSIZE )
printf("%d, ", Q->A[i]);
printf("n");
}
Testiranje ADT QUEUE provodi se programom queue-test.c.
/* Datoteka: queue-test.c */
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include "queue.h"
#include "queue-arr.c"
void upute(void)
{ printf ("Izbornik:n"
" 1 Umetni broj u Redn"
" 2 Odstrani broj iz Redan"
" 0 Krajn");
}
int main()
223](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-223-320.jpg)






![C -> B
A -> B
U ovom primjeru je očito da se pomoću rekurzije dobije fascinantno jednostavno rješenje
problema. Teško da postoji neka druga metoda kojom bi se ovaj problem mogao riješiti na
jednako efikasan način.
Zadatak: Provjerite izvršenje programa za slučaj da broj diskova iznosi: 2, 3, 4 i 5. Pokazat će
se da broj operacija iznosi 2n-1, što se može i logično zaključiti, jer se povećanjem broja
diskova za jedan udvostručuje broj rekurzivnih poziva funkcije pomakni_kulu(), a u
temeljnom slučaju se vrši samo jedna operacija.
Procijenite koliko bi trajalo izvršenje programa pod uvjetom da izvršenje jedne operacije traje
1us i da se koristi 64 diska. Da li izvršenje tog program traje dulje od životog vijeka čovjeka?
17.4 Metoda - podijeli pa vladaj (Divide and Conquer)
U analizi programskih metoda često se spominje metoda "podijeli pa vladaj". Kod nje se
rekurzija nameće kao prirodni način rješenja problema. Opći princip metode je da se problem
logično podijeli u više manjih problema, tako da se rješenje dalje može odrediti rješavanjem
jednog od tih "manjih" problema.
17.4.1 Drugi korijen broja
Metodu podijeli pa vladaj primijenit ćemo za približan proračun drugog korijena broja n.
Metoda: Numerički se proračuni mogu provesti samo s ograničenom točnošću. Zbog toga
zadovoljava postupak u kojem se određuje da vrijednost x predstavlja drugi korijen od n, ako je
razlika (n – x2) približno jednaka nuli, odnosno manja od po volji odabrane vrijednosti epsilon.
Točno rješenje se nalazi unutar nekog intervala [d,g]. Primjerice, sigurno je da se rješenje nalazi
u intervalu [0,n] ako je n>1, odnosno u intervalu [0,1] ako je n<1. Interval može biti i uži ako
smo sigurni da obuhvaća točno rješenje.
Do rješenja se dolazi rekurzivno:
Temeljni slučaj:
Ukoliko se uzme da je vrijednost od x u sredini intervala [d,g], tj. x=(d+g)/2, može se
prihvatiti da je to zadovoljavajuće rješenje, ako je širina intervala manja od neke po
volji odabrane vrijednosti epsilon (pr. 0,000001) , tj. ako je je g-d < epsilon.
Ako je širina intervala veća od epsilon, do rješenje se dolazi koristeći rekurziju
prema pravilu (2).
Pravilo rekurzije:
Ako je n < x2 rješenje se traži u intervalu [d, x],
inače, rješenje se traži u intervalu [x, g].
Implementacija: U programu korijen.c implementirana je i testrirana funkcija
DrugiKorijen(n), koja vraća drugi korijen od n. U toj funkciji se prvo određuje donja i
gornja granica intervala unutar kojega se nalazi rješenje, a zatim se poziva funkcija
korijen_rek(n, d, g) koja obavlja proračun prema prethodnom rekurzivnom algoritmu.
Točnost proračuna se ispituje usporedbom s vrijednošću kojeg vraća standardna funkcija
sqrt(n).
230](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-230-320.jpg)
![/* Program korijen.c */
#include <stdio.h>
#include <math.h>
#define EPSILON 0.000001 /* proizvoljni kriterij točnosti */
double korijen_rek(double n, double d, double g)
{
double x = (d + g)/ 2.0;
if (g - d < EPSILON) /* temeljni slučaj */
return x;
else if (n < x*x ) /* pravilo rekurzije */
return korijen_rek (n, d, x);
else
return korijen_rek (n, x, g);
}
double DrugiKorijen(double n)
{
double g, d=0.0;
/* početne granice d=0.0, g=n ili 1 ako je n<1*/
if(n < 0) n= -n; /* samo za pozitivne vrijednosti */
if(n>1) g=n;
else g=1.0;
return korijen_rek(n, d, g);
}
int main( int argc, char *argv[])
{
int i;
double n;
for (i = 1; i < argc; i++)
{
sscanf( argv[i], "%lf", &n);
printf("Drugi korijen(%f) = %f (treba biti %f)n",
n, DrugiKorijen(n), sqrt(n));
}
return 0;
}
Nakon poziva programa:
c:>korijen 5 7.6 3.14
Dobije se ispis:
Drugi korijen (5.000000) = 2.236068 (treba biti 2.236068)
Drugi korijen (7.600000) = 2.756810 (treba biti 2.756810)
Drugi korijen (3.140000) = 1.772004 (treba biti 1.772005)
17.4.2 Binarno pretraživanje niza
Drugi primjer primjene metode podijeli pa vladaj je traženje elementa sortiranog niza
metodom koja se naziva binarno pretraživanje niza.
Zadatak: Zadan je niz cijelih brojeva a[n] kojem su elementi sortirani od manje prema većoj
vrijednosti, tj.
a[i-1] < a[i], za i=1,..n-1
231](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-231-320.jpg)
![Potrebno je odrediti da li se u ovom nizu nalazi element vrijednosti x, i to pomoću funkcije
int binSearch( int a[],int x, int d, int g);
koja vraća indeks elementa a[i], kojem je vrijednost jednaka traženoj vrijednosti x. Ako
vrijednost od x nije jednaka ni jednom elementu niza, funkcija binSearch() vraća negativnu
vrijednost -1. Cjelobrojne vrijednosti d i g predstavljaju indekse niza koji određuju interval
[d,g] unutar kojeg se vrši traženje.
Metoda: Problem se može riješiti rekurzivno na sljedeći način: Ako u nizu a[i] postoji element
jednak traženoj vrijednosti x, njegov indeks je iz intervala [d,g], gdje mora biti istinito g >= d.
Trivijalni slučaj je za d=0, g=n-1, koji obuhvaća cijeli niz.
Temeljni slučaj:
Razmatra se element niza indeksa i = (g+d)/2 (dijelimo niz na dva podniza).
Ako je a[i] jednak x, pronađen je traženi element niza, a funkcija vraća indeks i.
Pravilo rekurzije:
Ako je a[i] <x rješenje se traži u intervalu [i+1, g], inače je u intervalu [d, i-1].
Implementacija:
int binSearch( int a[],int x, int d, int g)
{
int i;
if (d > g) return –1;
i = (d + g)/ 2;
if (a[i] == x) return i;
if (a[i] < x) return binSearch( a, x, i + 1, g);
else return binSearch( a, x, d, i - 1);
}
Proces traženja vrijednosti x=23 u nizu od 14 elemenata, ilustriran je na slici 17.3.
0 1 2 3 4 5 6 7 8 9 10 11 12 13
1 2 3 5 6 8 9 12 23 26 27 31 34 42
D i g
1 2 3 5 6 8 9 12 23 26 27 31 34 42
d i g
1 2 3 5 6 8 9 12 23 26 27 31 34 42
d i g
1.korak: d=0, g=13, i=6, a[6]<23
2.korak: d=i+1=7,g=14, i=10, a[10]>23
3.korak: d=7, g=i-1=9, i=8, a[8]==23
Slika 17.3. Binarno pretraživanje niza
17.5 Pretvorba rekurzije u iteraciju
Neke rekurzivne funkcije se mogu transformirati u funkcije koje umjesto rekurzije koriste
iteraciju. To su funkcije u kojima je rekurzivni poziv funkcije posljednja naredba u tijelu
funkcije, primjerice
232](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-232-320.jpg)
![void petlja()
{
iskaz ...
if (e) petlja();
}
U ovom slučaju, rekurzivni poziv funkcije petlja(), znači da se izvršenje vraća na početak
tijela funkcije, zbog toga se ekvivalentna verzija funkcije može napisati tako da se umjesto
poziva funkcije koristi goto naredba s odredištem na prvu naredbu tijela funkcije, tj.
void petlja()
{
start: iskaz ...
if (e) goto start;
}
Rekurzivni poziv, koji se vrši na kraju (ili na repu) tijela funkcije, često se naziva "repna
rekurzija". (eng. tail recursion). Neki optimizirajući kompilatori mogu prepoznati ovakav oblik
rekurzivne funkcije i transformirati rekurzivno tijelo funkcije u iterativnu petlju. Na taj način
se dobije efikasnija funkcija, jer se ne gubi vrijeme i prostor na izvršnom stogu koji su potrebni
za poziv funkcije.
Kod većine se rekurzivnih funkcija ne može izvršiti ova transformacije. Primjerice,
funkcija fact() nije repno rekurzivna jer se u posljednjoj naredbi (return fact(n-1)*n;)
najprije vrši poziv funkcije fact(), a zatim naredba množenja. Funkcija binSearch(), koja
je opisana u prethodnom odjeljku, može se transformirati u funkciju s repnom rekurzijom, na
sljedeći način:
int binSearch( int a[],int x, int d, int g)
{
int i;
if (d > g) return –1;
i = (d + g)/ 2;
if (a[i] == x) return i;
if (a[i] < x) d=i+1;
else g=i-1
return binSearch( a, x, d, g);
}
Dalje se može provesti transformacija u iterativnu funkciju
int binSearch( int a[],int x, int d, int g)
{
int i;
start: if (d > g) return –1;
i = (d + g)/ 2;
if (a[i] == x) return i;
if (a[i] < x) d=i+1;
else g=i-1
goto start;
}
Može se napisati iterativno tijelo funkcije i u obliku while petlje:
int binSearch( int a[],int x, int d, int g)
{
int i;
while (d <= g) {
233](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-233-320.jpg)
![i = (d + g)/2;
if (a[i] == x) return i;
if (a[i] < x) d=i+1;
else g=i-1;
}
return –1;
}
Iterativna verzija se može pojednostaviti u slučaju kada se pretražuje cijeli niz. Tada kao
argument funkcije nije potrebna donja granica indeksa, jer je ona jednaka nuli, a umjesto gornje
granice indeksa, argument je broj elemenata niza n.
int binSearch( int a[],int x, int n)
{
int i, d=0, g=n-1;
while (d <= g) {
i = (d + g)/2;
if (a[i] == x) return i;
if (a[i] < x) d=i+1;
else g=i-1;
}
return –1;
}
17.6 Standardna bsearch() funkcija
U standardnoj biblioteci implementirana je polimorfna funkcija bsearch(). Služi za binarno
pretraživanje nizova s proizvoljnim tipom elemenata niza. Deklarirana je na sljedeći način:
void *bsearch( const void *px, const void *niz,
size_t n, size_t el_size,
int (*pCmpFun)(const void *, const void *) );
Prvi parametar funkcije je pokazivač na objekt kojeg se traži. Drugi parametar je pokazivač na
prvi element niza od n elemenata koji zauzimaju el_size bajta. Posljednji parametar je
pokazivač na usporednu funkciju koja je ista kao kod qsort() funkcije. Funkcija bsearch()
vraća pokazivač na element niza ili NULL ako niz ne sadrži traženi objekt.
Realizacija te funkcije, ali pod imenom binsearch(), dana je i testirana programom
binsearch.c, i to za slučaj da se vrši pretraživanje niza stringova.
/* Datoteka: binsearch.c */
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef char *string;
void * binsearch( const void *px, const void *niz,
size_t n, size_t el_size,
int (*pCmpFun)(const void *, const void *) )
{
int i, cmp, d=0, g=n-1;
char * adr;
234](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-234-320.jpg)
![while (d <= g)
{
i = (d + g)/2;
/* adresa i-tog elementa niza*/
adr = (char *)niz + i*el_size;
/*el. niza na toj adresi usporedi s objektom *px */
cmp = (*pCmpFun)((void *)adr, (void *)px);
if (cmp == 0) return (void *) adr; /* objekt pronađen */
if (cmp < 0) d=i+1;
else g=i-1;
}
return NULL;
}
int UsporediStringove( const void *pstr1, const void *pstr2 )
{
/* Argumenti funkcije su pokazivači na objekte koje
* usporedjujemo, u ovom slučaju objekt je string (char *).
* Funkcija strcmp() prima argumente tipa string, stoga
* treba izvršiti pretvorbu tipa i indirekciju da bi dobili
* string,kao argument za strcmp()
* ( str = *(string *) pstr))
*/
return strcmp( *(string*) pstr1, *(string*)pstr2 );
}
int main( void )
{
string txt[] = {"Ante", "Ivo", "Marko", "Jure", "Bozo"};
int numstrings = sizeof(txt)/sizeof(txt[0]);
string key="Ivo";
int i, idx;
string * rez;
/* sortiraj niz stringova leksikografski */
qsort((void *)txt, numstrings, sizeof(char*),
UsporediStringove);
for(i = 0; i < numstrings; i++ ) puts(txt[i]) ;
/* pronađi string key */
rez =(string*) binsearch(&key, txt,
numstrings, sizeof(char*),
UsporediStringove);
if(rez != NULL)
printf("Pronadjen string "%s" na adresi %Fpn",
*pstr, pstr);
else
printf("Nije pronadjen string "%s" n", key);
return 0 ;
}
235](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-235-320.jpg)
![Dobije se ispis:
Ante Ivo Marko Jure Bozo
Nakon sortiranja:
Ante Bozo Ivo Jure Marko
Pronadjen string "Ivo" na adresi 0022FF48
17.7 Složenost algoritama - "Veliki - O" notacija
Pri analizi složenosti algoritama uvodi se mjera "dimenzije problema". Primjerice, kada se
obrađuju nizovi, onda dimenziju problema predstavlja duljina niza n, a kada su u pitanju
kvadratne matrice, onda je dimenzija matrice istovremeno i dimenzija problema. Ako je n
dimenzija problema, onda se efikasnost korištenja memorije može opisati funkcijom M(n), a
vrijeme izvršenja algoritma funkcijom T(n).
Funkcija T(n) se često naziva vremenska složenost algoritma (engl. time complexity), dok
je M(n) prostorna složenost. Funkciji T(n) se pridaje znatno više značaja nego veličini M(n), pa
se pod skraćenim pojmom "složenost" (eng. complexity) obično podrazumijeva vremenska
složenost. Razlog tome je iskustvo u razvoju algoritama, koje je pokazalo da je zauzeće
memorije znatno manji problem od postizanja prihvatljivog vremena obrade.
Analiza brzine izvršenja programa se radi tako da se odredi ukupan broj operacija koje
dominantno troše procesorsko vrijeme. Primjerice, u programu za zbrajanje elemenata
kvadratne matrice, dimenzija nxn, označen je broj ponavljanja naredbi u kojima se vrši
zbrajanje.
NAREDBE PROGRAMA BROJ PONAVLJANJA
S = 0 ; .
for(i=0; i<n; i++) n
for(j=0; j<n; j++) n*n
S = S + M[i][j] n*n
Ako se uzme da prosječno vrijeme izvršenja jedne naredbe iznosi t0, dobije se da ukupno
vrijeme izvršenja algoritma iznosi:
T(n) = (2n² + n)*t0
Veličina T(n) je posebno važna za velike vrijednosti od n. U tom slučaju je:
T(n) ≤ konst * n²
Ovaj se zaključak u računarskoj znanosti piše u obliku tzv. "veliki-O" notacije:
T(n) = O(n²)
i kaže se da je T(n) "veliki O od n²". Funkcija f(n) = n² predstavlja red složenosti algoritma.
Uočite da vrijednost konstantnog faktora ne određuje složenost algoritma već samo faktor koji
ovisi o veličini problema.
Definicija: Složenost algoritma u "veliki-O" notaciji definira se na sljedeći način:
T(n) = O( f(n) ), (čita se: T je veliki-O od f)
236](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-236-320.jpg)

![Linearni algoritmi
Linearni algoritmi se javljaju u svim slučajevima gdje je obradom obuhvaćeno n istovjetnih
podataka i gdje udvostručenje količine radnji ima za posljedicu udvostručenje vremena obrade.
Opći oblik linearnog algoritma može se prikazati u vidu jedne for petlje:
for (i=0; i < n; i++)
{obrada koja traje vrijeme t}
Zanemarujući vrijeme opsluživanja for petlje, u ovom slučaju funkcija složenosti je T(n)=nt,
pa je T(n) = O(n).
U slučajevima kada nije moguće deterministički odrediti vrijeme izvršavanja sadržaja petlje
može se umjesto vremena rada T(n) statistički odrediti srednji broj naredbi I(n) koje program
obavlja. Tada se podrazumijeva da je T(n)=t1*I(n), gdje je vrijeme izvršavanja prosječne
naredbe t1 = konst.
Budući da vrijedi
T(n) = O( f(n) ) , I(n) = O( f(n) ),
slijedi da se traženi red funkcije složenosti f(n) može odrediti kako iz T(n), tako i iz I(n).
Primjerice, pronalaženje maksimalne vrijednosti elementa niza ima sljedeću analizu broja
naredbi:
NAREDBE PROGRAMA BROJ PONAVLJANJA
max = a[0] 1
for(i=1; i<n; i++) (n-1)
if (a[i] > max) (n-1)
max = a[i] (n-1)p (0<=p<=1)
Ovdje p označava vjerojatnost da dođe do ispunjenja uvjeta a[i]>max ( p ne ovisi od n).
Sumirajući broj ponavljanja pojedinih naredbi dobije se da je ukupan broj izvršenih naredbi
I(n) = 1 + (n-1)(3+p) = (3+ p) n - 1 - p.
U ovom je izrazu dominantan samo prvi član polinoma, pa je f(n) = n, odnosno T(n) = O(n).
Linearno-logaritamski algoritmi
Linearno-logaritamski algoritmi, složenosti O(n log n) ), spadaju u klasu veoma efikasnih
algoritama jer im složenost, za veliki n, raste sporije od kvadratne funkcije. Primjer za ovakav
algoritam je Quicksort, koji će biti detaljno opisan kasnije. Bitna osobina ovih algoritama je
sljedeća:
(1) Obaviti pojedinačnu obradu kojom se veličina problema prepolovi.
(2) Unutar svake polovine sekvencijalno obraditi sve postojeće podatke.
(3) Nastaviti razlaganje problema dok se ne dođe do veličine 1.
Slično kao i kod logaritamskih algoritama i ovdje je ukupan broj dijeljenja log2n, ali kako
se nakon svakog dijeljenja sekvencijalno obrade svi podaci, to je ukupan broj elementarnih
obrada jednak nlog2n, i to predstavlja red funkcije složenosti.
238](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-238-320.jpg)
![Kvadratni i stupanjski algoritmi
Kvadratni algoritmi, složenosti O(n2), najčešće se dobivaju kada se koriste dvije for petlje
jedna unutar druge. Primjer je dat na početku ovog poglavlja. Stupanjski algoritmi nastaju kod
algoritama koji imaju k umetnutih petlji, pa je složenost O(nk).
Eksponencijalni algoritmi
Eksponencijalni algoritmi O(kn) spadaju u kategoriju problema za koje se suvremena
računala ne mogu koristiti, izuzev u slučajevima kada su dimenzije takvog problema veoma
male. Jedan od takovih primjera je algoritam koji rekurzivno rješava igru "Kule Hanoja",
opisan u prethodnom poglavlju.
Faktorijelni algoritmi
Kao primjer faktorijelnih algoritama najčešće se uzima problem trgovačkog putnika.
Problem je formuliran na sljedeći način: zadano je n+1 točaka u prostoru i poznata je udaljenost
između svake dvije točke j i k. Polazeći od jedne točke potrebno je formirati putanju kojom se
obilaze sve točke i vraća u polaznu točku, tako da je ukupni prijeđeni put minimalan.
Trivijalni algoritam za rješavanje ovog problema mogao bi se temeljiti na uspoređivanju
duljina svih mogućih putanja. Broj mogućih putanja iznosi n!. Polazeći iz početne točke postoji
n putanja do n preostalih točaka. Kada odaberemo jednu od njih i dođemo u prvu točku onda
preostaje n-1 mogućih putanja do druge točke, n-2 putanja do treće točke, itd., n+1-k putanja do
k-te točke, i na kraju samo jedna putanja do n-te točke i natrag u polaznu točku. Naravno da
postoje efikasnije varijante algoritma za rješavanje navedenog problema, ali u opisanom slučaju,
s jednostavnim nabrajanjem i uspoređivanjem duljina n! različitih zatvorenih putanja, algoritam
ima složenost O(n!).
17.8 Sortiranje
Sortiranje je postupak kojim se neka kolekcija elemenata uređuje tako da se elementi
poredaju po nekom kriteriju. Kod numeričkih nizova red elemenata se obično uređuje od
manjeg prema većim elementima. Kod nizova stringova red se određuje prema leksikografskom
rasporedu. Kod kolekcija strukturnog tipa obično se odabire jedan član strukture kao ključni
element sortiranja. Sortiranje je važno u analizi algoritama, jer su analizom različitih metoda
sortiranja postavljeni neki od temeljnih kompjuterskih algoritama.
Za analizu metoda sortiranja postavlja se sljedeći problem: odredite algoritam pomoću
kojeg se ulazni niz A[0..n-1], od n elemenata, transformira u niz kojem su elementi poredani u
redu od manjeg prema većem elementu, tj. na izlazu treba biti ispunjeno:
A[0] ≤ A[1] ≤ A[2] ≤ ... ≤ A[n-2] ≤ A[n-1].
Najprije će biti analizirane dvije jednostavne metode, selekcijsko sortiranje i sortiranje
umetanjem, kojima je složenost O(n2). Zatim će biti analizirane dvije napredne metode,
quicksort i mergesort, koje koriste metodu "podijeli pa vladaj". Njihova je složenost O(n log2
n). U analizi će biti korištena oznaka A[d..g] za označavanje da se analizira neki niz od indeksa
d do indeksa g. Ovaj način označavanja ne vrijedi u C jeziku.
17.8.1 Selekcijsko sortiranje
Ideja algoritma je:
1. Pronađi najmanji element i njegov indeks k.
2. Taj element postavi na početno mjesto u nizu (A[0]), a element koji je dotad postojao
na indeksu 0 postavi na indeks k.
239](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-239-320.jpg)
![3. Zatim pronađi najmanji element, počevši od indeksa 1. Kada ga pronađeš, zamijeni ga
s elementom indeksa 1.
4. Ponovi postupak (3) za sve indekse (2..n-2).
Primjerice za sortirati niz od 6 elemenata: 6, 4, 1, 5, 3 i 2 , treba izvršiti sljedeće operacije:
6 4 1 5 3 2 -> min od A[0..5] zamijeni sa A[0]
1 4 6 5 3 2 -> min od A[1..5] zamijeni sa A[1]
1 2 6 5 3 4 -> min od A[2..5] zamijeni sa A[2]
1 2 3 5 6 4 -> min od A[3..5] zamijeni sa A[3]
1 2 3 4 6 5 -> min od A[4..5] zamijeni sa A[4]
1 2 3 4 5 6 -> niz je sortiran
Ovaj algoritam se može implementirati pomoću for petlje:
for (i = 0; i < n-1; i++)
{
imin = indeks najmanjeg elementa u A[i..n-1];
Zamijeni A[i] sa A[imin];
}
Uočite da se petlja izvršava dok je i < n-1, a ne za i < n, jer ako A[0..n-2] sadrži n-1 najmanjih
elemenata, tada posljednji element mora biti najveći, i on se nalazi na ispravnom položaju , tj.
A[n-1].
Indeks najmanjeg elementa u A[i..n-1] pronalazi se sa:
imin = i;
for (j = i+1; j < n; j++)
if (A[j] < A[min]) imin=j;
Zamjenu vrijednosti vrši funkcijom swap();
/* Zamjena vrijednosti dva int */
void swap(int *a, int *b)
{
int t = *a;
*a = *b;
*b = t;
}
Sada se može napisati funkcija za selekcijsko sortiranje, niza A koji ima n elemenata, u obliku:
void selectionSort(int *A, int n)
{
int i, j, imin; /* indeks najmanjeg elementa u A[i..n-1] */
for (i = 0; i < n-1; i++) {
/* Odredi najmanji element u A[i..n-1]. */
imin = i; /* pretpostavi da je to A[i] */
for (j = i+1; j < n; j++)
if (A[j] < A[imin]) /* ako je A[j] najmanji */
imin = j; /* zapamti njegov indeks */
/* Sada je A[imin] najmanji element od A[i..n-1], */
/* njega zamjenjujemo sa A[i]. */
240](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-240-320.jpg)
![swap(&A[i], &A[imin]);
}
}
Analiza selekcijskog sortiranja
Svaka iteracija vanjske petlje (indeks i) traje konstantno vrijeme t1 plus vrijeme izvršenja
unutarnje petlje (indeks j). Svaka iteracija u unutarnjoj petlji traje konstantno vrijeme t2 .
Broj iteracija unutarnje petlje ovisi u kojoj se iteraciji nalazi vanjska petlja:
Broj operacija u
i
unutarnjoj petlji
0 n-1
1 n-2
2 n-3
... ...
n-2 1
Ukupno vrijeme je:
T(n) = [t1 + (n-1) t2] + [t1 + (n-2) t2] + [t1 + (n-3) t2] + ... + [t1 + (1) t2]
odnosno, grupirajući članove u oblik t1 ( …) + (...) t2 dobije se
T(n) = (n-1) t1 + [ (n-1) + (n-2) + (n-3) + ... + 1 ] t2
Izraz u uglatim zagradama predstavlja sumu aritmetičkog niza
1 + 2 + 3 + ... + (n-1) = (n-1)n/2 = (n2-n)/2,
pa je ukupno vrijeme jednako:
T(n) = (n-1) t1 + [(n2-n)/2] t2 = - t1 + t1 n - t2 n/2 + t2 n2/2
Očito je da dominira član sa n2 , pa je složenost selekcijskog sortiranja jednaka O(n2) .
17.8.2 Sortiranje umetanjem
Algoritam sortiranja umetanjem (eng. insertion sort) se temelji na postupku koji je sličan načinu
kako se slažu igraće karte. Algoritam se vrši u u n-1 korak. U svakom koraku se umeće i-ti
element u dio niza koji mu prethodi (A[0..i-1]), tako taj niz bude sortiran. Primjerice, sortiranje
niza od n=6 brojeva izgleda ovako:
6 4 1 5 3 2 -> ako je A[1]< A[0], umetni A[1] u A[0..0]
4 6 1 5 3 2 -> ako je A[2]< A[1], umetni A[2] u A[0..1]
1 4 6 5 3 2 -> ako je A[3]< A[2], umetni A[3] u A[0..2]
1 4 5 6 3 2 -> ako je A[4]< A[3], umetni A[4] u A[0..3]
1 3 4 5 6 2 -> ako je A[5]< A[4], umetni A[5] u A[0..4]
1 2 3 4 5 6 -> niz je sortiran
Algoritam se može zapisati pseudokôdom:
for (i = 1; i < n; i++)
{
241](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-241-320.jpg)
![x = A[i];
analiziraj elemente A[0 .. i-1]
počevši od indeksa j=i-1, do indeka j=0
ako je x < A[j] tada
pomakni element A[j] na mjesto A[j+1]
inače prekini
zatim umetni x na mjesto A[j+1]
}
pa se dobije funkcija:
void insertionSort(int *A, int n)
{
int i, j, x;
for (i = 1; i < n; i++) {
x = A[i];
for(j = i-1; j >= 0; j--) {
if(x < A[j])
A[j+1] = A[j];
else
break;
}
A[j+1] = x;
}
}
Analiza složenosti metode sortiranja umetanjem
Sortiranje umetanjem je primjer algoritma u kojem prosječno vrijeme izvršenja nije puno kraće
od vremena izvršenja koje se postiže u najgorem slučaju.
Najgori slučaj
Vanjska petlja se izvršava u n-1 iteracija, što daje O(n) iteracija. U unutarnjoj petlji se vrši od
0 do i<n iteracija, u najgorem slučaju vrši se također O(n) iteracija. To znači da se u najgorem
slučaju vrši O(n) ⋅O(n) operacija, dakle složenost je O(n2).
Najbolji slučaj
U najboljem slučaju u unutarnjoj petlji se vrši 0 iteracija. To nastupa kada je niz sortiran. Tada
je složenost O(n). Može se uzeti da to vrijedi i kada je niz "većim dijelom sortiran" jer se tada
rijetko izvršava unutarnja petlja.
Prosječni slučaj
U prosječnom se slučaju vrši n/2 iteracija u unutarnjoj petlji. To također daje složenost
unutarnje petlje O(n), pa je ukupna složenost: O(n2).
17.8.3 Sortiranje spajanjem sortiranih podnizova (merge sort)
Sortiranje metodom spajanja sortiranih podnizova (eng. merge sort) temelji se na ideji da se niz
rekurzivno dijeli na dva sortirana niza, te da se zatim izvrši spajanje tih sortiranih nizova.
Problem će biti riješen za slučaj da se sortira niz A[d..g], tj. od donjeg indeksa d do gornjeg
indeksa g, funkcijom
void mergeSort(int *A, int d, int g);
242](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-242-320.jpg)
![Rekurzivnom se podjelom niza u dva podniza, A[d..s] i A[s+1,g], koji su otprilike podjednake
veličine (indeks s se odredi kao srednja vrijednost s = (d+g)/2), dolazi se do temeljnog slučaja
kada u svakom nizu ima samo jedan element. Taj jedno-elementni niz je već sortiran, pa se pri
"izvlačenju" iz rekurzije može vršiti spajanje sortiranih podnizova. Ovaj postupak je ilustriran
na slici 4.
Slika 17. 4. Prikaz sortiranja spajanjem sortiranih podnizova
Za implementaciju ovog algoritma bitno je uočiti sljedeće:
• Ulazni niz nije nužno "fizikalno" dijeliti na podnizove, jer se podnizovi ne preklapaju.
Dovoljno je zapamtiti indekse ulaznog niza koji određuju neki podniz.
• Spajanje podnizova se uvijek provodi s elementima koji su u ulaznom nizu poredani
jedan do drugog; prvi podniz je A[d..s], a drugi podniz je A[s+1..g]. U tu svrhu koristit
će se funkcija:
void merge(int *A, int d, int s, int g)
/* Ulaz: dva sortirana niza A[d..s] i A[s+1..g] */
/* Izlaz: sortirani niz A[d..g] */
Očito je da se radi o algoritmu tipa "podijeli pa vladaj":
1. Podijeli: podijeli niz A[d,g], na način da dva podniza A[d,s] i A[s+1,g] sadrže otprilike
pojednak broj elemenata. To se postiže izborom: s=(d+g)/2.
2. Vladaj: rekurzivno nastavi dijeliti oba podniza sve dok njihova veličina ne postane
manja od 2 elementa (niz koji sadrži nula ili jedan element je sortirani niz).
3. Spoji: Nakon toga, pri "izvlačenju" iz rekurzije, izvrši spajanje sortiranih nizova
koristeći funkciju merge(A,d,s,g).
Implementacija ovog algoritma je jednostavna;
void mergeSort(int *A, int d, int g)
{
if (d < r ) { /* temeljni slucaj - 1 element */
int s = (d + g) / 2; /* s je indeks podjele niza */
mergeSort(A, d, s); /* rekurzivno podijeli A[d..s] */
mergeSort(A, s+1, g); /* rekurzivno podijeli A[s+1..g]*/
merge(A, d, s, g); /* zatim spoji sortirane nizove */
243](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-243-320.jpg)
![}
}
Još treba definirati funkciju merge(). Ona se može realizirati na način da se formiraju dva
pomoćna niza, donji[] i gornji[], u koje se kopira sortirane nizove A[d..s] i A[s+1..g].
Zatim se iz tih pomoćnih sortiranih nizova formira jedan sortirani niz u području ulaznog niza
A[d..g]. Postupak je ilustriran na slici 5.
Slika 17.5. Spajanje sortiranih nizova
Implementacija je sljedeća:
/* Spajanje podnizove A[d..s] i A[s+1..g] u sortirani niz A[d..g]. */
void merge(int *A, int d, int s, int g)
{
int m = s - d + 1; /* broj elemenata u A[d..s] */
int n = g - s; /* broj elemenata u A[s+1..g] */
int i; /* indeks u donji niz*/
int j; /* indeks u gornji niz*/
int k; /* indeks u orig. niz A */
int *donji = malloc(sizeof(int) * m); /* niz A[d..s] */
int *gornji = malloc(sizeof(int) * n); /* niz A[s+1..g] */
/* Kopiraj A[d..s] u donji[0..m-1] i A[s+1..g] u gornji[0..n-1]. */
for (i = 0, k = d; i < m; i++, k++)
donji[i] = A[k];
for (j = 0, k = s+1; j < n; j++, k++)
gornji[j] = A[k];
/* Usporedbom donji[0..m-1] i gornji[0..n-1], */
/* pomakni manji element na sljedeću poziciju u A[d..g]. */
i = 0; j = 0; k = d;
while(i < m && j < n; )
if (donji[i] < gornji[j])
A[k++] = donji[i++];
else
A[k++] = gornji[j++];
/* Preostale elemente jednostavno kopiraj */
/* Jedna od ove dvije petlje će imati nula iteracija! */
while (i < m)
A[k++] = donji[i++];
while (j < n)
A[k++] = gornji[j++];
244](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-244-320.jpg)
![/* Dealociraj memoriju koju zauzimaju donji i gornji. */
free(donji);
free(gornji);
}
Operacija kopiranja iz pomoćnih nizova u sortirani niz A[d..g] provodi se jednostavnom
usporedbom sadržaja donji[i] i gornji[j]. Kopira se manji element u A i inkrementira pozicija u
nizu. Na taj način, ova se operacija vrši u linearnom vremenu O(g-d+1).
Pomoćni nizovi su formirani alociranjem memorije, stoga se na kraju funkcije vrši oslobađanje
memorije. U realnoj se primjeni može koristiti brži postupak, bez alociranja memorije, na način
da se pomoćni nizovi deklariraju kao globalne varijable. Dimenzija ovih globalnih nizova mora
biti veća od polovine dimenzije niza koji se sortira. Na sličan način se može provesti i sortiranje
datoteka.
Složenost metode spajanja podnizova
Može se na jednostavan način pokazati da je vremenska složenost ovog algoritma jednaka O(n
log2 n), ukoliko se uzme da je veličina niza potencija broja 2, tj. da je n = 2m. Pošto se pri
svakom rekurzivnom pozivu niz dijeli na dva podniza, sve dok duljina podniza ne postane
jednaka 1, proizlazi da je broj razina podijele niza jednak log2 n. Na k-toj razini niz je podijeljen
na 2k podnizova duljine n/2k. To znači da spajanje sortiranih nizova na k-toj razini ima složenost
2kxO(n/2k)= O(n), a pošto ima log2 n razina, proizlazi da je ukupna složenost jednaka O(n log2
n). Do istog rezultata se dolazi i uz znatno rigorozniju analizu složenosti.
Može se pokazati da je ovo najbolji rezultat koji se može postići pri sortiranju nizova. Jedini
problem ovog algoritma je što zahtijeva povećanu prostornu složenost.
17.8.1 Quicksort
Quicksort je najčešće korištena metoda sortiranja. Njome se u prosječnom slučaju postiže
složenost O(n log2 n), a u najgorem slučaju O(n2). To je lošiji rezultat nego kod mergesort
metode, međutim prostorna složenost je manja nego kod mergesort metode, jer se sve operacije
vrše na ulaznom nizu.
Quicksort algoritam koristi metodu podijeli pa vladaj u sljedećem obliku:
Algoritam: Sortiraj niz A[d..g]
PODIJELI. Izaberi jedan element iz niza A[d..g] i zapamti njegovu vrijednost. Taj element
se naziva pivot. Nakon toga podijeli A[d..g] u dva podniza A[d..p] i A[g+1..d] koji imaju
slijedeća svojstva:
Svaki element A[d..p] je manji ili jednak pivotu.
Svaki element A[p+1..g] je veći ili jednak pivotu.
Niti jedan podniz ne sadrži sve elemente (odnosno ne smije biti prazan).
VLADAJ. Rekurzivno sortiraj oba podniza A[d..p] i A[p+1..g], i problem će biti riješen
kada oba podniza budu imala manje od 2 elementa.
Uvjet da nijedan podniz ne bude prazan je potreban jer, kada to ne bi bilo ispunjeno, rekurzivni
problem bi bio isti kao originalni problem, pa bi nastala bekonačna rekurzija.
Podjela na podnizove, tako da budu ispunjeni postavljeni uvjeti, vrši se funkcijom
int podijeli(int *A, int d, int g)
koja vraća indeks podjele na podnizove.
245](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-245-320.jpg)
![Podjela se vrši pomoću dva indeksa (i, j) i pivota koji se proizvoljno odabire, prema pravilu:
• Pomakni i od početka prema kraju niza, dok se ne nađe element A[i] koji je veći ili
jednak pivotu,
• Pomakni j od kraja prema početku niza, dok se ne nađe element A[j] koji je manji ili
jednak pivotu,
• Zatim zamijeni vrijednosti A[i] i A[j], kako bi svaki svaki element A[d..i] bio manji ili
jednak pivotu, a svaki element A[j..g] veći ili jednak pivotu.
Ovaj se proces nastavlja dok se ne dobije da je i > j. Tada je podjela završena, a j označava
indeks koji vraća funkcija. Ovaj uvjet ujedno osigurava da nijedan podniz neće biti prazan.
Postupak je ilustriran na slici 17.6.
Slika 17.6. Postupak podjele niza A[1..6]. Za pivot je
odabran prvi element A[1] vrijednosti 6. Označeni su
indeksi (i,j), a potamnjeni elementi pokazuju koje se
elemente zamjenjuje. Linija podjela je prikazana u slučaju
kada indeks i postane veći od indeksa j.
/* Podijeli A[d..g] u podnizove A[d..p] i A[p+1..g],
* gdje je d <= p < g, i
* A[d..p] <= A[p+1..g].
* Početno se izabire A[d] kao pivot
* Vraća indeks podjele.
*/
int podijeli(int *A, int d, int g)
{
int i = d - 1; /* index lijeve strane A[d..g] */
int j = g + 1; /* index desne strane A[d..g] */
int pivot = A[d]; /* izbor pivot-a */
while (1) {
/* Nadji sljedeći manji indeks j za koji je A[j] <= pivot. */
while (A[--j] > pivot)
{}
/* Nadji sljedeći veći indeks i za koji je A[i] >= pivot. */
while (A[++i] < pivot)
{}
/* Ako je i >= j, raspored je OK. */
246](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-246-320.jpg)
![/* inače, zamijeni A[i] sa A[j] i nastavi. */
if (i < j)
swap(&A[i], &A[j]);
else
return j;
}
}
Pomoću ove funkcije se iskazuje kompletni quicksort algoritam:
/* Sortiraj niz A[d..g] - quicksort algoritmom
* 1.Podijeli A[d..g] u podnizove A[d..p] i A[p+1..g],
* d <= p < g,
* i svaki element A[d..p] je <= od elementa A[p+1..g].
* 2.Zatim rekurzivno sortiraj A[d..p] i A[p+1..g].
*/
void quicksort(int *A, int d, int g)
{
if (d < g) /* završava kada podniz ima manje od 2 elementa */
{
int p = podijeli(A, d, g); /* p je indeks podjele */
quicksort(A, d, p); /* rekurzivno sortiraj A[d..p]*/
quicksort(A, p+1, g); /* rekurzivno sortiraj A[p+1..g]*/
}
}
Analiza složenosti quicksort algoritma
Prvo treba uočiti da je vrijeme za podjelu podnizova od n elemenata, proporcionalno broju
elemenata cn (konstanta c > 0), tj. složenost je O(n). Analizirajmo zatim broj mogućih
rekurzivnih poziva.
Najbolji slučaj
U najboljem slučaju nizovi se dijele na dvije jednake polovine. Pošto je tada ukupan broj
razlaganja jednak log2 n dobije se da je složenost O(n)⋅O(log2 n) = O(n log2 n).
Najgori slučaj
U najgorem slučaju podjela na podnizove se vrši tako da je u jednom podnizu uvijek samo jedan
element. To znači da bi tada nastaje n rekurzivnih poziva, pa je ukupna složenost O(n) ⋅O(n)=
O(n2). Najgori slučaj nastupa kada je niz sortiran ili "skoro" sortiran.
Prosječni slučaj
Analiza prosječnog slučaja je dosta komplicirana. Ovdje se neće izvoditi. Važan je zaključak da
se u prosječnom slučaju dobija složenost koja je bliska najboljem slučaju O(n log2 n).
Postavlja se pitanje: Kako odabrati pivot element?
U prethodnom algoritmu za pivota je odabran početni element A[d]. U praksi se pokazalo
da je znatno povoljnije izbor pivota vršiti po nekom slučajnom uzorku. Recimo, ako se slučajno
247](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-247-320.jpg)
![odabere indeks ix i element A[ix] kao pivot, tada se smanjuje mogućnost da se dobije
nepovoljna podjela kod skoro sortiranih nizova.
Sljedećim postupkom se dobiva vjerojatnost dobre podjele 50%. Odaberu se tri indeksa po
slučajnom uzorku, a zatim se za pivot odabere jedan od ova tri elementa koji je najbliži njihovoj
srednjoj vrijednosti (medijan). Dublje opravdanje ove metode ovdje neće biti dano. Pokazalo se,
da uz primjenu takovog postupka, quicksort predstavlja najbrži poznati način sortiranja nizova,
pa je implementiran u standardnoj biblioteci C jezika.
17.9 Zaključak
Glavna korist od korištenja rekurzije kao programske tehnike je:
• rekurzivne funkcije su jasnije, jednostavnije, kraće, i lakše ih je razumjeti od
odgovarajućih ne-rekurzivnih funkcija, jer najčešće neposredno odgovaraju apstraktnom
algoritmu rješenja problema.
Glavni nedostatak korištenja rekurzije kao programske tehnike je:
• izvršenje rekurzivnih funkcija troši više računarskih resursa od odgovarajućih ne-
rekurzivnih funkcija.
U mnogo slučajeva rekurzivne se funkcije mogu transformirati u ne-rekurzivne funkcije. To se
obavlja jednostavno u slučaju korištenja “repne rekurzije”.
Analiza složenosti algoritama se uglavnom provodi analizom vremena izvršenja programa.
Složenost algoritma se iskazuje “veliki-O” notacijom.
U analizi složenosti algoritama često se koristi princip matematičke indukcije. On se postavlja
na sličan način kao i rekurzivna pravila: definira se temeljni slučaj i pravilo indukcije
(rekurzije).
Kao primjer analize algoritama, analizirano je nekoliko metoda za sortiranje nizova. Pokazano
je da se korištenjem metode “podijeli pa vladaj” dobivaju efikasni algoritmi (quicksort i
mergesort).
248](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-248-320.jpg)





























![if(!dequeue_empty(D))
dequeue_for_each(D, print_elem);
}
int main()
{
int izbor;
char elem[255];
DEQUEUE D = dequeue_new(strcmp, strdup, free);
upute();
printf("? ");
scanf("%d", &izbor);
while (izbor != 0) {
switch(izbor) {
case 1:
printf("Otkucaj ime: ");
scanf("n%s", elem);
dequeue_push_front(D, elem);
printf("%s ubacen u red.n", elem);
dequeue_print(D);
break;
case 2:
printf("Otkucaj ime: ");
scanf("n%s", elem);
dequeue_push_back(D, elem);
printf("%s ubacen u red.n", elem);
dequeue_print(D);
break;
case 3:
if (!dequeue_empty(D)) {
printf("Bit ce %s odstranjen sprijeda.n",
(char *) dequeue_front(D));
dequeue_pop_front(D);
}
dequeue_print(D);
break;
case 4:
if (!dequeue_empty(D)) {
printf("Bit ce %s odstranjen straga.n",
(char *)dequeue_back(D));
dequeue_pop_back(D);
}
dequeue_print(D);
break;
default:
printf("Pogresan Izbor.nn");
upute();
break;
}
printf("n? ");
scanf("%d", &izbor);
}
if(dequeue_find(D, "ivo")) {
278](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-278-320.jpg)














![znakom # )
Leksička analiza je proces kojim se sekvencijalno u nizu ulaznih znakova prepoznaje neki
leksem i gramatički simbol koji on predstavlja, tj. token. Primjerice, leksem "37.5" predstavlja
token NUM. Ako je potrebno, uz token se bilježi i njegova vrijednost, koja predstavlja atribut
tokena.
Leksički analizator se može jednostavno implementirati pomoću funkcije getToken() i
sljedećih deklaracija:
/**************************************************************/
/* datoteka: prefix_lex.h */
/**************************************************************/
#ifndef _PREFIX_LEX_H_
#define _PREFIX_LEX_H_
/* tokeni (terminalni simboli) */
#define NUM 255
#define OPERATOR 256
#define QUIT 257
/* globalne varijable*/
extern FILE *input = stdin; /* ulazni tok */
extern elemT tokenval; /* vrijednost tokena */
extern char lexeme[]; /* leksem tokena */
int getToken();
/* Pri svakom pozivu funkcija vraća sljedeći token iz ulaznog
toka,
ili 0, ako je registriran nepredviđeni znak.
Vrijednost tokena i leksem tokena se zapisuju u globalne
varijable
tokenval i lexeme.
*/
#endif
Implementacija funkcije getToken() je u datoteci "prefix_lex.c".
/**************************************************************/
/* datoteka prefix_lex.c */
/**************************************************************/
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include "lexan.h"
FILE *input = stdin; /* ulazni tok */
elemT tokenval; /* vrijednost tokena */
char lexeme[64]; /* leksem tokena */
int getToken()
{
int ch;
while(1) {
ch = getc(input);
293](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-293-320.jpg)
![/* preskoči bijele znakove */
if(ch == ' ' || ch =='t' || ch =='n' || ch =='r')
continue;
/* zapamti prvi znak */
lexeme[0]=(char)ch; lexeme[1]='0';
if (isdigit(ch)) { /* dobavi broj */
int i = 1; /* prva znamenka je u lexeme[0]*/
ch = getc(input);
while(isdigit(ch) && i<62) {
lexeme[i++]=(char)ch; ch = getc(input);
}
if(ch == '.') {
lexeme[i++]=(char)ch; ch = getc(input);
while(isdigit(ch) && i<62){
lexeme[i++]=(char)ch; ch = getc(input);
}
}
lexeme[i] = '0';
tokenval.num = atof(lexeme);
if (ch != EOF) ungetc(ch,input);
return NUM;
} else if(ch == '+' || ch == '-'
|| ch == '*' || ch == '/' ) {
tokenval.op = ch;
return OPERATOR;
}else if(ch == '(' || ch == ')') {
return ch;
}else if(ch == '$' || ch == EOF) {
return QUIT;
}else if(ch == '#'){ /*komentar do kraja linije */
while (ch != 'n') ch = getc(input);
}else
return 0; /* nedozvoljen znak */
}
}
U funkciji getToken() se unutar petlje dobavlja znak iz toka naredbom getc(input).
Petlja se ponavlja ako su na ulazu "bijeli znakovi" ili ako je dobavljen znak '#', koji označava
početak komentara. U svim ostalim slučajevima petlja se prekida nakon analize dobavljenog
znaka, a analiza se vrši na sljedeći način:
• Ako je dobavljeni znak numerička znamenka, dobavlja se realni broj oblika:
realni_broj : niz_znamenki decimalni_dioopt
decimalni_dio : . niz_znamenki opt
Bilježenje broja se vrši prema prethodnom pravilu: najprije se bilježi niz znamenki, a
zatim, ako iza njih slijedi točka, bilježi se decimalni dio. Leksem broja se bilježi u
stringu lexeme, njegova numerička vrijednost u tokenval.num, a funkcija
getToken() vraća token NUM.
• Ako je dobavljeni znak operator +, -, * ili / , getToken() vraća token OPERATOR,
a vrijednost tokena bilježi u tokenval.op.
• Ako je dobavljeni znak lijeva ili desna zagrada, getToken() vraća ASCII vrijednost
znaka, što služi kao oznaka tokena.
• Ako je dobavljeni znak &, ili ako je kraj datoteke, getToken() vraća token QUIT.
294](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-294-320.jpg)








![t = Izraz();
if(next_token != ')') syn_error(" nedostaje ')' !");
else next_token = getToken();
}
else if( next_token == NUM) {
t = make_numnode(tokenval.num);
next_token = getToken();
}
else if( next_token == OPERATOR && tokenval.op == '-') {
next_token = getToken();
if( next_token == NUM) {
t = make_numnode(-tokenval.num);
next_token = getToken();
}
else
syn_error("krivo unesen broj !");
}
else
syn_error("krivo unesen broj !");
return t;
}
int main(int argc, char **argv)
{
double rez;
TREE t;
if(argc == 2) { /* unos iz datoteke */
input = fopen(argv[1],"r");
if (input == NULL) {
printf("Ne postoji datoteka imena: %s", argv[1]);
exit(1);
}
}
else /* unos tipkovnicom - input == stdin*/
printf(
"Unesite prefiksni aritmeticki izraz ili $ za krajn>");
while (1)
{
t = Naredba();
if( t == NULL) break;
rez = evaluate(t);
if(input == stdin) /* unos tipkovnicom */
printf("nRezultat: %fn>", evaluate(t));
else { /* unos iz datoteke */
print_prefiks (t);
printf("n=%fn", evaluate(t));
}
t = tree_delete(t);
}
if(input != stdin)
fclose(input);
return 0;
}
Program se kompilira komandom:
303](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-303-320.jpg)

![| '/' Clan
Faktor : NUM | - NUM | ( Izraz )
Ovo je LL(1) gramatika i za nju se može napisati rekurzivni silazni parser. Primjerice, funkcija
parsera za pravilo Clan ima oblik:
TREE Clan ()
{
TREE t2, t1;
t1 = Factor();
if(next_token == '*' || next_token = '/') {
int tok = next_token;
t2 = ClanOpt();
return make_tnode(tok, t1, t2);
}
else return t1;
}
TREE ClanOpt()
{
if(is_next_token('*')) {
match('*');
return Clan ();
}
else if(is_next_token('/')) {
match('/');
return Clan ();
}
else syn_error("greška")
}
Napišite ostale funkcije parsera i izvršite potrebne izmjene u leksičkom analizatoru (funkcija
getToken() treba vraćati poseban token za sve operatore i za znak nove linije).
19.4 Stabla s proizvoljnim brojem grana
Ako čvorovi stabla imaju više djece, kao u M-stupanjskom stablu tada se oni mogu opisati
samoreferentnom strukturom Node koja sadrži niz od M pokazivača na djecu čvora.
#define NUM_CHILD M
typedef int elemT:
typedef struct _node {
void * data;
struct _node * child[NUM_CHILD];
} Node;
Čvor se formira pomoću funkcije makeNode():
Node * makeNode( elemT elem, Node *N0, Node *N1,..., Node *Nm)
{
Node *n=(Node *) malloc(sizeof(Node));
if(n) {
n->elem = elem;
n->child[0] = N0;
305](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-305-320.jpg)
![n->child[1] = N1;
.....
n->child[m] = Nm;
}
return n;
}
Ako podstabla imaju različite stupnjeva, zovemo ih višesmjerna stabla (eng. multiway tree). U
tom slučaju može se koristiti prethodna struktura tako da se svi child[i] pokazivači postave
jednakim nuli za i-smjerni čvor. Primjerice, dvosmjerni čvor bi formirali naredbom:
makeNode( elem, N0, N1, NULL,..,NULL);
Loša strana ovakvog pristupa je da se troši memorija za pokazivače nepostojećih čvorova. Taj
se problem može riješiti na dva načina. Prvi je da se i niz child alocira dinamički te da se u
strukturi Node bilježi broj alociranih čorova. Tada struktura Node može biti ovakva:
typedef struct _node {
elemT elem;
int num_child; /*broj alociranih čvorova*/
struct _node **child; /*pokazivač na niz pokazivača*/
} Node;
Drugi način za stvaranje čvorova višesmjernog stabla je da se koriste dva pokazivača. Prvi,
nazvat ćemo ga first_children, pokazuje prvo dijete čvora, a drugi, nazvat ćemo ga
next_sibling pokazuje na listu braće prvog djeteta.
typedef struct _node {
elemT elem;
struct _node *first_child;
struct _node *next_sibling;
} Node;
Dakle, next_sibling je pokazivač glave jednostruko vezane liste, koja sadrži djecu čvora
osim prvog djeteta. Kraj liste se uvijek označava NULL pokazivačem. Za stvaranje čvorova i
uspostavljanje veza među njima mogu poslužiti sljedeće funkcije:
Node *makeLeaf(elemT elem)
{ /*stvaranje lista*/
Node *n= (Node*)malloc(sizeof(Node));
if(n) {
n->first_child = n->next_sibling = 0;
n->elem = elem;
}
return n;
}
Node * make1ChildNode(elemT elem, Node *N1)
{ /*čvor s jednim djetetom*/
Node *n=makeLeaf(elem);
if(n) n->first_child = N1;
return n;
}
Node * make2ChildNode(elemT elem, Node *N1, Node *N2)
{ /*čvor s dva djeteta*/
Node *n=makeLeaf(elem);
if(n) {
306](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-306-320.jpg)
![n->first_child = N1;
N1->next_sibling = N2;
N2->next_sibling = 0;
}
return n;
}
Node * make3ChildNode(elemT elem, Node *N1, Node *N2, Node *N3)
{ /*čvor s tri djeteta*/
Node *n=makeLeaf(elem);
if(n) {
n->first_child = N1;
N1->next_sibling = N2;
N2->next_sibling = N3;
N3->next_sibling = 0;
}
return n;
}
itd.
Veze čvora zapisane u Veze čvora zapisane u Ekvivalentno binarno
Node *child[3]; Node *first-child stablo
Node *next-sibling
1 1 1
/| / /
/ | / 2
/ | / /
2 3 4 2---3---4 5 3
/ | / /
5 6 7 5---6 7 6 4
/ / /
8 9 8---9 7
/
8
a) b) c) 9
Slika 19.9 Tri načina zapisa stabla kojem čvorovi imaju promjenjljivi broj djece. a)
pokazivači čvorova su u nizu child[], b) pokazivači čvorova su first_child i elementi liste
next_sibling, c) ekvivalentno binarno stablo koje se dobije iz drugog oblika rotiranjem
liste čvorova braće za 45o u smjeru okretanja kazaljke sata.
Važno je primijetiti da zapis stabla pomoću first_child i next_sibling čvorova ima
ekvivalentan zapis pomoću binarnog stabla. To je pokazano na slici 19.9. Stablo je oformljeno
naredbama:
Node *N1 = make2ChildNode (7, makeLeaf(8), makeLeaf(9));
Node *N2 = make1ChildNode (4, N1);
Node *N3 = make2ChildNode (2, makeLeaf(5), makeLeaf(6));
Node *N0 = make3ChildNode (1, N3, makeLeaf(3), N2);
Ekvivalentno binarno stablo se dobije iz višesmjernog stabla (first_child-next_sibling tipa)
"rotiranjem" veza next_sibling liste za 45o u smjeru okretanja kazaljke sata.
307](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-307-320.jpg)





![/* umetni element x i povećaj N */
i = pQ->N++;
while (i) {
int parent = (i-1)/2;
if (x.key > pQ->elements[parent].key) break;
pQ->elements[i].key = pQ->elements[parent].key;
i = parent;
}
pQ->elements[i] = x;
}
19.5.2 Brisanje elementa iz prioritetnog reda
Brisanje elementa iz prioritetnog reda se vrši samo na jedan način: briše se element s
minimalnim ključem pomoću funkcije delete_min(). Minimalni element se nalazi u korijenu
stabla, odnosno u hrpi na indeksu 0. Ako ga izbrišemo tada je korijen prazan i u njega treba
zapisati neki drugi element. Najzgodnije je u njega zapisati krajnji element niza i smanjiti
veličinu hrpe. Problem je što tada možda nije zadovoljeno pravilo hrpe. Dovođenje niza u
stanje koje zadovoljava pravilo hrpe vrši se funkcijom heapify(), prema sljedećem algoritmu:
Algoritam: uređenje hrpe kada vrh hrpe nije u skladu s pravilom hrpe
1. Započni s indeksom koji predstavlja vrh hrpe. Spremi taj element u varijablu x. Nadalje
se uzima da je vrh hrpe "prazan".
2. Analiziraj djecu praznog čvora i odredi koje dijete je manje.
3. Ako je ključ od x manji od ključa manjeg djeteta spremi x u prazan čvor i završi,
inače upiši element manjeg djeteta u prazan čvor i postavi da čvor manjeg djeteta bude
prazan čvor. Ponovi korak 2.
void heapify(elemT *elements,int vrh, int N)
{
int min_child, i = vrh;
/*zapamti element kojem tražimo mjesto u hrpi */
elemT x = elements[i];
/* (i) označava "prazni" element*/
while (i < N/2) {
int left = min_child = 2*i+1;
int right = left + 1;
/* Prvo odredi indeks manjeg djeteta - min_child */
if ( (left < N-1)
&& (elements[left].key > elements[right].key) )
min_child = right;
/* Ako je min_child manji od x, upiši ga na prazno
mjesto (i), inače break */
if ( x.key < elements[min_child].key) break;
elements[i] = elements[min_child];
i = min_child;
}
/* konačno stavi x na prazno mjesto*/
elements[i] = x;
}
Sada je implementacija funkcije pqueue_delete_min() jednostavna. u njoj je najprije
zapamćen minimalni element, koji je na indeksu 0, u varijabli minimum. Zatim je krajnji
element upisan na početak niza, a veličina hrpe je smanjena. Slijedi poziv funkcije heapify(),
kojom se uređuje hrpa, ako je poremećeno pravilo hrpe. Postupak brisanja elementa je ilustriran
na slici 19.12.
313](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-313-320.jpg)
![elemT pqueue_delete_min(PQUEUE pQ)
{
elemT minimum;
assert(pQ);
assert( pQ->N > 0 );
/* minimum je u korijenu (indeks 0) */
minimum = pQ->elements[0];
/* zadnji element prebaci u korijen i smanji veličinu hrpe*/
pQ->elements[0] = pQ->elements[--pQ->N];
/* preuredi hrpu od vrha prema dnu (vrh je na indeksu 0) */
heapify(pQ->elements, 0, pQ->N);
return minimum;
}
13
minumum 16 16
X > 16
17 16 17 X > 19 17 x 19
24 21 19 69 24 21 19 69 24 21 31 69
65 26 32 31 X = 31 65 26 32 65 26 32
Slika 19.12 Primjer kako se izvršava operacija delete_min(). Iz reda se odstranjuje ključ 13 koji
je na vrhu hrpe. Strelice pokazuju koje elemente treba pomaknuti da bi se otvorilo mjesto za
element s kraja hrpe ( x=31).
Testiranje se provodi programom "pq-test.c". U programu se najprije 10 slučajno
generiranih brojeva upisuje u prioritetni red pQ, a zatim se briše element po element i ispisuje
vrijednost ključa.
/* Datoteka: pq-test.c*/
/* 1. Generira se 10 slučajnih brojeva i sprema u pqueue
* 2. Briše iz pqueue i ispisuje element po element
*/
#include <stdlib.h>
#include <stdio.h>
#include <memory.h>
#include <assert.h>
#include "pq.h"
int main()
{
int i;
elemT elem;
PQUEUE pQ =pqueue_new(20);
printf("Slucajno generirani brojevi:n");
for(i=0; i<10; i++) {
elem.key = rand() % 100 +1;
pqueue_insert(pQ, elem);
printf("%d ", elem.key);
}
314](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-314-320.jpg)
![printf("nIzlaz iz prioritetnog reda:n");
while(pqueue_size(pQ)) {
elem = pqueue_delete_min(pQ);
printf("%d ", elem.key);
}
pqueue_free(pQ);
printf("n");
return 0;
}
Kada se program izvrši dobije se ispis:
Slucajno generirani brojevi:
42 68 35 1 70 25 79 59 63 65
Izlaz iz prioritetnog reda:
1 25 35 42 59 63 65 68 70 79
Vidimo da je izlaz sortiran, jer smo iz reda brisali jedan po jedan minimalni element.
Vremenska složenost operacija insert() i delete_min() je malena jer se obje operacije provode
samo po jednoj stazi od vrha do dna hrpe ili obrnuto. Kod potpunog stabla duljina staze iznosi
log2(n+1)-1. Pošto nas zanima asimptotska vrijednost (za veliki n), vremenska složenost
iznosi O(log2n).
19.5.3 Sortiranje pomoću prioritetnog reda i heapsort metoda
Prethodni prinjer testiranja ADT PQUEUE pokazuje kako se može izvršiti sortiranje pomoću
prioritetnog reda
Algoritam: sortiranje niza A pomoću prioritetnog reda
1. formiraj objekt tipa PQUEUE pQ.
2. za sve elemente niza A[i], i =0,1,..N-1
pqueue_insert(pQ, A[i])
3. za sve i =0,1,..N-1
A[i] = pqueue_deletemin(pQ);
4. dealociraj objekt pQ
Ovaj algoritam ima vremensku složenost O(n logn), jer se u njemu n puta ponavljaju operacije
umetanja i brisanja, a one imaju složenost O(logn). Loša strana algoritma je da zahtijeva
dodatnu memoriju veličine originalnog niza.
Funkcija heapify() se može efikasno upotrijebiti za sortiranje nizova bez upotrebe
dodatne memorije. Algoritam je jednostavan i primijenjen je u funkciji heapsort(). Sastoji se
od dva koraka. U prvom koraku se od proizvoljnog niza stvara hrpa. Funkcija heapify() se
primjenjuje n/2 puta, na svim unutarnjim čvorovima, najprije na najmanjem podstablu, koji je
trivijalno potpuno stablo, a zatim iterativno na svim većim podstablima do samog korijena. U
drugom koraku se element nultog indeksa (koji je u ovom slučaju minimalan) iterativno
zamjenjuje s krajnjim elementom, a zatim se funkcija heapify() primjenjuje na niz s
umanjenim brojem elemenata.
void heapsort(elemT *A, int N )
{
/* sortira niz A duljine N -> A[i] > A[i+1]*/
int i;
/*1. stvari hrpu od postojeceg niza */
315](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-315-320.jpg)
![for(i = N/2-1; i >= 0; i--)
heapify( A, i, N );
/*2. zamijeni minimum s posljednjim elementom i uredi hrpu */
for(i = N-1; i>0; i-- ) {
elemT tmp = A[i]; A[i]=A[0]; A[0]= tmp;
heapify( A, 0, i);
}
}
Ova verzija heapsort() funkcije sortira nizove od veće prema manjoj vrijednosti. Ako bi
trebali suprotan raspored elemenata tada treba izmijeniti funkciju heapify(), tako da ona
stvara hrpu s najvećim elementom na vrhu hrpe. Izmjena je jednostavna - treba u naredbama
usporedbe zamijeniti operatore < i >.
Vremenska složenost heapsort metode je O(nlog2n) i to u najgorem slučaju, jer se u njoj
funkcija heapify() poziva maksimalno 3n/2 puta. Brzina izvršenja u prosječnom slučaju je
nešto sporija nego kod primjene funkcije quicksort(), ali postoje slučajevi kada
heapsort() daje najveću brzinu izvršenja.
Zadatak: Napišite verziju ADT-a za prioritetni red PQ kojem je na vrhu hrpe element s
maksimalnim ključem.
ADT PQ
insert(Q, x) - ubacuje element x u red Q.
delete_max(Q,) - vraća najveći element reda i izbacuje ga iz reda Q
Operacija nije definirana ako Q ne sadrži ni jedan element, tj
ako je size(Q) = 0.
size(Q) - vraća broj elemenata u prioritetnom redu Q.
19.6 Zaključak
Stabla omogućuju jednostavnu apstrakciju različitih podatkovnih struktura, od slike
porodičnog stabla do jezičkih sintaktičkih i semantičkih veza. U sljedećem poglavlju bit će
pokazano da stabla omogućuju stvaranje općih podatkovnih struktura tipa tablice, rječnika i
skupova.
Stabla se najčešće koriste u obliku binarnog stabla. Pokazano je da se višesmjerna stabla
mogu prikazati ekvivalentnim binarnim stablima.
Pokazana su dva načina programske implementacije stabla. U prvoj se stablo realizira
pomoću samoreferentnih struktura koje sadrže pokazivače, a u drugoj se stablo realizira pomoću
prostih nizova.
Korištenje stabala je uvijek povezano uz neku primjenu za koju se definira potreban skup
operacija. Pokazana je potpuna realizacija interpretera prefiksnih aritmetičkih izraza, a
pokazano je i kako se može napraviti interpreter prefiksnih izraza. Izneseni su temelji
sintaktičke analize jednostavnih jezičkih konstrukcija koje zadovoljavaju LL(1) tip gramatike.
Pokazano je kako se realizira jednostavni leksički analizator i kako se iz BNF notacije
gramatike realizira rekurzivno silazni parser.
Opisana je izvedba apstraktnog tipa podataka PQUEUE kojom se stvaraju prioritetni
redovi. Korištena je struktura tipa hrpe i pomoću nje je realizirana metoda sortiranja koja se
naziva heapsort.
316](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-316-320.jpg)

![Symbol *find(TABLE T, char *key)
{ /* vraća pokazivač simbola ili NULL */
int i;
for (i = 0; i < T->N; i++)
if(!strcmp(T->array[i].key, key);
return &T->array[i];
return NULL;
}
/*sami napišite funkcije insert() i delete()*/
Zbog jednostavnosti uzeto je da je ključ tipa string i da je vrijednost simbola označana
pokazivačem tipa void * (dakle, pokazivačem na bilo koji tip podatka).
Primjer: Implementacija tablice pomoću vezane liste se može temeljiti na sljedećim
strukturama:
typedef struct symbol {
struct symbol *next /* veza u listi */
char * key; /* ključ simbola */
void * val; /* pokazivač vrijednost simbola */
}Symbol;
typedef struct _table {
Symbol *list; /* tablica je lista*/
} *TABLE
Symbol *find(TABLE T, char * key)
{
Symbol *L = T->list;
while( L != NULL) {
if (!strcmp(L->key, key))
return L;
L = L->next;
}
return NULL;
}
U oba slučaja kompleksnost algoritma traženja je O(n) pa ovakova rješenja mogu zadovoljiti
samo za implementaciju manjih tablica. Kada je potrebno imati veće tablice cilj je smanjiti
kompleksnost na O(log n) ili čak na O(1). Ta poboljšanja se mogu ostvariti pomoću tzv. "hash"
tablica i specijano izvedenih stabala za traženje (BST, AVL, RED-BLACK, B-tree). Neke od
ovih struktura upoznat ćemo u ovom poglavlju.
20.2 Hash tablica
Ideju hash2 tablice se može opisati na slijedeći način. Kada u telefonskom imeniku tražimo
neko ime, najprije moramo pronaći stranicu na kojoj je zapisano to ime, a zatim pregledom po
stranici dolazimo do traženog imena. Iskustvo pokazuje da više vremenu treba za traženje
stranice, nego za traženje imena na stranici. Zbog toga se kod telefonskih imenika grupe
stranica označavaju slovima abecede, kako bi se brže pronašla željena stranica. Na sličan način
podaci u hash tablici se grupiraju u više skupova (ili buketa). U kojem skupu se nalaze podaci,
određuje se iz ključa simbola pomoću posebne funkcije koja se naziva hash-funkcija.
2
eng. hash – znači podjelu na manje dijelove, koji su otprilike jednake veličine
318](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-318-320.jpg)
![Definicija: Funkcija hash(k,m) raspodjeljuje argument k u jedan od m skupova, sa statistički
uniformnom razdiobom. Funkcija vraća vrijednost iz intervala i ∈ [0..m-1]. Ta vrijednost
označava da string pripada i-tom skupu.
Postoji više izvedbi hash-funkcije koje zadovoljavaju navedenu definiciju. Za rad sa
stringovima ovdje će biti korišten sljedeći oblik hash-funkcije:
unsigned hash(char *s, unsigned m)
{
/* Argument: s – string
* m - maksimalni broj grupa
* Vraća: hash vrijednost iz intervala [0..m-1]
*/
unsigned x=0;
while(*s != '0') {
s = *s + 31 * x;
k++;
}
return x % m;
}
Može se primijetiti sličnost ove funkcije s funkcijom rand(), koja je opisana u poglavlju
11. Tada je slučajni broj xi , iz intervala [0..n-1], bio generiran iz prethodne vrijednost xi-1,
prema izrazu:
xi = (a * xi-1 + b) % m
gdje su a i b konstante, koje su određene uvjetom da se broj generira sa statistički uniformnom
razdiobom. U slučaju prikazane hash-funkcije ova se zakonitost primjenjuje kumulativno za sve
elemente stringa (a=31, b=*s).
Kada je ključ cjelobrojnog tipa tada se može koristiti funkcija
unsigned hash(int k, unsigned M) {
return k > 0? k % M : - k % M;
}
20.2.1 Otvorena hash tablica
Sada će biti opisana izvedba tablice simbola, koja se naziva otvorena hash-tablica (eng.
Open Hashing ili Separate Chaining). Ilustrirana je na slici 20.1. Otvorena hash tablica se
realizira kao niz koji sadrži pokazivače na liste simbola koje imaju istu hash vrijednost. Te liste
se nazivaju buketi (eng. bucket).
319](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-319-320.jpg)
![Slika 20.1 Hash tablica s vezanom listom
Operacije se provode prema sljedećem pravilu:
insert(k,v) Umetni simbol<k, v> na glavu liste bucket[hash(k, m)].
find (k) Traži simbol ključa k u listi bucket[hash(k, m)]. Vraća
simbol ili NULL
delete(k) Odstrani simbol<k, v> iz liste bucket[hash(k, m)].
Element niza buckets[i] je pokazivač i-te liste. Početno su svi pokazivači jednaki NULL.
Kada u tablici treba tražiti ili unijeti simbol kojem je ključno ime key, to se vrši u listi kojoj je
pokazivač jednak buckets[hash(key,m)].
Slijedi opis implementacije tablice, prema specifikaciji ADT TABLE iz datoteke "table.h".
Specifikacija za generičku hash tablicu
/*Datoteka: table.h */
/*Apstraktni tip TABLE */
typedef struct _table *TABLE;
typedef struct _symbol *SYMBOL;
/* Primjer za string
*/
typedef int (*CompareFuncT)(void *, void *); /* strcmp() */
typedef void *(*CopyFuncT)(void *); /* strdup() */
typedef void (*FreeFuncT)(void *); /* free() */
typedef unsigned (*HashFuncT)(void *, unsigned); /* hash() */
TABLE table_new(unsigned m, CompareFuncT f, HashFuncT h);
/* Konstruktor tablice
* Argument: m - veličina tablice
* f - pokazivač funkcije za poredbu ključa (kao strcmp)
* h - pokazivač hash funkcije (kao hash_str)
* Ako se umjeto pokazivača f i h upiše 0
* podrazumjeva se rad s ključem tipa int
* Vraća: pokazivač tablice ili NULL ako se ne može oformiti tablica
*/
void table_set_alloc(TABLE T, CopyFuncT copykey, FreeFuncT freekey,
CopyFuncT copyval, FreeFuncT freeval);
/* Postavlja pokazivače funkcija za alociranje ključa i vrijednosti
* Argumenti: copykey - pokazivač funkcije za alociranje ključa
* freekey - pokazivač funkcije za dealociranje ključa
* copyval - pokazivač funkcije za alocira vrijednosti
320](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-320-320.jpg)

![{/* Vraća hash vrijednost iz intervala [0..M-1] za string key */
unsigned hashval=0;
char *s = key;
while(*s != '0') {
hashval = *s + 31 * hashval;
s++;
}
return hashval % M;
}
unsigned hash_int(void *p, unsigned M)
{/* Vraća hash vrijednost iz intervala [0..M-1] za cjeli broj p */
/* Prvi argument će biti int, iako je deklariran void *p */
int k = (int)p;
return k > 0? k % M : - k % M;
}
Prema specifikacji ADT TABLE, tablica T, čiji simboli imaju ključ i vrijednost tipa string,
inicijalizira se naredbama:
TABLE T = new_table(1023, strcmp, hash_str);
table_set_alloc(T, strdup, free, strdup, free);
Veličina tablice se odabire proizvoljno. Poželjno je da m bude prosti broj.
Ako je ključ cjelobrojnog tipa inicijalizacija se vrši samo jednom naredbom. Primjerice,
tablicu veličine m=1023, kojoj su ključ i vrijednost tipa int inicijalizira se naredbom:
TABLE T = new_table(1023, 0, 0);
To znači da u implementaciji ADT-a treba predvidjeti automatsko postavljanje funkcije
usporedbe ključeva i hash funkcije za rad s cijelim brojevima, kada su drugi i treći argument
jednaki nuli.
Pored apstraktnog objekta TABLE, specificiran je apstraktni objekt SYMBOL. Ideja je
sljedeća: želimo da su simboli tablice dostupni korisniku. Simboli imaju dva atributa: ključ i
vrijednost. Ako želimo pronaći vrijednost (ili ključ) simbola iz tablice, koristimo najprije
funkciju table_find(), koja vraća tip SYMBOL, a zatim pomoću funkcije
table_symbol_value() ili table_symbol_key(), iz poznatog simbola, dobijemo
pokazivač vrijednosti ili ključa simbola. Primjerice, nakon naredbe
char *v = table_symbol_value(table_find(T, "xxx"));
varijabla v pokazuje string koji je vrijednost simbola koji ima ključ "xxx". Ako ključ "xxx" nije
u tablici varijabla v sadrži NULL pokazivač. Ako simbol sadrži ključ i vrijednost cjelobrojnog
tipa, tada se umjesto pokazivača radi s cijelim brojevima,primjerice
int v = (int) table_symbol_value(table_find(T, 123));
Implementacije ovih funkcija i objekata tipa TABLE i SIMBOL mogu biti različite. Sada
će biti pokazana implementacije otvorene hash tablice, a zatim će biti pokazan drugi tip
implementacije koji se naziva zatvorena hash tablica.
Implementacija otvorene hash tablice
322](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-322-320.jpg)
![/* Datoteka htable1.c */
/* Otvorena hash tablica */
#include <stdlib.h>
#include <string.h>
#include <assert.h>
#include "table.h"
typedef struct _symbol { /* čvor liste simbola */
struct _symbol *next; /* pokazivač vezane liste */
void *key; /* pokazivač ključa simbola */
void *val; /* pokazivač vrijednosti simbola */
}Symbol;
typedef struct _table {
unsigned M; /* veličina tablice */
unsigned N; /* broj simbola u tablici */
Symbol **bucket; /* niz pokazivača na listu simbola */
CompareFuncT compare; /* funkcije usporedbe kljuca */
HashFuncT hash; /* hash funkcija */
CopyFuncT copy_key; /* funkcija alociranja ključa */
CopyFuncT copy_val; /* funkcija alociranja vrijednosti */
FreeFuncT free_key; /* funkcija dealociranja ključa */
FreeFuncT free_val; /* funkcija dealociranja vrijednosti*/
} Table, *TABLE;
static int compareInternal(void *a, void *b)
{ /* usporedba dva integera a i b*/
if( (int)a > (int)b ) return 1;
else if( (int)a < (int)b ) return -1;
else return 0;
}
static unsigned hash_int(void *p, unsigned M)
{/* Vraća hash vrijednost iz intervala [0..M-1] za cjeli broj p */
/* prvi argument će biti int iako je deklariran void *p */
int k = (int)p;
return k > 0? k % M : - k % M;
}
TABLE table_new(unsigned M, CompareFuncT compare, HashFuncT hash)
{
TABLE T = (TABLE) malloc(sizeof(Table));
if (T == NULL) return NULL;
T->M = M;
T->N = 0;
T->bucket = (Symbol **) calloc(M, sizeof(Symbol *) );
T->hash = hash ? hash : hashInternal;
T->compare = compare? compare : compareInternal;
T->free_key = T->free_val = NULL;
T->copy_key = T->copy_val = NULL;
return T;
}
void table_set_alloc(TABLE T, CopyFuncT copykey, FreeFuncT freekey,
CopyFuncT copyval, FreeFuncT freeval)
{
T->copy_key = copykey;
T->copy_val = copyval;
323](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-323-320.jpg)
![T->free_key = freekey;
T->free_val = freeval;
}
static void free_node(TABLE T, Symbol *n)
{
assert(T);
if(n == NULL) return;
/* oslobodi sadržaj čvora: key, val i sam čvor*/
if(T->free_key) T->free_key(n->key);
if(T->free_val) T->free_val(n->val);
free(n);
}
static Symbol *new_node(TABLE T, void *key, void *val)
{
Symbol *np;
assert(T);
np = (Symbol *)malloc(sizeof(Symbol));
if (np == NULL ) return NULL;
np->key =(T->copy_key)? T->copy_key(key) : key;
np->val =(T->copy_val)? T->copy_val(val) : val;
return np;
}
void table_free(TABLE T)
{
unsigned i;
assert(T);
for(i=0; i<T->M; i++) {
Symbol *p, *t;
p = T->bucket[i]; /* glava liste */
while (p != NULL) { /* briše listu iz memorije */
t = p;
p = p->next;
free_node(T, t);
}
}
free(T->bucket); free(T);
}
unsigned table_size(TABLE T)
{ assert(T); return T->N;
}
SYMBOL table_find(TABLE T, void *key)
{
Symbol *p;
assert(T);
p = T->bucket[T->hash(key, T->M)];
while( p != NULL) {
if (T->compare(key, p->key) == 0)
return (void *) p; /* pronađen simbol */
p = p->next;
}
return NULL; /* nije pronađen */
}
void *table_symbol_value(SYMBOL S)
324](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-324-320.jpg)
![{ if(S) return S->val; else return NULL;
}
void *table_symbol_key(SYMBOL S)
{ if(S) return S->key; else return NULL;
}
int table_insert(TABLE T, void *key, void *val)
{
SYMBOL s;
unsigned h;
assert(T);
s = table_find(T, key);
if (s == NULL) { /* ako ne postoji ključ */
Symbol *np = new_node(T, key, val);
if (np == NULL) return 0;
h = T->hash(key, T->M);
np->next = T->bucket[h];
T->bucket[h] = np;
T->N++;
return 1:
}
return 0;
}
int table_delete(TABLE T, void *key)
{
Symbol *p , *prev;
unsigned h = T->hash(key, T->M);
assert(T);
prev = 0;
p = T->bucket[h];
while (p && T->compare(p->key, key)) {
prev = p; p = p->next;
}
if (!p) return 0;
/* p - čvor koji brišemo, prev - prethodni čvor*/
if (prev) prev->next = p->next;
else T->bucket[h] = p->next; /* glava buketa */
--T->N;
free_node (T, p);
return 1;
}
Testiranje se provodi programom hash_test.c. U njemu se formira tablica simbola, i u nju se
unosi nekoliko simbola. Zatim se provjerava da li se simbol "while" nalaze u tablici. Zatim se
taj simbol briše i ponovo provjerava da li je u tablici.
/* Datoteka: hash_test.c*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "table.h"
#include "hash.c"
int main( )
{
char str[20];
SYMBOL s;
325](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-325-320.jpg)

![2. Kvadratično ispitivanje: indeks(k, i) = (hash(k) +i2 ) % m
3. Dvostruko "heširanje" : indeks(k, i) = (hash1(k) +i⋅ hash2(k) ) % m
U sva tri slučaja ispitivanje počinje s indeks(k, 0) = hash(k), a operacije ADT TABLE se mogu
realizirati na sljedeći način:
insert (k,v) - umeće simbol <k,v> u niz htable, prema algoritmu:
Pronađi najmanji i=0,1,.m. za koji htable[indeks(k,i)] nije popunjen
Na tu poziciju upiši simbol <k,v>
find(k) - vraća vrijednost simbola koji ima ključ k, ili null, prema algoritmu:
Algoritam:
Za sve i za koje je redom htable[indeks(k,i)] popunjen,
Ako je ključ simbola htable[indeks(k,i)] jednak k,
Vrati vrijednost simbola
Vrati null
delete(k) - briše simbol koji ima ključ k, prema algoritmu:
Pronađi simbol ključa k
Ako je pronađen, označi da je taj simbol izbrisan
Ilustrirajmo proces linearnog ispitivanja:
U ovom primeru uzet ćemo niz veličine m=10, ključ je cijeli broj i hash funkcija je oblika
hash(k) = k % 10. Početno su sve pozicije prazne, što je označeno simbolom ∅;
0 1 2 3 4 5 6 7 8 9
∅ ∅ ∅ ∅ ∅ ∅ ∅ ∅ ∅ ∅
Ako redom umećemo ključeve 15, 17 i 8, ne postoji preklapanje i rezultat je:
0 1 2 3 4 5 6 7 8 9
∅ ∅ ∅ ∅ ∅ 15 ∅ 17 8 ∅
Umetnimo sada ključ 35. Računamo indeks(k,0) = 35 %10 = 5. Pozicija 5 je zauzeta (s ključem
15), pa moramo ispitati sljedeću poziciju. Indeks(k,1) = (5+1) %10 = 6. Pozicija 6 je slobodna
pa u nju umećemo ključ 35.
0 1 2 3 4 5 6 7 8 9
∅ ∅ ∅ ∅ ∅ 15 35 17 8 ∅
Umetnimo sada ključ 25. Najprije probamo poziciju (25 % 10). Ona je zauzeta. Zatim linearno
ispitujemo sljedeću poziciju 6 ((5+1) % 10). Ona je također zauzeta. Nastavljamo ispitivati
poziciju 7 ((5+2) % 10); ona je zauzeta kao i sljedeća pozicija 8 ((5+3)% 10). Slobodna je tek
pozicija 9 ((5+4) % 10) i u nju umećemo ključ 25.
0 1 2 3 4 5 6 7 8 9
∅ ∅ ∅ ∅ ∅ 15 35 17 8 25
Umetnimo sada ključ 75. Ponovo se ispituje počevši od pozicije 5 (75 % 10). Ispitivanje
pozicija 6, 7, 8 i 9, pokazuje da su one zauzete. Ključ 75 umećemo tek na poziciji 0 ((5+5) %
10), koja je slobodna.
0 1 2 3 4 5 6 7 8 9
75 ∅ ∅ ∅ ∅ 15 35 17 8 25
327](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-327-320.jpg)

![#include <stdlib.h>
#include <string.h>
#include <assert.h>
#include "table.h"
typedef struct _symbol {
void *key; /* pokazivač ključa simbola */
void *val; /* pokazivač vrijednosti simbola */
short status; /* status: prazno(0), */
}Symbol; /* popunjeno(1) ili izbrisano (-1) */
typedef struct _table {
unsigned M; /* veličina tablice */
unsigned N; /* broj elemenata u tablici */
Symbol *htable; /* dinamièki alocirani niz simbola */
CompareFuncT compare; /* funkcije usporedbe kljuèa */
HashFuncT hash; /* hash funkcija */
CopyFuncT copy_key; /* funkcija alociranja kljuca */
CopyFuncT copy_val; /* funkcija alociranja vrrijednosti */
FreeFuncT free_key; /* funkcija dealociranja kljuca */
FreeFuncT free_val; /* funkcija dealociranja vrijednosti */
} Table, *TABLE;
#define KEY(i) (T->htable[(i)].key)
#define VAL(i) (T->htable[(i)].val)
#define EMPTY(i) (T->htable[(i)].status == 0)
#define SET_EMPTY(i) (T->htable[(i)].status = 0)
#define FULL(i) (T->htable[(i)].status == 1)
#define SET_FULL(i) (T->htable[(i)].status = 1)
#define DELETED(i) (T->htable[(i)].status == -1)
#define SET_DELETED(i) (T->htable[(i)].status = -1)
#define NOT_FOUND -1
static int compareInternal(void *a, void *b)
{
if( (int)a > (int)b ) return 1;
else if( (int)a < (int)b ) return -1;
else return 0;
}
static unsigned hashInternal(void *p, int m)
{/* daje hash za integer*/
int k = (int)p;
return (k > 0)? (k % m) : (-k % m);
}
static unsigned prime_list[] =
{ /*niz prostih brojeva*/
7u, 11u, 13u, 17u,
19u, 23u, 29u, 31u,
53u, 97u, 193u, 389u,
769u, 1543u, 3079u, 6151u,
12289u, 24593u, 49157u, 98317u,
196613u, 393241u, 786433u, 1572869u,
3145739u, 6291469u, 12582917u, 25165843u,
50331653u, 100663319u, 201326611u, 402653189u,
805306457u, 1610612741u, 3221225473u, 4294967291u
};
static unsigned get_next_prime(unsigned M)
329](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-329-320.jpg)
![{ /*vraca sljedeci prosti broj*/
int i, len = sizeof(prime_list)/sizeof(unsigned);
for(i=0; i<len; i++) {
if(prime_list[i] >= M)
return prime_list[i];
}
return prime_list[len-1];
}
TABLE table_new(unsigned M, CompareFuncT compare, HashFuncT hash)
{
TABLE T = (TABLE) malloc(sizeof(Table));
if (!T) return NULL;
T->M = get_next_prime(M);
T->N = 0;
T->htable = (Symbol *)calloc(T->M, sizeof(Symbol) );
T->hash = hash ? hash : hashInternal;
T->compare = compare? compare : compareInternal;
T->free_key = T->free_val = NULL;
T->copy_key = T->copy_val = NULL;
return T;
}
void table_set_alloc(TABLE T, CopyFuncT copykey, FreeFuncT freekey,
CopyFuncT copyval, FreeFuncT freeval)
{
T->copy_key = copykey;
T->copy_val = copyval;
T->free_key = freekey;
T->free_val = freeval;
}
void table_free(TABLE T)
{
unsigned i;
short status;
assert(T);
for(i = 0; i < T->M; i++) {
if(FULL(i)) {
if(T->free_key) (*T->free_key)(KEY(i));
if(T->free_val) (*T->free_val)(VAL(i));
}
}
free(T->htable);
free(T);
}
int find_sym_idx(TABLE T, void *key)
{
unsigned i = 0;
unsigned idx = T->hash(key, T->M);
while (1) {
if(EMPTY(idx))
return NOT_FOUND;
if(FULL(idx) && T->compare(KEY(idx), key) == 0)
return idx; /*pronaðen simbol*/
i++;
idx = (idx + (2*i-1)) % T->M;
}
330](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-330-320.jpg)
![return NOT_FOUND;
}
SYMBOL table_find(TABLE T, void *key)
{
int i;
assert(T);
i = find_sym_idx (T, key);
if(i != NOT_FOUND)
return &T->htable[i];
else
return NULL; /* nije pronaðen */
}
void *table_symbol_value(SYMBOL s)
{ if(s) return s->val;
else return NULL;
}
void *table_symbol_key(SYMBOL s)
{ if(s) return s->key;
else return NULL;
}
int table_insert(TABLE T, void *key, char *val)
{
unsigned idx, i = 0;
assert(T);
if(T->N >= T->M/2)
return 0; /*ovdje primijeni rehash funkciju*/
idx = T->hash(key, T->M);
for(;;) /* probaj sljedeći index*/
{
if(!FULL(idx)) {
KEY(idx) = (T->copy_key)? T->copy_key(key) : key;
VAL(idx) = (T->copy_val)? T->copy_val(val) : val;
SET_FULL(idx);
T->N++;
return 1;
}
else if(T->compare(KEY(idx), key) == 0) {
return 0; /* već postoji simbol*/
}
i++;
idx = (idx + (2*i-1)) % T->M;
}
return 0;
}
int table_delete(TABLE T, void *key)
{
int i;
assert(T);
i = find_sym_idx (T, key) ;
if(i != NOT_FOUND && !(DELETED(i))) {
if(T->free_key) T->free_key(KEY(i));
if(T->free_val) T->free_val(VAL(i));
SET_DELETED(i);
--T->N;
331](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-331-320.jpg)

![table_free(T);
return 0;
}
Napomena: Otvorenu hash tablicu inicijalizirajte na veličinu maxrand/2, a zatvorenu tablicu
na veličinu maxrand*2. Mijenjajte veličinu maxrand od 127 do 10000. Primjetit ćete da se
operacije s otvorenom hash tablicom, brže izvršavaju od operacija s zatvorenom tablicom.
Zadatak: U prethodnoj implementaciji zatvorene hash tablice metodom kvadratičnog
ispitivanja izvršte sljedeću izmjenu:
Ukoliko broj simbola u tablice n premaši vrijednost m/2, treba udvostručiti vrijednost
tablice. Na taj način tablica može primiti proizvoljan broj simbola. Za tu svrhu koristite funkciju
table_rehash(T):
TABLE table_rehash(TABLE T )
/* Vraća pokazivač tablice koja ima dvostuko veći kapacitet
* od ulazne tablice T, i koja sadrži simbole it T
*/
{
unsigned int i;
TABLE Tnew;
/* Formiraj uvećanu tablicu i umetni vrijednosti iz T*/
Tnew = table_new( get_next_prime(2*T->M));
for( i=0; i<T->M; i++ )
if(T->htable[i].key != NULL )
table_insert( Tnew, T->htable[i].key,
T->htable[i].val );
free(T->htable ); free(T);
return Tnew;
}
Analizom programerske prakse vidljivo je da se znatno više koristi otvorene tablice. One daju
znatno bolju efikasnost kod visoke popunjenosti tablice.
20.3 BST - binarno stablo traženja
BST je kratica za naziv binarno stablo traženja (eng. binary search tree). Temeljna
karakteristika binarnog stabla traženja je da uvijek sadrži sortirani raspored čvorova. Jedan od
elemenata BST čvora predstavlja jedinstveni ključ. Usporedbom vrijednosti ključa određuje se
red kojim se umeću ili pretražuju čvorovi stabla, prema sljedećoj rekurzivnoj definiciji.
Definicija: Binarno stablo traženja (BST) je:
1. Prazno stablo, ili
2. Stablo koje se sastoji od čvora koji se naziva korijen i dva čvora koji se nazivaju lijevo
i desno dijete, a oni su također binarna stabla (podstabla). Svaki čvor sadrži ključ čija
vrijednost je veća od vrijednosti ključa čvora lijevog podstabla, a manja ili jednaka
vrijednosti ključa čvora desnog podstabla.
333](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-333-320.jpg)


















![o Novi brat od x je bio dijete od w prije rotacije, pa mora bit crn
o Nastavi razmatrati stanje prelaskom na slučajeve 2,3 ili4, u kojima će se, ovisno o
položaju Novog w odrediti da li se Parent(x), koji je crven, pretvara u crni čvor.
Slučaj 2: w je crn i oba djeteta od w su crna
[Napomena: Čvor nepoznate boje označen tankim rubom i slovom s]
o Promijeni boju od w u crveno
o Pomakni promatranje na viši čvor tako da Parent(x) postane Novi x
o Ponovi iteraciju. Iteracija prestaje ako je Novi x = Parent(x) crven (to je uvijek slučaj
ako smo došli iz slučaja 1) Tada se Novi x konačno oboji u crno. Kraj!
Primjetite da je zadržan broj crnih čvorova u stazi od x i u stazi od w. U obje staze najprije
je smanjen broj crnih čvorova, a zatim je na kraju dodan crni čvor.
Slučaj 3: w je crn, lijevo dijete od w je crveno, a desno dijete od w je crno
o Pomijeni boju od w u crveno i boju lijevog djeteta od w u crno
o Desno rotiraj w
o Novi w, tj. novi brat od x je crn s crvenim desnim djetetom
o Proslijedi analizu na slučaj 4
Slučaj 4: w je crn, lijevo dijete od w je crno, a desno dijete od w je crveno
[Napomena: Dva čvora nepoznate boje označeni su slovima s i s'.]
o Postavi boju w jednaku boji Parent(x)
o Postavi boju Parent(x) crno i boju desnog djeteta od w crno
o Zatim lijevo rotiraj Parent(x)
o Pošto je jedan crveni čvor pretvoren u crni (Right(w)), cilj je ispunjen. Završi petlju na
način da postaviš da je x jednak Root(T). Kraj!
Vremensku složenost ovih operacija određuje složenost tri procesa:
352](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-352-320.jpg)
![1. Složenost bst_delete() je O(log2n), jer se traženje vrši u zravnoteženom stablu.
2. Složenost deleteFixup() je određena slučajem 2 jer se jedino u njemu može javiti
potreba za više iteracije. U svakoj iteraciji se analiza podiže jednu razina više, pa je
maksimalno moguće O(log2n) iteracija
3. Slučajevi 1, 3 i 4 imaju samo 1 rotaciju, pa ukupno ne može biti više od 3 rotacije.
Ukupna vremenska složenost je O(log2n) i to s malim konstantnim faktorom. Upravo brzina
operacije brisanja daje crveno-crnom stablu malu prednost nad drugim metodama uravnoteženja
stabla (primjerice, AVL metoda, u najgoram slučaju, kod brisanja vrši O(log2n) rotacija).
Zadatak: Napišite specijaliziranu verziju ADT binarnog stabla koja se od ADT BSTREE
razlikuje po tome da simboli nisu određeni parom <ključ, vrijednost>, već samo sadrže ključ.
Rezultirajući ADT nazovite imenom MULTISET, čime se aludira na skup podataka koji može
sadržavati više istih objekata. Definirajte sve operacije koje postoje kod BST, ali promijenite
imena operacija tako da sva imena počinju prefiksom mset_. Testirajte ADT MULTISET na
problemu sortiranja niza pomoću stabla traženja. Koristite algoritam za sortiranje stablom koji
se obično naziva Treesort, a sastoji se od sljedećih koraka.
Problem: Sotiraj niz A koji sadrži od n objekta tipa T, tako da vrijedi A[i] < A[i+1]
Algoritam:
Inicijaliziraj ADT MULTISET imena Skup, za tip podataka T
Ponavljaj za sve elemente niza A[i], i=0,1, n-1
mset_insert(Skup, A[i])
SYMBOL s ← mset_minimum(Skup);
Ponavljaj za i=0,1, n-1
A[i] ← mset_symbol_key(s)
s ← mset_sucessor(s)
Kraj!
Primjetite da umetanje jednog podatka u stablo traje O(log2n). Pošto ukupno postoji n podataka,
unos u stablo traje O(n log2n). Ispis iz stabla traje O(n). Zaključujemo da sortiranje stablom
(treesort) ima vremensku složenost O(n log2n) + O(n) = O(n log2n). Teorijski ovo je isti
rezultat kao kod Mergesort ili Heapsort metode, ili kao prosječni slučaj složenosti kod
Quicksort metode. U praksi, zbog manjeg konstantnog faktora, preferira se Quicksort metoda.
353](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-353-320.jpg)
![Literatura
[1] American National Standards Institute: American national standard for information
systems—Programming language - C, ANSI X3.159-1989, 1989.
[2] International Standard ISO/IEC 9899: Programming Language C, 1999.
[3] B. W. Kernighan and D. M. Ritchie: The C programming language (2nd ed.), Englewood
Cliffs, NJ: Prentice -Hall, 1988.
[4] D. M. Ritchie: The development of the C language. Second ACM HOPL Conference,
Cambridge, MA. 1993.
[5] R. Sedgewick: Algorithms in C, Addison-Wesley, 1998.
[6] M. A. Weiss: Data Structures and Algorithm Analysis in C, Addison-Wesley, 1997.
[7] T. H. Cormen, C. E. Leiserson and R. L. Rivest: Introduction to Algorithms, MIT Press,
1990.
[8] D. E. Knuth: Sorting and Searching, volume 3 of The Art of Computer Programming,
Addison-Wesley, 1973.
[9] A. V. Aho, J. E. Hopcroft and J. D. Ullman: Data Structures and Algorithms, Addison-
Wesley, 1983.
[10] A. V. Aho, J. E. Hopcroft and J. D. Ullman: Compilers, Addison-Wesley, 1985.
[11] E. Horowitz and S. Sahni: Fundamentals of Computer Algorithms, Computer Science
Press, 1978.
[12] N. Wirth: Algorithms and Data Structures, Prentice Hall, 1986.
[13] A. M. Berman: Data Structures via C++, Oxford Press, 1997.
[13] W. J. Collins: Data Structures and Standard Template Library, McGraw-Hill, 2003.
354](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-354-320.jpg)


![specifikacija-kvalifikacije lista-specifikatoraopt
lista-struct-deklaratora:
struct-deklarator
lista-struct-deklaratora , struct-deklarator
struct-deklarator:
deklarator
deklaratoropt : konstanti-izraz
enum-specifikator:
enum identifikatoropt { enumerator-lista }
enum identifikator
enumerator-lista:
enumerator
enumerator-lista , enumerator
enumerator:
identifikator
identifikator = konstanti-izraz
deklarator:
pokazivačopt direktni-deklarator
direktni-deklarator:
identifikator
(deklarator)
direktni-deklarator [ konstanti-izrazopt ]
direktni-deklarator ( parametari-funkcije )
direktni-deklarator ( lista-identifikatoraopt )
pokazivač:
* lista-specifikacija-kvalifikacijeopt
* lista-specifikacija-kvalifikacijeopt pokazivač
lista-specifikacija-kvalifikacije:
specifikacija-kvalifikacije
lista-specifikacija-kvalifikacije specifikacija-kvalifikacije
parametari-funkcije:
lista-parametara
lista-parametara , ...
lista-parametara:
deklaracija-parametra
lista-parametara , deklaracija-parametra
deklaracija-parametra:
deklaracija-specifikatora deklarator
deklaracija-specifikatora apstraktni-deklaratoropt
lista-identifikatora:
identifikator
lista-identifikatora , identifikator
inicijalizacija:
izraz-pridjele
{ lista-inicijalizacije }
{ lista-inicijalizacije , }
lista-inicijalizacije:
inicijalizacija
lista-inicijalizacije , inicijalizacija
ime-tipa:
lista-specifikatora apstraktni-deklaratoropt
apstraktni-deklarator:
pokazivač
pokazivačopt direktni-apstraktni-deklarator
direktni-apstraktni-deklarator:
( apstraktni-deklarator )
direktni-apstraktni-deklaratoropt [konstanti-izrazopt ]
direktni-apstraktni-deklaratoropt ( parametari-funkcijeopt )
typedef-ime:
identifikator
357](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-357-320.jpg)
![Sintaksa naredbi
naredba: naredba-iteracije:
naredbeni izraz while ( izraz ) naredba
složena-naredba do naredba while ( izraz ) ;
naredba-selekcije for ( izrazopt ; izrazopt ; izrazopt ) naredba
naredba-iteracije
naredba-skoka naredba-selekcije:
označena-naredba if ( izraz ) naredba
naredbeni izraz : if ( izraz ) naredba else naredba
izrazopt ; switch ( izraz ) naredba
složena-naredba : naredba-skoka :
{ lista-deklaracijaopt niz-naredbiopt } goto identifikator ;
lista-deklaracija : continue;
deklaracija break;
lista-deklaracija deklaracija return izrazopt ;
niz-naredbi: označena-naredba:
naredba identifikator: naredba
niz-naredbi naredba case konstanti-izraz : naredba
default : naredba
Sintaksa izraza
primarni-izraz: relacijski-izraz:
identifikator posmačni-izraz
konstanta relacijski-izraz < posmačni-izraz
literalni-string relacijski-izraz > posmačni-izraz
(izraz ) relacijski-izraz <= posmačni-izraz
postfiks-izraz: relacijski-izraz >= posmačni-izraz
primarni-izraz izraz-jednakosti:
postfiks-izraz [ izraz ] relacijski-izraz
postfiks-izraz ( lista-argumenata-opt ) izraz-jednakosti == relacijski-izraz
postfiks-izraz . identifikator izraz-jednakosti != relacijski-izraz
postfiks-izraz -> identifikator
AND-izraz:
postfiks-izraz ++ izraz-jednakosti
postfiks-izraz – AND-izraz & izraz-jednakosti
( ime-tipa ) { lista-inicijalizacije } XOR-izraz:
( ime-tipa ) { lista-inicijalizacije , } AND-izraz
lista-argumenata: XOR-izraz ^ AND-izraz
izraz-pridjele OR-izraz:
lista-argumenata , izraz-pridjele XOR-izraz
unarni-izraz: OR-izraz | XOR-izraz
postfiks-izraz
logički-AND-izraz:
++ unarni-izraz
OR-izraz
-- unarni-izraz logički-AND-izraz && OR-izraz
unarni-operator cast-izraz logički-OR-izraz:
sizeof unarni-izraz logički-AND-izraz
sizeof ( ime-tipa ) logički-OR-izraz || logički-AND-izraz
unarni-operator: uvjetni-izraz:
& | * | + | - | ~ | ! logički-OR-izraz
cast-izraz: logički-OR-izraz ? expr : uvjetni-izraz
unarni-izraz izraz-pridjele:
( ime-tipa ) cast-izraz uvjetni-izraz
multiplikativni-izrazr: unarni-izraz operator-pridjele izraz-pridjele
cast-izraz operator-pridjele:
multiplikativni-izrazr * cast-izraz = | *= | /= | %= | += | -=
multiplikativni-izrazr / cast-izraz | <<= | >>= | &= | ^= | |=
multiplikativni-izrazr % cast-izraz izraz:
aditivni-izraz: izraz-pridjele
multiplikativni-izraz izraz , izraz-pridjele
aditivni-izraz + multiplikativni-izraz konstantni-izraz:
aditivni-izraz - multiplikativni-izraz uvjetni-izraz
posmačni-izraz:
aditivni-izraz
posmačni-izraz << aditivni-izraz
posmačni-izraz >> aditivni-izraz
358](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-358-320.jpg)

![Klučne riječi C - jezika
auto double int struct
break else long switch
case enum register typedef
char extern return union
const float short unsigned
continue for signed void
default goto sizeof volatile
do if static while
Tip operatora Operator Asocijativnost
primarni [] . -> () s lijeva na desno
postfiks –unarni ++ -- s lijeva na desno
prefiks – unarni ++ -- & * + - ~ ! sizeof cast s desna na lijevo
multiplikativni */% s lijeva na desno
aditivni +- s lijeva na desno
posmačni << >> s lijeva na desno
relacijski < > <= >= s lijeva na desno
jednakost == != s lijeva na desno
bitznačajni "i" & s lijeva na desno
ekskluzivni "ili" ^ s lijeva na desno
bitznačajni "ili" | s lijeva na desno
logički "i" && s lijeva na desno
logički "ili" || s lijeva na desno
ternarni uvjetni op. ?: s desna na lijevo
pridjela vrijednosti = *= /= %= += -= <<= >>= &= ^= |= s desna na lijevo
zarez , s lijeva na desno
Prioritet i asocijativnost operatora
360](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-360-320.jpg)


![int putc(int c, FILE *fp);
int fputc(int c, FILE *fp);
Funkcija putc() upisuje znak c u tok fp. Funkcija putchar(c) je ekvivalentna putc(c,
stdout). Funkcija fputc() je ekvivalentna putc(),ali može biti implementirana kao makro
naredba. Sve tri funkcije vraćaju upisani znak, ili EOF u slučaju greške.
printf, fprintf
int printf(const char *format, ...);
int fprintf(FILE *fp, const char *format, ...);
Funkcija fprintf() upisuje tekstualno formatirane argumente u tok fp. Tri točkice
označavaju listu argumenata. Format se određuje u stringu format, koji sadrži znakove koji se
direktno upisuju na izlazni tok i specifikatore formatiranog ispisa argumenata.
printf(format, …) je ekvivalentno fprintf(stdout, format, …).
Specifikator formata se sastoji od znaka %, iza kojeg slijede oznake za širinu i preciznost
ispisa te tip argumenta, u sljedećem obliku:
%[prefiks][širina_ispisa][. preciznost][veličina_tipa]tip_argumenta
Specifikator formata mora započeti znakom % i završiti s oznakom tipa argumenta. Sva ostala
polja su opciona (zbog toga su napisana unutar uglatih zagrada).
U polje širina_ispisa zadaje se minimalni broj kolona predviđenih za ispis vrijednosti. Ako ispis
sadrži manji broj znakova od zadane širine ispisa, na prazna mjesta se ispisuje razmak. Ako
ispis sadrži veći broj znakova od zadane širine, ispis se proširuje. Ako se u ovo polje upiše
znak * to znači da će se broj kolona indirektno očitati iz slijedećeg argumenta funkcije, koji
mora biti tipa int.
Polje prefiks može sadržavati jedan znak koji ima sljedeće značenje:
- Ispis se poravnava prema lijevoj granici ispisa određenog poljem širina_ispisa. (inače se
poravnava s desne strane) U prazna mjesta se upisuje razmak
+ Pozitivnim se vrijednostima ispisuje i '+' predznak.
razmak Ako je vrijednost positivna, dodaje se razmak prije ispisa (tako se može poravnati kolone s
pozitivnim i negativnim brojevima).
0 Mjesta razmaka ispunjuju se znakom 0.
# Alternativni stil formatiranja
Polje . preciznost određuje broj decimalnih znamenki iza decimalne točke kod ispisa realnog
broja ili minimalni broj znamenki ispisa cijelog broja ili maksimalni broj znakova koji se
ispisuje iz nekog stringa. Ovo polje mora započeti znakom točke, a iza nje se navodi broj ili
znak *, koji znači da će se preciznost očitati iz slijedećeg argumenta tipa int. Ukoliko se ovo
polje ne koristi, tada se podrazumijeva da će realni brojevi biti ispisani s maksimalno šest
decimalnih znamenki iza decimalne točke.
Polje tip_argumenta može sadržavati samo jedan od sljedećih znakova znakova:
c Argument se tretira kao int koji se ispisuje kao znak iz ASCII skupa.
d, i Argument se tretira kao int, a ispisuje se decimalnim znamenkama.
e, E Argument je float ili double, a ispis je u eksponentnom formatu.
f Argument je float ili double, a ispis je prostom decimalnom formatu. Ako je prefiks # i
363](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-363-320.jpg)
![preciznost .0, tada se ne ispisuje decimalna točka.
g, G Argument je float ili double, a ispis je prostom decimalnom formatu ili u
eksponencijalnom formatu, ovisno o tome koji daje precizniji ispis u istoj širini ispisa.
o Argument je unsigned int, a ispisuje se oktalnim znamenkama.
p Argument se tretira kao pokazivač tipa void *, pa se na ovaj način može ispisati adresa bilo
koje varijable. Adresa se obično ispisuje kao heksadecimalni broj.
s Argument mora biti literalni string odnosno pokazivač tipa char *.
u Argument je unsigned int, a ispisuje se decimalnim znamenkama.
x, X Argument je unsigned int, a ispisuje se heksadecimalnim znamenkama. Ako se zada
prefiks # , ispred heksadecimalnih znamenki se ispisuje 0x ili 0X.
% Ne odnosi se na argument, već znači ispis znaka %
n Ništa se ne ispisuje, a odgovarajući argument mora biti pokazivač na int, u kojega se upisuje
broj do tada ispisanih znakova
Polje veličina_tipa može sadržavati samo jedan znak koji se upisuje neposredno ispred oznake
tipa.
h Pripadni argument tipa int tretira se kao short int ili unsigned short int.
l Pripadni argument je long int ili unsigned long int.
L Pripadni argument realnog tipa je long double.
Funkcije printf() i fprintf() vraćaju broj ispisanih znakova. Ako nastupi greška, vraćaju
negativan broj.
scanf, fscanf
int scanf(const char *format, ...);
int fscanf(FILE *fp, const char *format, ...);
Funkcijom fscanf() dobavljaju se vrijednosti iz tekstualnog toka fp po pravilima
pretvorbe koji su određeni u stringu format. Te vrijednosti se zapisuju na memorijske
lokacije određene listom pokazivačkih argumenata. Lista argumenata (...) je niz izraza
odvojenih zarezom, čija vrijednost predstavlja adresu postojećeg memorijskog objekta. Tip
objekta mora odgovarati specifikaciji tipa prethodno zapisanog u stringu format.
scanf(format, …) je ekvivalentno fscanf(stdin, format, …).
String format se formira od proizvoljnih znakova i specifikatora formata oblika:
%[prefiks][širina_ispisa][veličina_tipa]tip_argumenta
Ako se pored specifikatora formata navedu i proizvoljni znakovi tada se očekuje da i oni budu
prisutni u ulaznom tekstu (osim tzv. bijelih znakova: razmak, tab i nova linija) . Osim u slučaju
specifikatora %c, %n, %[, i %% , za sve pretvorbe se podrazumijeva da se iz ulaznog teksta
odstrane bijeli znakovi.
Jedini opcioni prefiks je znak '*' koji znači da se pretvorena vrijednost ne dodjeljuje ni
jednom argumentu.
U polju širina_ispisa zadaje se maksimalni broj kolona predviđenih za dobavu vrijednosti.
364](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-364-320.jpg)
![Polje veličina_tipa može sadržavati samo jedan znak koji se upisuje neposredno ispred oznake
tipa pokazivačkog argumenta. To su sljedeći znakovi:
h Pripadni argument tipa int tretira se kao short int ili unsigned short int.
l Pripadni argument je long int ili unsigned long int.
L Pripadni argument realnog tipa je long double.
Polje tip_argumenta može sadržavati samo jedan od sljedećih znakova:
c Dobavlja se jedan znak, a argument je tipa char *. Ako je definirano polje širina_unosa, tada
se unosi onoliko znakova kolika je vrijednost širina_unosa.
d Dobavlja se cijeli broj, a argument je tipa int * ( ili short int * ili long int *, ako
je zadana veličina tipa h ili l).
i Dobavlja se cijeli broj, a argument je tipa int * ( ili short int * ili long int *, ako
je zadana veličina tipa h ili l). Pretvorba se vrši i ako je broj zapisan oktalno (počinje
znamenkom 0) ili heksadecimalno (počinje s 0x ili 0X),
e, E, f,
Dobavlja se realni broj. Argument je tipa float * ili double *.
g, G
o Dobavlja se cijeli broj zapisan oktalnim znamenkama. Argument je tipa unsigned int* (ili
unsigned short int * ili unsigned long int *, ako je zadana veličina tipa h ili
l).
p Dobavlja se pokazivač, a argument mora biti tipa void **.
s Dobavlja se string koji ne sadrži bijele znakove. Argument mora biti tipa char *.
u Dobavlja se cijeli broj, a argument je tipa unsigned int * ( ili unsigned short int
* ili unsigned long int *, ako je zadana veličina tipa h ili l).
x, X Dobavlja se cijeli broj zapisan heksadecimalno. Argument je tipa unsigned int*
Argument je tipa unsigned int* (ili unsigned short int * ili unsigned long
int *, ako je zadana veličina tipa h ili l).
% Ne odnosi se na argument, već znači dobavu znaka %
n Ne vrši se pretvorba. Odgovarajući argument mora biti tipa int *. Upisuje se broj do tada
učitanih znakova
[ Za format oblika %[...] dobavlja se string koji sadrži znakove koji su unutar zagrada, prema
sljedećem obrascu:
%[abc] znači da se dobavlja string koji može sadržavati znakove a,b ili c.
%[a-d] znači da se dobavlja string koji može sadržavati znakove a,b,c ili d.
%[^abc] znači da se dobavlja string koji može sadržavati sve znakove osim a,b ili c.
%[^a-d] znači da se dobavlja string koji može sadržavati znakove sve znakove osim a,b,c ili d.
Argument je tipa char *.
Funkcije scanf()i fscanf() vraćaju broj uspješno izvršenih pretvorbi (bez %n i %*). Ako se
ne izvrši ni jedna konverzija, zbog dosegnutog kraja datoteke, vraća se vrijednost EOF.
gets, fgets
char *fgets(char *buf, int n, FILE *fp);
char *gets(char *buf);
Funkcije fgets() čita liniju teksta (koja završava znakom 'n') iz toka fp, i sprema taj
tekst (uključujući 'n' i zaključni znak '0') u znakovni niz buf. Veličina tog niza je n
znakova. Ako u liniji ima više od n-2 znakova, tada neće biti dobavljeni svi znakovi. Funkcije
gets() je ekvivalentna funkciji fgets(), ali isključivo služi za dobavu stringa s tipkovnice.
365](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-365-320.jpg)











![Ove funkcije pretvaraju multibajt znakovnu sekvencu u tip wchar_t i obrnuto. Funkcija
mbtowc() analizira maksimalno n bajta iz stringa src i pretvara ih u wchar_t i sprema u
dest, te vraća broj bajta ili -1 ako pretvorba nije uspješna.
Funkcija wctomb() pretvara prošireni znak src u multibajt sekvencu dest, i vraća broj bajta u
toj sekvenci.. (Ovaj broj neće nikada biti veći od konstante MB_CUR_MAX, definirane u
<stdlib.h>.)
mbstowcs, wcstombs
size_t mbstowcs(wchar_t *dest, const char *src, size_t n);
size_t wcstombs(char *dest, wchar_t src);
Ove funkcije vrše pretvorbu višestruke multibajt sequence i niza proširenih znakova. Funkcija
mbtowcs() pretvara multibajt sekvencu src i u niz proširenih znakova i sprema u dest, ali
maksimalno n znakova. Vraća broj pretvorenih znakova. Funkcija wcstombs() vrši obrnutu
radnju.
C 5 <math.h>
Standardne matematičke funkcije su deklarirane u zaglavlju <math.h>. Njihov opis je dan
sljedećoj tablici:
Funkcija Vraća vrijednost
double sin(double x); sin(x) , sinus kuta x u radijanima
double cos(double x); cos(x) , kosinus kuta x u radijanima
double tan(double x); tg(x) , tangens kuta x u radijanima
double asin(double x); arcsin(x), vraća vrijednost [-π/2, π/2], za x ∈ [-1,1].
double acos(double x); arccos(x), vraća vrijednost [0, π], za x ∈ [-1,1].
double atan(double x); arctg(x), vraća vrijednost [-π/2, π/2].
double atan2(double y, arctan(y / x), vraća vrijednost [-π,π].
double x);
double sinh(double x); sh(x), sinus hiperbolni kuta x
double cosh(double x); ch(x) , kosinus hiperbolni kuta x
double tanh(double x); th(x) , tangens hiperbolni kuta x
double exp(double x); ex , x potencija broja e = 2,781
double log(double x); prirodni logaritam ln(x), x>0.
double log10(double x); logaritam baze 10, log10(x), x>0.
double pow(double x, xy, potenciranje x s eksponentom y. Nastaje greška ako je
double y); x=0 i y <= 0, ili ako je x<0, a y nije cijeli broj.
double sqrt(double x); √x, za x>=0, dugi korijen pozitivnog broja
double ceil(double x); najmanji cijeli broj (tipa double) koji nije manji od x
double floor(double x); najveći cijeli broj (tipa double) koji nije veći od x
double fabs(double x); |x|, apsolutna vrijednost od x
double ldexp(double x,int n); x*2n
double frexp(double x, rastavlja x na frakcioni dio i eksponent broja 2. Vraća
int *exp); normaliziranu frakciju od x (iz intervala [1/2,1)] i
exponent od 2 u *exp. Ako je x jednak nuli, oba dijela su
jednaka nuli. Primjerice, frexp(2.5, &i) vraća 0.625
(odnosno 0.101 baze 2) i postavlja i na 2, tako da
ldexp(0.625, 2) ponovo daje vrijednost 2.5.
double modf(double x, rastavlja x na integralni i frakcioni dio, tako da oba imaju
double *ip); predznak od x. Vraća frakcioni dio, a integralni dio smješta
u *ip.
double fmod(double x, ostatak dijeljenja realnih brojeva x/y, s predznakom od x.
double y);
377](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-377-320.jpg)






![const char *p;
char tmpbuf[25];
int i;
va_start(argp, format);
for(p = format; *p != '0'; p++) {
if(*p != '%') {
putchar(*p);
continue;
}
switch(*++p)
{
case 'c':
i = va_arg(argp, int); putchar(i);
break;
case 'd':
i = va_arg(argp, int);
sprintf(tmpbuf, "%d", i); fputs(tmpbuf, stdout);
break;
case 'o':
i = va_arg(argp, int);
sprintf(tmpbuf, "%o", i);
fputs(tmpbuf, stdout);
break;
case 's':
fputs(va_arg(argp, char *), stdout);
break;
case 'x':
i = va_arg(argp, int);
sprintf(tmpbuf, "%x", i); fputs(tmpbuf, stdout);
break;
case '%':
putchar('%');
break;
}
}
va_end(argp);
}
C 11 <stddef.h>
U zaglavlju <stddef.h> definirano je nekoliko tipova i makro naredbi.
NULL Makro koji označava konstantu za nul pokazivač (vrijednost mu je 0 ili (void *)0).
size_t Cjelobrojni unsigned tip koji se koristi za označavanje veličine memorijskog
objekta.
ptrdiff_t Cjelobrojni tip koji označava vrijednosti koji nastaju kod oduzimanja pokazivača.
wchar_t Tip “wide character” koji može imati znatno veći interval vrijednosti od tipa char.
Koristi se za multinacionalni skup znakova (Unicode).
offsetof() Makro kojim se računa pomak (eng. offset) u bajtima nekog elementa strukture,
primjerice offsetof(struct tm, tm_year).
Korištenje ovih tipova osigurava prenosivost programa.
C 12 <assert.h>
U zaglavlju <assert.h> definar je makro assert, koji omogućuje testiranje pograma.
384](https://image.slidesharecdn.com/programiranjecjezikom-120306140809-phpapp02/85/Programiranje-c-jezikom-384-320.jpg)










