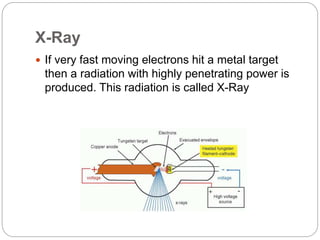
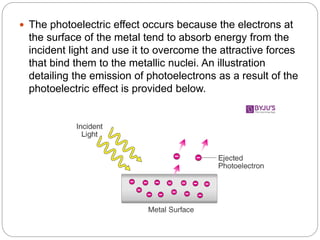
The document discusses several key concepts in physics: 1) It describes the photoelectric effect where electrons are ejected from metals when light is incident, with the kinetic energy of ejected electrons dependent on the frequency of light. 2) It explains that for the photoelectric effect to occur, photons must have sufficient energy to overcome the attractive forces binding electrons. This minimum energy is called the threshold energy. 3) It briefly introduces the Compton effect where the wavelength of scattered photons increases due to collisions with electrons, and de Broglie waves which associate a wavelength to moving particles.

1. Lecturer in physics
Basic Science Division
Mohammad Rashik Zaman

2. X-Ray
 If very fast moving electrons hit a metal target
then a radiation with highly penetrating power is
produced. This radiation is called X-Ray

3. Photoelectric effect
 The photoelectric effect is a phenomenon in
which electrons are ejected from the surface of a
metal when light is incident on it.
 These ejected electrons are
called photoelectrons.
 It is important to note that the emission of
photoelectrons and the kinetic energy of the
ejected photoelectrons is dependent on the
frequency of the light that is incident on the
metal’s surface.
 The process through which photoelectrons are
ejected from the surface of the metal due to the

4.  The photoelectric effect occurs because the electrons at
the surface of the metal tend to absorb energy from the
incident light and use it to overcome the attractive forces
that bind them to the metallic nuclei. An illustration
detailing the emission of photoelectrons as a result of the
photoelectric effect is provided below.

5. Threshold Energy for the
Photoelectric Effect
 For the photoelectric effect to occur, the photons that are incident
on the surface of the metal must carry sufficient energy to
overcome the attractive forces that bind the electrons to the
nuclei of the metals.
 The minimum amount of energy required to remove an electron
from the metal is called the threshold energy (denoted by the
symbol Φ).
 For a photon to possess energy equal to the threshold energy, its
frequency must be equal to the threshold frequency (which is
the minimum frequency of light required for the photoelectric
effect to occur).
 The threshold frequency is usually denoted by the symbol 𝜈th,
and the associated wavelength (called the threshold wavelength)
is denoted by the symbol λth. The relationship between the
threshold energy and the threshold frequency can be expressed
as follows.

6. Compton Effect
 When a high energy photon is scattered due collision
with a target (say electron), the wavelength of the
scattered photon becomes larger than the incident
photon. This phenomenon is called Compton effect.

7. de Broglie Waves
 It is said that matter has a dual nature of wave particles .There is a
wave associated with every moving particle .This is known as de
Broglie matter wave. The wavelength of this wave is called de
Broglie wavelength.
We know that , if the frequency of a photon is f and it has energy of E,
The E= hf , where h= Planck's constant
Or f =
𝐸
ℎ
From relativity it is found that,
E= pc, Where p= linear momentum and c = speed f light
Or, hf = pc
Or, p=
𝑓ℎ
𝑐
Or, p =
ℎ
𝜆
, [𝜆 =
𝑐
𝑓
]
So, 𝜆 =
ℎ
𝑝

8. Heisenberg’s Uncertainty Principle
 Heisenberg’s uncertainty principle states that for particles
exhibiting both particle and wave nature, it will not be possible
to accurately determine both the position and velocity at the
same time.
 If ∆x is the error in position measurement and ∆p is the error
in the measurement of momentum, then
∆x ∆p ≥
ℎ
2𝜋
∆x ∆p ≥ ℏ
where ℏ =
ℎ
2𝜋