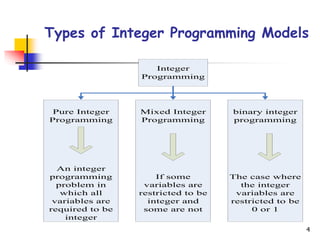
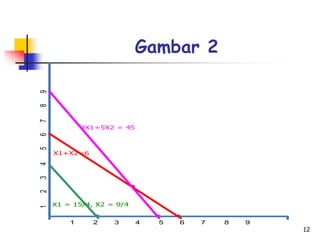
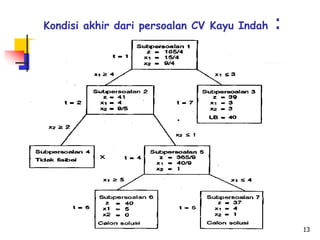
Integer programming (IP) adalah jenis pemrograman linier di mana variabelnya harus berupa bilangan bulat non-negatif, dan lebih sulit diselesaikan dibandingkan pemrograman linier biasa. Model-model integer mencakup pemrograman bilangan bulat, pemrograman campuran, dan pemrograman bilangan biner, dengan teknik penyelesaian yang umum digunakan seperti branch-and-bound dan enumerasi. Contoh praktis menggambarkan penerapan IP dalam optimalisasi keuntungan bagi CV Kayu Indah dalam memproduksi meja dan kursi dengan kendala sumber daya.

1. Integer Programming
DISUSUN OLEH :
IPHOV KUMALA SRIWANA

2. 2
Simply stated, an Integer Programming
problem (IP) is a Linear Programming (LP)
in which some or all the variables are
required to be nonnegative integers.
Integer Programming
Definition:

3. 3
Integer programming problems (IPs) are
usually much harder to solve than linear
programming problems.

4. 4
Integer
Programming
Mixed Integer
Programming
If some
variables are
restricted to be
integer and
some are not
Pure Integer
Programming
An integer
programming
problem in
which all
variables are
required to be
integer
binary integer
programming
The case where
the integer
variables are
restricted to be
0 or 1
Types of Integer Programming Models

5. 5
Types of Integer Programming Models
Models Types of Decision Models
All – integer (IP) All are integers
Mixed-integer (MIP) Some, but not all, are integers
Binary (BIP) All are either 0 or 1

6. 6
Binary integer variables
Binary integer variables can be used to
model yes/no decisions, such as
whether to build a plant or buy a piece
of equipment.

7. 7
Possible Solution Methods
• Branch and Bound
– Will yield the optimal solution
– More efficient than enumeration
• Enumeration
– Will yield the optimal solution
– Time consuming

8. 8
Branch-and-Bound Method
Usually, IPs are solved by some versions of the branch-
and-bound procedure.
Branch-and-bound methods implicitly enumerate all
possible solutions to an IP. By solving a single
subproblem, many possible solutions may be eliminated
from consideration.

9. 9
Contoh 1
(Menyelesalkan Persoalan IP Murni)
 CV kayu indah yang memproduksi meja dan
kursi, menjual produknya dengan keuntungan
Rp. 8.000/unit meja dan Rp. 5.000/unit kursi.
Mengingat perusaahan ini baru dalam
permulaan, saat ini perusahaan hanya mampu
menyediakan maksimum 45m3 kayu setiap
harinya, sedangka jam kerja yang tersedia
tidak lebih dari 6 jam orang per hari. Jika satu
unit meja membutuhkan 1 jam orang dan 9 m3
kayu, sedangkan satu unit kursi membutuhkan
satu jam orang dan 5 m3 kayu. Bagaimanakah
formulasinya agar dapat diperoleh keuntungan
yang maksimum?

10. 10
Contoh 1
Maksimumkan: z = 8 X1 + 5 X2
Pembatas :
X1 + X2 ≤ 6
9 X1 + 5 X2 ≤ 45
X1, X2 ≥ 0 ;
X1, X2 integer

11. 11
Jawaban Contoh 1 :
X1 + X2 = 6
9 X1 + 5 X2 = 45
Maka :
z = 165/4, X1 = 15/4, X2 = 9/4

12. 12
Gambar 2
1 2 3 4 5 6 7 8 9
9X1+5X2 = 45
X1+X2=6
X1 = 15/4, X2 = 9/4
1
2
3
4
5
6
7
8
9

13. 13
Kondisi akhir dari persoalan CV Kayu Indah :

14. 14
Kesimpulan :
1. Jika pencabangan dari suatu subpersoalan
tidak diperlukan, maka subpersoalan itu
adalah fathomed. Ada tiga situasi yang
menyebabkan suatu subpersoalan
fathomed, yaitu:
1. Apabila subpersoalan itu tidak fisibel.
2. Apabila subpersoalan itu memberikan solusi
optimal di mana seluruh variabelnya berharga
integer.
3. Apabila nilai z-optimal untuk subpersoalan itu
tidak lebih baik dari nilai z-optimal subpersoalan
lain (dalam persoalan maksimasi berarti nilai z-
optimal dari subpersoalan itu tidak lebih besar
daripada batas bawah yang telah diperoleh).

15. 15
Kesimpulan :
2. Suatu subpersoalan dapat diabaikan
(dieliminasi dari pertimbangan selanjutnya)
apabila subpersoalan itu berada dalam
situasi berikut:
• Tidak fisibel. Dalam contoh CV Kayu Indah,
subpersoalan 4 diabaikan karena alasan ini.
• Batas bawah atau L8 (yang menyatakan nilai z
dari calon solusi terbaik) sekurang-kurangnya
berharga sama besar dengan nilai z dari
subpersoalan yang bersangkutan. Pada contoh
CV Kayu Ihdah, subpersoalan 3 dan 7 diabaikan
karena alasan ini.