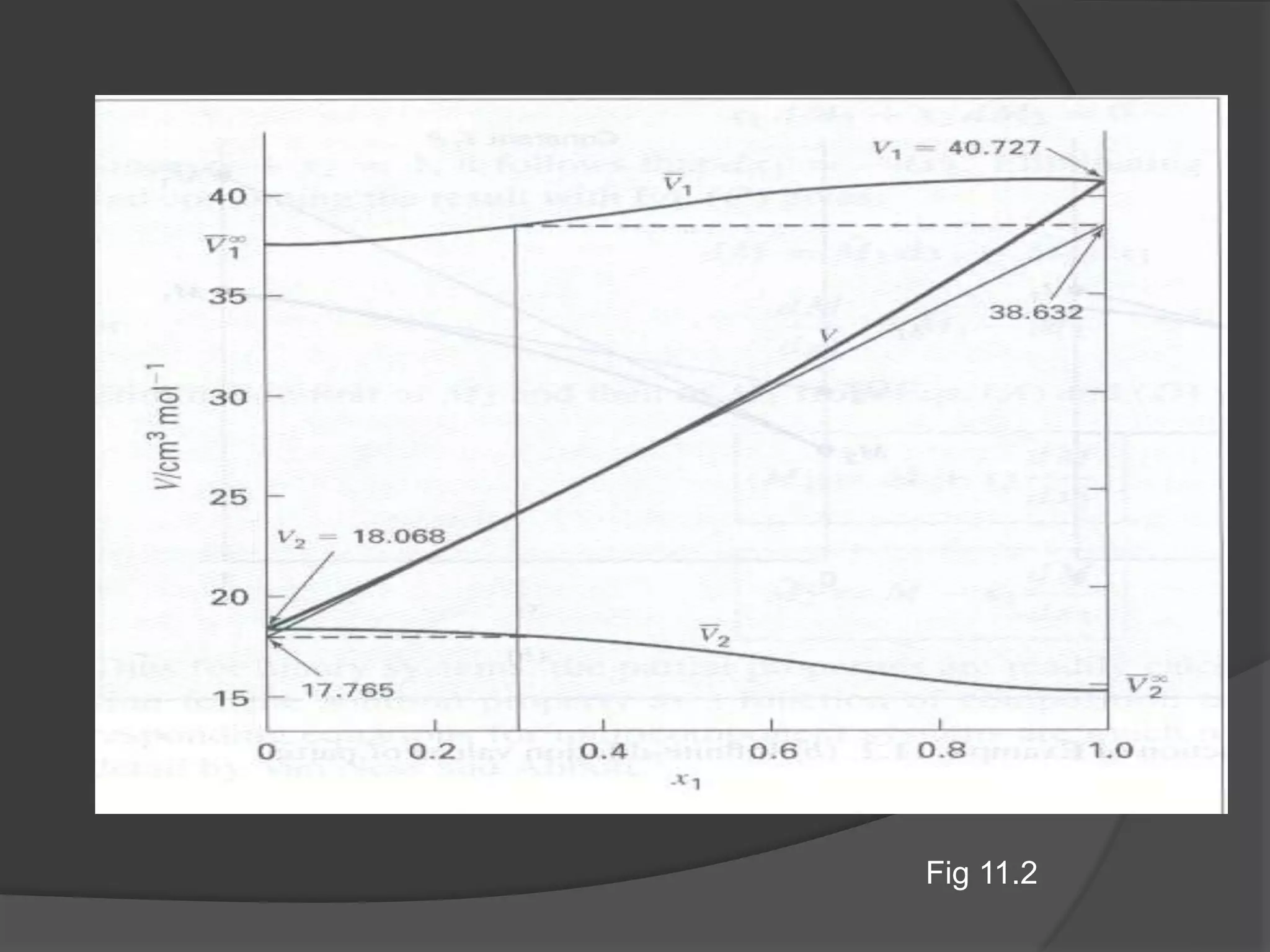
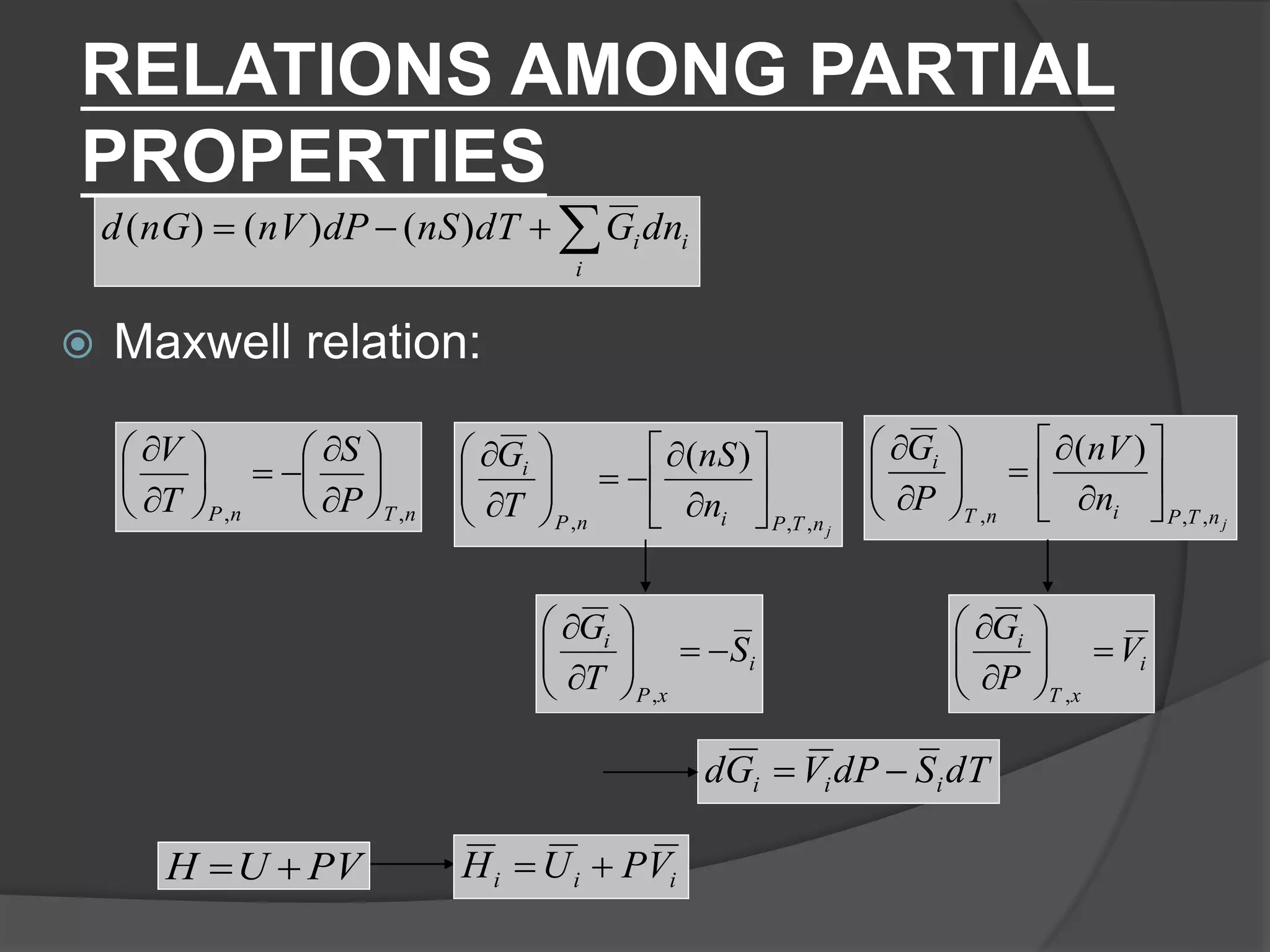
El documento describe las propiedades molares parciales de las especies en soluciones, destacando que estas propiedades termodinámicas reflejan cómo varía una propiedad extensa en función de la composición molar del sistema a temperatura y presión constantes. Se explican ejemplos con agua y etanol, así como el uso de la ecuación de Gibbs-Duhem para soluciones binarias y su influencia en puntos de ebullición y entalpías. También se presentan relaciones entre propiedades parciales mediante ecuaciones termodinámicas relevantes.

2. PARTIAL PROPERTIES
 Define the partial molar property of species i
jnTPi
i
n
nM
M
,,
)(









• A partial molar property is a thermodynamic quantity which indicates how
an extensive property of a solution or mixture varies with changes in
the molar composition of the mixture at constant temperature and pressure.
• When one mole of water is added to a large volume of water at 25 °C, the volume
increases by 18 cm3. The molar volume of pure water would thus be reported as
18 cm3 mol−1. However, addition of one mole of water to a large volume of
pure ethanol results in an increase in volume of only 14 cm3.
• The reason that the increase is different is that the volume occupied by a given number
of water molecules depends upon the identity of the surrounding molecules. The value
14 cm3 is said to be the partial molar volume of water in ethanol.

3. THE GIBBS/DUHEM EQUATION
 Define the partial molar property of species
i:
 the chemical potential and the particle molar
Gibbs energy are identical:
 for thermodynamic property M:
jnTPi
i
n
nM
M
,,
)(









ii G
,...),...,,,,( 21 innnTPMnM 

















i
ii
nPnT
dnMdT
T
M
ndP
P
M
nnMd
,,
)(

4. 
















i
ii
nPnT
dnMdT
T
M
ndP
P
M
nnMd
,,
)(
 
















i
iii
nPnT
ndxdnxMdT
T
M
ndP
P
M
nMdnndM )(
,,
0
,,































  dnMxMndxMdT
T
M
dP
P
M
dM
i
ii
i
ii
nPnT
0
,,
















 i
ii
nPnT
dxMdT
T
M
dP
P
M
dM and 0 i
ii MxM
Calculation of mixture
properties from partial
properties
0 i
ii MnnM
0
,,
















i
ii
nPnT
MdxdT
T
M
dP
P
M
 
i
ii
i
ii dxMMdxdM
The Gibbs/Duhem equation

5. •Binary solution is a mixture of two liquids that are
completely miscible one with another. The boiling point
of binary solution depends upon the solution
composition and there can be three cases:
1. the boiling points of solutions of all compositions lie
between the boiling points of clean liquids
2. the boiling points of solutions of any composition lie
above the boiling points of clean liquids
3. the boiling points of solutions of some compositions
lie below the boiling points of clean liquids
WHAT IS BINARY SOLUTION

6. PARTIAL PROPERTIES IN
BINARY SOLUTION
 For binary system
2211 MxMxM 
22221111 dxMMdxdxMMdxdM 
Const. P and T, using Gibbs/Duhem equation
2211 dxMdxMdM 
121  xx
21
1
MM
dx
dM

1
21
dx
dM
xMM 
1
12
dx
dM
xMM 

7. 2211 VxVxV  molcmV /025.24)765.17)(7.0()632.38)(3.0( 3

mol
V
V
n
t
246.83
025.24
2000

moln 974.24)246.83)(3.0(1 
moln 272.58)246.83)(7.0(2 
3
111 1017)727.40)(974.24( cmVnV t
 3
222 1053)068.18)(272.58( cmVnV t

EXAMPLE : 1
The need arises in a laboratory for 2000 cm3 of an antifreeze solution consisting of
30 mol-% methanol in water. What volumes of pure methanol and of pure water at
25°C must be mixed to form the 2000 cm3 of antifreeze at 25°C? The partial and
pure molar volumes are given.
Methanol (1): V1 = 38.632 cm3 /mol V1 = 40.727 cm3 /mol
Water (2) : V2 = 17.765 cm3 /mol V2 = 18.068 cm3 /mol
The total number of moles required is :
Now, Volume of the each species:

8. Fig 11.2

9. The enthalpy of a binary liquid system of species 1 and 2 at fixed T and P is:
Determine expressions for and as functions of x1, numerical values for the pure-
species enthalpies H1 and H2, and numerical values for the partial enthalpies at infinite
dilution and
1H 2H

1H

2H
)2040(600400 212121 xxxxxxH 
)2040(600400 212121 xxxxxxH 
121  xx
3
11 20180600 xxH 
1
21
dx
dH
xHH 
3
1
2
11 4060420 xxH 
121  xx
3
12 40600 xH 
01 x
mol
J
H 4201 

11 x
mol
J
H 6402 

EXAMPLE : 2

10. RELATIONS AMONG PARTIAL
PROPERTIES
 Maxwell relation:

i
iidnGdTnSdPnVnGd )()()(
nTnP P
S
T
V
,,
















jnTPinP
i
n
nS
T
G
,,,
)(
















jnTPinT
i
n
nV
P
G
,,,
)(
















i
xP
i
S
T
G








,
i
xT
i
V
P
G








,
PVUH 
dTSdPVGd iii 
iii VPUH 

11.  Every equation that provides the linear
relation among thermodynamics
properties if a constant composition
solution has as it’s counterpart an
equation connecting corresponding
partial properties of each species in that
solution.

12. THANK YOU