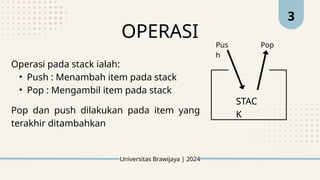
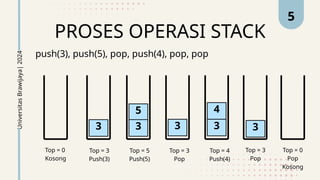
Dokumen ini menjelaskan tentang struktur data stack yang mengikuti prinsip LIFO (Last In First Out) dan mencakup operasi dasar seperti push dan pop. Selain itu, terdapat penjelasan mengenai notasi matematika seperti notasi polish, infix, dan postfix beserta algoritma konversinya. Contoh kode dalam Java juga disediakan untuk menggambarkan penggunaan stack.

1. STACK
By : Rahimi Illong Tabayuni
Universitas Brawijaya | 2024

2. • Stack (tumpukan) adalah struktur data yang berbentuk
tumpukan dimana penambahan dan penghapusan
elemen dilakukan pada satu ujung yang sama.
• Mengikuti konsep LIFO (Last In First Out)
• Elemen yang terakhir kali masuk akan menjadi elemen
yang pertama keluar.
Universitas Brawijaya | 2024
STACK
1

3. CONTOH
Universitas Brawijaya | 2024
2
Tumpukan
Buku
Tumpukan
Piring
Tumpukan
Uang

4. Universitas Brawijaya | 2024
OPERASI
3
Operasi pada stack ialah:
• Push : Menambah item pada stack
• Pop : Mengambil item pada stack
Pop dan push dilakukan pada item yang
terakhir ditambahkan
Pus
h
Pop
STAC
K

5. OPERASI
Menghapus elemen teratas dari
stack
Pop
Mengecek elemen teratas dari
stack tanpa menghapusnya
Universitas
Brawijaya
|
2024
Peek/ Top
4
Memeriksa apakah stack
kosong atau tidak
isEmpty()
Mengembalikan jumlah elemen
dalam stack
size()

6. PROSES OPERASI STACK
Universitas
Brawijaya|
2024 5
5
push(3), push(5), pop, push(4), pop, pop
Top = 0
Kosong
3
4
3
3
3
3
Top = 3
Push(3)
Top = 5
Push(5)
Top = 3
Pop
Top = 4
Push(4)
Top = 3
Pop
Top = 0
Pop
Kosong

7. LATIHAN
Universitas Brawijaya | 2024
import java.util.Stack;
public class Stack{
public static void main(String args[]) {
// membuat objek dari kelas stack
Stack s = new Stack();
// menambah elemen pada stack
s.push(1); // integer
s.push(‘A’); // char
s.push(“ABC”); // string
s.push(true); // boolean
System.out.println(s);
}
}
6

8. LATIHAN
Universitas Brawijaya | 2024
import java.util.Stack;
public class Test {
public static void main(String args[]) {
// membuat objek dari kelas stack
Stack s = new Stack();
// menambah elemen pada stack
s.push(1); // integer
s.push(‘A’); // char
s.push(“ABC”); // string
s.push(true); // boolean
System.out.println(s);
}
}
7
Hasil: [1, A, ABC,
true]

9. LATIHAN 2
public static void main(String args[]) {
// membuat objek dari kelas stack
Stack s = new Stack();
// menambah elemen pada stack
s.push(‘A’);
s.push(‘S’);
s.push(‘D’);
s.push(‘T’);
s.push(‘I’);
s.push(‘D’);
//menghapus elemen
s.pop();
s.pop();
System.out.println(s);
}
8

10. LATIHAN 2
public static void main(String args[]) {
// membuat objek dari kelas stack
Stack s = new Stack();
// menambah elemen pada stack
s.push(‘A’);
s.push(‘S’);
s.push(‘D’);
s.push(‘T’);
s.push(‘I’);
s.push(‘D’);
//menghapus elemen
s.pop();
s.pop();
System.out.println(s);
}
9
Hasil: [A, S, D, T]

11. LATIHAN 3
// membuat objek dari kelas stack
Stack s = new Stack();
// menambah elemen pada stack
s.push(“ASD”);
s.push(“TI”);
s.push(‘D’);
s.push(“DIDDY”);
s.push(“MCGONAGALL);
// melihat elemen terakhir pada stack
System.out.println(s.peek());
10

12. LATIHAN 3
// membuat objek dari kelas stack
Stack s = new Stack();
// menambah elemen pada stack
s.push(“ASD”);
s.push(“TI”);
s.push(‘D’);
s.push(“DIDDY”);
s.push(“MCGONAGALL);
// melihat elemen terakhir pada stack
System.out.println(s.peek());
11
Hasil: MCGONAGALL

13. NOTASI POLISH
Notasi polish adalah cara
menuliskan ekspresi
matematika di mana operator
(+, -, *, /) ditempatkan di depan
operand (angka yang
dioperasikan).
Universitas
Brawijaya
|
2024
Infix
Operator ditempatkan di
tengah/ di antara operand.
Postfix
Operator ditempatkan setelah
operand.
12
Contoh: A + B, 3 - 2
Contoh: A B +, 3 2 -

14. OPERATOR PRIORITY
Universitas
Brawijaya
|
2024 13
^ Pangkat, akar
/ dan *
Pembagian dan
Perkalian
+ dan -
Penambahan dan
Pengurangan

15. INFIX KE POSTFIX
14
Misal :
Q = ekspresi dalam notasi infix
P = ekspresi dalam notasi postfix
Algoritma:
1.Push tanda “(” ke stack dan tambahkan tanda “)” di akhir Q.
2.Scan Q dari kiri ke kanan
3.Jika yang discan adalah operand, maka tambahkan ke P.
4.Jika yang discan adalah “(”, maka push ke stack.
5.Jika yang discan adalah “)”, maka pop isi stack sampai ditemukan tanda “(”, kemudian
tambahkan ke P namun tanda “(” tidak disertakan ke P.
6.Jika yang discan adalah operator, maka:
• Jika elemen paling atas dari stack adalah operator yang mempunyai tingkat yang sama
atau lebih tinggi dari operator yang discan, maka pop operator tersebut dan tambahkan
ke P
• Push operator ke stack
1.Selesai

16. INFIX KE POSTFIX
15
A + ( B * C - ( D / E ^ F ) * G ) * H )
1 2 3 4 5 6 7 8 9 10 11
1
2
1
3
14 15 16 17 18 19 20
CONTOH:
Q = A + ( B * C - ( D / E ^ F ) * G ) * H
Tambahkan “)” pada notasi Q
sehingga:
Q :
No

17. 16
No Simbol Stack Ekspresi P
(
1 A ( A
2 + (+ A
3 ( (+( A
4 B (+( AB
5 * (+(* AB
6 C (+(* ABC
7 - (+(- ABC*
8 ( (+(-( ABC*

18. 17
No Simbol Stack Ekspresi P
9 D (+(-( ABC*D
10 / (+(-(/ ABC*D
11 E (+(-(/ ABC*DE
12 ^ (+(-(/^ ABC*DE
13 F (+(-(/^ ABC*DEF
14 ) (+(- ABC*DEF^/
15 * (+(-* ABC*DEF^/
16 G (+(-* ABC*DEF^/G
17 ) (+ ABC*DEF^/G*-

19. 18
No Simbol Stack Ekspresi P
18 * (+* ABC*DEF^/G*-
19 H (+* ABC*DEF^/G*-H
20 ) ABC*DEF^/G*-H*+
HASIL AKHIR POSTFIX:
P = ABC*DEF^G*-H*+

20. POSTFIX
19
Misal :
P = Ekspresi matematika yang ditulis dalam notasi
postfix
Algoritma:
1.Tambahkan tanda “)” di akhir P.
2.Scan P dari kiri ke kanan
3.Jika yang discan adalah operand, maka push ke stack.
4.Jika yang discan adalah operator (opr), maka:
• Pop 1 buah elemen teratas dari stack, simpan dalam variabel var1
• Pop 1 buah elemen teratas dari stack, simpan dalam variabel var2
• Hitung variabel (var2 opr var1), simpan hasil di variabel hitung
• Push variabel hitung ke stack
1.Pop isi stack dan simpan di nilai variabel
2.Selesai

21. MENGHITUNG NOTASI POSTFIX
20
5 2 6 + * 12 4 / - )
1 2 3 4 5 6 7 8 9 10
CONTOH:
P = 5, 2, 6, +, *, 12, 4, /, -
Tambahkan “)” pada notasi P
sehingga:
P = 5, 2, 6, +, *, 12, 4, /, -, )
P :
No

22. 21
No Simbol Stack
Operasi
Perhitungan
1 5 5
2 2 5, 2
3 6 5, 2, 6
4 + 5, 8
var1=6, var2=2, hitung= 2
+ 6 =8
5 * 40
var1=8, var2=5, hitung= 5
* 8 =40
6 12 40, 12
7 4 40, 12, 4
8 / 40, 3
var1=4, var2=12, hitung=
12 / 4 = 3
var1=3, var2=40, hitung= 40 -

23. THANK YOU
Universitas Brawijaya | 2024