Dokumen ini membahas tentang struktur data tumpukan (stack), termasuk definisi, karakteristik, dan operasi dasar seperti push, pop, dan pengecekan status stack. Selain itu, dijelaskan cara implementasi stack menggunakan array dan linked list, serta aplikasi stack dalam berbagai konteks seperti web browser dan pemrosesan struktur bersarang. Terdapat juga perbandingan antara notasi infix, postfix, dan prefix dalam ekspresi aritmatika.

1. Struktur Data
Stack
Dibuat oleh : kelompok 5
Anggota : - Riani Agustiani
- Rhalas Fadilah
- Desty Yuliyani
- Aisyah N A Z
- Meli Saptari
- Pemi Ningsih

2. STACK
Definisi
Stack
Operasi
dasar Stack
Pengimpleme
ntasian pada
linked list
Karakteristik
stack
Pengimpleme
mntasian
pada Array
Aplikasi
Stack

3. STACK (TUMPUKAN)
 Stack merupakan kumpulan item yang ditumpuk,
dimana data hanya bisa di akses dari data yang
paling atas atau TOP.
 Struktur data linear dimana hanya terjadinya proses
hanya di TOP baik push maupun pop.
 Bisa diimplementasikan menggunakan array atau
Linked List.
 Bersifat LIFO = Last In First Out dimana data yang
terakhir masuk adalah data yang pertama keluar.

5. Penggunan Stack
 History pada web browser.
 Undo Log pada text editor.
 Pemrosesan struktur bersarang (nested) :
loop, rekursi, fungsi, dll.
 Algoritma back tracking – Artificial
Intelegence

6. Operasi-operasi stack
 Push : digunakan untuk menambah item pada stack
pada tumpukan paling atas
 Pop : digunakan untuk mengambil item pada stack
pada tumpukan paling atas
 · Clear : digunakan untuk mengosongkan stack
 IsEmpty : fungsi yang digunakan untuk mengecek
apakah stack sudah kosong

7.  : fungsi yang digunakan untuk mengecek
apakah stack sudah penuh
 Retreive : Untuk mendapatkan nilai dari
item teratas.

8. Operasi Dasar Stack
 Push : memasukkan sebuah item baru ke
dalam stack.
 Pop : mengeluarkan sebuah item dari
stack.
 Operasi lain : Is_Empty, Is_Full, Top
Note : pop dan push dilakukan di TOP

9. Karakteristik Stack
 Data hanya dapat dimasukan pada
posisi top/ atas stack
 - Data hanya dapat dihapus pada posisi
top stack
 - Data tidak dapat dihapus dari tengah-
tengah data stack tanpa memindahkan
item yang ada pada atasnya terlebih
dahulu.

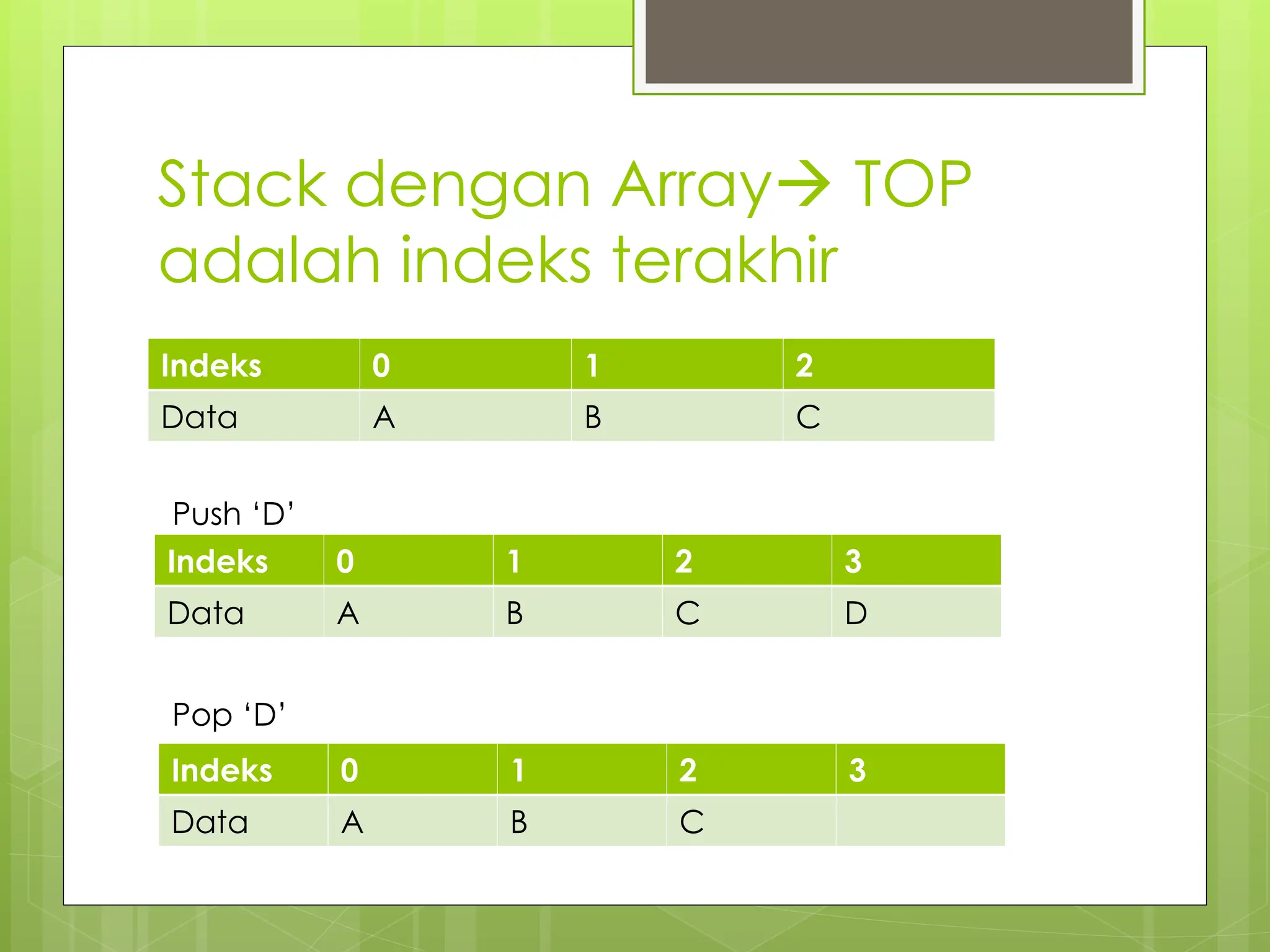
10. Pengimplementasian Stack
Pada Array
 Pengimplementasian stack pada array dapat
dilakuka apabila jumlah elemen maksimum
diketahui, dan pastikan array yang di
deklarasikan cukup untuk menyimpan data
atau elemen maksimum pada stack.
 Pendeklarasian pada array contoh : int stack
[100];
 Pendeklarasian variabel digunakan untuk
penyimpan indeks terakhir contoh : int top;

11. Stack dengan Array TOP
adalah indeks terakhir
Indeks 0 1 2
Data A B C
Push ‘D’
Indeks 0 1 2 3
Data A B C D
Pop ‘D’
Indeks 0 1 2 3
Data A B C

12. Stack dengan Linked List
 Jika sebuah linked list SELALU
menambahkan node baru dan
menghapus node lama dari salah SATU
ujungnya saja (posisi Head ataukah Tail)
 STACK.
 How?

13. Push Operation
 Identik dengan operasi prepend

14. Pop Operation
 Identik dengan operasi delfirst

15. Ekspresi Aritmatika
 Ekspresi aritmatika umumnya ditulis dalam bentuk
infix.
 Contoh :
A+B
A-C+B
A+((B*C)/D)
 Komputer lebih mudah mengevaluasi ekspresi postfix,
karena tidak perlu mengelompokkan subekspresi
kedalam tanda kurung.
APLIKASI STACK

16. Infix, Postfix, dan Prefix
Infix
Infix Postfix
Postfix Prefix
Prefix
A*B
A*B AB*
AB* *AB
*AB
A*(B+C)
A*(B+C) ABC+*
ABC+* *A+BC
*A+BC
(A*B)+C
(A*B)+C AB*C+
AB*C+ +*ABC
+*ABC
A+((B*C)/D)
A+((B*C)/D) ABC*D/+
ABC*D/+ +A/*BCD
+A/*BCD
(A^2+B^2)*(C-D)
(A^2+B^2)*(C-D) A2^B2^+CD-*
A2^B2^+CD-* *+^A2^B2-CD
*+^A2^B2-CD

17. TERIMAKASIH