IK
Uploaded byIgnat Korchagin
PDF, PPTX1,540 views

Overview and evolution of password-based authentication schemes

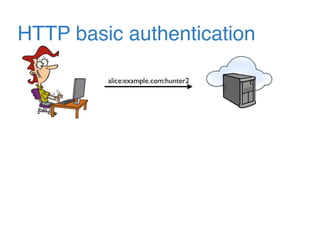
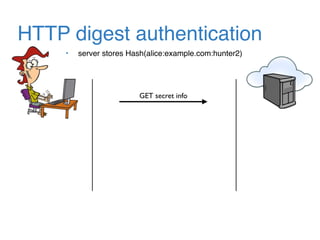
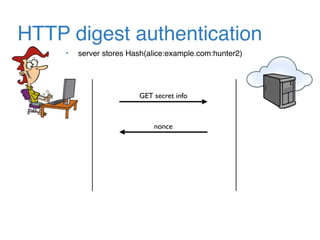
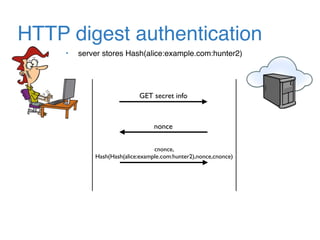
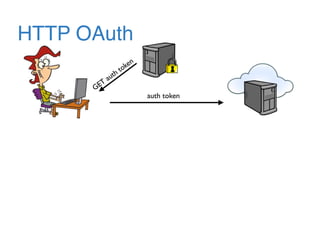
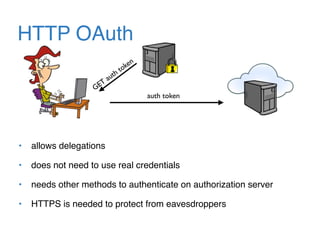
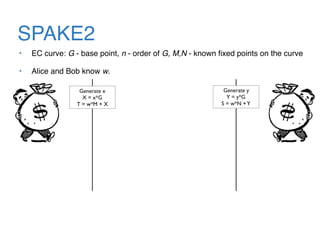
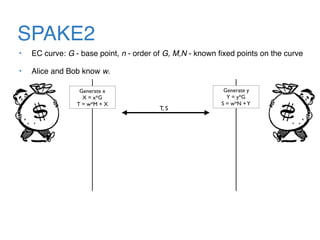
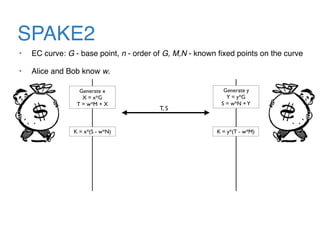
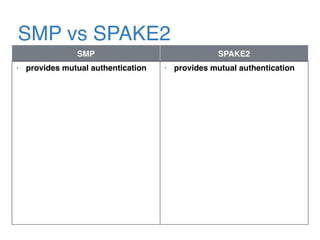
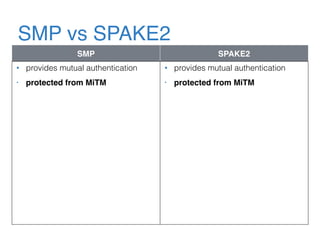
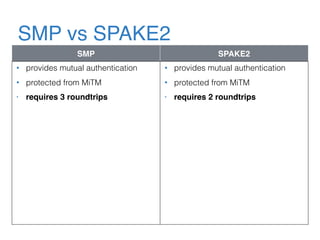
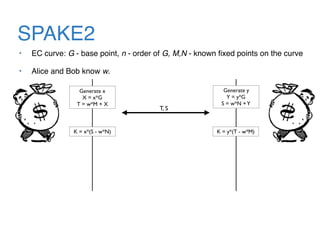
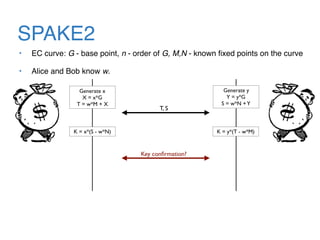
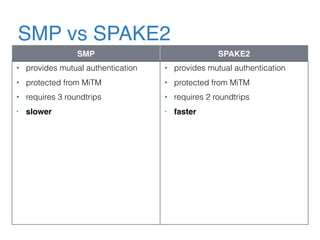
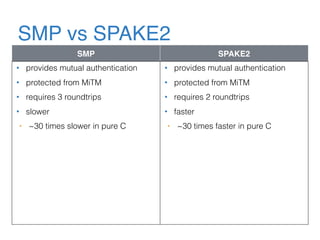
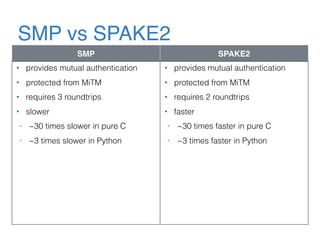
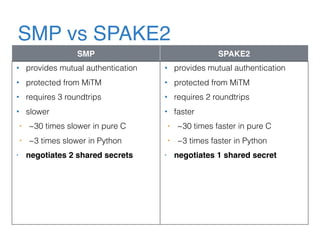
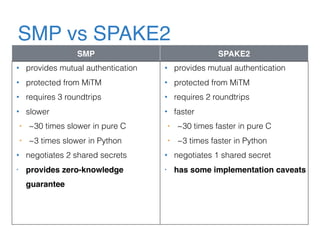
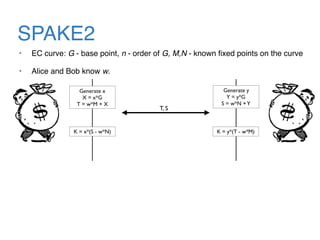
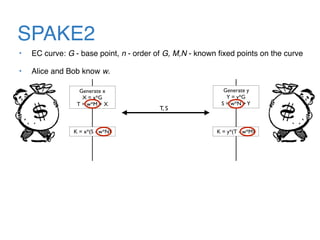
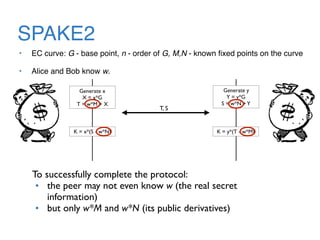
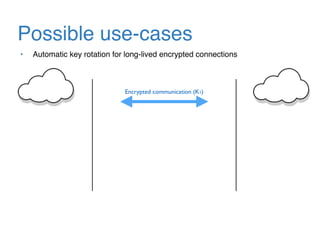
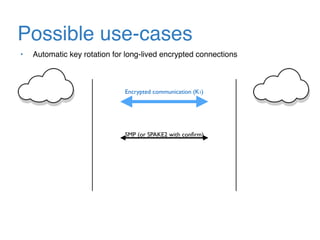
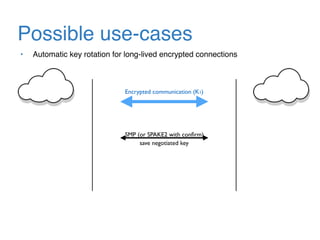
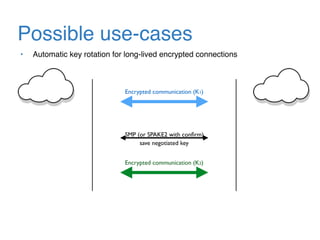
The document discusses the evolution of password authentication schemes, beginning with historical methods and moving to modern techniques such as HTTP Basic Authentication, Digest Authentication, OAuth, and password-authenticated key agreement protocols like SPAKE2. While several methods enhance security through hashing and encrypted communication, they remain vulnerable to various attacks, underscoring the need for high-entropy passwords and secure channels. It also compares the performance and security of different protocols, concluding that newer protocols offer better efficiency and security features.

Internet◦

Embed presentation

Download as PDF, PPTX
Overview and evolution of password- based authentication schemes Ignat Korchagin
Passwords in Roman Empire Ave, Caesar! http://ancienthistory.about.com/library/bl/bl_text_polybius6.htm • every night the watchword was changed • used a “roundtrip” delivery mechanism with confirmation to distribute the password
Passwords in modern world create password? “hunter2” hehe, no one will ever guess
HTTP basic authentication alice:example.com:hunter2
HTTP basic authentication alice:example.com:hunter2 • simple • password is sent in clear text • HTTPS is needed to protect from eavesdroppers • server DB leak compromises all the passwords
HTTP digest authentication • server stores Hash(alice:example.com:hunter2)
HTTP digest authentication • server stores Hash(alice:example.com:hunter2) GET secret info
HTTP digest authentication • server stores Hash(alice:example.com:hunter2) GET secret info nonce
HTTP digest authentication • server stores Hash(alice:example.com:hunter2) GET secret info nonce cnonce, Hash(Hash(alice:example.com:hunter2),nonce,cnonce)
HTTP digest authentication • passwords are not sent in clear text • protected from replay attacks • servers may store hashes of passwords instead of passwords themselves • server DB leak compromises passwords for specific realm only
HTTP digest authentication • passwords are not sent in clear text • protected from replay attacks • servers may store hashes of passwords instead of passwords themselves • server DB leak compromises passwords for specific realm only BUT…
HTTP digest authentication • still vulnerable to MiTM • still vulnerable to spoofed websites • requires HTTPS • vulnerable to dictionary attacks
HTTP digest authentication • still vulnerable to MiTM • still vulnerable to spoofed websites • requires HTTPS • vulnerable to dictionary attacks From RFC 7616: HTTP Digest Authentication, when used with human-memorable passwords, is vulnerable to dictionary attacks. Such attacks are much easier than cryptographic attacks on any widely used algorithm, including those that are no longer considered secure. In other words, algorithm agility does not make this usage any more secure. As a result, Digest Authentication SHOULD be used only with passwords that have a reasonable amount of entropy, e.g., 128-bit or more. Such passwords typically cannot be memorized by humans but can be used for automated web services. If Digest Authentication is being used, it SHOULD be over a secure channel like HTTPS.
HTTP OAuth auth token GET auth token
HTTP OAuth auth token GET auth token • allows delegations • does not need to use real credentials • needs other methods to authenticate on authorization server • HTTPS is needed to protect from eavesdroppers
HTTPS is hard
HTTPS is hard • problems with mixed content • maybe fixed with implementing proper content security policy
HTTPS is hard • problems with mixed content • maybe fixed with implementing proper content security policy • spoofed websites • similar domain names, same look and feel
HTTPS is hard • problems with mixed content • maybe fixed with implementing proper content security policy • spoofed websites • similar domain names, same look and feel • spoofed certificates • https://thehackerblog.com/keeping-positive-obtaining-arbitrary-wildcard-ssl- certificates-from-comodo-via-dangling-markup-injection/index.html
HTTPS is hard • problems with mixed content • maybe fixed with implementing proper content security policy • spoofed websites • similar domain names, same look and feel • spoofed certificates • https://thehackerblog.com/keeping-positive-obtaining-arbitrary-wildcard-ssl- certificates-from-comodo-via-dangling-markup-injection/index.html • compromised keys and certificates • certificate revocation is hard
Can we do better?
Socialist millionaires • Socialist millionaire problem is a way for two millionaires to check whether their wealth is equal
Socialist millionaires • EC curve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y.
Socialist millionaires • EC curve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y. Generate a2, a3, s G2a = a2*G G3a = a3*G Generate b2, b3, r G2b = b2*G G3b = b3*G G2a, G3a, G2b, G3b
Socialist millionaires • EC curve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y. Generate a2, a3, s G2a = a2*G G3a = a3*G Generate b2, b3, r G2b = b2*G G3b = b3*G G2 = a2*G2b G3 = a3*G3b Pa = s*G3 Qa = s*G + x*G2 G2 = b2*G2a G3 = b3*G3a Pb = r*G3 Qb = r*G + y*G2 G2a, G3a, G2b, G3b Pa, Qa, Pb, Qb
Socialist millionaires • EC curve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y. Generate a2, a3, s G2a = a2*G G3a = a3*G Generate b2, b3, r G2b = b2*G G3b = b3*G G2 = a2*G2b G3 = a3*G3b Pa = s*G3 Qa = s*G + x*G2 G2 = b2*G2a G3 = b3*G3a Pb = r*G3 Qb = r*G + y*G2 Ra = a3*(Qa-Qb) Rb = b3*(Qa-Qb) G2a, G3a, G2b, G3b Pa, Qa, Pb, Qb Ra, Rb
Socialist millionaires • EC curve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y. Generate a2, a3, s G2a = a2*G G3a = a3*G Generate b2, b3, r G2b = b2*G G3b = b3*G G2 = a2*G2b G3 = a3*G3b Pa = s*G3 Qa = s*G + x*G2 G2 = b2*G2a G3 = b3*G3a Pb = r*G3 Qb = r*G + y*G2 Ra = a3*(Qa-Qb) Rb = b3*(Qa-Qb) a3*Rb == Pa-Pb b3*Ra == Pa-Pb G2a, G3a, G2b, G3b Pa, Qa, Pb, Qb Ra, Rb
Socialist millionaires • EC curve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y. Generate a2, a3, s G2a = a2*G G3a = a3*G Generate b2, b3, r G2b = b2*G G3b = b3*G G2 = a2*G2b G3 = a3*G3b Pa = s*G3 Qa = s*G + x*G2 G2 = b2*G2a G3 = b3*G3a Pb = r*G3 Qb = r*G + y*G2 Ra = a3*(Qa-Qb) Rb = b3*(Qa-Qb) a3*Rb == Pa-Pb b3*Ra == Pa-Pb G2a, G3a, G2b, G3b Pa, Qa, Pb, Qb Ra, Rb a3 * Rb = b3 * Ra = (Pa - Pb) + (a3 * b3 * (x - y)) * G2
Socialist millionaires • EC curve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y. Generate a2, a3, s G2a = a2*G G3a = a3*G Generate b2, b3, r G2b = b2*G G3b = b3*G G2 = a2*G2b G3 = a3*G3b Pa = s*G3 Qa = s*G + x*G2 G2 = b2*G2a G3 = b3*G3a Pb = r*G3 Qb = r*G + y*G2 Ra = a3*(Qa-Qb) Rb = b3*(Qa-Qb) a3*Rb == Pa-Pb b3*Ra == Pa-Pb G2a, G3a, G2b, G3b Pa, Qa, Pb, Qb Ra, Rb a3 * Rb = b3 * Ra = (Pa - Pb) + (a3 * b3 * (x - y)) * G2
Socialist millionaires • Socialist millionaire problem is a way for two millionaires to check whether their wealth is equal • can be used to verify whether two parties posses the same secret • a passive attacker learns nothing about the protocol and its outcome • MiTM can do no better than passive attacker except disrupting the communication channel • even if one of the parties is dishonest, he learns nothing more that the protocol outcome • unlike most other zero-knowledge proofs requires O(1) protocol iterations • is adopted and has good history
OTR SMP • Uses 1536-bit group calculations
OTR SMP • Uses 1536-bit group calculations • BUT: LogJam!
OTR SMP • Uses 1536-bit group calculations • BUT: LogJam! • 512-bit broken • 1024-bit probably • 1536-bit is very close!
Themis SMP vs OTR SMP • Improving SMP • moved all cryptographic operations in ECC domain • modern (boring) cryptography (ed25519) • timing attacks protection • fast and performant • reduced memory footprint • support for many high-level languages • simple API • GitHub: https://github.com/cossacklabs/themis
SPAKE2 • EC curve: G - base point, n - order of G, M,N - known fixed points on the curve • Alice and Bob know w.
SPAKE2 • EC curve: G - base point, n - order of G, M,N - known fixed points on the curve • Alice and Bob know w. Generate x X = x*G T = w*M + X Generate y Y = y*G S = w*N +Y
SPAKE2 • EC curve: G - base point, n - order of G, M,N - known fixed points on the curve • Alice and Bob know w. Generate x X = x*G T = w*M + X Generate y Y = y*G S = w*N +Y T, S
SPAKE2 • EC curve: G - base point, n - order of G, M,N - known fixed points on the curve • Alice and Bob know w. Generate x X = x*G T = w*M + X Generate y Y = y*G S = w*N +Y K = x*(S - w*N) K = y*(T - w*M) T, S
SPAKE2 • PAKE - password-authenticated key agreement • basic SPAKE2 requires only 1 roundtrip • simple, requires small number of asymmetric cryptographic operations • easy to implement • provides a negotiated secret key as a protocol outcome
SPAKE2 • PAKE - password-authenticated key agreement • basic SPAKE2 requires only 1 roundtrip • simple, requires small number of asymmetric cryptographic operations • easy to implement • provides a negotiated secret key as a protocol outcome • Example: SPAKE2 (https://tools.ietf.org/html/draft-irtf- cfrg-spake2-03)
SMP vs SPAKE2 SMP SPAKE2 • provides mutual authentication • provides mutual authentication
SMP vs SPAKE2 SMP SPAKE2 • provides mutual authentication • protected from MiTM • provides mutual authentication • protected from MiTM
SMP vs SPAKE2 SMP SPAKE2 • provides mutual authentication • protected from MiTM • requires 3 roundtrips • provides mutual authentication • protected from MiTM • requires 2 roundtrips
Socialist millionaires • EC curve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y. Generate a2, a3, s G2a = a2*G G3a = a3*G Generate b2, b3, r G2b = b2*G G3b = b3*G G2 = a2*G2b G3 = a3*G3b Pa = s*G3 Qa = s*G + x*G2 G2 = b2*G2a G3 = b3*G3a Pb = r*G3 Qb = r*G + y*G2 Ra = a3*(Qa-Qb) Rb = b3*(Qa-Qb) a3*Rb == Pa-Pb b3*Ra == Pa-Pb G2a, G3a, G2b, G3b Pa, Qa, Pb, Qb Ra, Rb
SPAKE2 • EC curve: G - base point, n - order of G, M,N - known fixed points on the curve • Alice and Bob know w. Generate x X = x*G T = w*M + X Generate y Y = y*G S = w*N +Y K = x*(S - w*N) K = y*(T - w*M) T, S
SPAKE2 • EC curve: G - base point, n - order of G, M,N - known fixed points on the curve • Alice and Bob know w. Generate x X = x*G T = w*M + X Generate y Y = y*G S = w*N +Y K = x*(S - w*N) K = y*(T - w*M) T, S Key confirmation?
SMP vs SPAKE2 SMP SPAKE2 • provides mutual authentication • protected from MiTM • requires 3 roundtrips • slower • provides mutual authentication • protected from MiTM • requires 2 roundtrips • faster
SMP vs SPAKE2 SMP SPAKE2 • provides mutual authentication • protected from MiTM • requires 3 roundtrips • slower • ~30 times slower in pure C • provides mutual authentication • protected from MiTM • requires 2 roundtrips • faster • ~30 times faster in pure C
SMP vs SPAKE2 SMP SPAKE2 • provides mutual authentication • protected from MiTM • requires 3 roundtrips • slower • ~30 times slower in pure C • ~3 times slower in Python • provides mutual authentication • protected from MiTM • requires 2 roundtrips • faster • ~30 times faster in pure C • ~3 times faster in Python
SMP vs SPAKE2 SMP SPAKE2 • provides mutual authentication • protected from MiTM • requires 3 roundtrips • slower • ~30 times slower in pure C • ~3 times slower in Python • negotiates 2 shared secrets • provides mutual authentication • protected from MiTM • requires 2 roundtrips • faster • ~30 times faster in pure C • ~3 times faster in Python • negotiates 1 shared secret
Socialist millionaires • EC curve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y. Generate a2, a3, s G2a = a2*G G3a = a3*G Generate b2, b3, r G2b = b2*G G3b = b3*G G2 = a2*G2b G3 = a3*G3b Pa = s*G3 Qa = s*G + x*G2 G2 = b2*G2a G3 = b3*G3a Pb = r*G3 Qb = r*G + y*G2 Ra = a3*(Qa-Qb) Rb = b3*(Qa-Qb) a3*Rb == Pa-Pb b3*Ra == Pa-Pb G2a, G3a, G2b, G3b Pa, Qa, Pb, Qb Ra, Rb
Socialist millionaires • EC curve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y. Generate a2, a3, s G2a = a2*G G3a = a3*G Generate b2, b3, r G2b = b2*G G3b = b3*G G2 = a2*G2b G3 = a3*G3b Pa = s*G3 Qa = s*G + x*G2 G2 = b2*G2a G3 = b3*G3a Pb = r*G3 Qb = r*G + y*G2 Ra = a3*(Qa-Qb) Rb = b3*(Qa-Qb) a3*Rb == Pa-Pb b3*Ra == Pa-Pb G2a, G3a, G2b, G3b Pa, Qa, Pb, Qb Ra, Rb
SMP vs SPAKE2 SMP SPAKE2 • provides mutual authentication • protected from MiTM • requires 3 roundtrips • slower • ~30 times slower in pure C • ~3 times slower in Python • negotiates 2 shared secrets • provides zero-knowledge guarantee • provides mutual authentication • protected from MiTM • requires 2 roundtrips • faster • ~30 times faster in pure C • ~3 times faster in Python • negotiates 1 shared secret • has some implementation caveats
SPAKE2 • EC curve: G - base point, n - order of G, M,N - known fixed points on the curve • Alice and Bob know w. Generate x X = x*G T = w*M + X Generate y Y = y*G S = w*N +Y K = x*(S - w*N) K = y*(T - w*M) T, S
SPAKE2 • EC curve: G - base point, n - order of G, M,N - known fixed points on the curve • Alice and Bob know w. Generate x X = x*G T = w*M + X Generate y Y = y*G S = w*N +Y K = x*(S - w*N) K = y*(T - w*M) T, S
SPAKE2 • EC curve: G - base point, n - order of G, M,N - known fixed points on the curve • Alice and Bob know w. Generate x X = x*G T = w*M + X Generate y Y = y*G S = w*N +Y K = x*(S - w*N) K = y*(T - w*M) T, S To successfully complete the protocol: • the peer may not even know w (the real secret information) • but only w*M and w*N (its public derivatives)
Possible use-cases
Possible use-cases
Possible use-cases Encrypted communication (K1) • Automatic key rotation for long-lived encrypted connections
Possible use-cases SMP (or SPAKE2 with confirm) Encrypted communication (K1) • Automatic key rotation for long-lived encrypted connections
Possible use-cases SMP (or SPAKE2 with confirm) Encrypted communication (K1) • Automatic key rotation for long-lived encrypted connections save negotiated key
Possible use-cases SMP (or SPAKE2 with confirm) Encrypted communication (K1) Encrypted communication (K2) • Automatic key rotation for long-lived encrypted connections save negotiated key
Conclusions • Zero-knowledge protocols are useful building blocks for enhanced security and privacy preserving protocols • They can be useful in a scenario where one of the protocol participants may be malicious • You may use SPAKE2 for many real world tasks, but you have to be aware of the caveats • Socialist millionaire protocol provides more security guarantees, although with some performance penalty
Links • Paper: https://www.cossacklabs.com/files/secure- comparator-paper-rev12.pdf • SMP code: https://github.com/cossacklabs/themis • SPAKE2 code: https://boringssl.googlesource.com/ boringssl/+/master/crypto/curve25519/spake25519.c • sctest.c: https://gist.github.com/secumod/ d3a064ee93e3eda74aebd379e60ede66 • spake2test.c: https://gist.github.com/secumod/ 5c35c067a4e25fbe038f09a2706b236b
Thank you! Questions?

More Related Content

PPTX
Cyber security
bySiblu28
 
PPTX
Cyber crime and security ppt
byLipsita Behera
 
PDF
Apache Commons ソースリーディングの会：Codec
bymoai kids
 
ODP
From 0 to 60 in SPARQL in 50 Minutes
byewg118
 
PPTX
Cyber-crime PPT
byAnshuman Tripathi
 
PPTX
Cyber crime ppt
byMOE515253
 
PPTX
Enforcing Web security and privacy with zero-knowledge protocols
byIgnat Korchagin
 
PPTX
Demystifying Zero Knowledge Proofs [FINAL].pptx
byRedWhite12
 
Cyber security
bySiblu28
 
Cyber crime and security ppt
byLipsita Behera
 
Apache Commons ソースリーディングの会：Codec
bymoai kids
 
From 0 to 60 in SPARQL in 50 Minutes
byewg118
 
Cyber-crime PPT
byAnshuman Tripathi
 
Cyber crime ppt
byMOE515253
 
Enforcing Web security and privacy with zero-knowledge protocols
byIgnat Korchagin
 
Demystifying Zero Knowledge Proofs [FINAL].pptx
byRedWhite12
 

Similar to Overview and evolution of password-based authentication schemes

PDF
CNIT 141 12. Elliptic Curves
bySam Bowne
 
PDF
Elliptic Curve Cryptography for those who are afraid of maths
byMartijn Grooten
 
PDF
CNIT 141 12. Elliptic Curves
bySam Bowne
 
PDF
CNIT 141: 12. Elliptic Curves
bySam Bowne
 
PDF
CNIT 141 12. Elliptic Curves
bySam Bowne
 
PDF
12 Elliptic Curves
bySam Bowne
 
PDF
Module 3_ECC.part_2 Cryptography Elliptic curve cryptography.pdf
byrintucs
 
PDF
Report
byConor McMenamin
 
PPT
Elliptic Curve Digital Signature Algorithm (ECDSA).ppt
bytipurple7989
 
PDF
Ecc cipher processor based on knapsack algorithm
byAlexander Decker
 
PDF
MAPREDUCE METHODOLOGY FOR ELLIPTICAL CURVE DISCRETE LOGARITHMIC PROBLEMS – SE...
byIAEME Publication
 
PDF
Efficient ECC encryption for WSN’s
byIDES Editor
 
DOCX
Assignment 2 (1) (1).docx
bypinstechwork
 
PDF
Elliptic Curves in Cryptography
byCSNP
 
PDF
Ibe weil pairing
bysravanbabu
 
PDF
Low Power FPGA Based Elliptical Curve Cryptography
byIOSR Journals
 
PDF
Low Power FPGA Based Elliptical Curve Cryptography
byIOSR Journals
 
PDF
AllBits presentation - Security in Theory
byAllBits BVBA (freelancer)
 
PPTX
2.13 Inroductory idea of elliptic curve cryptography.pptx
bygirilogu2
 
PPTX
abhijith_dushyant_EllipticCurveCryptography.pptx
bytahircs1
 
CNIT 141 12. Elliptic Curves
bySam Bowne
 
Elliptic Curve Cryptography for those who are afraid of maths
byMartijn Grooten
 
CNIT 141 12. Elliptic Curves
bySam Bowne
 
CNIT 141: 12. Elliptic Curves
bySam Bowne
 
CNIT 141 12. Elliptic Curves
bySam Bowne
 
12 Elliptic Curves
bySam Bowne
 
Module 3_ECC.part_2 Cryptography Elliptic curve cryptography.pdf
byrintucs
 
Report
byConor McMenamin
 
Elliptic Curve Digital Signature Algorithm (ECDSA).ppt
bytipurple7989
 
Ecc cipher processor based on knapsack algorithm
byAlexander Decker
 
MAPREDUCE METHODOLOGY FOR ELLIPTICAL CURVE DISCRETE LOGARITHMIC PROBLEMS – SE...
byIAEME Publication
 
Efficient ECC encryption for WSN’s
byIDES Editor
 
Assignment 2 (1) (1).docx
bypinstechwork
 
Elliptic Curves in Cryptography
byCSNP
 
Ibe weil pairing
bysravanbabu
 
Low Power FPGA Based Elliptical Curve Cryptography
byIOSR Journals
 
Low Power FPGA Based Elliptical Curve Cryptography
byIOSR Journals
 
AllBits presentation - Security in Theory
byAllBits BVBA (freelancer)
 
2.13 Inroductory idea of elliptic curve cryptography.pptx
bygirilogu2
 
abhijith_dushyant_EllipticCurveCryptography.pptx
bytahircs1
 

Recently uploaded

PDF
Top 3 Snapchat Monitoring Apps of 2026 for Activity Tracking
byMichael Carter
 
PPTX
Your Complete Brand Protection Guide with Fieldwatch.ai!
byFieldwatch ai
 
PPTX
Living in IT Era Module 5 - (DIGITAL TECHNOLOGY AND SOCIAL CHANGES).pptx
bycjregua03
 
PDF
Weaponizing the Neutral Web: Analyzing Adversary Botnets for Offensive Cyber ...
byJoe Slowik
 
PDF
The Girl Who Left a Mark - Deep Impact of Kindness to a person
byAnoop Singh Nagi
 
PPTX
AWS Architecture Design Icons Template.pptx
bybiqtor1
 
Top 3 Snapchat Monitoring Apps of 2026 for Activity Tracking
byMichael Carter
 
Your Complete Brand Protection Guide with Fieldwatch.ai!
byFieldwatch ai
 
Living in IT Era Module 5 - (DIGITAL TECHNOLOGY AND SOCIAL CHANGES).pptx
bycjregua03
 
Weaponizing the Neutral Web: Analyzing Adversary Botnets for Offensive Cyber ...
byJoe Slowik
 
The Girl Who Left a Mark - Deep Impact of Kindness to a person
byAnoop Singh Nagi
 
AWS Architecture Design Icons Template.pptx
bybiqtor1
 

Overview and evolution of password-based authentication schemes

  • 1.
    Overview and evolutionof password- based authentication schemes Ignat Korchagin
  • 2.
    Passwords in RomanEmpire Ave, Caesar! http://ancienthistory.about.com/library/bl/bl_text_polybius6.htm • every night the watchword was changed • used a “roundtrip” delivery mechanism with confirmation to distribute the password
  • 3.
    Passwords in modernworld create password? “hunter2” hehe, no one will ever guess
  • 4.
  • 5.
    HTTP basic authentication alice:example.com:hunter2 •simple • password is sent in clear text • HTTPS is needed to protect from eavesdroppers • server DB leak compromises all the passwords
  • 6.
    HTTP digest authentication •server stores Hash(alice:example.com:hunter2)
  • 7.
    HTTP digest authentication •server stores Hash(alice:example.com:hunter2) GET secret info
  • 8.
    HTTP digest authentication •server stores Hash(alice:example.com:hunter2) GET secret info nonce
  • 9.
    HTTP digest authentication •server stores Hash(alice:example.com:hunter2) GET secret info nonce cnonce, Hash(Hash(alice:example.com:hunter2),nonce,cnonce)
  • 10.
    HTTP digest authentication •passwords are not sent in clear text • protected from replay attacks • servers may store hashes of passwords instead of passwords themselves • server DB leak compromises passwords for specific realm only
  • 11.
    HTTP digest authentication •passwords are not sent in clear text • protected from replay attacks • servers may store hashes of passwords instead of passwords themselves • server DB leak compromises passwords for specific realm only BUT…
  • 12.
    HTTP digest authentication •still vulnerable to MiTM • still vulnerable to spoofed websites • requires HTTPS • vulnerable to dictionary attacks
  • 13.
    HTTP digest authentication •still vulnerable to MiTM • still vulnerable to spoofed websites • requires HTTPS • vulnerable to dictionary attacks From RFC 7616: HTTP Digest Authentication, when used with human-memorable passwords, is vulnerable to dictionary attacks. Such attacks are much easier than cryptographic attacks on any widely used algorithm, including those that are no longer considered secure. In other words, algorithm agility does not make this usage any more secure. As a result, Digest Authentication SHOULD be used only with passwords that have a reasonable amount of entropy, e.g., 128-bit or more. Such passwords typically cannot be memorized by humans but can be used for automated web services. If Digest Authentication is being used, it SHOULD be over a secure channel like HTTPS.
  • 14.
  • 15.
    HTTP OAuth auth token GET authtoken • allows delegations • does not need to use real credentials • needs other methods to authenticate on authorization server • HTTPS is needed to protect from eavesdroppers
  • 16.
  • 17.
    HTTPS is hard •problems with mixed content • maybe fixed with implementing proper content security policy
  • 18.
    HTTPS is hard •problems with mixed content • maybe fixed with implementing proper content security policy • spoofed websites • similar domain names, same look and feel
  • 19.
    HTTPS is hard •problems with mixed content • maybe fixed with implementing proper content security policy • spoofed websites • similar domain names, same look and feel • spoofed certificates • https://thehackerblog.com/keeping-positive-obtaining-arbitrary-wildcard-ssl- certificates-from-comodo-via-dangling-markup-injection/index.html
  • 20.
    HTTPS is hard •problems with mixed content • maybe fixed with implementing proper content security policy • spoofed websites • similar domain names, same look and feel • spoofed certificates • https://thehackerblog.com/keeping-positive-obtaining-arbitrary-wildcard-ssl- certificates-from-comodo-via-dangling-markup-injection/index.html • compromised keys and certificates • certificate revocation is hard
  • 21.
    Can we dobetter?
  • 22.
    Socialist millionaires • Socialistmillionaire problem is a way for two millionaires to check whether their wealth is equal
  • 23.
    Socialist millionaires • ECcurve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y.
  • 24.
    Socialist millionaires • ECcurve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y. Generate a2, a3, s G2a = a2*G G3a = a3*G Generate b2, b3, r G2b = b2*G G3b = b3*G G2a, G3a, G2b, G3b
  • 25.
    Socialist millionaires • ECcurve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y. Generate a2, a3, s G2a = a2*G G3a = a3*G Generate b2, b3, r G2b = b2*G G3b = b3*G G2 = a2*G2b G3 = a3*G3b Pa = s*G3 Qa = s*G + x*G2 G2 = b2*G2a G3 = b3*G3a Pb = r*G3 Qb = r*G + y*G2 G2a, G3a, G2b, G3b Pa, Qa, Pb, Qb
  • 26.
    Socialist millionaires • ECcurve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y. Generate a2, a3, s G2a = a2*G G3a = a3*G Generate b2, b3, r G2b = b2*G G3b = b3*G G2 = a2*G2b G3 = a3*G3b Pa = s*G3 Qa = s*G + x*G2 G2 = b2*G2a G3 = b3*G3a Pb = r*G3 Qb = r*G + y*G2 Ra = a3*(Qa-Qb) Rb = b3*(Qa-Qb) G2a, G3a, G2b, G3b Pa, Qa, Pb, Qb Ra, Rb
  • 27.
    Socialist millionaires • ECcurve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y. Generate a2, a3, s G2a = a2*G G3a = a3*G Generate b2, b3, r G2b = b2*G G3b = b3*G G2 = a2*G2b G3 = a3*G3b Pa = s*G3 Qa = s*G + x*G2 G2 = b2*G2a G3 = b3*G3a Pb = r*G3 Qb = r*G + y*G2 Ra = a3*(Qa-Qb) Rb = b3*(Qa-Qb) a3*Rb == Pa-Pb b3*Ra == Pa-Pb G2a, G3a, G2b, G3b Pa, Qa, Pb, Qb Ra, Rb
  • 28.
    Socialist millionaires • ECcurve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y. Generate a2, a3, s G2a = a2*G G3a = a3*G Generate b2, b3, r G2b = b2*G G3b = b3*G G2 = a2*G2b G3 = a3*G3b Pa = s*G3 Qa = s*G + x*G2 G2 = b2*G2a G3 = b3*G3a Pb = r*G3 Qb = r*G + y*G2 Ra = a3*(Qa-Qb) Rb = b3*(Qa-Qb) a3*Rb == Pa-Pb b3*Ra == Pa-Pb G2a, G3a, G2b, G3b Pa, Qa, Pb, Qb Ra, Rb a3 * Rb = b3 * Ra = (Pa - Pb) + (a3 * b3 * (x - y)) * G2
  • 29.
    Socialist millionaires • ECcurve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y. Generate a2, a3, s G2a = a2*G G3a = a3*G Generate b2, b3, r G2b = b2*G G3b = b3*G G2 = a2*G2b G3 = a3*G3b Pa = s*G3 Qa = s*G + x*G2 G2 = b2*G2a G3 = b3*G3a Pb = r*G3 Qb = r*G + y*G2 Ra = a3*(Qa-Qb) Rb = b3*(Qa-Qb) a3*Rb == Pa-Pb b3*Ra == Pa-Pb G2a, G3a, G2b, G3b Pa, Qa, Pb, Qb Ra, Rb a3 * Rb = b3 * Ra = (Pa - Pb) + (a3 * b3 * (x - y)) * G2
  • 30.
    Socialist millionaires • Socialistmillionaire problem is a way for two millionaires to check whether their wealth is equal • can be used to verify whether two parties posses the same secret • a passive attacker learns nothing about the protocol and its outcome • MiTM can do no better than passive attacker except disrupting the communication channel • even if one of the parties is dishonest, he learns nothing more that the protocol outcome • unlike most other zero-knowledge proofs requires O(1) protocol iterations • is adopted and has good history
  • 31.
    OTR SMP • Uses1536-bit group calculations
  • 32.
    OTR SMP • Uses1536-bit group calculations • BUT: LogJam!
  • 33.
    OTR SMP • Uses1536-bit group calculations • BUT: LogJam! • 512-bit broken • 1024-bit probably • 1536-bit is very close!
  • 34.
    Themis SMP vsOTR SMP • Improving SMP • moved all cryptographic operations in ECC domain • modern (boring) cryptography (ed25519) • timing attacks protection • fast and performant • reduced memory footprint • support for many high-level languages • simple API • GitHub: https://github.com/cossacklabs/themis
  • 35.
    SPAKE2 • EC curve:G - base point, n - order of G, M,N - known fixed points on the curve • Alice and Bob know w.
  • 36.
    SPAKE2 • EC curve:G - base point, n - order of G, M,N - known fixed points on the curve • Alice and Bob know w. Generate x X = x*G T = w*M + X Generate y Y = y*G S = w*N +Y
  • 37.
    SPAKE2 • EC curve:G - base point, n - order of G, M,N - known fixed points on the curve • Alice and Bob know w. Generate x X = x*G T = w*M + X Generate y Y = y*G S = w*N +Y T, S
  • 38.
    SPAKE2 • EC curve:G - base point, n - order of G, M,N - known fixed points on the curve • Alice and Bob know w. Generate x X = x*G T = w*M + X Generate y Y = y*G S = w*N +Y K = x*(S - w*N) K = y*(T - w*M) T, S
  • 39.
    SPAKE2 • PAKE -password-authenticated key agreement • basic SPAKE2 requires only 1 roundtrip • simple, requires small number of asymmetric cryptographic operations • easy to implement • provides a negotiated secret key as a protocol outcome
  • 40.
    SPAKE2 • PAKE -password-authenticated key agreement • basic SPAKE2 requires only 1 roundtrip • simple, requires small number of asymmetric cryptographic operations • easy to implement • provides a negotiated secret key as a protocol outcome • Example: SPAKE2 (https://tools.ietf.org/html/draft-irtf- cfrg-spake2-03)
  • 41.
    SMP vs SPAKE2 SMPSPAKE2 • provides mutual authentication • provides mutual authentication
  • 42.
    SMP vs SPAKE2 SMPSPAKE2 • provides mutual authentication • protected from MiTM • provides mutual authentication • protected from MiTM
  • 43.
    SMP vs SPAKE2 SMPSPAKE2 • provides mutual authentication • protected from MiTM • requires 3 roundtrips • provides mutual authentication • protected from MiTM • requires 2 roundtrips
  • 44.
    Socialist millionaires • ECcurve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y. Generate a2, a3, s G2a = a2*G G3a = a3*G Generate b2, b3, r G2b = b2*G G3b = b3*G G2 = a2*G2b G3 = a3*G3b Pa = s*G3 Qa = s*G + x*G2 G2 = b2*G2a G3 = b3*G3a Pb = r*G3 Qb = r*G + y*G2 Ra = a3*(Qa-Qb) Rb = b3*(Qa-Qb) a3*Rb == Pa-Pb b3*Ra == Pa-Pb G2a, G3a, G2b, G3b Pa, Qa, Pb, Qb Ra, Rb
  • 45.
    SPAKE2 • EC curve:G - base point, n - order of G, M,N - known fixed points on the curve • Alice and Bob know w. Generate x X = x*G T = w*M + X Generate y Y = y*G S = w*N +Y K = x*(S - w*N) K = y*(T - w*M) T, S
  • 46.
    SPAKE2 • EC curve:G - base point, n - order of G, M,N - known fixed points on the curve • Alice and Bob know w. Generate x X = x*G T = w*M + X Generate y Y = y*G S = w*N +Y K = x*(S - w*N) K = y*(T - w*M) T, S Key confirmation?
  • 47.
    SMP vs SPAKE2 SMPSPAKE2 • provides mutual authentication • protected from MiTM • requires 3 roundtrips • slower • provides mutual authentication • protected from MiTM • requires 2 roundtrips • faster
  • 48.
    SMP vs SPAKE2 SMPSPAKE2 • provides mutual authentication • protected from MiTM • requires 3 roundtrips • slower • ~30 times slower in pure C • provides mutual authentication • protected from MiTM • requires 2 roundtrips • faster • ~30 times faster in pure C
  • 49.
    SMP vs SPAKE2 SMPSPAKE2 • provides mutual authentication • protected from MiTM • requires 3 roundtrips • slower • ~30 times slower in pure C • ~3 times slower in Python • provides mutual authentication • protected from MiTM • requires 2 roundtrips • faster • ~30 times faster in pure C • ~3 times faster in Python
  • 50.
    SMP vs SPAKE2 SMPSPAKE2 • provides mutual authentication • protected from MiTM • requires 3 roundtrips • slower • ~30 times slower in pure C • ~3 times slower in Python • negotiates 2 shared secrets • provides mutual authentication • protected from MiTM • requires 2 roundtrips • faster • ~30 times faster in pure C • ~3 times faster in Python • negotiates 1 shared secret
  • 51.
    Socialist millionaires • ECcurve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y. Generate a2, a3, s G2a = a2*G G3a = a3*G Generate b2, b3, r G2b = b2*G G3b = b3*G G2 = a2*G2b G3 = a3*G3b Pa = s*G3 Qa = s*G + x*G2 G2 = b2*G2a G3 = b3*G3a Pb = r*G3 Qb = r*G + y*G2 Ra = a3*(Qa-Qb) Rb = b3*(Qa-Qb) a3*Rb == Pa-Pb b3*Ra == Pa-Pb G2a, G3a, G2b, G3b Pa, Qa, Pb, Qb Ra, Rb
  • 52.
    Socialist millionaires • ECcurve: G - base point, n - order of G • Alice and Bob have x and y respectively. Both want to know whether x==y. Generate a2, a3, s G2a = a2*G G3a = a3*G Generate b2, b3, r G2b = b2*G G3b = b3*G G2 = a2*G2b G3 = a3*G3b Pa = s*G3 Qa = s*G + x*G2 G2 = b2*G2a G3 = b3*G3a Pb = r*G3 Qb = r*G + y*G2 Ra = a3*(Qa-Qb) Rb = b3*(Qa-Qb) a3*Rb == Pa-Pb b3*Ra == Pa-Pb G2a, G3a, G2b, G3b Pa, Qa, Pb, Qb Ra, Rb
  • 53.
    SMP vs SPAKE2 SMPSPAKE2 • provides mutual authentication • protected from MiTM • requires 3 roundtrips • slower • ~30 times slower in pure C • ~3 times slower in Python • negotiates 2 shared secrets • provides zero-knowledge guarantee • provides mutual authentication • protected from MiTM • requires 2 roundtrips • faster • ~30 times faster in pure C • ~3 times faster in Python • negotiates 1 shared secret • has some implementation caveats
  • 54.
    SPAKE2 • EC curve:G - base point, n - order of G, M,N - known fixed points on the curve • Alice and Bob know w. Generate x X = x*G T = w*M + X Generate y Y = y*G S = w*N +Y K = x*(S - w*N) K = y*(T - w*M) T, S
  • 55.
    SPAKE2 • EC curve:G - base point, n - order of G, M,N - known fixed points on the curve • Alice and Bob know w. Generate x X = x*G T = w*M + X Generate y Y = y*G S = w*N +Y K = x*(S - w*N) K = y*(T - w*M) T, S
  • 56.
    SPAKE2 • EC curve:G - base point, n - order of G, M,N - known fixed points on the curve • Alice and Bob know w. Generate x X = x*G T = w*M + X Generate y Y = y*G S = w*N +Y K = x*(S - w*N) K = y*(T - w*M) T, S To successfully complete the protocol: • the peer may not even know w (the real secret information) • but only w*M and w*N (its public derivatives)
  • 57.
  • 58.
  • 59.
    Possible use-cases Encrypted communication(K1) • Automatic key rotation for long-lived encrypted connections
  • 60.
    Possible use-cases SMP (orSPAKE2 with confirm) Encrypted communication (K1) • Automatic key rotation for long-lived encrypted connections
  • 61.
    Possible use-cases SMP (orSPAKE2 with confirm) Encrypted communication (K1) • Automatic key rotation for long-lived encrypted connections save negotiated key
  • 62.
    Possible use-cases SMP (orSPAKE2 with confirm) Encrypted communication (K1) Encrypted communication (K2) • Automatic key rotation for long-lived encrypted connections save negotiated key
  • 63.
    Conclusions • Zero-knowledge protocolsare useful building blocks for enhanced security and privacy preserving protocols • They can be useful in a scenario where one of the protocol participants may be malicious • You may use SPAKE2 for many real world tasks, but you have to be aware of the caveats • Socialist millionaire protocol provides more security guarantees, although with some performance penalty
  • 64.
    Links • Paper: https://www.cossacklabs.com/files/secure- comparator-paper-rev12.pdf •SMP code: https://github.com/cossacklabs/themis • SPAKE2 code: https://boringssl.googlesource.com/ boringssl/+/master/crypto/curve25519/spake25519.c • sctest.c: https://gist.github.com/secumod/ d3a064ee93e3eda74aebd379e60ede66 • spake2test.c: https://gist.github.com/secumod/ 5c35c067a4e25fbe038f09a2706b236b
  • 65.