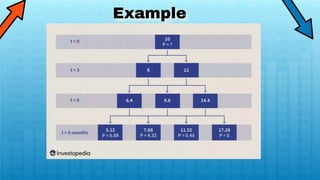
Option pricing models use mathematical formulas to calculate the theoretical value of an option based on variables like volatility, stock price, strike price, time to expiration, and risk-free interest rates. The most common models are the Black-Scholes model for European options and the binomial model. Both make assumptions like constant interest rates and that stock prices follow random walks. The models provide estimates of an option's fair value to help investors evaluate prices and make informed trading decisions.

1. Option Pricing Models

2. What are option pricing
models?
 Option pricing models are mathematical models that use certain
variables to calculate the theoretical value of an option. The
theoretical value of an option is an estimate of what an option should
be worth using all known inputs.
 In other words, option pricing models provide us a fair value of an
option.
 There are several option pricing models such as the Black-Scholes
Model (BSM), binomial option pricing, and Monte-Carlo simulation.

3. Assumptions
Constant risk-free interest
rates and no Dividends.
No transaction costs
Random walk: meaning
that the price can go up or
down with the same
probability at any given
moment in time
Normal distribution
of returns.
Black-Scholes Model
European options: which
means that it can only be
exercised at the expiration
date

4. Model
Helps calculate the theoretical value for a call or a
put option based on five variables viz Volatility,
Underlying stock price, Strike price, Time, and
Risk-free rate.
In mathematical notation:

5. • Black-Scholes assumes stock prices follow
a lognormal distribution because asset
prices cannot be negative (they are
bounded by zero).
• Often, asset prices are observed to have
significant right skewness and some
degree of kurtosis (fat tails). This means
high-risk downward moves often happen
more often in the market than a normal
distribution predicts.

7. Binomial Option Pricing Model
• Binomial option pricing is a mathematical model used to
determine the fair price or theoretical value for a call or a put
option based on the assumption of a binomial distribution of
stock prices.
• The model is a discrete-time model that traces the evolution of
the option's key underlying variables in discrete-time by means
of a binomial lattice or tree.
• The binomial model is a relatively simple model that is used to
price options and is mathematically simple and easy to use
when compared to other complex models such as the Black-
Scholes model.

8. Assumptions
The risk-free rate
remains constant
The market is
frictionless, and there
are no transaction
costs and no taxes
The underlying asset
pays no dividends
Investors are risk-
neutral, indifferent to
risk

9. Mathematically,

10. Example

11. Comparison
• The model assumes that stock price movement follows a
random walk, which is consistent with the Black-Scholes
model.
• The binomial model is more accurate than the Black-Scholes
model for longer-dated options on securities with dividend
payments.

12. Conclusion
Plays crucial role in
quantifying and
effectively managing
the risk linked
to options.
Determines whether a
particular contract is
overpriced or
underpriced relative to
its intrinsic value. This
information can be
used to make
informed trading
decisions.
Enables investors to
assess the fair value
of options and make
informed investment
decisions.
Gives insights into the
responsiveness of option
prices to alterations in factors
like the price of the
underlying asset, volatility,
and expiration period. Aids
investors in evaluating and
mitigating their vulnerability
to market fluctuations and
potential financial setbacks.

13. Thank you!