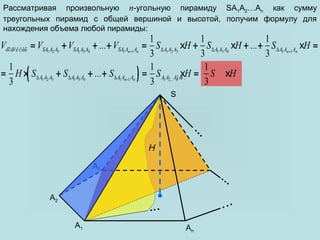
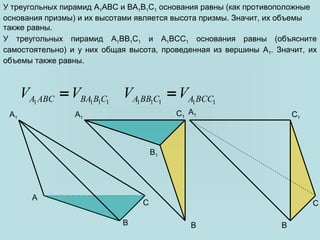
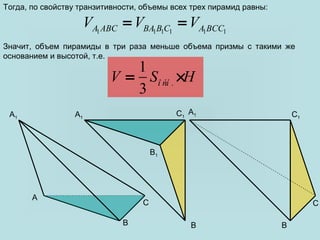
Документ посвящен вычислению объема пирамиды, включая треугольные и n-угольные пирамиды. Объем пирамиды определяется как одна треть произведения площади основания на высоту. Также рассматриваются методы доказательства равенства объемов различных пирамид, основанных на свойствах подобных фигур и сечений.

1. Объём пирамидыОбъём пирамиды.
Геометрия,Геометрия,
11 класс11 класс..
Воробьев Леонид Альбертович,Воробьев Леонид Альбертович,
1
3
ï èðàì èäû î ñí .V S H= ×

2. Рассмотрим произвольную треугольную пирамиду SABC с высотой SO=H.
A
B
C
S
O
H
O1
h
2
2
î ńí .
ńĺ ÷.
S H
S h
=
2
2
î ńí .
ńĺ ÷.
S h
S
H
×
=
Построим сечение пирамиды, параллельное плоскости основания и находящееся
на расстоянии h от её вершины.
Т.к. ∆ABCA1B1C1, то по свойству площадей подобных фигур :
A1
C1
B1
h ∈[0; H ]
⇒
Т.к. h – изменяющаяся
величина, то площадь
сечения можно
рассматривать как
функцию от переменной h,
где h – расстояние от
вершины пирамиды до
плоскости основания.

3. h
H
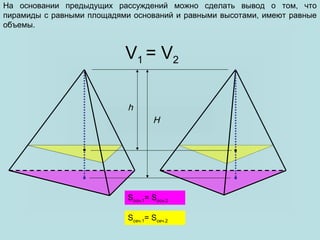
Используя понятие бесконечной интегральной суммы, объем данной пирамиды
можно получить как бесконечную сумму площадей таких сечений, построенных
вдоль высоты.
h ∈[0; H ]

4. На основании предыдущих рассуждений можно сделать вывод о том, что
пирамиды с равными площадями оснований и равными высотами, имеют равные
объемы.
H
Sосн.1= Sосн.2
V1 = V2
h
Sсеч.1= Sсеч.2

5. A
B
C
B1
A1 C1
C
A1
B
Рассмотрим произвольную треугольную призму ABCA1B1C1.
1) Разобьем её на две части секущей плоскостью (A1BC).
2) Получились две пространственные фигуры: треугольная пирамида A1ABC и
четырехугольная пирамида A1BCC1B1 (обе пирамиды с вершиной A1).

6. A C
B1
A1 C1
C
A1
B B
Теперь разобьём четырёхугольную пирамиду A1BCC1B1 секущей плоскостью
(A1C1B) на две треугольные пирамиды: A1BB1C1 и A1BCC1 (обе пирамиды с
вершиной A1).
A1 C1
B

7. A
C
B1
A1C1
C
A1
B B
A1 C1
B
У треугольных пирамид A1ABC и BA1B1C1 основания равны (как противоположные
основания призмы) и их высотами является высота призмы. Значит, их объемы
также равны.
У треугольных пирамид A1BB1C1 и A1BCC1 основания равны (объясните
самостоятельно) и у них общая высота, проведенная из вершины A1. Значит, их
объемы также равны.
1 1 1 1A ABC BA B CV V= 1 1 1 1 1A BB C A BCCV V=

8. A
C
B1
A1C1
C
A1
B B
A1 C1
B
1 1 1 1 1 1A ABC BA B C A BCCV V V= =
Тогда, по свойству транзитивности, объемы всех трех пирамид равны:
Значит, объем пирамиды в три раза меньше объема призмы с такими же
основанием и высотой, т.е.
1
3
î ńí .V S H= ×

9. 2 3
2
2 2 2
0 0 0
1
03 3
H H H
î ńí . î ńí . î ńí .
ńĺ ÷. î ńí .
HS h S S h
V S dh dh h dh S H
H H H
×
= = = = = ×∫ ∫ ∫
h
H
h
Эту же формулу можно было получить непосредственным интегрированием
площади сечения, как функции, зависящей от расстояния h:
h ∈[0; H ]
0

10. Рассматривая произвольную n-угольную пирамиду SA1A2…An как сумму
треугольных пирамид с общей вершиной и высотой, получим формулу для
нахождения объема любой пирамиды:
S
A3
An
A2
A1
H
( )
1 2 3 1 3 4 1 1 1 2 3 1 3 4 1 1
1 2 3 1 3 4 1 1 1 2
1 1 1
3 3 3
1 1 1
3 3 3
n n n n
n n ... n
ďčđŕě čäű SA A A SA A A SA A A A A A A A A A A A
A A A A A A A A A A A Aî ńí .
V V V ... V S H S H ... S H
H S S ... S S H S H
∆ ∆ ∆
∆ ∆ ∆
− −
−
= + + + = × + × + + × =
= × + + + = × = ×

11. Итак, для любой n-угольной пирамиды:
1
3
ďčđŕě čäű î ńí .V S H= ×
,где Sосн. – площадь основания пирамиды, H – высота пирамиды.