The document discusses machine learning concepts focused on linear models for classification, covering topics such as decision theory, classification models, logistic regression, and multi-class classification strategies. It explains various types of classifiers including generative and discriminative models, as well as practical applications in text and image classification. Additionally, it addresses challenges like overfitting, underfitting, and the importance of regularization.



![BITS Pilani, Pilani Campus
Inductive Learning Hypothesis :Interpretation
• Target Concept : t
• Discrete : f(x) ∈ {Yes, No, Maybe}
• Continuous : f(x) ∈ [20-100]
• Probability Estimation : f(x) ∈ [0-1]
5
Classification
Regression](https://image.slidesharecdn.com/module4-linearmodelforclassification-240318104502-7393e1b2/85/Module-4-Linear-Model-for-Classification-pptx-4-320.jpg)
![BITS Pilani, Pilani Campus
Decision Theory
• Target Concept : t
• Discrete : f(x) ∈ {Yes, No} ie., t ∈ {0, 1}
• Continuous : f(x) ∈ [20-100]
• Probability Estimation : f(x) ∈ [0-1]
6
Binary Classification](https://image.slidesharecdn.com/module4-linearmodelforclassification-240318104502-7393e1b2/85/Module-4-Linear-Model-for-Classification-pptx-5-320.jpg)
![BITS Pilani, Pilani Campus
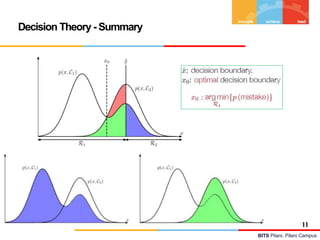
Decision Theory :
The decision problem: given x, predict t according to a probabilistic model p(x, t)
• Target Concept : t
• Discrete : f(x) ∈ {Yes, No} ie., t ∈ {0, 1}
• Continuous : f(x) ∈ [20-100]
• Probability Estimation : f(x) ∈ [0-1]
7
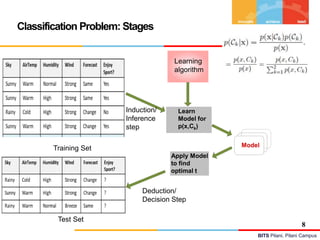
X =< , , , , , > = P(Ck| X)
p(x, Ck ) is the (central!) inference problem](https://image.slidesharecdn.com/module4-linearmodelforclassification-240318104502-7393e1b2/85/Module-4-Linear-Model-for-Classification-pptx-6-320.jpg)

![BITS Pilani, Pilani Campus
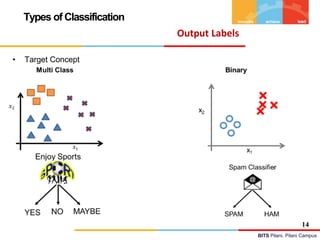
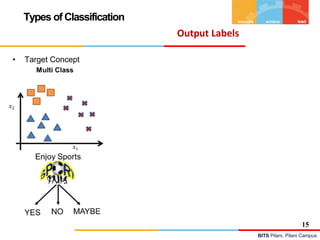
Types of Classification
Inductive Learning Hypothesis :Interpretation
• Target Concept
• Discrete : f(x) ∈ {Yes, No, Maybe}
• Continuous : f(x) ∈ [20-100]
• Probability Estimation : f(x) ∈ [0-1]
13
Classification
Regression](https://image.slidesharecdn.com/module4-linearmodelforclassification-240318104502-7393e1b2/85/Module-4-Linear-Model-for-Classification-pptx-12-320.jpg)



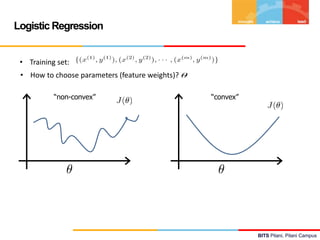
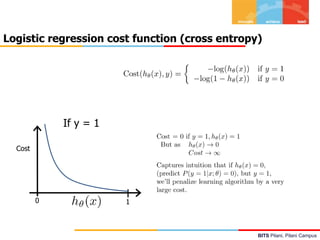
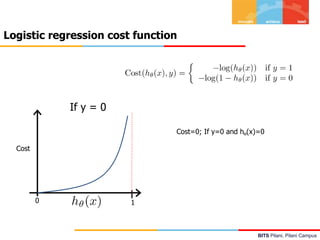
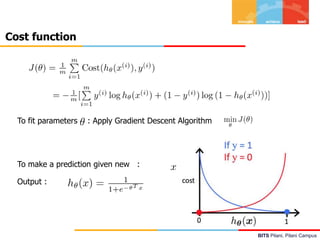




![BITS Pilani, Pilani Campus
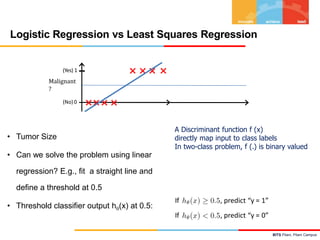
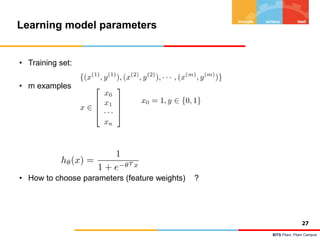
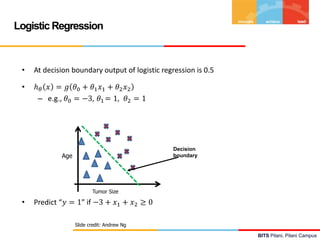
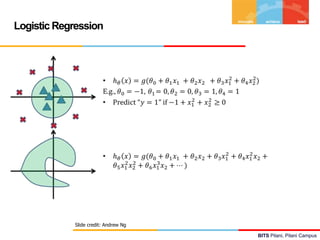
Logistic Regression – Inference & Interpretation
CGPA IQ IQ Job Offered
5.5 6.7 100 1
5 7 105 0
8 6 90 1
9 7 105 1
6 8 120 0
7.5 7.3 110 0
Assume : 0.4+0.3CGPA-0.45IQ
Predict the Job offered for a candidate : (5, 6)
h(x) = 0.31
Y-Predicted = 0 / No
Note :
The exponential function of the regression coefficient (ew-cpga) is the odds ratio associated with a one-unit
increase in the cgpa.
+ The odd of being offered with job increase by a factor of 1.35 for every unit increase in the CGPA
[np.exp(model.params)]](https://image.slidesharecdn.com/module4-linearmodelforclassification-240318104502-7393e1b2/85/Module-4-Linear-Model-for-Classification-pptx-36-320.jpg)