Embed presentation
Download to read offline


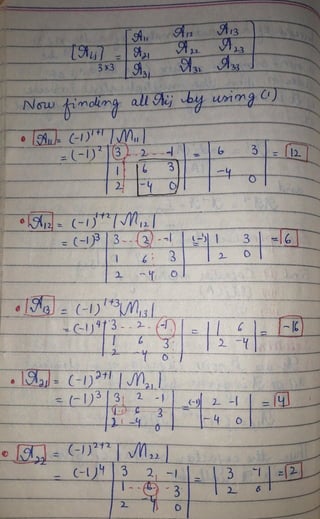
![=()3 2
3-
2
-1) 3 2
3
t-
a-GH*|JM,
-1) 3 2 -
3
A33(-1)373 2
3
2
Hence he Cojod malux o
Tt 13 6-I
42 1C
l lo I
aalj CA)= "lAJ]
-IL
1
ad (A)=
-lo 1](https://image.slidesharecdn.com/matrixinverse33-220914113242-2ad0fe6e/85/Matrix-Inverse-3x3-pdf-4-320.jpg)




1) The cofactor of an element in a matrix is obtained by deleting the row and column of that element and calculating the determinant of the resulting (m-1)x(m-1) submatrix. 2) The cofactor matrix of a matrix A is denoted by adj(A) and its elements are given by (-1)i+j times the cofactor of the element in the ith row and jth column of A. 3) For a square matrix A of order n, the adjoint of A is equal to the transpose of the cofactor matrix, or adj(A)=[AT] where AT is the transpose of A.


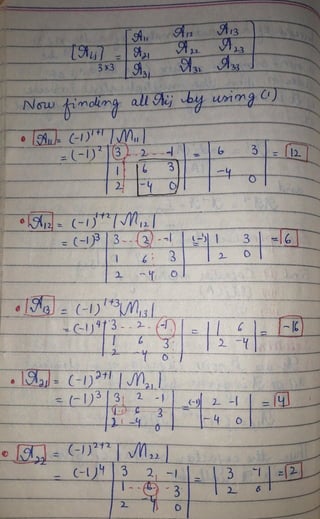
![=()3 2
3-
2
-1) 3 2
3
t-
a-GH*|JM,
-1) 3 2 -
3
A33(-1)373 2
3
2
Hence he Cojod malux o
Tt 13 6-I
42 1C
l lo I
aalj CA)= "lAJ]
-IL
1
ad (A)=
-lo 1](https://image.slidesharecdn.com/matrixinverse33-220914113242-2ad0fe6e/85/Matrix-Inverse-3x3-pdf-4-320.jpg)



