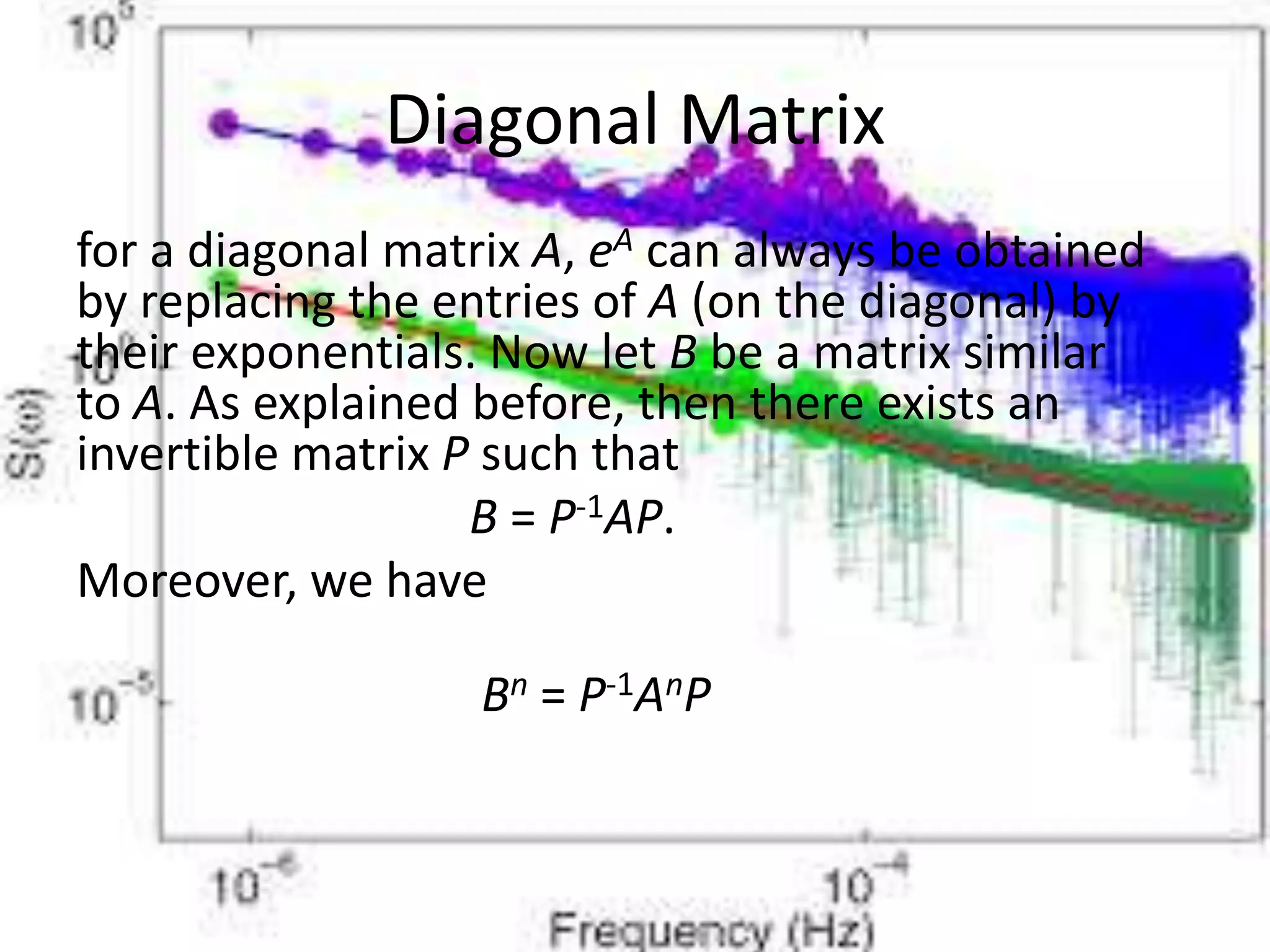
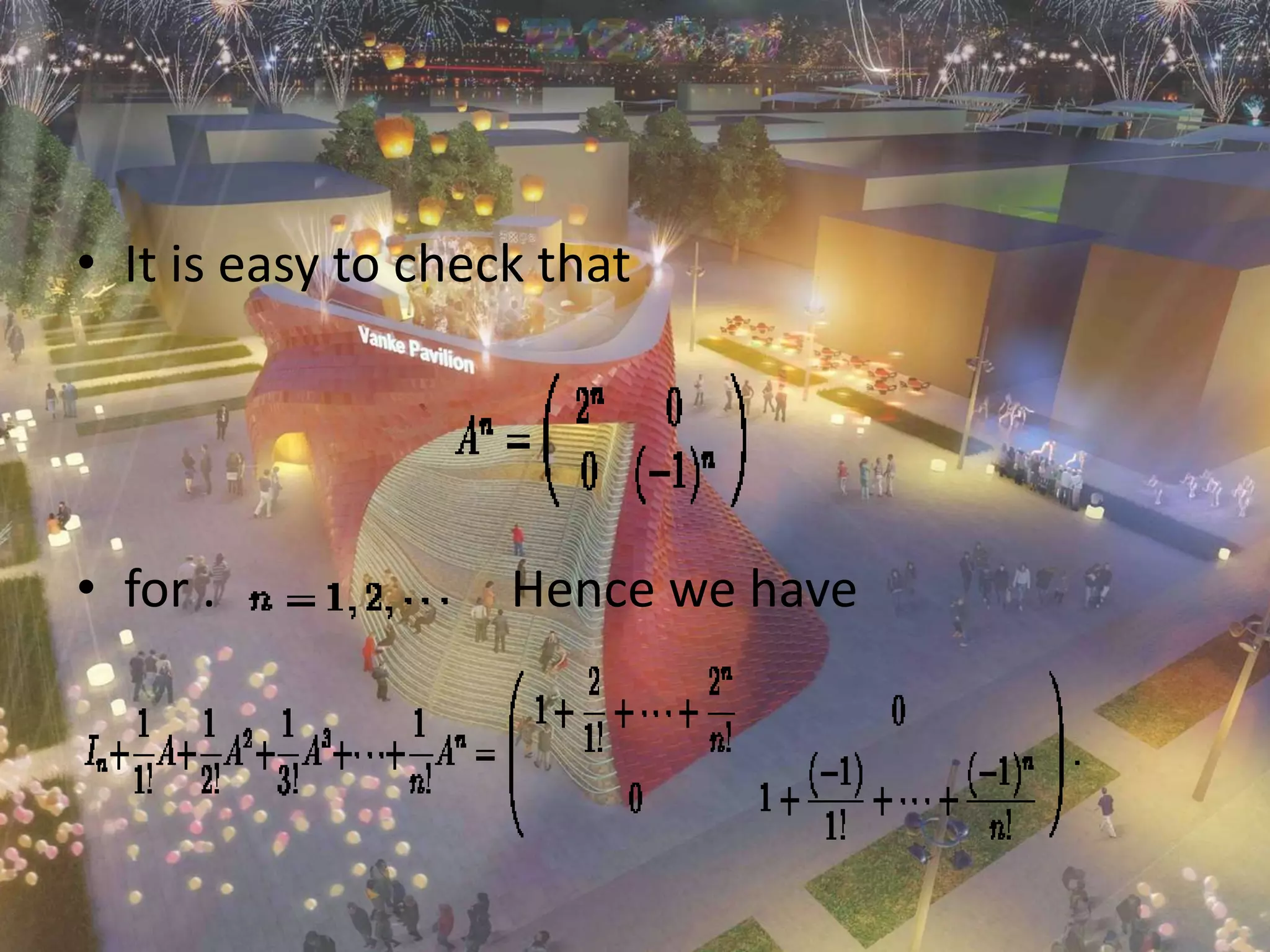This document defines the exponential of a matrix using Taylor series. It shows that the sequence of matrices (An/n!) converges to a limit matrix eA as n gets large. This defines the exponential of the matrix A. Examples are then given of calculating the exponential of diagonal and upper triangular matrices. In particular, the exponential of a diagonal matrix is obtained by taking the exponential of its diagonal entries, and the exponential of an upper triangular nilpotent matrix with zeros on the diagonal is simply the identity matrix.

1. Matrix
Exponential

2. Definition from Taylor series
The natural way of defining the exponential of a
matrix is to go back to the exponential
function ex and find a definition which is easy to
extend to matrices. Indeed, we know that the Taylor
polynomials

3. converges pointwise to ex and uniformly
whenever x is bounded. These algebraic
polynomials may help us in defining the
exponential of a matrix. Indeed, consider a
square matrix A and define the sequence of
matrices

4. When n gets large, this sequence of matrices get
closer and closer to a certain matrix. This is not
easy to show; it relies on the conclusion
on ex above. We write this limit matrix as eA.
This notation is natural due to the properties of
this matrix. Thus we have the formula

5. One may also write this in series
notation as

6. Examples

7. Consider the diagonal
matrix

8. • It is easy to check that
• for . Hence we have

9. Using the above properties of the
exponential function, we deduce that

10. Diagonal Matrix
for a diagonal matrix A, eA can always be obtained
by replacing the entries of A (on the diagonal) by
their exponentials. Now let B be a matrix similar
to A. As explained before, then there exists an
invertible matrix P such that
B = P-1AP.
Moreover, we have
Bn = P-1AnP

12. Another example of 3x3
Consider the matrix
This matrix is upper-triangular. Note that all the
entries on the diagonal are 0. These types of
matrices have a nice property. Let us discuss this
for this example. First, note that

13. In this case, we have
In general, let A be a square upper-triangular
matrix of order n. Assume that all its entries on
the diagonal are equal to 0. Then we have

14. Such matrix is called
a nilpotent matrix. In this
case, we have