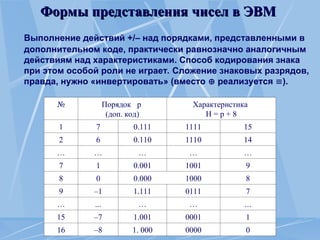
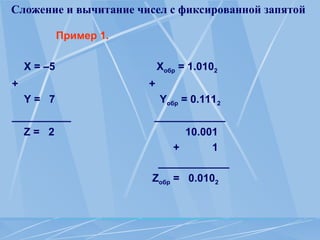
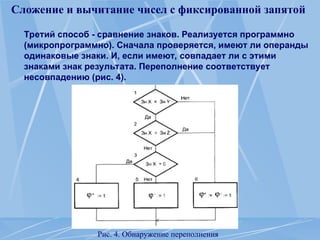
Документ представляет курс по элементам компьютерной математики, охватывающий темы машинной арифметики, представления чисел и арифметические операции с ними. Рассматриваются различные коды для представления чисел со знаком, их правила и примеры использования, а также формы представления чисел в ЭВМ. Также освещены диапазон и точность представления целых и дробных чисел, а также особенности операций сложения и вычитания.











![Коды для представления чисел со
Коды для представления чисел со
знаком
знаком
Косвенное правило: к обратному коду
отрицательного числа надо добавить единицу в
младшем разряде.
Интересной особенностью дополнительного
кода является наличие единственного кода нуля:
(0)доп = (+ 0)доп = 0.0 … 0,
Это следует из косвенного правила для (– 0):
(– 0)доп = (– 0)обр + 1 = 1.1 … 12 + 1 = [1] 0.0 … 02.
Здесь в сложении участвуют все разряды,
включая знаковый.](https://image.slidesharecdn.com/lk7-241204223303-13bc2a5f/85/Lk7-pptLk7-pptLk7-pptLk7-pptLk7-pptLk7-ppt-12-320.jpg)