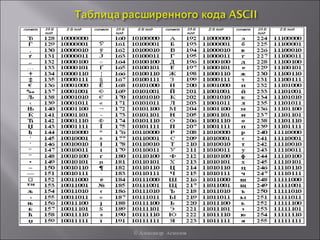
Документ описывает основы кодирования и декодирования информации, объясняя, как данные представляются в двоичном коде с использованием битов. Системы счисления, такие как десятичная, двоичная, восьмеричная и шестнадцатеричная, рассматриваются, наряду с процессами хранения чисел в компьютерах. Также упоминается использование таблиц кодировки, включая ASCII и Unicode, для представления символов в текстовой информации.