1. 03/16/10 Ìýäýýëëèéí ñèñòåì, àëãîðèòìèéí ¿íäýñ Ëåêö ¹11

2. Àãóóëãà 1. Íýã õýìæýýñò õ¿ñíýãò 2.Îëîí õýìæýýñò õ¿ñíýãò 03/16/10

3. Õ¿ñíýãò áà ò¿¿íèéã áîëîâñðóóëàõ Íýã õýìæýýñò õ¿ñíýãò Ñàíàõ îé äàõü íýã èæèë òºðëèéí ºãºãäëèéí äàðààëëûã íýã õýìæýýñò õ¿ñíýãò ãýíý. 03/16/10

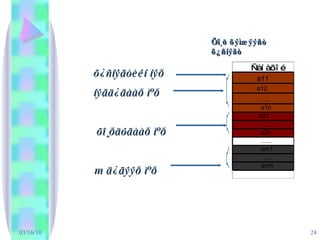
4. 03/16/10 Íýã èæèë òºðëèéí ºãºãäë¿¿äèéí äàðààëëûã ñàíàõ îéí äýñ äàðààëñàí ¿¿ðýýñ òîãòñîí ìóæèä õàäãàëæ óëìààð ýíý ìóæèéí ýõíèé õàÿã áîëîí ýëåìåíòèéí äóãààðààð íü ò¿¿íèé ýëåìåíòèéã îëæ áîëíî.

5. 03/16/10 Õ¿ñíýãò ¿¿ñãýí õýðýãëýõäýý: Íýãä¿ãýýðò: Õ¿ñíýãòèéí íýð, ýëåìåíòèéí òºðºë áîëîí ýëåìåíòèéí òîîã òîäîðõîéëæ ºãíº. ¯¿íèéã õ¿ñíýãòèéã òîäîðõîéëîõ áóþó çàðëàõ êîìàíä ãýæ íýðëýíý. Ýíý êîìàíäààð õ¿ñíýãòèéã õàäãàëàõ ñàíàõ îéã õóâààðèëäàã.

6. 03/16/10 Õ¿ñíýãòèéã òîäîðõîéëîõ ¿åä ò¿¿íèé ýëìåíòèéí òîîíû áàéæ áîëîõ õàìãèéí èõ óòãûã çààæ ºã÷ óëìààð ÿìàð÷ ¿åä õàíãàëòòàé áàéõ ñàíàõ îéã õóâààðèëæ àâäàã.

7. 03/16/10 Àëãîðèòìûí õýëýíä õ¿ñíýãòèéã áè÷èõäýý: Õ¿ñíýãòíýð(ýëåìåíòèéí_òîî); õýëáýðòýé òîäîðõîéëæ áè÷íý. Õ¿ñíýãòèéã åðäèéí õóâüñàã÷òàé íýðëýæ òýìäýãëýõ áà ýëåìåíòèéí òîîã íàòóðàë òîî ýñâýë ºìíº òîäîðõîéëñîí òîãòìîëîîð ºãíº.

8. 03/16/10 Æèøýý íü: Õ¿ñíýãò À(50), B(10); ýíä õàðãàëçàí 50, 10-í ýëåìåíòòýé õ¿ñíýãòèéã òîäîðõîéëæ áàéíà.

9. 03/16/10 Õ¿ñíýãòèéí íýð íü õ¿ñíýãòèéí ýõíèé ýëåìåíòèéí õàÿã áîëîõ ó÷ðààñ ò¿¿íèé òóñëàìæòàéãààð äóðûí I äóãààðòàé ýëåìåíòèéã îëæ àâàõ áîëîìæòîé.

10. 03/16/10 Àëãîðèòìä òîäîðõîé óòãàòàé òîãòìîëûã òîäîðõîéëæ õýðãýëäýã. Àëãîðèòìûí õýëýíä òîãòìîëûã íýð=óòãà; õýëáýðòýé èëýðõèéëëýýð òîäîðõîéëæ óëìààð ýíý íýðèéã òîãòìîë óòãûí îðîíä áè÷èæ àøãèëàíà.

11. 03/16/10 Òîãòìîë àøèãëàõ íü àëãîðèòìûí ¿éëäë¿¿äýä òîãòìîë óòãûã îëîí äàõèí áè÷èõã¿é áàéõ, ñàíàìñàðã¿é àëäàà ãàðãàõûã áàãàñãàõ, øààðäëàãàòàé ¿åä øèíýýð óòãà õÿëáàð ñîëüæ áîëîõ äàâóó òàëòàé.

12. 03/16/10 Õàðèí òîãòìîëûí íýðèéã óòãà îëãîõ ¿éëäëèéí ç¿¿í òàëä áè÷èæ øèíý óòãà îðóóëæ áîëîõã¿é, ººðººð õýëáýë àëãîðèòì äîòîð ò¿¿íèé óòãûã ººð÷èëæ áîëîõã¿é áàéäãààðàà õóâüñàã÷ààñ ÿëãààòàé.

13. 03/16/10 Òîãòìîëûã àøèãëàæ õ¿ñíýãòèéí õýìæýýã òîäîðõîéëîõ íü èë¿¿ òîõèðîìæòîé áàéäàã. Æèøýý íü: maxn=20 ; òîãòìîë õ¿ñíýãò a(maxn), c(maxn);

14. 03/16/10 Õî¸ðäóãààðò: Àëãîðèòì, ïðîãðàìä õ¿ñíýãòèéí ýëåìåíòèéã çààæ áè÷èõäýý õ¿ñíýãòèéí íýð, ýëåìåíòèéí äóãààðûã ºãíº. Äóãààðûã ºãºõ人 à1,…ai,…an; a(1),..a(i),…a(n); a[1],…a[i],…a[n] ãýõ ìýò ÿíç á¿ðèéí õýëáýðýýð áè÷äýã.

15. 03/16/10 Ãóðàâäóãààðò: Õ¿ñíýãòýíä óòãà îëãîõûí òóëä ýëåìåíòèéí óòãûã íýã íýãýýð íü îðóóëàõ ¿éëäýë þìóó ýñâýë ýëåìåíòýä íýã íýãýýð íü óòãý îëãîõ ¿éëäëèéã ãîëäóó àøèãëàíà.

16. 03/16/10 Æèøýý íü: õýðýâ maxn =20; õ¿ñíýãòà(maxn); áºãººä n<=20 áàéõ n ºãºãäñºí áîë I:=1, n ¿åä_äàâò à1:=0; äàâòàëòààð à õ¿ñíýãòèéí ýëåìåíò¿¿ä òýã óòãàòàé áîëîõ òóë õ¿ñíýãòèéã öýâýðëýõ ãýæ íýðëýäýã. I:=1, n ¿åä_äàâò îðóóë(ai);

17. äàâòàëòààð à õ¿ñíýãò òîîí óòãàòàé áîëíî. Òýãýõäýý I:=1, n ¿åä_äàâò îðóóë (ai); õýëáýðèéí äàâòàëò ìàø îëîí õýðýãëýãääýã ó÷èð ò¿¿íèéã îðóóë (ai;I=1,n) ãýæ òîâ÷èëíî. 03/16/10 Öººõºí ýëåìåíòòýé õ¿ñíýãòýíä óòãà îëãîõäîî á¿õ óòãûã òîî÷èí áè÷èõ àðãûã õýðýãëýæ áîëíî.

18. 03/16/10 ĺðºâä¿ãýýðò: Õ¿ñíýãòèéã õýâëýæ ãàðãàõäàà ìºí ýëåìåíò ýëåìåíòýýð íü ãàðãàõ ¿éëäëèéã àøèãëàíà. I:=1, n ¿åä_äàâò ãàðãà(ai); áóþó òîâ÷îîð: ãàðãà(ai; I:=1, n); õýëáýëòýé áàéíà.

19. 03/16/10 Íýã õýìæýýñò õ¿ñíýãòèéí æèøýý : Æèøýý íü1: Íàòóðàë òîî n, m áà õî¸óëàà áóóðàõààð ýðýìáëýãäñýí à1, à2,…àn áà b1, b2,…bò áîäèò òîîí äàðààëàë ºãºãäñºí áîë ýíý 2 äàðààëëûí ýëåìåíò¿¿äýýñ òîãòîõ ºñºõººð ýðýìáëýãäñýí ñ1,ñ2,…ñn+m äàðààëëûã ¿¿ñýã. Àðã m,n, à1, à2,…àn áà b1, b2,…bò ¿ð ä¿í ñ1,ñ2,…ñn+m

20. 03/16/10 àëãæ_1 mn=20; õ¿ñíýãò à(mn), b(mn), c(2*mn); îðóóë(n); îðóóë(ai; i:=1, n); îðóóë(m); îðóóë(bi; i:=1, m); I:=n, j:=m; k:=1, n+m ¿åä _äàâò {õýðýâ I>=1 áîë e:=ai ýñâýë e:=bi;

21. 03/16/10 õýðýâ j>=1 áîë d:=bi ýñâýë d:=ai; õýðýâ e<d áîë {Ck:=e; i:=i-1 } ýñâýë {Ck:=d; j:=j-1} }; ãàðãà(Ñê; K:=1, n+m) òºãñ.

22. Îëîí õýìýýñò õ¿ñíýãò Ìàòðèöèéã ñàíàõ îéä ìºð¿¿äèéí äàðààëàë áîëãîí õàäãàëõàä õî¸ð õýìæýýñò õ¿ñíýãò ãýæ íýðëýíý. 03/16/10

23. 03/16/10 Ìàòðèöèéã ñàíàõ îéä ìºð¿¿äèéí äàðààëàë áîëãîí õàäãàëõàä õî¸ð õýìæýýñò õ¿ñíýãò ãýæ íýðëýíý. Ìàòðèö íü íýã õýìæýýñò õ¿ñíýãò ìýí ó÷ðààñ íýã õýìæýýñò õ¿ñíýãò õ¿ñíýãòýýñ òîãòñîí õ¿ñíýãòèéã õî¸ð õýìæýýñò õ¿ñíýãò ãýíý

24. 03/16/10 Õî¸ð õýìæýýñò õ¿ñíýãò õ¿ñíýãòèéí íýð íýãä¿ãààð ìºð õî¸ðäóãààð ìºð m ä¿ãýýð ìºð

25. 03/16/10 Õî¸ð õýìæýýñò õ¿ñíýãòýýñ òîãòñîí õ¿ñíýãò, ãóðâàí õýìæýýñò õ¿ñíýãòýýñ òîãòñîí õ¿ñíýãò ãýõ ìýò÷èëýí n-1 õýìæýýñò õ¿ñíýãòýýñ òîãòñîí õ¿ñíýãòèéã òîäîðõîéëæ n õýìæýýñò õ¿ñíýãò ãýæ íýðýëäýã áà õî¸ð áà ò¿¿íýýñ äýýø õýìæýýñò õ¿ñíýãòèéã îëîí õýìæýýñò õ¿ñíýãò ãýæ íýðëýíý.

26. 03/16/10 N õýìæýýñò õ¿ñíýãòèéí ýëåìåíò íü n òîîíû èäåêñòýé áàéíà. ¯¿íèéã aij, aijk, aijkl ãýõ ìýò áè÷íý. Îëîí õýìæýýñò õ¿ñíýãòèéã, íýã õýìæýýñò õ¿ñíýãòòýé àäèëààð íýð áîëîí èíäåêñ á¿ðèéí àâ÷ áîëîõ õàìãèéí èõ óòãûã ºã÷ òîäîðõîéëíî.

27. 03/16/10 Æèøýý íü: Õ¿ñíýãò íýð (ìºðèéí_òîî, áàãàíûí_òîî ) maxn=20 õ¿ñíýãò a(50, 20), b(5,10); õ¿ñíýãò c(maxn, 5), b(10,maxn);

28. 03/16/10 Îëîí õýìæýýñò õ¿ñíýãòýíä óòãûã îðóóëàõ áà ãàðãàõäàà äàâòàëò àøèãëàäàã. Æèøýý íü: max=10; õ¿ñíýãò a(max, max); ̺ð áàãàíûí òîî ºãºãäñºí áîë I:=1, n ¿åä_äàâò

29. 03/16/10 j:=1, m ¿åä_äàâò îðóóë (aij) Ýíý äàâòàëòûã òîâ÷èëæ Îðóóë (aij; I:=1, n; j:=1, m); ¯¿íòýé àäèëààð ãàðãàõ ¿éëäëèéã ãàðãà(aij; I:=1,n; j:=1, m); áè÷íý.

30. 03/16/10 Îëîí õýìæýýñò õ¿ñíýãòèéí æèøýý : Æèøýý íü 2: ªãºãäñºí a(n,n) êâàäðàò ìàòðèöèéí õºíäëºí äèàãîíàëààñ õîéøèõ ýëåìåíò¿¿äèéí min îë. Àðã n- íàòóðàë òîî ¿ð ä¿í (a min)

31. 03/16/10 Àëãæ2 mn=5; õ¿ñíýãò a(mn, mn); îðóóë (n); îðóóë (aij; I:=1,n; j:=1, n ); amin:=a1n; I:=2, n ¿åä_äàâò õýðýâ aij<amin áîë amin:=aij ãàðãà(amin) òºãñ.