Recommended
PPT
перетворення графіків тригонометричних виразів
PPT
PPT
PPTX
FISMArts - Improving Retention of FISMA Guidance Details with Mnemosyne
PPT
PPT
My Sister Puts The Peanut Butter In The Freezer
PPT
Domino must gather information
PDF
Chuong 6 nhung nen tang cua tang truong
PPTX
Updated Year to Date Comparison
ODP
PPTX
Appearances do matter leadership in a crisis
PDF
Chuong 4 thach thuc tham hut thuong mai
PPS
Photofraphy by Solve Sundsbo
PPT
Annette Kurman, Assisted Living presentation
PPTX
TiếP Thị Số HướNg DẫNthiếT YếU Cho
PDF
PPTX
When 6 stages of the consumer buying process meet internet word of mouth
PDF
PDF
Chuong 3 bat on thi truong tai chinh
PDF
Installation Instructions Tachometerwith Counter Drehzahlmessermit Zaehler
PDF
Ensembl Plants: Visualising, mining and analysing crop genomics data
PDF
Onemma - Looking to the Future
PDF
Collaborative Creative Writing
PPT
Janssen immune system_&_microbiome_022213 (1)
PDF
Chuong 2 rui ro tham hut tai khoa
PDF
Press Release Vietnam 2009 English
DOCX
положення 2025-2026.docxположення 2025-2026.docxположення 2025-2026.docxполож...
DOCX
1.8 нове.docx1.8 нове.docx1.8 нове.docx1.8 нове.docx1.8 нове.docx1.8 нове.doc...
PPTX
Довідник бакалавра Кафедри обліку, аудиту та оподаткування
DOCX
про учн.самоврядування ЗМІНИ.docxпро учн.самоврядування ЗМІНИ.docx
More Related Content
PPT
перетворення графіків тригонометричних виразів
PPT
PPT
PPTX
FISMArts - Improving Retention of FISMA Guidance Details with Mnemosyne
PPT
PPT
My Sister Puts The Peanut Butter In The Freezer
PPT
Domino must gather information
PDF
Chuong 6 nhung nen tang cua tang truong
Viewers also liked
PPTX
Updated Year to Date Comparison
ODP
PPTX
Appearances do matter leadership in a crisis
PDF
Chuong 4 thach thuc tham hut thuong mai
PPS
Photofraphy by Solve Sundsbo
PPT
Annette Kurman, Assisted Living presentation
PPTX
TiếP Thị Số HướNg DẫNthiếT YếU Cho
PDF
PPTX
When 6 stages of the consumer buying process meet internet word of mouth
PDF
PDF
Chuong 3 bat on thi truong tai chinh
PDF
Installation Instructions Tachometerwith Counter Drehzahlmessermit Zaehler
PDF
Ensembl Plants: Visualising, mining and analysing crop genomics data
PDF
Onemma - Looking to the Future
PDF
Collaborative Creative Writing
PPT
Janssen immune system_&_microbiome_022213 (1)
PDF
Chuong 2 rui ro tham hut tai khoa
PDF
Press Release Vietnam 2009 English
Recently uploaded
DOCX
положення 2025-2026.docxположення 2025-2026.docxположення 2025-2026.docxполож...
DOCX
1.8 нове.docx1.8 нове.docx1.8 нове.docx1.8 нове.docx1.8 нове.docx1.8 нове.doc...
PPTX
Довідник бакалавра Кафедри обліку, аудиту та оподаткування
DOCX
про учн.самоврядування ЗМІНИ.docxпро учн.самоврядування ЗМІНИ.docx
DOCX
монітоаааринг 1.17 новеWord Document.docx
PPTX
Академічна доброчесність. Kафедрa обліку, аудиту та оподаткування
DOCX
Статут_Учнівського_Самоврядування_Запал_обєднаний.docx
PPTX
Презентація спеціальності “Облік і оподаткування”
PPTX
Проголошення Акту Злуки та утворення Соборної Української держави
PPTX
Неформальна освіта. Кафедра обліку, аудиту та оподаткування
Lecture3 1. 2. 3. 4. 7. 15. Развитието на една функция в Тейлоров ред в общ вид е
F(X) = f{(x1+h1), {(x2+h2), . . ., {(xn+hn)} = f (x1, x2, . . . , xn) +
+ ∂f/∂x1.h1 + ∂f/∂x2.h2 + …+ ∂f/∂xn.hn + …
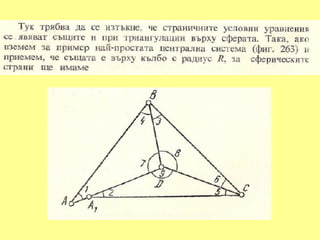
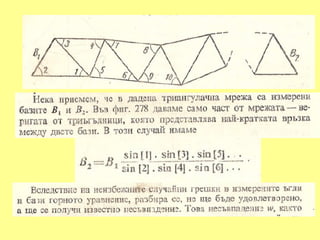
16. sin {(1) + v1}. sin {(3) + v3}. sin {(5) + v5}
F(X) = ─────────────────────────── - 1 = 0
sin {(2) + v2}. sin {(4) + v4}. sin {(6) + v6}
cos (1). sin (1). sin (3). sin (5) cos (2). sin (1). sin (3). sin (5)
F(X) = F (0) + ───────────────── v1- ────────────────── v2 +
sin (1). sin (2) . sin (4). sin (6) sin2 (2). sin (4). sin (6)
cos (3). sin (3). sin (1). sin (5) cos (4). sin (1). sin (3). sin (5)
+ ───────────────── v3 - ────────────────── v4 + . . . = 0
sin (3). sin (2) . sin (4). sin (6) sin2 (4). sin (4). sin (6)
Където
sin (1). sin (3). sin (5)
F (0) = ─────────────
sin (2) . sin (4). sin (6)
17. Означаваме : ctg (i) / ρcc = αi , където ρcc = 636620
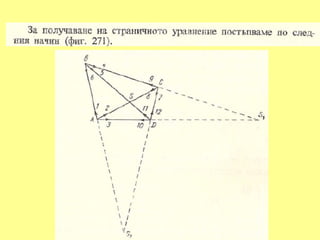
Тогава за страничното уравнение в окончателен линеен вид се
получава
α1 v1 - α2v2 + α3v3 - α4v4 + α5v5 - α6v6 + w = 0
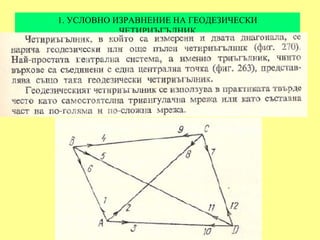
Така условните уравнения за по-голямата централна система ще
бъдат
21. Общ вид на нормалните уравнения на корелатите :
[aa]K1 + [ab]K2 + [ac]K3 + . . . . . . . . . + [ar]Kr + w1 = 0
[ab]K1 + [bb]K2 + [bc]K3 + . . . . . . . . . + [br]Kr + w2 = 0
[ac]K1 + [bc]K2 + [cc]K3 + . . . . . . . . . + [cr]Kr + w3 = 0
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
[ar]K1 + [br]K2 + [cr]K3 + . . . . . . . . . . + [rr]Kr +wr = 0
vi = ai K1 + bi K2 + ci K3+ . . . . . + ri Kr
me = ± √[vv] / r
22. [aa/p]K1 + [ab/p]K2 + [ac/p]K3 + . . . . . . . . . + [ar/p]Kr + w1 = 0
[ab/p]K1 + [bb/p]K2 + [bb/p]K3 + . . . . . . . . . + [br/p]Kr + w2 = 0
[ac/p]K1 + [bc/p]K2 + [cc/p]K3 + . . . . . . . . . + [cr/p]Kr + w3 = 0
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
[ar/p]K1 + [br/p]K2 + [cr/p]K3 + . . . . . . . . . . + [rr/p]Kr + wr = 0
vi = ai/pi K1 + bi/pi K2 + ci/pi K3+ . . . . . + ri/pi Kr
me = ± √[pvv] / r
25. 33. 43.
















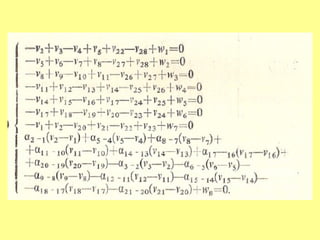
![Общ вид на нормалните уравнения на корелатите :
[aa]K1 + [ab]K2 + [ac]K3 + . . . . . . . . . + [ar]Kr + w1 = 0
[ab]K1 + [bb]K2 + [bc]K3 + . . . . . . . . . + [br]Kr + w2 = 0
[ac]K1 + [bc]K2 + [cc]K3 + . . . . . . . . . + [cr]Kr + w3 = 0
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
[ar]K1 + [br]K2 + [cr]K3 + . . . . . . . . . . + [rr]Kr +wr = 0
vi = ai K1 + bi K2 + ci K3+ . . . . . + ri Kr
me = ± √[vv] / r](https://image.slidesharecdn.com/lecture3-090714145446-phpapp02/85/Lecture3-21-320.jpg)
![[aa/p]K1 + [ab/p]K2 + [ac/p]K3 + . . . . . . . . . + [ar/p]Kr + w1 = 0
[ab/p]K1 + [bb/p]K2 + [bb/p]K3 + . . . . . . . . . + [br/p]Kr + w2 = 0
[ac/p]K1 + [bc/p]K2 + [cc/p]K3 + . . . . . . . . . + [cr/p]Kr + w3 = 0
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
[ar/p]K1 + [br/p]K2 + [cr/p]K3 + . . . . . . . . . . + [rr/p]Kr + wr = 0
vi = ai/pi K1 + bi/pi K2 + ci/pi K3+ . . . . . + ri/pi Kr
me = ± √[pvv] / r](https://image.slidesharecdn.com/lecture3-090714145446-phpapp02/85/Lecture3-22-320.jpg)