References Weisstein, Eric W. "Poisson Distribution." MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/PoissonDistribution.html Stat Trek. "Poisson Distribution: Definition & Examples." https://stattrek.com/probability-distributions/poisson.aspx Khan Academy. 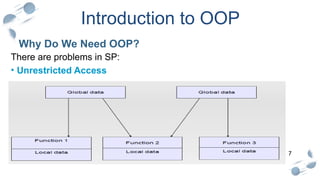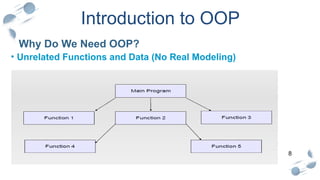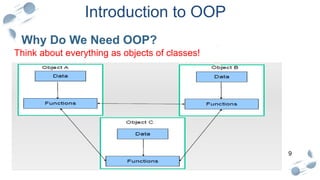"Poisson Distribution." https://www.khanacademy.org/math/statistics-probability/random-variables-stats-librarynderstanding the Poisson Distribution The Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space, provided these events occur with a known constant mean rate and independently of the time since the last event. It is named after the French mathematician Siméon Denis Poisson. When to Use the Poisson Distribution The Poisson distribution is used when: Events are independent. The average rate (events per time or space unit) is constant. Two events cannot occur at exactly the same instant. The probability of more than one event happening in an infinitesimally small time interval is negligible. Examples include: The number of emails received in an hour. The number of accidents at an intersection per month. The number of decay events per second from a radioactive source. The Formula The Poisson probability mass function is: 𝑃 ( 𝑋 = 𝑘 ) = 𝜆 𝑘 𝑒 − 𝜆 𝑘 ! P(X=k)= k! λ k e −λ ​ Where: 𝑃 ( 𝑋 = 𝑘 ) P(X=k) is the probability of k events in a fixed interval. 𝜆 λ (lambda) is the average number of events per interval. 𝑒 e is Euler’s number (approximately 2.71828). 𝑘 k is the number of events (k = 0, 1, 2, ...). 𝑘 ! k! is the factorial of 𝑘 k. 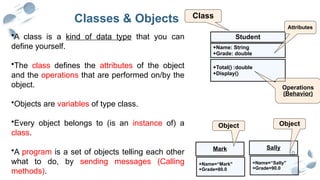Mean and Variance One interesting property of the Poisson distribution is that its mean and variance are both equal to λ. This is useful for identifying if a data set may follow a Poisson distribution. Graphical Representation The shape of a Poisson distribution depends on the value of λ: If λ is small (e.g., 1 or 2), the distribution is skewed to the right. As λ increases, the distribution becomes more symmetric and approaches a normal distribution. Real-World Applications The Poisson distribution has many practical uses in fields such as: Operations research: modeling customer arrivals at a service point. Biology: modeling mutation counts in genes. Telecommunications: modeling packet arrivals in a network. Insurance: modeling claim frequencies. Limitations While the Poisson distribution is powerful, it has limitations. It assumes events occur independently and at a constant rate, which may not always be true in real-world situations. Overdispersion (variance > mean) may indicate that a Negative Binomial Distribution is a better fit.

1. Object Oriented Programming
Lab 1

2. 2
Agenda • Logistics
• Introduction to OOP
• Main OOP Vocabulary
• Getting started with IntelliJ
• How to install
• Quick start Guide
• Displaying outputs
• How to run / debug ?
• Hands-on

3. 3
Logistics
• Attendance is recorded weekly at the start of the lab.
• You have a 10-minute grace period for arrival.
• If you arrive more than 10 minutes late, you can stay, but you will be
marked absent.
• Critical: Exceeding 3 absences will prohibit you from taking the final exam.

4. 4
Logistics - Grading Policy
• Final Grade Breakdown:
• 60% Semester Work
• 40% Final Exam
• There are NO points for attendance.
• Semester Work (60 points) includes:
• Midterm Exam: 20 points
• Quizzes: A minimum of 2 is mandatory.
• Other Activities: Assignments, lab work, and projects.

5. OOP ?

6. 6
Introduction to OOP
• OOP is captured from real life, we always deal with different
types of objects. cars, mobiles, PCs, etc…
• All of these are objects that have particular behavior and
attributes.
• OOP can be defined as a programming paradigm where a
software system is represented as a collection of objects
that interact with each other to solve the overall task.

7. 7
Introduction to OOP
Why Do We Need OOP?
There are problems in SP:
• Unrestricted Access

8. 8
Introduction to OOP
Why Do We Need OOP?
• Unrelated Functions and Data (No Real Modeling)

9. 9
Why Do We Need OOP?
Think about everything as objects of classes!
Introduction to OOP

10. 10
Classes & Objects
•A class is a kind of data type that you can
define yourself.
•The class defines the attributes of the object
and the operations that are performed on/by the
object.
•Objects are variables of type class.
•Every object belongs to (is an instance of) a
class.
•A program is a set of objects telling each other
what to do, by sending messages (Calling
methods).
Mark
+Name=“Mark"
+Grade=80.0
Sally
+Name=“Sally"
+Grade=90.0
Object Object
Student
+Name: String
+Grade: double
+Total() :double
+Display()
Class
Attributes
Operations
(Behavior)

11. 11
OOP Concepts

12. 12
OOP Concepts
•Encapsulation: Bundling data and the methods that work on that data within one unit, like a class.
•Abstraction: Hiding the complex reality while exposing only the essential parts.
•Inheritance: A mechanism where a new class inherits attributes and methods from an existing class.
•Polymorphism: The ability of a method or object to take on many different forms.

13. 13
Before JAVA

14. 14
Software Development Tools
Editor
Source
code
Compiler
Object
code
Linker
Executable
program
Editor Source
code
Compiler
Object
code
Editor Source
code
Interpreter

15. 15
Introduction to Java
• Java is platform-independent: the same program can run on any
correctly implemented Java system using an appropriate JRE or JVM.
• Java is object-oriented: Structured in terms of classes, which group
data with operations on that data.
• This course mainly focuses on J2SE.

16. 16
Installation
.
• JVM is the virtual engine and one which
enables byte code support.
• JRE contains JVM and all the other
libraries to run Java applications. It is
enough to run any Java application.
• JDK is a superset that comprises JVM, JRE,
and the tools to develop Java
applications. Its primary objective is to
provide support for the build and
compilation.

17. 17
JIT Code
Generator

18. 18
18
Different IDEs
• An Integrated Development Environment is a computer software
to help computer programmers develop software.
• The Leaders:
- NetBeans
- Microsoft Visual Studio
- Eclipse
- Visual Code
- IntelliJ

19. 19
Packages in JAVA
• A group of related classes.
• To guarantee a unique package name, use your company‘s Internet
domain name (which is known to be unique) written in reverse.
• For example, oracle.com is a domain when written in reverse order,
it turns into the package name com.oracle
• Packages can be nested.
• Standard Java Packages: java.* , javax.*
• such as java.lang, java.util, java.net, and so on

20. 20
Packages
If the same class “Date” exists in
two packages and they are
imported in the project , I have to
specify which date I want to use:
import java.util.*;
import java.sql.*;
import java.util.Date;
Date today;
Or
java.util.Date deadline;
java.sql.Date today;
A class can use all classes from its own
package and all public classes from other
packages.
To access public classes in other packages we
use the key word import
import java.util.Date;
Or we can import all classes in a package
import java.util.*;

21. 21
Displaying outputs
• To Output the message we use:
• Print: shows value passed to it.
System.out.print (" …");
System.out.print (" Hello");
• Println: shows value followed by new Line
System.out.println(" …");
System.out.println (" Hello");
• Printf: shows value with a certain format
System.out.printf(….);

22. 22
Displaying Outputs: Printf(…)
• System.out.printf(“%parameter”, value);
• Common parameters:
'd': decimal integer
'f': decimal notation for float
'c': for a character
's': for a string.
'b': for a boolean value  "true" or "false"
'o': octal integer
'x': hexadecimal integer
'n': "%n" has the same effect as "n".

23. 23
Displaying outputs: Printf(...) cont’
• Examples:
1. System.out.printf(“%s”, “Hello”);  Hello
2. String str=“hello”;
System.out.printf(“%s”, str); hello
3. System.out.printf(“%d”, 10);  10
4. int x=10;
System.out.printf(“%s=%d”, “x”, x);  x=10
5. int x=1000;
System.out.printf(“%,d”, x);  1,000
6. float y =5.365f;
System.out.printf(“%.1f”, y);  5.4
If you didn’t write f
after the number there
will be an error as any
decimal number is of
a double type “by
default”
.1 means round to the
nearest 1 decimal
number.
So .5 means round to
the nearest 5
decimals

24. 24
Displaying Outputs Cont’

25. 25
Exercise 1: HelloWorld
int z=1500000;
double y=1000.525435;
String mrX="X";
char currency='$';
X said:"I have 1,500,000$”
Y said:"Ok MrX, I have 1000.525$"

26. 26
Reading Input from User
• To read something from the console:
1. Import the package that has the class Scanner.
(The import line is to be written under the name of
your package)
 import java.util.Scanner;
2. Take an object from the Scanner class.
 Scanner input =new Scanner(System.in) ;
3. Use the Scanner suitable method to read the
next input according to its data type.
e.g. int x=input.nextInt();
float f= input.nextFloat();
String s= input.next();
char c = input.next().charAt(0);

27. 27
Exercise 2: Adding Two
Numbers Read from user
Scanner Object
Read First Number
using Scanner
Object
Show Sum
Show message to
enter first number
Same steps with
second number
Import package containing scanner class

28. 28
Hands on #1: Quadratic Equation
• Consider the following quadratic equation:
3X2
-8X + 4
• Write a program that reads X from user and shows result.
• Try the following values
• X=2 the result will be zero.
• X=200 the result will be 118404.
• X=1 the result will be -1.
10 Minutes

29. 29
solution

30. 30
Hands on #2: Temperature Converter
• Write a program to convert temperature from Fahrenheit to
Celsius and vice versa.
• From Fahrenheit to Celsius :
Celsius = ( ( Fahrenheit - 32 ) * 5 / 9 )
• From Celsius to Fahrenheit :
Fahrenheit = ( ( Celsius * 9 ) / 5 ) + 32

31. 31
Hands on #2: Temperature Converter
• Implement two methods (functions) for conversion.
• Read Temperature and type to convert to from user.
• Display converted temperature .
• Test:
• Enter (26) and convert it
to Fahrenheit which will be
(78.8)
20 Minutes

32. 32
Solution

33. 33
Solution cont’

34. THANK YOU