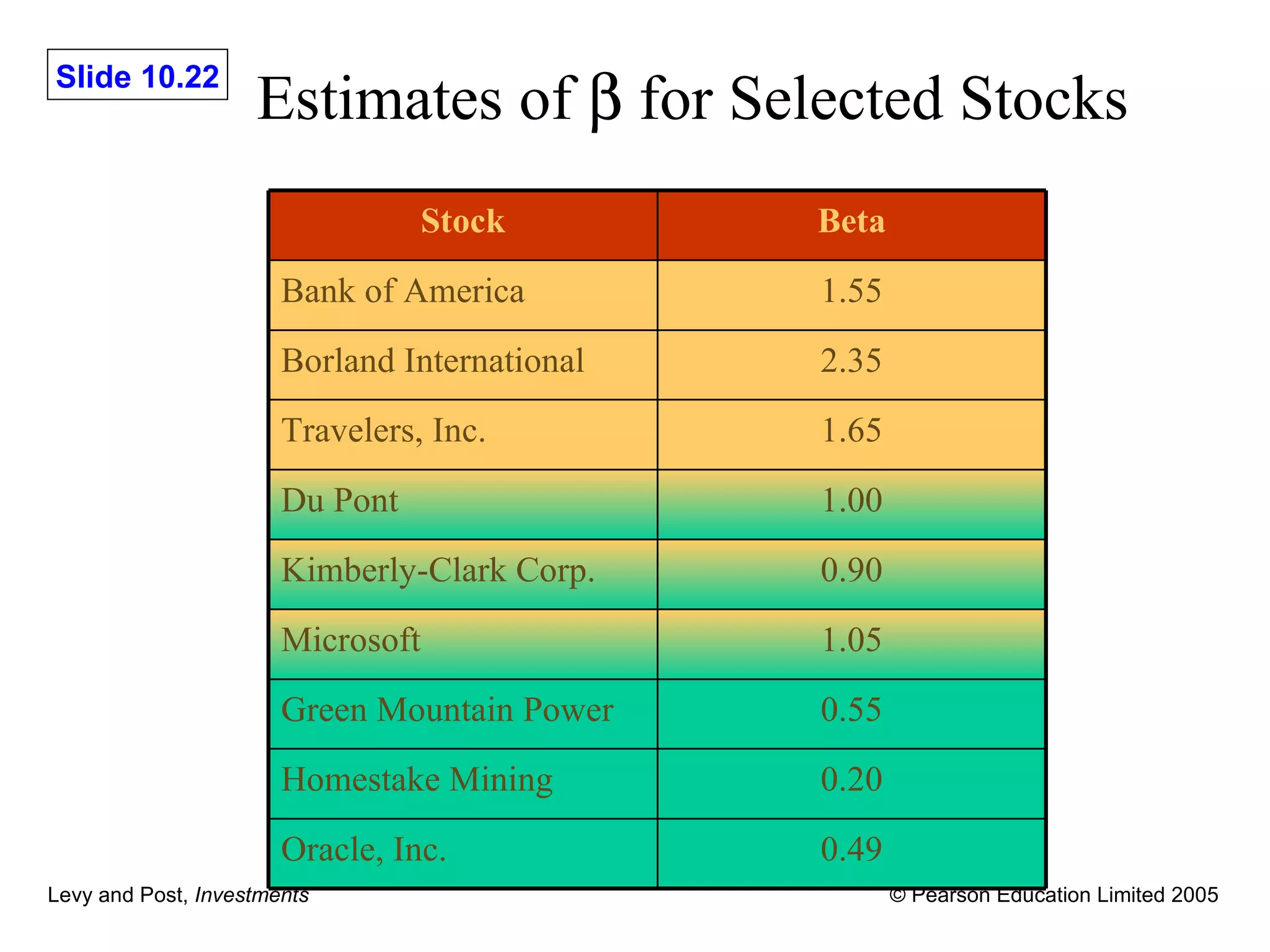
The document provides an overview of the Capital Asset Pricing Model (CAPM). It defines key concepts such as systematic and non-systematic risk, the security market line, and beta. It also discusses how beta is estimated using regression analysis and the characteristic line. Empirical tests are often used to evaluate whether asset prices conform to the predictions of the CAPM.

1. Investments Chapter 10: The Capital Asset Pricing Model

2. Two Definitions Explained Asset Pricing Theories Asset pricing theories try to explain the expected rates of return of assets and why they differ both among each other and over time. Equilibrium Rates of Return A market is in equilibrium when all investors hold their optimal portfolio and hence there is no reason for further transactions.

3. The Basic Question of the CAPM ‘ What are the equilibrium rates of return if all investors apply the mean-variance criterion to an identical mean-variance efficient set?’

4. Two Additional Concepts Introduced in the CAPM Framework The Risk-free Asset The rate of return this asset is known with certainty. (Short-term treasury bills often proxy for the risk-free rate) The Market Portfolio Includes all available risky capital at their relative market value.

5. Assumptions Behind the CAPM The capital market is characterized by perfect competition. All investors choose their portfolio according to the mean-variance criterion. All investors have homogeneous expectations regarding the future in terms of means, variances and covariances. (This implies investors have the same investment horizon.) Investors can borrow and lend at the risk-free rate. UNDER THESE ASSUMPTIONS ALL INVESTORS FACE IDENTICAL EFFICIENT FRONTIERS.

6. The Opportunity Line: I Assumptions: 1. Investor can borrow and lend at the risk-free rate. 2. Investor can invest in one risky asset. Under these assumption the expected return of this portfolio is a linear positive relation of the standard deviation of the risky asset.

7. The Opportunity Line: II - Illustration Exhibit 10.1 Investment opportunities with risk-free asset Source: From Introduction to Investments , 2nd edn, by Levy. © 1999. Reprinted with permission of South-Western, a division of Thomson Learning: www.thomsonrights.com. Fax 800 730-2215.

8. The Capital Market Line: I Opportunity line assumes one available risky asset. The capital market line (CML) drops this assumption. Investors can invest in many risky assets, creating many opportunity lines. It can be shown that investors will choose the same portfolio of risky assets , maximizing the slopes of the individual opportunity lines, known as the tangency portfolio.

9. The Capital Market Line: II Since all investors hold the tangency portfolio, this portfolio equals the market portfolio. By mixing the market portfolio with borrowing and lending of the risk-free asset one gets a linear positive line analogous to the opportunity line. But, note that the market portfolio is not an individual asset. By mixing it with the risk-free rate, we end up holding a portfolio of risky assets and the risk-free asset.

10. The Separation Principle Given the assumptions behind the CAPM, and the resulting CML, one can separate the investment process into two stages: 1. Determining the market portfolio Because all investors hold the same portfolio, there ’s no need to know investors’ individual preferences at this stage. 2. Adjusting the return characteristics by mixing the market portfolio with the risk-free asset This stage is based on each investor ’s individual preferences.

11. Separating Systemic from Nonsystemic Risk Under the separation principle all investors hold the market portfolio. The relevant risk measure for an individual asset than logically becomes its contribution to the risk of the market portfolio. Consequently, investors need to be compensated for bearing systemic risk but not for non-systemic risk.

12. Definition of Risk When Investors Hold the Market Portfolio Researchers have shown that the best measure of the risk of a security in a large portfolio is the beta (  )of the security. Beta measures the responsiveness of a security to movements in the market portfolio.

13. Aggressive, Neutral and Defensive Assets Aggressive Asset  i > 1, asset i has more (systematic) risk than the market. Neutral Asset  i  1, asset i has the same (systematic) risk as the market. Defensive Asset  i < 1, asset i has less (systematic) risk than the market.

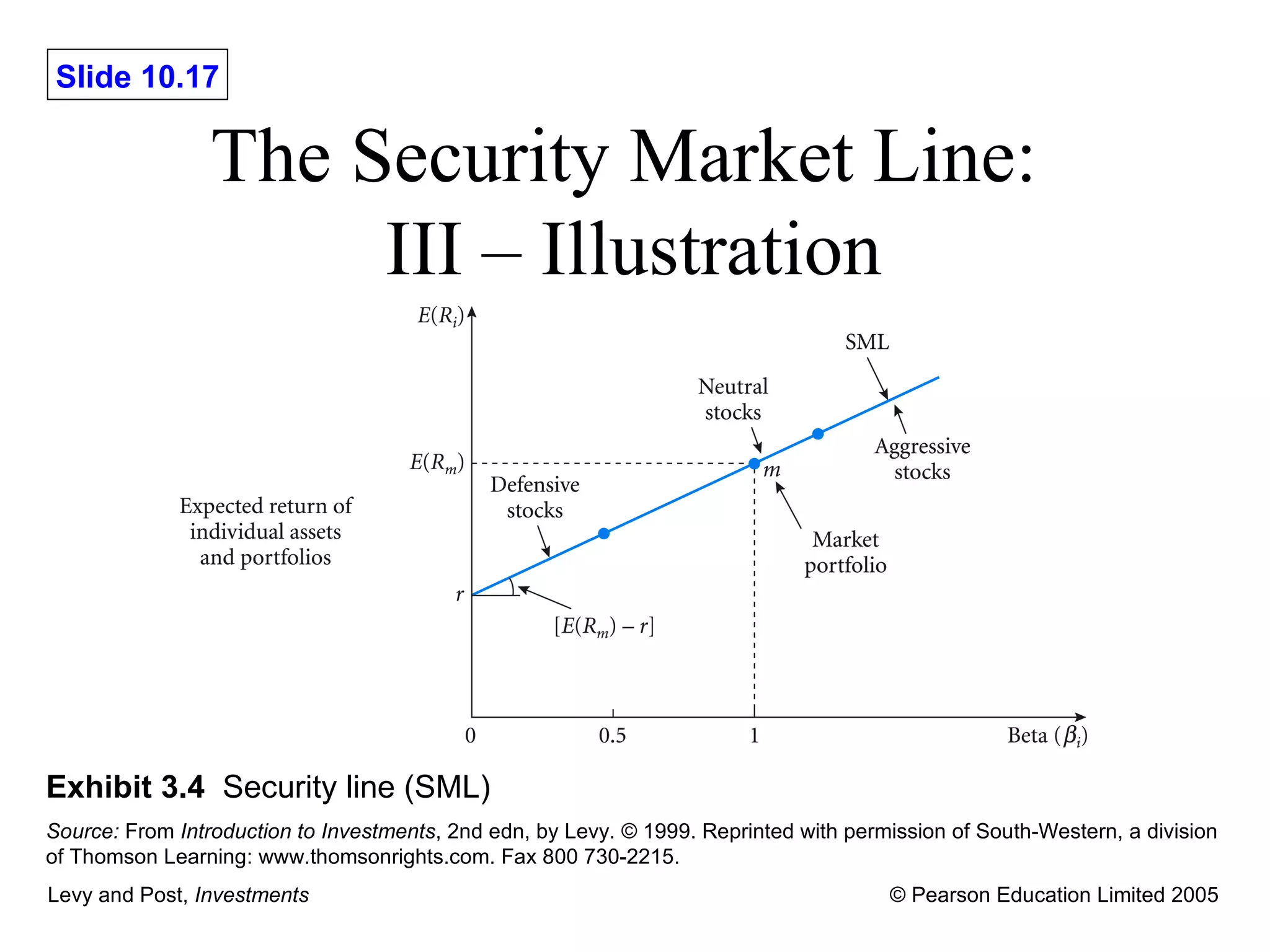
14. The Security Market Line: I Under the assumptions of the CAPM, only compensating investors for bearing systemic risk, the following linear risk-return relation (for both individual assets and portfolios) should hold: E ( R i )  r  [ E ( R m ) – r ]   i    Expected Rate of Return  Risk-Free Rate  Risk Premium

15. Expected Return on an Individual Security This formula is called the Capital Asset Pricing Model (CAPM) Assume  i = 0, then the expected return is R F . Assume  i = 1, then Expected return on a security = Risk-free rate + Beta of the security × Market risk premium

16. The Security Market Line: II – The Risk Premium The risk premium is the expected return investors require above and beyond what can be earned on the risk-free asset: [ E ( R m ) – r ]   i  market risk premium Asset i’s Beta

17. The Security Market Line: III – Illustration Exhibit 3.4 Security line (SML) Source: From Introduction to Investments , 2nd edn, by Levy. © 1999. Reprinted with permission of South-Western, a division of Thomson Learning: www.thomsonrights.com. Fax 800 730-2215.

18. Estimating an Asset ’s Beta: I – The Characteristic Line Besides being an indication of the relative riskiness of an asset, the beta also measures the sensitivity to market movements . The regression line describing the relationship between Ri (Return on Asset i ) and Rm (Return on Market Portfolio) is called the characteristic line of Asset i .

19. Estimating an Asset ’s Beta: II – The Characteristic Line Exhibit 10.4 Examples of the characteristic line Source: From Introduction to Investments , 2nd edn, by Levy. © 1999. Reprinted with permission of South-Western, a division of Thomson Learning: www.thomsonrights.com. Fax 800 730-2215.

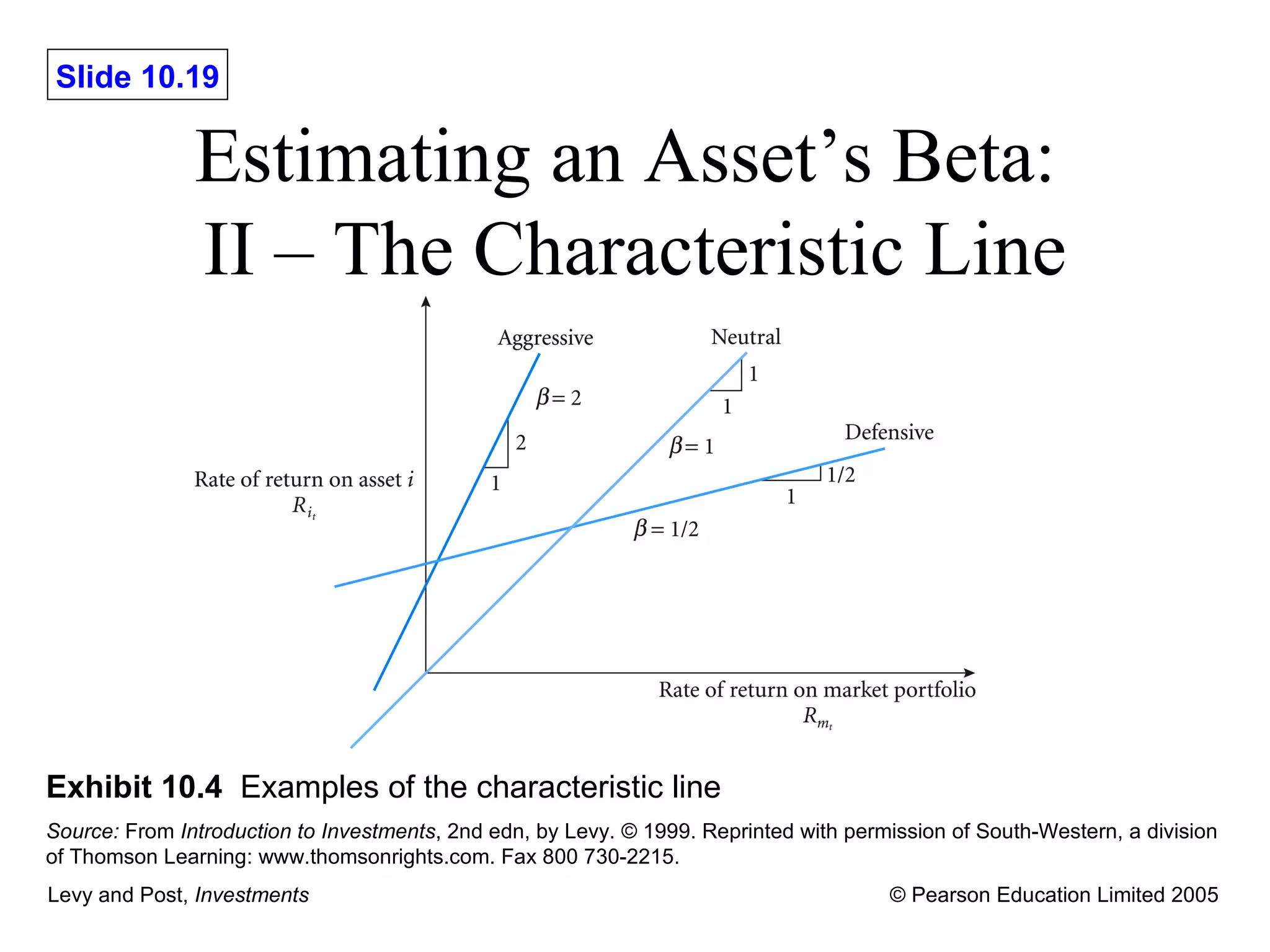
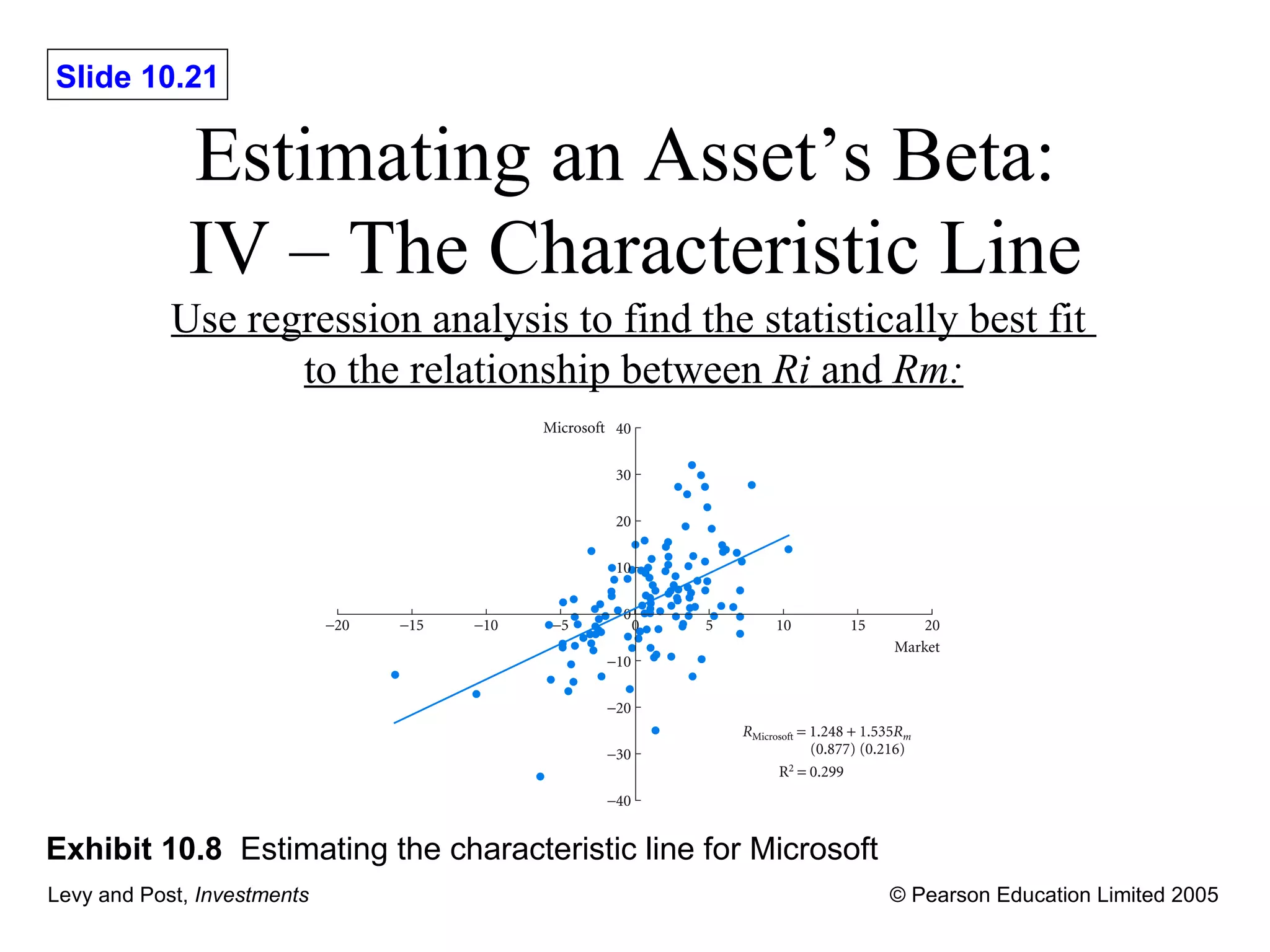
20. Estimating an Asset ’s Beta: III – The Characteristic Line The Characteristic Line can be written as: R i – r   i   i  R m – r ]  e i  i intercept of the regression line  i slope of the regression line e t firm-specific factor with mean E ( e i )=0 and variance  2 e,i

21. Estimating an Asset ’s Beta: IV – The Characteristic Line Use regression analysis to find the statistically best fit to the relationship between Ri and Rm: Exhibit 10.8 Estimating the characteristic line for Microsoft

22. Estimates of  for Selected Stocks Stock Beta Bank of America 1.55 Borland International 2.35 Travelers, Inc. 1.65 Du Pont 1.00 Kimberly-Clark Corp. 0.90 Microsoft 1.05 Green Mountain Power 0.55 Homestake Mining 0.20 Oracle, Inc. 0.49

23. Theoretical Extensions of the CAPM Zero-beta model. GCAPM. ICAPM. CCAPM. 3M CAPM.

24. Empirical Validity of the CAPM Two tests: Check if the underlying assumptions of the CAPM are realistic. Empirically test the degree to which the CAPM predicts actual security prices.

25. Empirically Testing the Predictions of the CAPM Often-used method: Two-Pass Regression Methodology Step 1 : Establish sample data. Step 2 : Estimate characteristic lines. Step 3 : Estimate the security market line. Step 4 : Test predictions of the CAPM.

26. CAPM Anomalies Several phenomena discovered that seem inconsistent with the CAPM: 1. The size effect. 2. The value effect. 3. The momentum effect.

27. Methodological Problems in Testing the CAPM Benchmark error. Time variation of the return distribution. Statistical problems with the test methodology. Data mining, data snooping and sample selection bias.