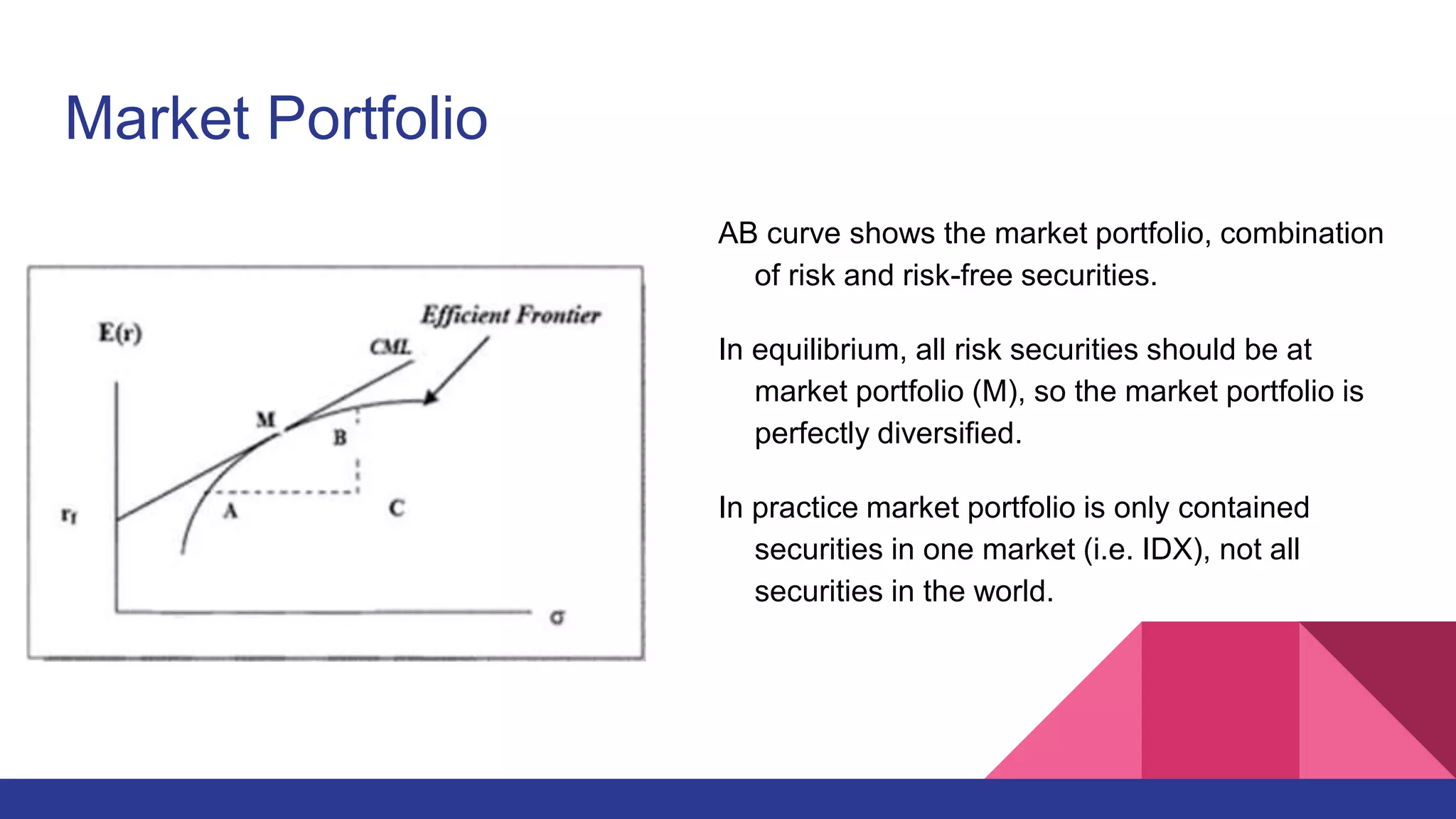
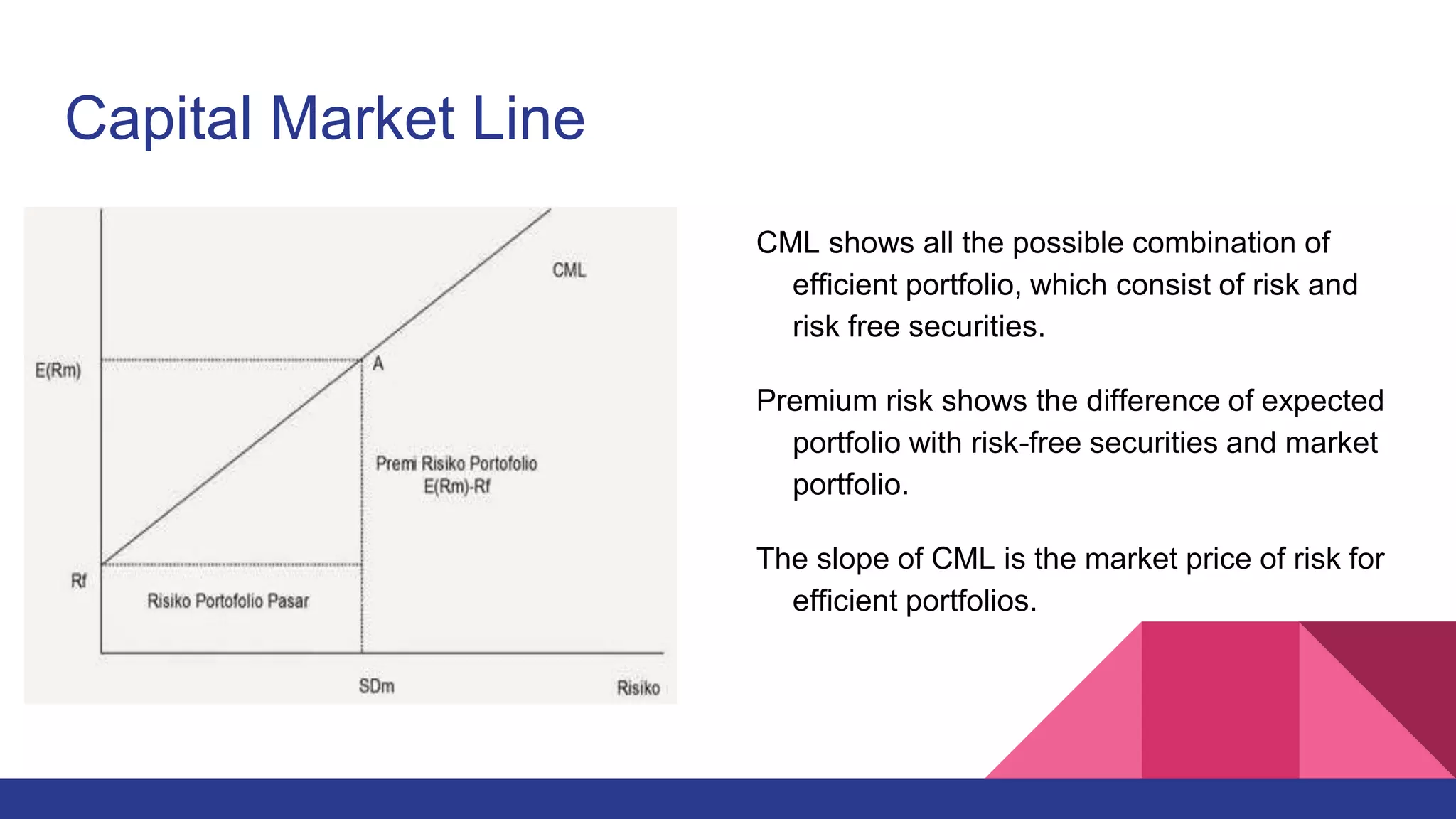
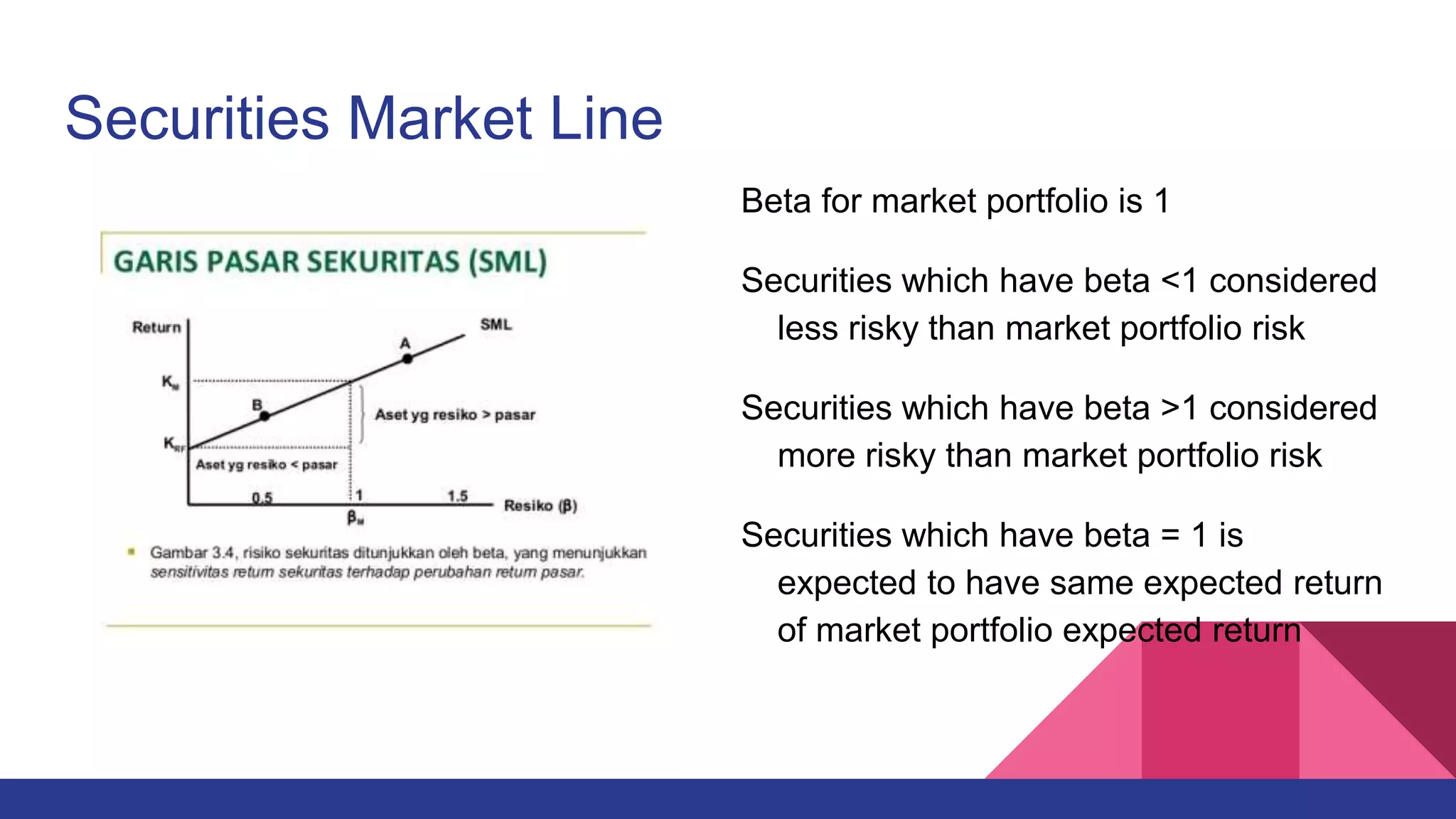
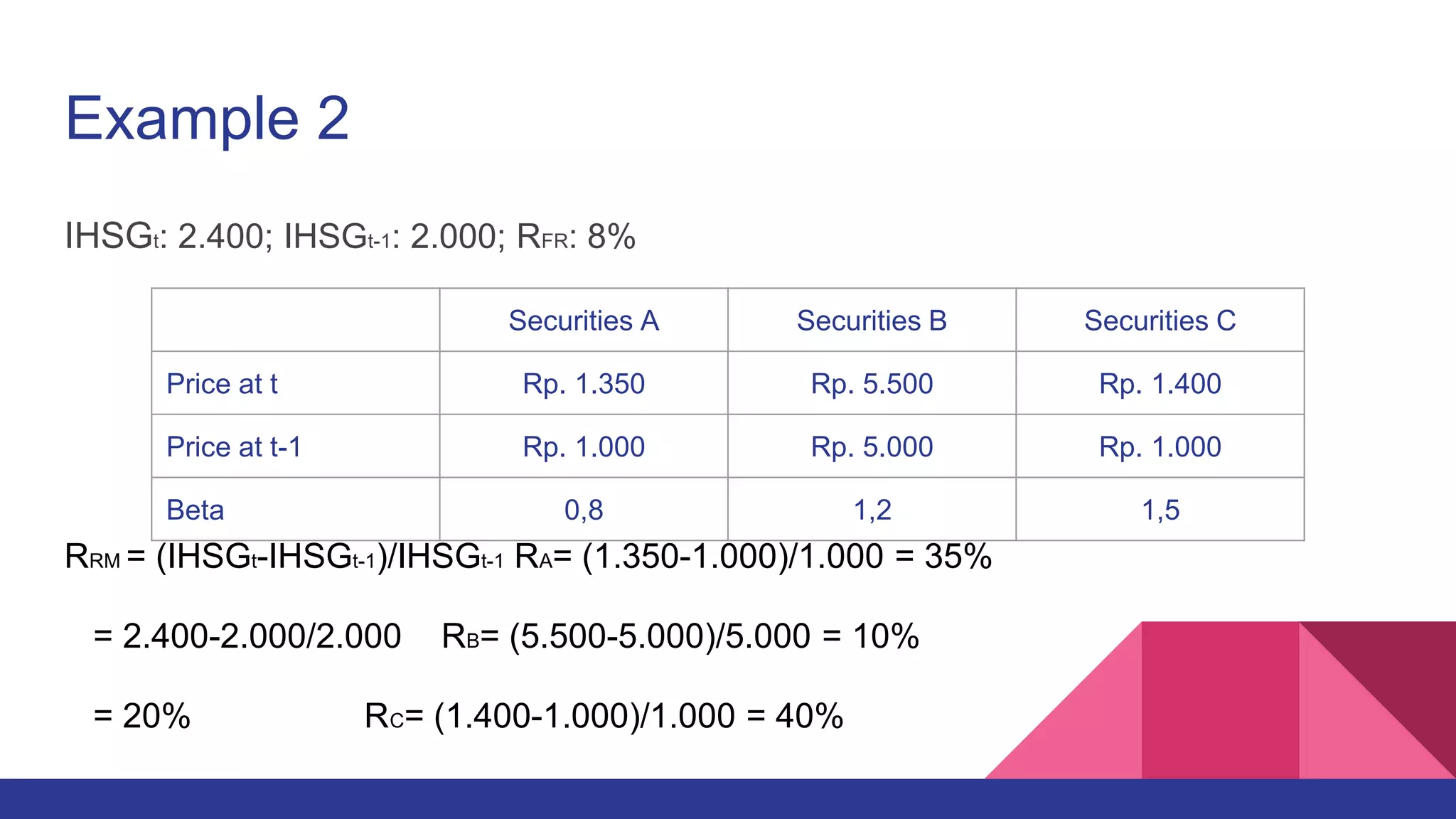
This document provides an overview of the Capital Asset Pricing Model (CAPM). It outlines the key assumptions of CAPM, including that investors aim to maximize returns based on risk. It describes how the capital market reaches equilibrium when there is no incentive to trade. It also defines concepts like the capital market line, securities market line, beta, and the CAPM formula. Examples are provided to demonstrate how to calculate expected returns using CAPM. The document concludes by discussing empirical testing of CAPM and common findings that its assumptions do not always hold in practice.

1. Capital Asset Pricing Model
(CAPM)

2. Assumptions of CAPM
1. All investors aim to maximize economic utilities.
2. All investors make decision based on the return and standard deviation.
3. All investors have Homogenous expectation towards input factors that is used to make
portfolio.
4. All investors can lend and borrow unlimited amount under the risk free rate of return.
5. Short selling is allowed.
6. Securities as highly divisible.
7. All securities are liquid, can be sold at current market price.
8. No transaction fee.

3. Assumptions of CAPM
9. There is no inflation in the market.
10.There is no tax payable for investors.
11. All investors are price-takers
12. The capital market is in equilibrium.

4. Capital Market Equilibrium
Occurs when there is no more incentive for investors to trade.
Assumptions under capital market equilibrium:
1. All investors will choose market portfolio.
2. Market portfolio contained optimized securities, efficient frontier.

5. Market Portfolio
AB curve shows the market portfolio, combination
of risk and risk-free securities.
In equilibrium, all risk securities should be at
market portfolio (M), so the market portfolio is
perfectly diversified.
In practice market portfolio is only contained
securities in one market (i.e. IDX), not all
securities in the world.

6. Capital Market Line
CML shows all the possible combination of
efficient portfolio, which consist of risk and
risk free securities.
Premium risk shows the difference of expected
portfolio with risk-free securities and market
portfolio.
The slope of CML is the market price of risk for
efficient portfolios.

7. Capital Market Line
Equation for Harga pasar dari resiko:

8. Securities Market Line
Depict tradeoff between risk and expected return for efficient portfolio, but not for individual securities
In portfolio, additional expected return happens because of additional risk from portfolio itself
In individual securities, additional expected return is because of additional individual securities risk
which is determined by Beta
Beta determined the amount of additional expected return for individual securities with argument that
for portfolio which is perfectly diversified, non systematic risk is gone
This argument is based on the assumption homogenous expectation (every investor will create
perfectly diversified portfolio. leaving only Beta risk)

9. Securities Market Line
Beta for market portfolio is 1
Securities which have beta <1 considered
less risky than market portfolio risk
Securities which have beta >1 considered
more risky than market portfolio risk
Securities which have beta = 1 is
expected to have same expected return
of market portfolio expected return

10. CAPM Formula
Elton and Gruber (1995) introduce Capital Asset Pricing Model (CAPM)
This formula can be used to calculate the expected return from a portfolio or
individual securities
RBR = Risk Free Rate (RFR)
βi = Beta
E(Rm) = Market Portfolio Expected Return

11. CAPM Example
RFR = 9%;E(Rm) = 13%; βA = 1,3
E(RA) = 9% + (13% - 9%) . 1,3
= 9% + 5,2%
= 14,2%
To check whether the securities are undervalued or overvalued is by comparing the
expected return with the real return

12. Example 2
IHSGt: 2.400; IHSGt-1: 2.000; RFR: 8%
RRM = (IHSGt-IHSGt-1)/IHSGt-1 RA= (1.350-1.000)/1.000 = 35%
= 2.400-2.000/2.000 RB= (5.500-5.000)/5.000 = 10%
= 20% RC= (1.400-1.000)/1.000 = 40%
Securities A Securities B Securities C
Price at t Rp. 1.350 Rp. 5.500 Rp. 1.400
Price at t-1 Rp. 1.000 Rp. 5.000 Rp. 1.000
Beta 0,8 1,2 1,5

13. Example 2(Cont.)
Real Return:
E(RA)= 8% + 0,8 (20%-8%)= 17,6%
E(RB)= 8% + 1,2 (20%-8%)= 22,4%
E(RC)= 8% + 1,5 (20%-8%)= 26,0%
Conclusion:
Securities A= Undervalued; Securities B= Overvalued;
Securities C= Undervalued

14. CAPM Model Explained
Market Portfolio Risk
Contribution of each securities towards market portfolio risk is depends on the
return covariance with the market portfolio

15. BETA CALCULATION
Beta is the covariance return of individual securities

16. CAPM Model Explained (cont.)
Market portfolio risk measured by standard deviation
Security risk contribution towards total portfolio risk contribution can be
considered as a change of portfolio risk due to changes in proportion of the
securities

17. Empirical Testing of CAPM
CAPM Model can be tested if the model has been converted into ex post model
Where:
Ri.t = Return on asset i in period t
RBR.t = Risk Free Rate in period t
βi = Beta
Rm.t = Return on market portfolio in period t
ei.t = Error

18. The difference between Ex ante and Ex post
Ex Ante
Theoretical model
Slope of Securities Market Line (SML) should
be positive
Ex Post
Empirical model
Slope of Securities Market Line (SML) Should
be 0 or negative
E(RM)
E(Ri)
M
RBR
0 1,0
Beta
1,0 Beta
M
RM
0
RBR
Ri

19. Empirical Testing of CAPM (cont.)
Predictions:
Intercept δ0 is expected not differ significantly to 0
Beta is the only factor that explains return of security risk
.
Relationship between Return and Risk should be Linear
δ1 should be positive or the return on market portfolio must be higher than Risk-free Rate of
Return

20. Results of testing the CAPM model
The value of intercept is significantly higher than 0
The coefficient of beta has small value than return on market portfolio minus
Risk-free Rate of Return
The coefficient of beta has positive value / δ1 > 0
Other factors (beside Beta) can explain the portion of securities return
P/E ratio (Basu 1977)
Firm-size (Banz 1981 and Reinganum 1981)
Dividend yield (Rosenberg and Marathe 1977, Litzenberger and Ramaswamy,1979)
Seasonality effect or January effect (Keim,1985)