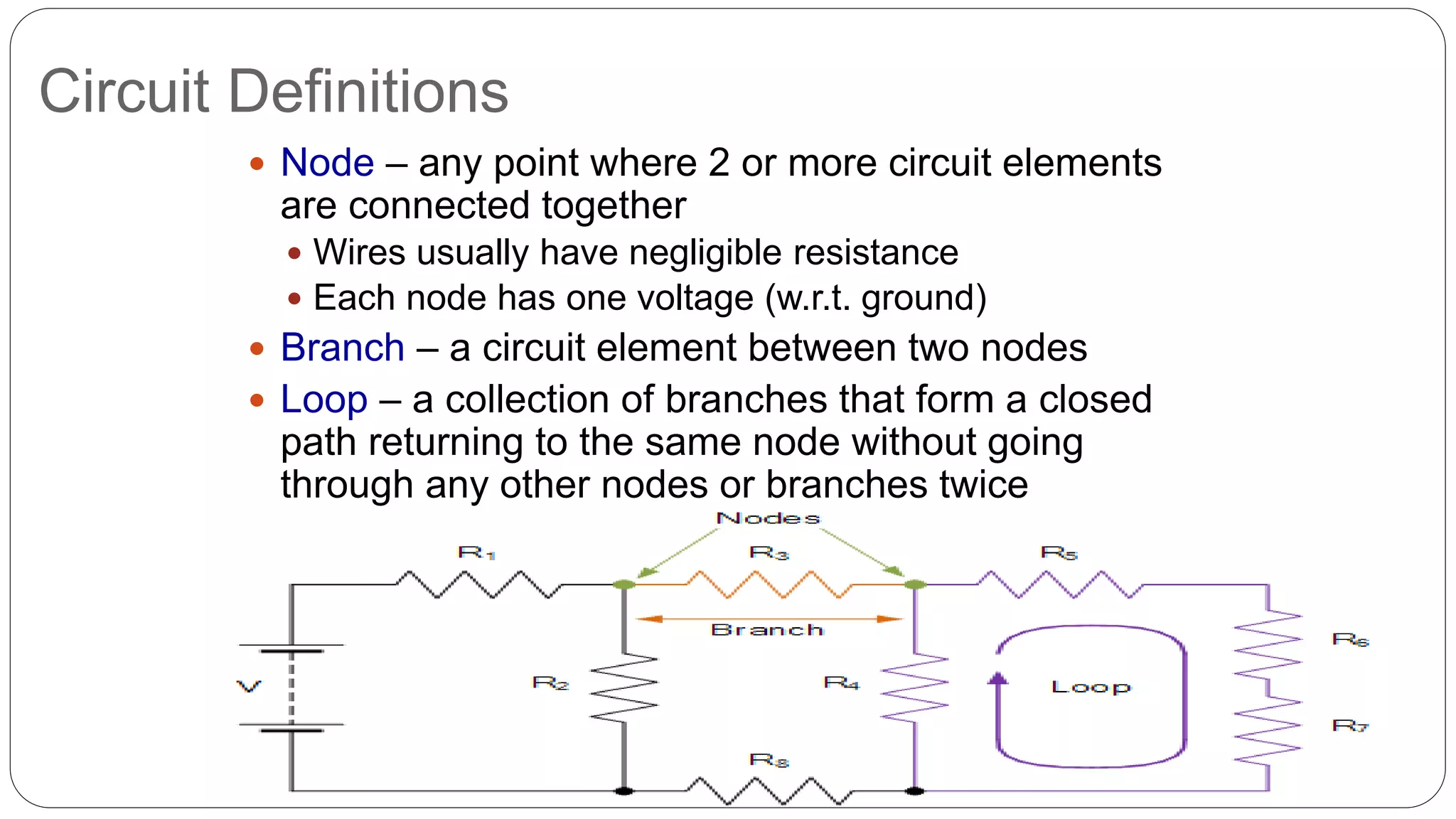
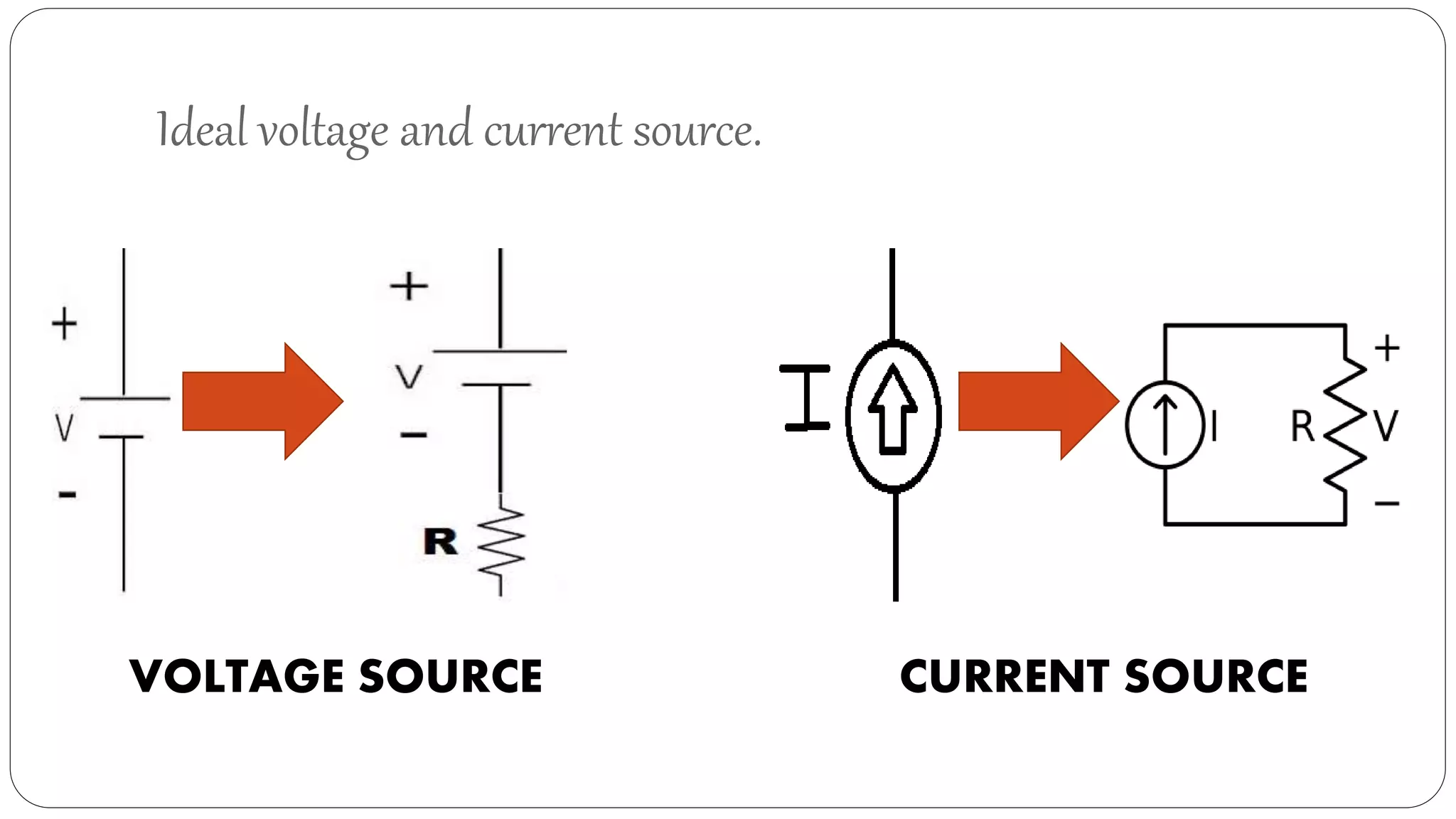
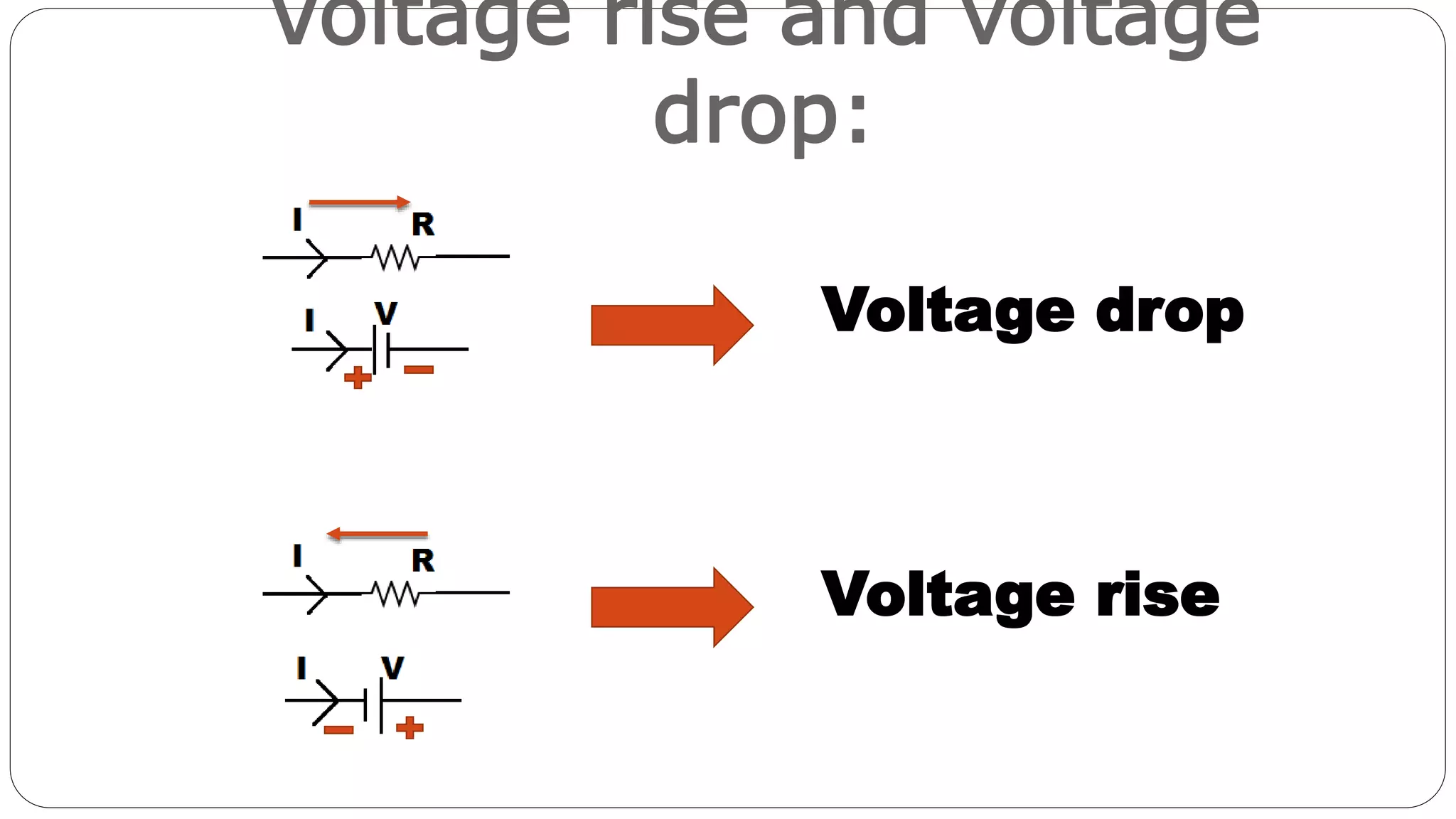
This document discusses Kirchhoff's laws for circuits and networks. It provides examples of applying Kirchhoff's Current Law (KCL) and Kirchhoff's Voltage Law (KVL) to solve for unknown currents and voltages in circuits. KCL states that the algebraic sum of currents at any node is zero. KVL states that the algebraic sum of the voltages around any closed loop is zero. The document also defines related terms like nodes, branches, and loops and shows voltage rises and drops.

1. ACTIVELEARNINGASSIGnMENT
CIRCUITS AND NETWORKS(2130901)
Prepared by
Group - 1
Div- B
Sem-3rd
Branch-Electrical
Guided by: Prof. Megha Ma’m
GANDHINAGAR INSTITUTE OF Technology.

2. Brijesh Patel -140120109030
Kavan Patel -140120109032
Darshil Shah -140120109050
Group : 1
PREPAREDBY:
ENROLLMENTNO.

3. TOPIC NAME:
•KIRCHHOFF’S LAWS.

4. TYPES OF LAWS:
Kirchhoff’s laws.
KIRCHHOFF’S CURRENT LAW(KCL) KIRCHHOFF’S VOLTAGE LAW (KVL)
These laws are first derived by Guatov Robert
Kirchhoff and hence these laws are also referred
as Kirchhoff Laws.

5. Circuit Definitions
 Node – any point where 2 or more circuit elements
are connected together
 Wires usually have negligible resistance
 Each node has one voltage (w.r.t. ground)
 Branch – a circuit element between two nodes
 Loop – a collection of branches that form a closed
path returning to the same node without going
through any other nodes or branches twice

6. Kirchhoff's Current Law
(KCL)
 The algebraic sum of currents entering a node is zero
 Add each branch current entering the node and subtract
each branch current leaving the node
 Σ currents in - Σ currents out = 0
 Or Σ currents in = Σ currents out
(IB + IC + ID) - IA = 0
Then, the sum of all the
currents is zero. This can be
generalized as follows,

7. Kirchhoff's Voltage Law
(KVL)
“The algebraic sum of all voltages around a
closed loop must be equal to zero”.
 Σ voltage drops - Σ voltage rises = 0
 Or Σ voltage drops = Σ voltage rises
That means, V1 + V2 + V3 + ................... + Vm −
Vm + 1 − Vm + 2 − Vm + 3 + .....................− Vn = 0.
So accordingly Kirchhoff Second
Law,
∑V = 0.

8. Ideal voltage and current source.
VOLTAGE SOURCE CURRENT SOURCE

9. Voltage rise and voltage
drop:
Voltage drop
Voltage rise

10. Example.
 Find the current through 8Ω resistor using KIRCHHOFF’S LAWS.

11. EXAMPLE OF KCL

12. EXAMPLE OF KCL
the nodal equations (We assume all currents are leaving the node):
0
7
v102
5
2
2
12
0
2
21
6
v51
1
v121

















k
V
k
V
k
VV
k
VV
k
V
k
V
Rearranging the terms:
Solving the linear equations with the Cramer’s Rule:
100259135
7723110


VV
VV
495.3
485
1695
2748.8
485
4243
1
1695
10035
7710
4243
59100
377
485
5935
310













VV

13. EXAMPLE OF KCL
Currents:
 I1k = = -3.252 mA () I2k = = 2.626 mA ()
 I3k = = 1.928 mA () I4k = = 1.928 mA ()
 I5k = = 0.699 mA () I6k = = 0.625 mA ()

14. EXAMPLE OF KVL

15. EXAMPLE OF KVL
 Junction J1:
I = I1 + I2 (equation 1)
 Junction J2:
I1 + I2 = I (equation 2)

16.  Loop A: (start from the upper left corner and move clockwise)
-I1 x (100 Ω) + 1.5V = 0 (equation 3)
Therefore: I1 = 0.015 A
 Loop B:
-9V – I2 x (200 Ω) + I1 x (100 Ω) = 0 (equation 4)
 Substituting the value of I1 into equation 3 yields:
-9 – I2 x (200 Ω) + (0.015)(100 Ω) = 0
-7.5 = (200) x I2 therefore: I2 = -0.0375 A
 And then I = -0.0225 A
 VR1 = I1 x R1 = (0.015 A) x (100 Ω) therefore VR1 = 1.5V
 VR2 = I2 x R2 = (-0.0375 A) x (200 Ω) therefore VR2 = -7.5V

17. REFERENCES.
www.electricals4u.com
www.eefundamentals.com
www.electricaleasy.com
www.wikipedia.com/KCL,KVL
CIRCUITS & NETWORKS book