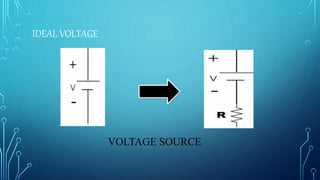
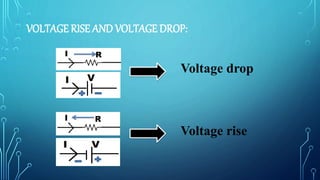
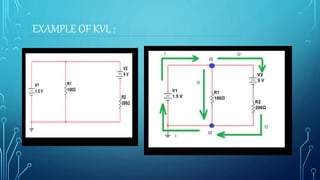
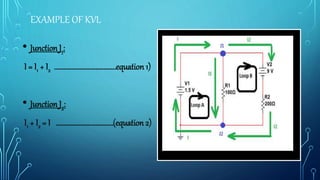
This presentation summarizes Kirchhoff's voltage law (KVL). KVL states that the sum of the voltages around any closed loop in a circuit must be equal to zero. It is one of Kirchhoff's circuit laws derived by Gustav Kirchhoff. KVL can be expressed as the algebraic sum of all the voltage rises and drops around a closed loop equalling zero. An example circuit is provided and KVL is applied to solve for the currents and voltages.

1. PRESENTATION ON
KIRCHHOFF’S VOLTAGE LAW
(KVL)
COURSETITLE : BASICELCTRICALENGINEERING(BEE)
COURSECODE : CSE- 106
SUBMITTEDBY :
NAME : NAFISA ELLAHI
ID : 2016-2-17-006
DEPT : CSE
Submitted to:
DR.AIN-UL-
HUDA

2. TYPES OF LAWS:
Kirchhoff’s laws.
KIRCHHOFF’S CURRENT LAW(KCL) KIRCHHOFF’S VOLTAGE LAW (KVL)
These laws are first derived by Guatov Robert Kirchhoff and hence
these laws are also referred as Kirchhoff Laws.

3. CIRCUIT DEFINITIONS
● Node– any point where 2 or more circuit elements are
connectedtogether
– Wires usually havenegligibleresistance
– Eachnode has one voltage(w.r.t. ground)
● Branch– a circuit element between two nodes
● Loop – a collection of branches that forma closed path
returning to the same node without going through any other
nodes or branches twice

4. KIRCHHOFF'S VOLTAGE LAW (KVL)
•
That means, V1 + V2 + V3 + ................... + Vm − Vm +
1 − Vm + 2 − Vm + 3 + .....................− Vn = 0.
So accordingly Kirchhoff Second Law,
∑V = 0.
“The algebraic sum of all voltages around a closed loop must be
equal to zero”.
Σ voltage drops - Σ voltage rises = 0
Or Σ voltage drops = Σ voltage rises

5. IDEAL VOLTAGE
VOLTAGE SOURCE

6. VOLTAGE RISE AND VOLTAGE DROP:
Voltage drop
Voltage rise

7. EXAMPLE OF KVL :

8. EXAMPLE OF KVL
• Junction J1:
I = I1 + I2 …………………………………equation 1)
• Junction J2:
I1 + I2 = I ………………………………(equation 2)

9. •Loop A: (start from the upper left corner and move
clockwise)
-I1 x (100 Ω) + 1.5V = 0 …………………………………………. (equation 3)
Therefore: I1 = 0.015 A
• Loop B:
-9V – I2 x (200 Ω) + I1 x (100 Ω) = 0 ………………….....(equation 4)

10. • Substituting the value of I1 into (equation 3 )yields:
-9 – I2 x (200 Ω) + (0.015)(100 Ω) = 0
-7.5 = (200) x I2 therefore: I2 = -0.0375 A
•And then I = -0.0225 A
•VR1 = I1 x R1 = (0.015 A) x (100 Ω) therefore VR1 = 1.5V
•VR2 = I2 x R2 = (-0.0375 A) x (200 Ω) therefore VR2 = -7.5V

11. Thanks For
Watching