Introduction to Artificial Intelligence...pptx

Ms. Mayuri Shelke
Artificial Intelligence for Big Data
Mining

Introduction to Artificial
Intelligence

WHAT IS A.I.?
INTELLIGENCE : “The capacity to learn
and solve problems”
ARTIFICIAL INTELLIGENCE : Simulation
of human intelligence by machines

WHAT IS A.I.?
• Artificial intelligence or AI simply means
software used by computers to mimic
aspects of human intelligence.
• Artificial intelligence is a theory and
development of computer systems that can
perform tasks that normally require human
intelligence.
• It can be used as a platform to develop
intelligent systems that are capable of
learning.

Automate the things.
To keep track of data.
To make machines smarter so that they can execute
faster and more
Handle large amount of data in efficient
way.
NEED OF A.I.

ADVANTAGES OF A.I.
• The chances of error are almost nil
• It can be used to explore space, depths of ocean
• It can be used in time consuming tasks
• Machines do not require to sleep or break and are able to function without stopping
DISADVANTAGES OF A.I.
• High cost
• Decrease in demand for human labour
• The storage and access are not as effective as human brains

Healthcare
Gaming
Social
Media
Entertainmen
t
Education
Applications of A.I.…

GENERAL A.I. AGENTS WITH PLATFORMS

WHAT WILL THE NEXT DECADE BRING?
• Improved speech, voice ,image, video recognition will change the way
interact with our devices
• More and more systems will run autonomously in a point.

What is logic programming?
• Logic programming is a programming paradigm that sees computation as automatic
reasoning over a database of knowledge made of facts and rules.
• Basically it means it is a particular way to approach programming.
• The concept of programming arises owing to the need to classify programming languages.
• It refers to the way computer programs solve problems through code.
• Some programming are primarily concerned with implications or the sequence of
operations used to achieve the result.

• Imperative: This uses statements to change a program's state, thus allowing for side effects.
• Functional: This treats computation as an evaluation of mathematical functions and does not
allow changing states or mutable data.
• Declarative: This is a way of programming where you write your programs by describing what
you want to do.
• Object Oriented: This groups the code within the program in such a way that each object is
responsible for itself.
• Procedural: This groups the code into functions and each function is responsible for a
particular series of steps.
• Symbolic: This uses a particular style of syntax and grammar through which the program can
modify its own components by treating them as plain data.
• Logic: This views computation as automatic reasoning over a database of knowledge consisting
of facts and rules.

Understanding the building blocks of logic programming.
• This is a powerful way of approaching the variable matching problem.
• The process of matching variables with different items is called unification.
• This is one of the places logic programming really stands apart. We need to specify something called
relations in logic programming.
• These relations are defined by means of clauses called facts and rules.
• Rules are the things we have learned about how to express various facts and how to query them.
• They are the constraints that we have to work with and they allow us to make conclusions about the
problem domain.

Logic Programming
• Logic Programming is the combination of two words, logic and
programming.
• Logic Programming is a programming paradigm in which the problems
are expressed as facts and rules by program statements but within a
system of formal logic.
13

How to Solve ?
• Logic programming looks for solutions by using facts and rules. We
need to specify a goal for each program.
• Facts->Concrete relations among objects.
• Rules->A pattern of relationships among the database objects.
14

How to Solve ?
• When we write a program in the logic programming
paradigm, we specify a set of statements based on facts
and rules about the problem domain and the solver
solves it using this information.
• Predicates are used to build atomic formulas or atoms,
which state true facts. Predicates and atoms are used to
create formulas and perform queries.
• Logic languages most often rely on queries in order to
display relevant data. These queries can exist as part of
machine learning, which can be run without the need for
manual intervention.
15

How to Solve?
• In the case where a logic program and a goal don't contain any
variables, the solver comes up with a tree that constitutes the
search space for solving the problem and getting to the goal.
• One of the most important things about logic programming is how
we treat the rules. Rules can be viewed as logical statements.
E.g. : 1)Horror movies, English => James Wan
•It can be read as the implication If you like Horror movies in English,
then you would like movies made by James Wan.
2)Grandfather(X,Y):- Father(X,Z),Parent(Z,Y)
• This implies that for X to be the grandfather of Y, Z should be a
parent of Y and X should be father of Z.
•This construction is used in various forms throughout logic
programming to solve various types of problems.
16

Installing Python Packages
You can also install the packages directly into Pycharm IDE as shown
below.

Installing Python Packages
• SymPy is an open-source Python library for symbolic computation. It
provides computer algebra capabilities either as a standalone
application, as a library to other applications.
• LogPy is a library for logic and relational programming in Python. LogPy
enables the expression of relations and the search for values which
satisfy them.

Matching Mathematical Expressions
• In mathematics, an expression or mathematical expression is a finite
combination of symbols that is well-formed according to rules that
depend on the context.
• An example of a mathematical expression with a variable is 2x + 3.
• In logic programming, we find a way to compare these expressions and
find out the unknown values.

• Create a new Python file and import the following packages:
from logpy import run, var, fact
import logpy.assoccomm as la
• Define a couple of mathematical operations:
add = 'addition'
mul = 'multiplication'

Both addition and multiplication are commutative operations. Let's
specify that:
fact(la.commutative, mul)
fact(la.commutative, add)
fact(la.associative, mul)
fact(la.associative, add)
Let's define some variables:
a, b, c = var('a'), var('b'), var('c')

Consider the following expression:
expression_og = 3 x (-2) + (1 + 2 x 3) x (-1)
The first expression would be:
expression1 = (1 + 2 x a) x b + 3 x c
The second expression would be:
expression2 = c x 3 + b x (2 x a + 1)

If you observe carefully, all three expressions represent the same
basic expression. Our goal is to match these expressions with the
original expression to extract the unknown values:
expression_og = (add, (mul, 3, -2), (mul, (add, 1, (mul, 2, 3)), -1))
….[ 3 x (-2) + (1 + 2 x 3) x (-1) ]
expression1 = (add, (mul, (add, 1, (mul, 2, a)), b), (mul, 3, c))
….[ (1 + 2 x a) x b + 3 x c ]
expression2 = (add, (mul, c, 3), (mul, b, (add, (mul, 2, a), 1)))
….[ c x 3 + b x (2 x a + 1) ]

Compare the expressions with the original expression. The method run is commonly used
in logpy. This method takes the input arguments and runs the expression. The first
argument is the number of values, the second argument is a variable, and the third
argument is a function:
print(run(0, (a, b, c), la.eq_assoccomm(expression1, expression_og)))
print(run(0, (a, b, c), la.eq_assoccomm(expression2, expression_og)))
You will see the following output on your Terminal:
((3, -1, -2),)
((3, -1, -2),)

Validating Primes
• We all know what prime numbers are.
• In fact, that's part of what makes primes so interesting: not only is the
number line studded with primes all the way up to infinity, but that
whole number line can be produced using nothing but primes. This is
why primes are so relevant in certain fields — primes have very special
properties for factorization.

Validating Primes
Create a new Python file and import the following packages:
import itertools as it
import logpy.core as lc
from sympy.ntheory.generate import prime, isprime
Method 1 : Check if the elements of x are prime
# def check_prime(x):
if lc.isvar(x):
return lc.condeseq([(lc.eq, x, p)] for p in map(prime, it.count(1)))
else:
return lc.success if isprime(x) else lc.fail
x = lc.var()

Validating Primes
Method 2 : Check if an element in the list is a prime number
list_nums = (23, 4, 27, 17, 13, 10, 21, 29, 3, 32, 11, 19)
print('n List of primes in the list: ')
print(set(lc.run(0, x, (lc.membero, x, list_nums), (check_prime, x))))
The method membero checks if a given number is a member of
the list of numbers specified in the input argument

Validating Primes
Method 3 : Print prime numbers serially
print('nList of first 7 prime numbers:')
print(lc.run(7, x, check_prime(x)))
List of primes in the list: (3, 11, 13, 17, 19, 23, 29)
List of first 7 prime numbers: (2, 3, 5, 7, 11, 13, 17)

Validating Primes
• Primes are important because the security of many encryption
algorithms are based on the fact that it is very fast to multiply two large
prime numbers and get the result, while it is extremely computer-
intensive to do the reverse.
• This is also the reason why prime numbers are used to calculate hash-
codes – because they are co-prime with the maximum number of
integers. A correct and fast algorithm to check whether a number is
prime has been seeked for a long time by mathematicians and
computer scientists.

What is Heuristic?
● A rule of thumb that helps us narrow down the search by eliminating the options that are
obviously wrong.
● Adapt the approach to a problem based on previous solutions to similar problems.
● Provides approximate solution in reasonable time.
● A good heuristic is optimistic.

Heuristic Search
A searching technique that looks to find a solution
that may or may not be optimal, but is sufficient
in a given limited time frame.

Need of Heuristics
● Ease in decision making.
● Simplify complex questions
● Help speed up the process.
● Help with problem solving.

Terminologies & Properties
● Rational/Problem-Solving Agent
● Search Space
● Start State and Goal Test
● Search Tree
● Completeness
● Optimality
● Complexity
Search Algorithms

Informed Search
● Requires domain knowledge for efficient searching.
● Makes use of heuristic function.
● Accuracy trade-off for speed and time
● Good Solution is accepted
● It may or may not be complete .
● It is comparatively more efficient.
● Can handle large search problems
● Also known as heuristic search
● Example: Greedy Search, A* Search, Graph Search

Uninformed Search
● Doesn’t require domain knowledge to perform searching.
● Operates in a brute-force way.
● Speed and time trade-off for Accuracy.
● Optimal Solution can be achieved
● It is always complete.
● It is comparatively less efficient.
● Impractical to handle large search problems
● Also known as blind search
● Example: Breadth-first search, Uniform Cost search

Local Search Techniques
• Search algorithms like DFS or BFS explore all the search space
systematically by keeping one or more paths in memory and by recording
which alternatives have been explored.
• When a goal is found, the path to that goal constitutes a solution.
• There are some problems where path is irrevelevant eg:8 Queens
• Local search algorithms can be very helpful if we are interested in the
solution state but not in the path to that goal.
• Local search algorithm is a heuristic search algorithm.

Optimization
• Local search is often suitable for optimization problems.
• Local search algorithm works for pure optimized problems. A
pure optimization problem is one where all the nodes can give
a solution. But the target is to find the best state out of all
according to the objective function.
• Search for best state by optimizing an objective function.
WHAT IS OBJECTIVE FUNCTION?
An objective function is a function whose value is either
minimized or maximized in different contexts of the optimization
problems

Local Search Techniques
ADVANTAGES:
• They use very little memory
• They can find reasonable solutions in large or infinite (continuous) state
spaces.
EXAMPLES :
• Hill-climbing
• Simulated annealing
• Tabu Search

Hill Climbing Algorithm
• Hill climbing is a popular local search technique, it is also called greedy local search.
• It is a loop that continuously moves towards the increasing value and terminates
when peak is reached. This value can be objective function/ heuristic function .
• The heuristic function measures the difference between the current state and the
goal.
• When we start, it checks if the state is the final goal. If it is, then it stops. If not, then
it selects an update and generates a new state. If it's closer to the goal than the
current state, then it makes that the current state. If not, it ignores it and continues
the process until it checks all possible updates. It basically climbs the hill until it
reaches the summit
• It does not look ahead of its immediate neighbours.
“Like climbing Everest in thick fog with amnesia”

STATE SPACE LANDSCAPE OF SEARCH
Hence we can say that,
Hill Climbing gets stuck at local optima depending on the position from where we start.

Drawbacks of Hill Climbing
• LOCAL MAXIMA
• PLATEAUS
• DIAGONAL RIDGES

SIMULATED ANNEALING
WHAT IS ANNEALING?
• Annealing is a thermal process for obtaining low energy states
of a solid in a heat bath.
• The process contains two steps:
• Increase the temperature of the heat bath to a maximum value at
which the solid melts.
• Decrease carefully the temperature of the heat bath until the
particles arrange themselves in the ground state of the solid. Ground
state is a minimum energy state of the solid
• The rate of cooling is important because it directly impacts the
final result.

Simulated Annealing
• Simulated Annealing is a variation of the hill climbing
technique, however this it allows us to take a downhill move.
• Idea:
1.The search is started with a randomized state.
2.Calculate the objective function. Say the change in objective function
is d ;
3.If d is positive, then move to that state . If it’s worse then take it with
some probability proportional to the temperature and the delta
between the new and old states.
4.As time passes, decrease the temperature slowly, accepting less bad
moves at each temperature level until at very low temperatures the
algorithm becomes a greedy hill-climbing algorithm.

Simulated Annealing
• With simulated annealing, a system changes its state from the
original state Sold to a new state Snew with a probability given as:
P= 1/(1+exp(-ΔE/T))
Where, ΔE= Eold – Enew (Energy change) and T is the non-negative
parameter and acts like temperature parameter in physical
system.
• High T: probability of “locally bad” move is higher
• Low T: probability of “locally bad” move is lower
Analogy Used
Physical System Optimization Problem
State(Configuration) Solution
Energy Cost Function
Ground state Optimal Solution
Temperature Control Parameter

Advantages
• It can find global maxima even after finding local maxima
• Statistically guarantees finding an optimal solution
• Is relatively easy to code, even for complex problems
Disadvantages
• In practice, the convergence of the algorithm depends of
the cooling schedule.Can take a long time to run if the
schedule is very long
• There are a lot of tuneable parameters in this algorithm

Applications
Travelling Salesman Problem
• Graph partitioning
• Graph coloring
• Image processing
• VLSI Design
• Placement
• Routing
• Array logic minimization
• Layout
• Facilities layout

1. Construct a string using greedy search
47
What is Greedy Search?
A heuristic searching technique that chooses
the best possible answer in each step till it
reaches the end . Without regarding the
overall solution.

Algorithm
48
● To recreate the input string based on the alphabets.
● Store all the alphabets of the language in a string
● Accept the target string from user
● Use the Simpleai search package and Search Problem library
● Compute the result by concatenating the current string and the output of the
action that needs to be taken.
● Define a Heuristic to calculate how far we are from the goal and use that as
the heuristic to guide it towards the goal
● Finally run the solver that would return the string after each iteration

Applications
49
● CPU Scheduling algorithms.
● Minimum spanning trees.
● Dijkstra shortest path algorithm.
● Travelling salesman problem

2. Solving a problem with constraints
50
What are constraints ?
A constraint satisfaction problem (CSP) is a
problem that requires its solution to be
within some limitations or conditions, also
known as constraints, consisting of a finite
variable set, a domain set and a finite
constraint set.

Examples
51
● Define the constraint that
specifies that if the first variable
is odd, then the second variable
should be even
● The n-Queen problem: The
local condition is that no two
queens attack each other, i.e.
are on the same row, or
column, or diagonal.

3.Solving the region coloring problem
52
Definition
We have a few regions in the diagram that
are labeled with names. Our aim being
coloring with four colors so that no
adjacent regions have the same color.
(Constraint Satisfaction Framework)

Algorithm
53
● Define the list of possible colors
● Define the constraints by their adjacent nodes
● Use the variables to initialize the objects
● Thereafter solve the problem using the backtracking
solution

Applications
55
● Making Timetables
● Map Coloring
● Checking Bipartite graphs
● Mobile radio frequency assignment

Introduction
• The 8-puzzle problem is a puzzle invented and popularized by Noyes Palmer
Chapman in the 1870s.
• It is played on a 3-by-3 grid with 8 square blocks labeled 1 through 8 and a
blank square.
• The goal is to rearrange the blocks so that they are in order.
• You are permitted to slide blocks horizontally or vertically into the blank
square.
• Example:
1 2 3
4 6
7 5 8
1 2 3
4 5 6
7 8
Initial State Final State

Techniques
• The 8-puzzle problem can be solved using two techniques:
A. Uninformed Search (Without Heuristic)
B. Informed Search (With Heuristic)

Uninformed Search
• This method is also called as Blind Search.
• It uses Breadth First Search (BFS).
• It reaches final state without using Heuristic approach.
• It explores each path before reaching the final state.
• Possible moves: Up, Down, Right, Left.

Uninformed Search
• Example:
1 2 3
4 6
7 5 8
1 2 3
4 5 6
7 8
1 2 3
4 6
7 5 8
2 3
1 4 6
7 5 8
1 2 3
7 4 6
5 8
1 3
4 2 6
7 5 8
1 2 3
4 5 6
7 8
1 2 3
4 6
7 5 8
Initial State Final State
Right
Up Dow
n
Up
Dow
n
Right

Informed Search
• This method uses Heuristic Search to find the solution as early as possible.
• Heuristic search uses Heuristic value for optimizing the search.
• A* algorithm is an example of Informed search algorithms which can be used to
solve 8-puzzle problem.

A* Algorithm
• A* algorithm is one of the best and popular technique used in path finding and
graph traversal.
• It starts with the initial node and chooses the next node based on its f-score.
f(n) = h(n) + g(n)
where h(n) 🡪 no. of misplaced tiles
g(n) 🡪 no. of nodes traversed from start node to current node.

A* Algorithm
• Example:
1 2 3
4 6
7 5 8
1 2 3
4 5 6
7 8
2 3
1 4 6
7 5 8
1 2 3
4 6
7 5 8
1 2 3
7 4 6
5 8
1 2 3
4 5 6
7 8
1 2 3
4 6
7 5 8
1 3
4 2 6
7 5 8
Initial State
g=0, h=3,
f=0+3=3
Final State
g=2, h=3,
f=5
g=1, h=2,
f=2+1=3
g=1, h=4,
f=4+1=5
g=2, h=1,
f=3
g=2, h=3,
f=5
g=1, h=4,
f=4+1=5
1 2 3
4 5 6
7 8
1 2 3
4 5 6
7 8
g=3, h=2,
f=5
g=3, h=0,
f=3

Conclusion
• Learnt about Heuristic and non-heuristic techniques for solving
8-puzzle problem.
• Heuristic method is more suitable as it reduces the execution
time and provides solution as early as possible.
• Used A* algorithm to solve 8-puzzle problem.

INTRODUCTION
● Genetic Algorithm (GA) is a search-based optimization technique
based on the principles of Genetics and Natural Selection.
● It is frequently used to find optimal or near-optimal solutions to
difficult problems which otherwise would take a lifetime to
solve.
● It is frequently used to solve optimization problems, in research,
and in machine learning.

Introduction to Optimization
Optimization is the process of making something better. In any process, we have a
set of inputs and a set of outputs as shown in the following figure.
The aim of optimization is to find that point or set of points in the search space.

Understanding evolutionary and genetic algorithms
Genetic algorithm is a type of evolutionary algorithm. So, in order to
understand genetic algorithms, we need to discuss evolutionary
algorithms.
An evolutionary algorithm is a meta heuristic optimization algorithm that
applies the principles of evolution to solve problems.
The concept of evolution is similar to the one we find in nature.

What are Genetic Algorithms?
GAs were developed by John Holland and his students and colleagues
at the University of Michigan, most notably David E. Goldberg and
has since been tried on various optimization problems with a high
degree of success.
Genetic Algorithms are sufficiently randomized in nature, but they
perform much better than random local search (in which we just try
various random solutions, keeping track of the best so far), as they
exploit historical information as well.

It is a subset of evolutionary algorithm:
● Ant Colony optimization
● Swarm Particle Optimization
Models biological processes:
Genetics Evolution To optimize highly complex objective functions:
● Very difficult to model mathematically
● NP-Hard (also called combinatorial optimization) problems (which
are computationally very expensive)
● Involves large number of parameters (discrete and/or continuous)
Genetic Algorithm

Advantages of GAs
GAs have various advantages which have made them immensely popular. These
include −
● Does not require any derivative information (which may not be available for
many real-world problems).
● Is faster and more efficient as compared to the traditional methods.
● Has very good parallel capabilities.
● Optimizes both continuous and discrete functions and also multi-objective
problems.
● Provides a list of “good” solutions and not just a single solution.
● Always gets an answer to the problem, which gets better over the time.
● Useful when the search space is very large and there are a large number of
parameters involved.

Limitations of GAs
Like any technique, GAs also suffer from a few limitations. These include −
● GAs are not suited for all problems, especially problems which are
simple and for which derivative information is available.
● Fitness value is calculated repeatedly which might be computationally
expensive for some problems.
● Being stochastic, there are no guarantees on the optimality or the
quality of the solution.
● If not implemented properly, the GA may not converge to the optimal
solution.

Why GAs?
Genetic Algorithms have the ability to deliver a “good-enough”
solution “fast-enough”. This makes genetic algorithms attractive for
use in solving optimization problems. The reasons why GAs are
needed are as follows −
● Solving Difficult Problems
● Failure of Gradient Based Methods
● Getting a Good Solution Fast

Basic Terminology
Before beginning a discussion on Genetic Algorithms, it is essential to be
familiar with some basic terminology which will be used throughout this
tutorial.
● Population − It is a subset of all the possible (encoded) solutions to the
given problem. The population for a GA is analogous to the population
for human beings except that instead of human beings, we have
Candidate Solutions representing human beings.
● Chromosomes − A chromosome is one such solution to the given
problem.
● Gene − A gene is one element position of a chromosome.
● Allele − It is the value a gene takes for a particular chromosome.

● Genotype − Genotype is the population in the computation space. In the
computation space, the solutions are represented in a way which can be easily
understood and manipulated using a computing system.
● Phenotype − Phenotype is the population in the actual real world solution space
in which solutions are represented in a way they are represented in real world
situations.
● Decoding and Encoding − For simple problems, the phenotype and genotype
spaces are the same. However, in most of the cases, the phenotype and
genotype spaces are different. Decoding is a process of transforming a solution
from the genotype to the phenotype space, while encoding is a process of
transforming from the phenotype to genotype space. Decoding should be fast as
it is carried out repeatedly in a GA during the fitness value calculation.
● Fitness Function − A fitness function simply defined is a function which takes the
solution as input and produces the suitability of the solution as the output. In
some cases, the fitness function and the objective function may be the same,
while in others it might be different based on the problem.
● Genetic Operators − These alter the genetic composition of the offspring. These
include crossover, mutation, selection, etc.

GA implementation involved
with the realization of the
following operations:
1. Encoding: How to represent a solution to fit with GA framework.
2. Convergence: How to decide the termination criterion.
3. Mating pool: How to generate next solutions.
4. Fitness Evaluation: How to evaluate a solution.
5. Crossover: How to make the diverse set of next solutions.
6. Mutation: To explore other solution(s).
7. Inversion: To move from one optima to other

Basic Structure
The basic structure of a GA is as follows −
We start with an initial population (which may be generated at random or seeded by
other heuristics), select parents from this population for mating.
Apply crossover and mutation operators on the parents to generate new off-springs.
And finally these off-springs replace the existing individuals in the population and
the process repeats. In this way genetic algorithms actually try to mimic the human
evolution to some extent.

Flow chart of the
working of Genetic
Algorithm

Framework of Genetic Algorithms:

A generalized pseudo-code for a GA is explained in the following
program −
GA()
initialize population
find fitness of population
while (termination criteria is reached) do
parent selection
crossover with probability pc
mutation with probability pm
decode and fitness calculation
survivor selection
find best
return best

GA Based Machine Learning
Genetic Algorithms also find application in Machine Learning. Classifier systems are a
form of genetics-based machine learning (GBML) system that are frequently used in the
field of machine learning. GBML methods are a niche approach to machine learning.
There are two categories of GBML systems −
● The Pittsburg Approach − In this approach, one chromosome encoded one
solution, and so fitness is assigned to solutions.
● The Michigan Approach − one solution is typically represented by many
chromosomes and so fitness is assigned to partial solutions.
It should be kept in mind that the standard issue like crossover, mutation, Lamarckian
or Darwinian, etc. are also present in the GBML systems.

Genetic Algorithms - Application Areas
Below is the list of some areas in which Genetic Algorithms are frequently used :
● Optimization − Genetic Algorithms are most commonly used in optimization
problems wherein we have to maximize or minimize a given objective function
value under a given set of constraints. The approach to solve Optimization
problems has been highlighted throughout the tutorial.
● Economics − GAs are also used to characterize various economic models like the
cobweb model, game theory equilibrium resolution, asset pricing, etc.
● Neural Networks − GAs are also used to train neural networks, particularly
recurrent neural networks.
● Parallelization − GAs also have very good parallel capabilities, and prove to be
very effective means in solving certain problems, and also provide a good area
for research.

● Image Processing − GAs are used for various digital image processing (DIP) tasks
as well like dense pixel matching.
● Vehicle routing problems − With multiple soft time windows, multiple depots
and a heterogeneous fleet.
● Scheduling applications − GAs are used to solve various scheduling problems as
well, particularly the time-tabling problem.
● Machine Learning − as already discussed, genetics based machine learning
(GBML) is a niche area in machine learning.
● Robot Trajectory Generation − GAs have been used to plan the path which a
robot arm takes by moving from one point to another.
● Parametric Design of Aircraft − GAs have been used to design aircrafts by
varying the parameters and evolving better solutions.

● DNA Analysis − GAs have been used to determine the structure of DNA
using spectrometric data about the sample.
● Multimodal Optimization − GAs are obviously very good approaches for
multimodal optimization in which we have to find multiple optimum
solutions.
● Traveling salesman problem and its applications − GAs have been used to
solve the TSP, which is a well-known combinatorial problem using novel
crossover and packing strategies.

Genetic Algorithm
• A genetic algorithm is an evolutionary algorithm
where we use a heuristic to find a string of bits that
solves a problem.
• We continuously iterate on a population to arrive at a
solution.
• We do this by generating new populations containing
stronger individuals.
• We apply probabilistic operators such as selection,
crossover, and mutation in order to generate the next
generation of individuals.
• The individuals are basically strings, where every
string is the encoded version of a potential solution.

Deap Library (Distributed
Evolutionary Algorithms in Python)
⮚Distributed Evolutionary Algorithms in Python (DEAP)
is an evolutionary computation framework for
rapid prototyping and testing of ideas.
⮚It incorporates the data structures and tools required to
implement most common evolutionary computation
techniques such as genetic algorithm, genetic
programming, evolution strategies etc.
⮚Installation through command prompt:
$ pip3 install deap
$ python3
>>> import deap

One Max Problem using Deap library
❑Create a new python file and import the following
import random from deap
import base, creator, tools
❑Let's say we want to generate a bit pattern of length 75,
and we want it to contain 45 ones. We need to define an
evaluation function that can be used to target this
objective:
# Evaluation function
def eval_func(individual):
target_sum = 45
return len(individual) - abs(sum(individual)
- target_sum)

⮚ We now need to define a function to create the toolbox.
Let's define a creator object for the fitness function and to keep track of the individuals.
The Fitness class used here is an abstract class and it needs the weights attribute to be
defined.
⮚ We are building a maximizing fitness using positive weights:
# Create the toolbox with the right parameters
def create_toolbox(num_bits):
creator.create("FitnessMax", base.Fitness, weights=(1.0,))
creator.create("Individual", list, fitness=creator.FitnessMax)
⮚ The first line creates a single objective maximizing fitness named FitnessMax.
⮚ The second line deals with producing the individual.
⮚ In a given process, the first individual that is created is a list of floats. In order to
produce this individual, we must create an Individual class using the creator.
The fitness attribute will use FitnessMax defined earlier.
# Initialize the toolbox
toolbox = base.Toolbox()
Creating toolbox

Registering functions to toolbox
⮚Register Random number generator:
# Generate attributes
toolbox.register("attr_bool", random.randint, 0, 1)
⮚Register individual function:
# Initialize structures
toolbox.register("individual", tools.initRepeat, creator.Individual,
toolbox.attr_bool, num_bits)
⮚Register the Population function:
# Define the population to be a list of individuals
toolbox.register("population",
tools.initRepeat, list, toolbox.individual)

⮚ Register the evaluation function i.e. the fitness function:
# Register the evaluation operator
toolbox.register("evaluate", eval_func)
⮚ Register the crossover operator: (using cxTwoPoint method)
# Register the crossover operator
toolbox.register("mate", tools.cxTwoPoint)
⮚ Register the mutation operator: (using mutFlipBit)
# Register a mutation operator
toolbox.register("mutate", tools.mutFlipBit, indpb=0.05)
⮚ Register the selection operator: (using selTournament)
# Operator for selecting individuals for breeding
toolbox.register("select", tools.selTournament, tournsize=3)
return toolbox

if __name__ == "__main__":
# Define the number of bits
num_bits = 75
# Create a toolbox using the above parameter
toolbox = create_toolbox(num_bits)
# Seed the random number generator
random.seed(7)
# Create an initial population of 500 individuals
population = toolbox.population(n=500)
# Define probabilities of crossing and mutating
probab_crossing, probab_mutating = 0.5, 0.2
# Define the number of generations
num_generations = 60
# Evaluate all the individuals in the population using the fitness functions:
print('nStarting the evolution process’)
# Evaluate the entire population
fitnesses = list(map(toolbox.evaluate, population))
for ind, fit in zip(population, fitnesses):
ind.fitness.values = fit
print('nEvaluated', len(population), 'individuals’)
# Iterate through generations
for g in range(num_generations):
print("n===== Generation", g)
Implementation of All the Concepts
parameters
num_bits = 75
Population size= 500
No of generations= 60
Max. no. of ones= 45

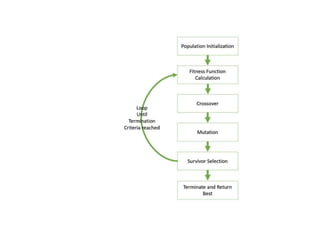
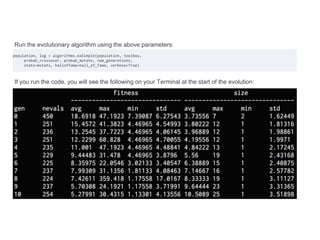
# Select the next generation individuals
offspring = toolbox.select(population, len(population))
# Clone the selected individuals
offspring = list(map(toolbox.clone, offspring))
# Apply crossover and mutation on the offspring
for child1, child2 in zip(offspring[::2], offspring[1::2]):
# Cross two individuals
if random.random() < probab_crossing:
toolbox.mate(child1, child2)
# "Forget" the fitness values of the children
del child1.fitness.values
del child2.fitness.values
# Apply mutation
for mutant in offspring:
# Mutate an individual
if random.random() < probab_mutating:
toolbox.mutate(mutant)
del mutant.fitness.values

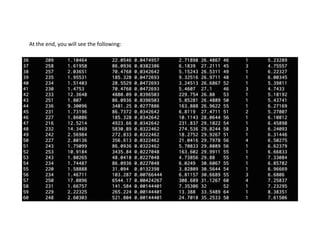
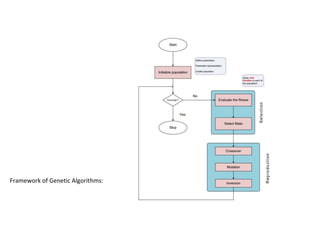
# Evaluate the individuals with an invalid fitness
invalid_ind = [ind for ind in offspring if not ind.fitness.valid]
fitnesses = map(toolbox.evaluate, invalid_ind)
for ind, fit in zip(invalid_ind, fitnesses):
ind.fitness.values = fit
print('Evaluated', len(invalid_ind), 'individuals’)
# The population is entirely replaced by the offspring
population[:] = offspring
Print the stats for the current generation to see how it's progressing:
# Gather all the fitnesses in one list and print the stats
fits = [ind.fitness.values[0] for ind in population]
length = len(population)
mean = sum(fits) / length
sum2 = sum(x*x for x in fits)
std = abs(sum2 / length - mean**2)**0.5
print('Min =', min(fits), ', Max =', max(fits))
print('Average =', round(mean, 2), ', Standard deviation =', round(std, 2))
print("n==== End of evolution")
best_ind = tools.selBest(population, 1)[0]
print('nBest individual:n', best_ind)
print('nNumber of ones:', sum(best_ind))

OUTPUT
As seen in the preceding figure, the evolution
process ends after 60 generations
(zeroindexed). Once it's done, the best
individual is picked and printed on the output.
It has 45 ones in the best individual, which is
like a confirmation for us because the target
sum is 45 in our evaluation function.

Applications of Genetic
Algorithm
• Recurrent Neural Network
• Mutation testing
• Code breaking
• Filtering and signal processing
• Learning fuzzy rule base etc.
• Traffic and Shipment Routing
(Travelling Salesman Problem)
• Robotics

Evolution
• Evolution is the change in the characteristics of a
species over several generations and relies on the
process of natural selection.
• It is a process of gradual change that takes place
over many generations, in a particular situation or
thing over a period of time.

Evolutionary Algorithm
• An evolutionary algorithm is a meta heuristic
optimization algorithm that applies the principles
of evolution to solve problems.
• The concept of evolution is similar to the one we
find in nature.
• The underlying idea in all evolutionary algorithms
is that we take a population of individuals and
apply the natural selection process.

Genetic Algorithm
• A genetic algorithm is an evolutionary algorithm where
we use a heuristic to find a string of bits that solves a
problem. We continuously iterate on a population to
arrive at a solution.
• We do this by generating new populations containing
stronger individuals
• In a genetic algorithm, any given problem is encoded in
bit patterns that are manipulated by the algorithm.
• We apply probabilistic operators such as selection,
crossover, and mutation in order to generate the next
generation of individuals.

Population
• A population is a set of individuals that are possible
candidate solutions.
• In a genetic algorithm, we do not maintain a single
best solution at any given stage. It maintains a set
of potential solutions, one of which is the best.

Operators
• Mutation:
• A genetic algorithm makes random changes to one or more
individuals of the current generation to yield a new
candidate solution
• This change is called mutation.
• Recombination/crossover:
• A genetic algorithm tries to combine individuals from the
current generation to create a new solution. It combines
some of the features of each parent individual to create this
offspring. This process is called crossover.
• The goal is to replace the weaker individuals in the current
generation with offspring generated from stronger
individuals in the population.

• In order to apply crossover and mutation, we need to
have selection criteria. The concept of selection is
inspired by the theory of natural selection.
• During each iteration, the genetic algorithm performs a
selection process.
• The selection process is carried out using a fitness
function that computes the strength of each individual.
• A fitness function is used that evaluates the fitness
measure of each string telling us how well suited it is to
solve the problem.
• This fitness function is also referred to as an evaluation
function.
Selection Criteria

• We start with a set of randomly selected individuals and
then identify the strongest among them. The strength of
each individual is determined using a fitness function that's
predefined. In a way, we use the survival of the fittest
approach.
• We then take these selected individuals and create the next
generation of individuals by recombination and mutation.
• Once we execute recombination and mutation, we create a
new set of individuals who will compete with the old ones
for a place in the next generation. By discarding the weakest
individuals and replacing them with offspring, we are
increasing the overall fitness level of the population. We
continue to iterate until the desired overall fitness is
achieved

Visualizing the evolution
• we can visualize the evolution process using Covariance
Matrix Adaptation Evolution Strategy (CMA-ES).
• It is an evolutionary algorithm that's used to solve non-
linear problems in the continuous domain. CMA-ES
technique is robust, well studied, and is considered as
state of the art in evolutionary algorithms.
• CMA-ES samples solutions from a multivariate gaussian
distribution. After evaluating all solutions, the solutions
are sorted by evaluation values, then updating the
distribution parameters (i.e., the mean vector and the
covariance matrix) based on the ranking of evaluation
values.

• The CMA-ES works through a cycle of stages:

CMA-ES in Evolution
1. Importing libraries
1. Define fitness / evaluation function
1. Define generate and update methods

4. Defining the number of individuals and the
number of generations
4. Create a HallOfFame object.
4. Evaluating the stats using the Statistics method

7. Iterate through the generations
7. Evaluate individuals using the fitness function
7. Update the hall of fame and statistics with the
current generation of individuals

10.Define the x axis and plot the stats

Convergence
• The evolution keeps running until some termination condition is
fulfilled. The best chromosome encountered so far is then
considered as the found solution.
• Convergence is a phenomenon in evolutionary computation that
causes evolution to halt because precisely every individual in the
population is identical.
• Premature convergence is caused by an early homogenization of
genetic material in the population. This means that no valuable
exploration can be performed anymore.
• However, convergence is not necessarily a negative
phenomenon, because populations often stabilize after a time, in
the sense that the best programs all have a common ancestor
and their behavior is very similar/identical both to each other and
to that of high fitness programs from the previous generations.

Understanding evolutionary
algorithms
• An evolutionary algorithm is a meta heuristic optimization algorithm that applies the principles of evolution
to solve problems. We directly use the problem's functions and variables to arrive at the solution.
• The underlying idea in all evolutionary algorithms is that we take a population of individuals and apply the
natural selection process. We start with a set of randomly selected individuals and then identify the strongest
among them. The strength of each individual is determined using a fitness function that's predefined. In a
way, we use the survival of the fittest approach.
• We then take these selected individuals and create the next generation of individuals by recombination and
mutation.
• Once we execute recombination and mutation, we create a new set of individuals who will compete with the
old ones for a place in the next generation. By discarding the weakest individuals and replacing them with
offspring, we are increasing the overall fitness level of the population. We continue to iterate until the
desired overall fitness is achieved.

• A genetic algorithm is an evolutionary algorithm where we use a heuristic to find a string
of bits that solves a problem. We continuously iterate on a population to arrive at a
solution. We do this by generating new populations containing stronger individuals.
• We apply probabilistic operators such as selection, crossover, and mutation in order to
generate the next generation of individuals.
• A fitness function is used that evaluates the fitness measure of each string telling us how
well suited it is to solve this problem. This fitness function is also referred to as
an evaluation function.
Understanding genetic algorithms

Fundamental concepts in genetic algorithms
• One of the most important aspects of genetic algorithms is the randomness. In order to iterate,
it relies on the random sampling of individuals. This means that the process is non-deterministic.
So, if you run the same algorithm multiple times, you might end up with different solutions.
• A population is a set of individuals that are possible candidate solutions. In a genetic algorithm,
we do not maintain a single best solution at any given stage. It maintains a set of potential
solutions, one of which is the best.

Solving the symbol regression problem
• It is important to understand that genetic programming is not the same as genetic algorithms.
Genetic programming is a type of evolutionary algorithm in which the solutions occur in the form of
computer programs. Basically, the individuals in each generation would be computer programs and
their fitness level corresponds to their ability to solve problems. These programs are modified, at
each iteration, using a genetic algorithm. In essence, genetic programming is the application of a
genetic algorithm.
• Coming to the symbol regression problem, we have a polynomial expression that needs to be
approximated here. It's a classic regression problem where we try to estimate the underlying
function. In this example, we will use the expression: f(x) = 2x^3 - 3x^2 + 4x - 1

import operator
import math
import random
import numpy as np
from deap import algorithms, base, creator, tools, gp
The code here is a variant of the symbol regression problem given in the DEEP library. Create a
new Python file and import the following:
Create a division operator that can handle divide-by-zero error gracefully:
# Define new functions
def division_operator(numerator, denominator):
if denominator == 0:
return 1
return numerator / denominator
Define the evaluation function that will be used for fitness calculation. We need to define a callable
function to run computations on the input individual:
# Define the evaluation function
def eval_func(individual, points):
# Transform the tree expression in a callable function
func = toolbox.compile(expr=individual)

Compute the mean squared error (MSE) between the function defined earlier and the original
expression:
# Evaluate the mean squared error
mse = ((func(x) - (2 * x**3 - 3 * x**2 - 4 * x + 1))**2 for x in points)
return math.fsum(mse) / len(points),
Define a function to create the toolbox. In order to create the toolbox here, we need to create a set of
primitives. These primitives are basically operators that will be used during the evolution. They serve as
building blocks for the individuals. We are going to use basic arithmetic functions as our primitives here:
# Function to create the toolbox
def create_toolbox():
pset = gp.PrimitiveSet("MAIN", 1)
pset.addPrimitive(operator.add, 2)
pset.addPrimitive(operator.sub, 2)
pset.addPrimitive(operator.mul, 2)
pset.addPrimitive(division_operator, 2)
pset.addPrimitive(operator.neg, 1)
pset.addPrimitive(math.cos, 1)
pset.addPrimitive(math.sin, 1)
We now need to declare an ephemeral constant. It is a special terminal type that does not have a fixed
value. When a given program appends such an ephemeral constant to the tree, the function gets
executed. The result is then inserted into the tree as a constant terminal. These constant terminals can
take the values -1, 0 or 1:
pset.addEphemeralConstant("rand101", lambda: random.randint(-1,1))

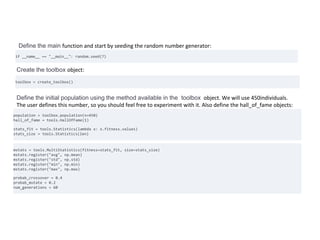
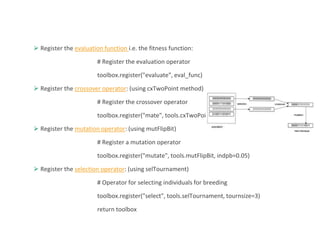
The default name for the arguments is ARGx. Let's rename it x. It's not exactly necessary, but it's a useful feature
that comes in handy:
pset.renameArguments(ARG0='x')
We need to define two object types - fitness and an individual. Let's do it using the creator:
creator.create("FitnessMin", base.Fitness, weights=(-1.0,)) creator.create("Individual", gp.PrimitiveTree,
fitness=creator.FitnessMin)
Create the toolbox and register the functions. The registration process is similar to previous sections:
toolbox = base.Toolbox()
toolbox.register("expr", gp.genHalfAndHalf, pset=pset, min_=1, max_=2)
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.expr)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
toolbox.register("compile", gp.compile, pset=pset)
toolbox.register("evaluate", eval_func, points=[x/10. for x in range(-10,10)])
toolbox.register("select", tools.selTournament, tournsize=3)
toolbox.register("mate", gp.cxOnePoint)
toolbox.register("expr_mut", gp.genFull, min_=0, max_=2)
toolbox.register("mutate", gp.mutUniform, expr=toolbox.expr_mut, pset=pset)
toolbox.decorate("mate", gp.staticLimit(key=operator.attrgetter("height"), max_value=17))
toolbox.decorate("mutate", gp.staticLimit(key=operator.attrgetter("height"), max_value=17))
return toolbox

Define the main function and start by seeding the random number generator:
if __name__ == "__main__": random.seed(7)
Create the toolbox object:
toolbox = create_toolbox()
Define the initial population using the method available in the toolbox object. We will use 450individuals.
The user defines this number, so you should feel free to experiment with it. Also define the hall_of_fame objects:
population = toolbox.population(n=450)
hall_of_fame = tools.HallOfFame(1)
stats_fit = tools.Statistics(lambda x: x.fitness.values)
stats_size = tools.Statistics(len)
Register the stats using the objects defined previously
mstats = tools.MultiStatistics(fitness=stats_fit, size=stats_size)
mstats.register("avg", np.mean)
mstats.register("std", np.std)
mstats.register("min", np.min)
mstats.register("max", np.max)
probab_crossover = 0.4
probab_mutate = 0.2
num_generations = 60

Run the evolutionary algorithm using the above parameters:
population, log = algorithms.eaSimple(population, toolbox,
probab_crossover, probab_mutate, num_generations,
stats=mstats, halloffame=hall_of_fame, verbose=True)
If you run the code, you will see the following on your Terminal at the start of the evolution:

At the end, you will see the following:

The goal of the intelligent robot controller is to automatically traverse
the map and consume all targets.
GOAL

DEAP
• It stand for Distributed Evolutionary Algorithms In Python
• DEAP is a novel evolutionary computation framework for
rapid prototyping and testing of ideas.
• It seeks to make algorithms explicit and data structures
transparent. It works in perfect harmony with
parallelization mechanisms such as multiprocessing and
SCOOP.
• DEAP is compatible with Python 2.7 and 3.4 or higher.
• Command to install : pip install deap
LIBRARY USED

Introduction
● One of the capabilities of robots is to move from one point to another which called is
autonomous navigation.
● Autonomous robot is a robot that can perform certain work independently without the
human help.
● There are many techniques that can be used to solve the problem of building Intelligent
Robot controller. Some of them include genetic algorithm (GA)
● To apply an algorithm to the robotic as a method of designing robotic controllers that
enable the robot to perform complex tasks and behaviors.
Robot Controller

Introduction
● Genetic Algorithm is a search-based optimization technique based on the principles
of Genetics and Natural Selection.
● It is frequently used to find optimal or near-optimal solutions to difficult problems
which otherwise would take a lifetime to solve.
● It is frequently used to solve optimization problems, in research, and in machine
learning.
● It uses techniques inspired by biological evolution such as inheritance, mutation,
selection, and crossover.
Genetic algorithm

• Initialize Population : genetic algorithms begin by initializing a Population of
candidate solutions. A candidate solution is a Chromosome that is
characterized by a set of parameters known as Genes.
• Evaluate : next, the population is evaluated by assigning a fitness value to each
individual in the population.
After evaluation, the algorithm decides whether it should terminate the search depending on the termination conditions set.
When the termination condition is finally met, the algorithm will break out of the loop and typically return its finial search results back to the user.
Working of GA

• Selection : if the termination condition is not met, the population goes through a selection
stage in which individuals from the population are selected based on their fitness score.
• Crossover : the next stage is to apply crossover and mutation to the selected individuals.
• Mutation : at this point the new population goes back to the evaluation step and the process
starts again.
• Each cycle of this loop is called as generation.
WORKING OF GA

The Robot has to follow the given path
using Generic Algorithm.
The symbol ‘#’ indicates all the targets on
the map and the symbol ‘S’ indicates the
starting point. The symbol ‘.’ denotes empty
cells
Robot can take four actions
• Move one step forward
• Turn left
• Turn right
• Do nothing

1. Define the main function and start by seeding the
random number generator
2. Create object of robot class having parameterized
constructor who initializes program.
3. Create toolbox using DEAP python library
• Add and set primitives in toolbox function such as turn left, turn right, move forward
4. Now read the map given in the file,
where The symbol ‘#’ indicates all the targets on
the map and the symbol ‘S’ indicates the starting point.
The symbol ‘.’ denotes empty cells
Algorithm

5. Define the population followed by registering the
stats
6. Define the crossover probability, mutation
probability, and the number of generations
7. Run the evolutionary algorithm using earlier
defined parameters
Algorithm

Introduction to Artificial Intelligence...pptx

More Related Content

Similar to Introduction to Artificial Intelligence...pptx

Recently uploaded

Introduction to Artificial Intelligence...pptx