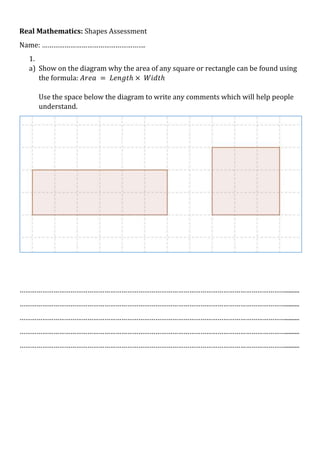
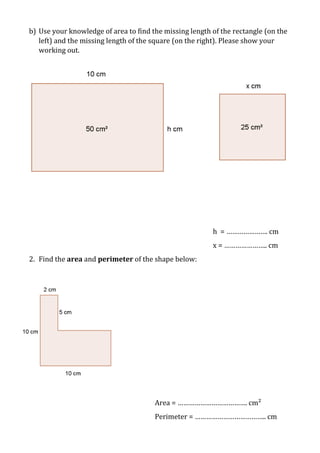
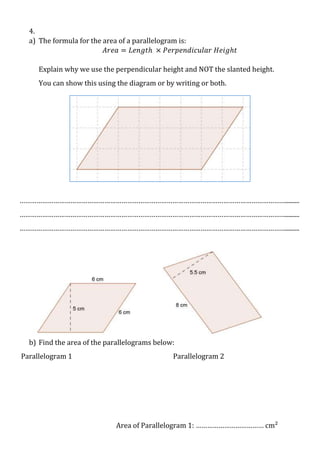
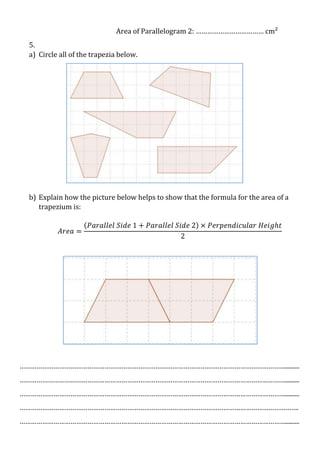
This document is a mathematics assessment on shapes that tests a student's knowledge of area formulas for squares, rectangles, triangles, parallelograms, trapezoids, and hexagons. It contains questions that require the student to find missing lengths, calculate areas and perimeters, explain area formulas visually or in writing, and apply the formulas to find the areas of various shapes. The assessment provides space for work and explanations to demonstrate understanding of geometric concepts and area calculations.

1. Real Mathematics: Shapes Assessment
Name: ……………………………………………….
1.
a) Show on the diagram why the area of any square or rectangle can be found using
the formula:
Use the space below the diagram to write any comments which will help people
understand.
…………………………………………………………………………………………………………………………….........
…………………………………………………………………………………………………………………………….........
…………………………………………………………………………………………………………………………….........
…………………………………………………………………………………………………………………………….........
…………………………………………………………………………………………………………………………….........

2. b) Use your knowledge of area to find the missing length of the rectangle (on the
left) and the missing length of the square (on the right). Please show your
working out.
h = …………………. cm
x = ………………….. cm
2. Find the area and perimeter of the shape below:
Area = ………………………………. cm²
Perimeter = ……………………………….. cm

3. 3.
a) Can you explain, using a diagram or writing or both, why the area of any triangle
can be found using the formula:
…………………………………………………………………………………………………………………………….........
…………………………………………………………………………………………………………………………….........
…………………………………………………………………………………………………………………………….........
…………………………………………………………………………………………………………………………….........
b) Use the space below to make two different triangles which have an area of
12 cm². You DO NOT have to draw these shapes with a ruler.

4. 4.
a) The formula for the area of a parallelogram is:
Explain why we use the perpendicular height and NOT the slanted height.
You can show this using the diagram or by writing or both.
…………………………………………………………………………………………………………………………….........
…………………………………………………………………………………………………………………………….........
…………………………………………………………………………………………………………………………….........
b) Find the area of the parallelograms below:
Parallelogram 1
Parallelogram 2
Area of Parallelogram 1: ……………………………… cm²

5. Area of Parallelogram 2: ……………………………… cm²
5.
a) Circle all of the trapezia below.
b) Explain how the picture below helps to show that the formula for the area of a
trapezium is:
…………………………………………………………………………………………………………………………….........
…………………………………………………………………………………………………………………………….........
…………………………………………………………………………………………………………………………….........
………………………………………………………………………………………………………………………………….
…………………………………………………………………………………………………………………………….........

6. ………………………………………………………………………………………………………………………………….
6.
a) Show three different ways that you could split up the hexagon to find its area.
b) By measuring any necessary parts of the hexagon, find itsarea in millimetres
squared (mm²).

7. Area of Hexagon = ………………………………mm²