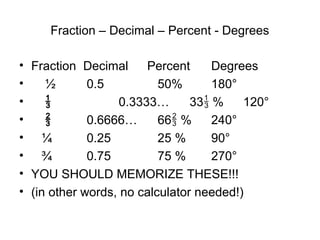
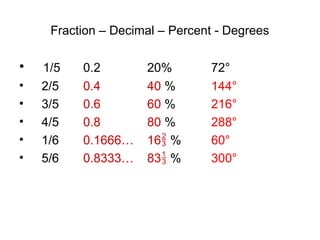
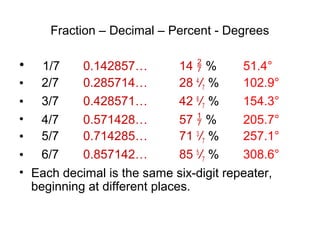
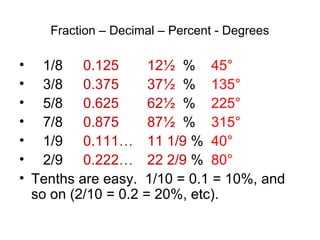
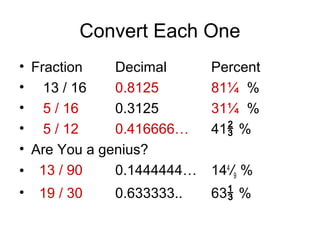
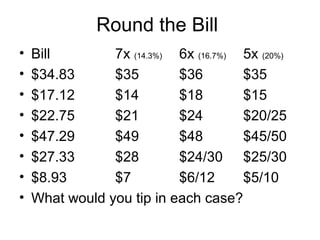
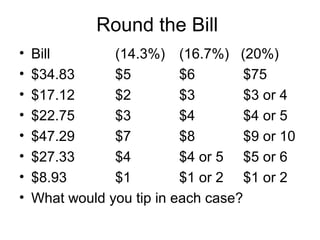
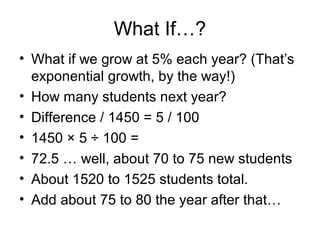The document provides information on converting between fractions, decimals, percents, and degrees. It includes examples for common fractions like 1/2, 1/4, and 3/4. It then works through converting other fractions like 1/7, 1/8, and 1/9. The document demonstrates patterns that emerge and discusses estimating fractions from percents. It also covers applications like calculating tips and sales. The overall purpose is to help the reader develop fluency in interconverting between fractional representations.

1. KNOW YOUR NUMBERS!
Factors, Multiples, Fractions,
Percents, Estimates, Change
From a Dollar, Tips

2. FRACTIONS, DECIMALS,
PERCENTS, & ANGLES
Convert from one to any of
the other three… with or
without a calculator!

3. Purpose
• Know your numbers! In this case,
understand how to convert fractions to
decimals, percents, or pieces of a circle.
• Get a “feel” for each. Estimate a fraction
based on the decimal. Create a circle
graph given a percent or a fraction.
• Circle has 360 degrees. Multiply fraction,
decimal, or percent times 360.

4. Fraction – Decimal – Percent - Degrees
• Fraction Decimal Percent Degrees
• ½ 0.5 50% 180°
•  0.3333… 33 % 120°
•  0.6666… 66 % 240°
• ¼ 0.25 25 % 90°
• ¾ 0.75 75 % 270°
• YOU SHOULD MEMORIZE THESE!!!
• (in other words, no calculator needed!)

5. Fraction – Decimal – Percent - Degrees
• 1/5 0.2 20% 72°
• 2/5 ____ ____ % ___°
• 3/5 ____ ____ % ___°
• 4/5 ____ ____ % ___°
• 1/6 ____ ____ % ___°
• 5/6 ____ ____ % ___°
• Why didn’t I include 2/6, 3/6, and 4/6?
• Simplified: 1/3, ½, and 2/3. You have ‘em!

6. Fraction – Decimal – Percent - Degrees
• 1/5 0.2 20% 72°
• 2/5 0.4 40 % 144°
• 3/5 0.6 60 % 216°
• 4/5 0.8 80 % 288°
• 1/6 0.1666… 16 % 60°
• 5/6 0.8333… 83 % 300°

7. Fraction – Decimal – Percent - Degrees
7 is not a factor of 360, so round the percents and degrees
to 1 decimal place. Write decimal to six places, however.
• 1/7 ______ _____ % ____°
• 2/7 ______ _____ % ____°
• 3/7 ______ _____ % ____°
• 4/7 ______ _____ % ____°
• 5/7 ______ _____ % ____°
• 6/7 ______ _____ % ____°
• What patterns do you notice?

8. Fraction – Decimal – Percent - Degrees
• 1/7 0.142857… 14  % 51.4°
• 2/7 0.285714… 28 4/7 % 102.9°
• 3/7 0.428571… 42 6/7 % 154.3°
• 4/7 0.571428… 57  % 205.7°
• 5/7 0.714285… 71 3/7 % 257.1°
• 6/7 0.857142… 85 5/7 % 308.6°
• Each decimal is the same six-digit repeater,
beginning at different places.

9. Fraction – Decimal – Percent - Degrees
• 1/8 _____ _____ % ____°
• 3/8 _____ _____ % ____°
• 5/8 _____ _____ % ____°
• 7/8 _____ _____ % ____°
• Again, what patterns do you notice?
• Do the ninths (1/9, 2/9, etc.) and find the easy
pattern for them.

10. Fraction – Decimal – Percent - Degrees
• 1/8 0.125 12½ % 45°
• 3/8 0.375 37½ % 135°
• 5/8 0.625 62½ % 225°
• 7/8 0.875 87½ % 315°
• 1/9 0.111… 11 1/9 % 40°
• 2/9 0.222… 22 2/9 % 80°
• Tenths are easy. 1/10 = 0.1 = 10%, and
so on (2/10 = 0.2 = 20%, etc).

11. F–D–P–D
• 1/11 0.090909… 9 1/11 % 32.7°
• 2/11 0.181818… 18 2/11 % 65.5°
• 3/11 0.272727… 27 3/11 % 98.2°
• You should be able to see the pattern for
the remaining elevenths.
• Now you do the twelfths.
• You should be able to convert any fraction
to a decimal or percent.

12. Converting Back & Forth
• To convert any fraction or decimal to a
percent, multiply by 100.
• To convert any percent to a fraction or
decimal, divide by 100.
• abcDefghijklmnoPqrstuvwxyz
• Decimal to Percent .  2 places
• Percent to Decimal  . 2 places

13. Convert Each One
• Fraction Decimal Percent
• 13 / 16 ______ _____ %
• _____ 0.3125 _____ %
• _____ _____ 41 %
• Try these to show you’re a genius:
• _____ 0.1444444… 144/9 %
• _____ 0.633333.. 63 %

14. Convert Each One
• Fraction Decimal Percent
• 13 / 16 0.8125 81¼ %
• 5 / 16 0.3125 31¼ %
• 5 / 12 0.416666… 41 %
• Are You a genius?
• 13 / 90 0.1444444… 144/9 %
• 19 / 30 0.633333.. 63 %

15. Estimate the Fraction
• Suppose you have a percent, and need to
“think” of it as a relatively simple fraction,
involving halves, thirds, fourths, fifths, etc.
• Round the percent to one that matches a
fraction that you know.
• Example: 43.7% is a tad more than 40%,
which is 2/5. So, if 43.7% voted for
Candidate X, then about 2 out of every 5
voters voted for him.

16. Estimate the Fraction
• 35% is a bit more than ….
• One third
• 72% is just a hair less than…
• Three fourths
• 83% is almost exactly…
• Five sixths
• 60% is exactly…
• Three fifths

17. Estimate the Fraction
• 38.7%
• About 2/5th
• 13%
• About 1/8th
• 14.5%
• About 1/7th
• 17%
• About 1/6th

18. Tip?
• Granted, most of you don’t even think
about tipping the server (waiter/waitress),
but most adults do!
• “Standard” tip is about 15 to 18%.
• Think about these fractions & percents:
• 1/7 = 14.3% 1/6 = 16.7% 1/5 = 20%
• What would you tip for average, good, or
super service on a $21.97 bill?

19. Tip on $21.97?
• If you tip $1 for every $7 you spend, that’s
a bit more than 14%. For every $6 you
spend, that’s almost 17%. For every $5
you spend, that’s 20%.
• A $3 tip (3 × 7 = 21) is less than 15%, but
a $4 tip is about 18%.
• Round the bill to the nearest multiple of 7,
6, or 5, based on your tipping percentage.

20. Round the Bill
• Bill 7x (14.3%) 6x (16.7%) 5x (20%)
• $34.83 $35 $36 $35
• $17.12 $14 $18 $15
• $22.75 ____ ____ ____
• $47.29 ____ ____ ____
• $27.33 ____ ____ ____
• $8.93 ____ ____ ____
• What would you tip in each case?

21. Round the Bill
• Bill 7x (14.3%) 6x (16.7%) 5x (20%)
• $34.83 $35 $36 $35
• $17.12 $14 $18 $15
• $22.75 $21 $24 $20/25
• $47.29 $49 $48 $45/50
• $27.33 $28 $24/30 $25/30
• $8.93 $7 $6/12 $5/10
• What would you tip in each case?

22. Round the Bill
• Bill (14.3%) (16.7%) (20%)
• $34.83 $5 $6 $75
• $17.12 $2 $3 $3 or 4
• $22.75 $3 $4 $4 or 5
• $47.29 $7 $8 $9 or 10
• $27.33 $4 $4 or 5 $5 or 6
• $8.93 $1 $1 or 2 $1 or 2
• What would you tip in each case?

23. Tip: Cash or Plastic?
• If you’re leaving cash on the table, you
probably leave whole dollars, or maybe
dollars and a couple of quarters.
• But, if you’re using plastic, what’s typical?
• Suppose bill is $23.71. If you’re tipping a
dollar for every $6 you spend, that’s about
$4. So, tip is $4.29, which brings total bill
to $28.00

24. Change From A Dollar
• If you’re paying in cash, don’t you want
correct change? Of course! What’s the
change back from a dollar :
• $.53 $.82 $.67 $.39
• $.47 $.18 $.33 $.61
• Can you do this quickly, in your head?
• $.34 $.29 $.58 $.74
• $.66 $.71 $.42 $.26

25. PERCENTS
Solve Percent Problems

26. Percent Proportion
• Use this proportion to solve percent
problems.
• IS Percent
• =
• OF 100

27. Solving Percent Problems
• Use the “IS over OF equals Percent Over
One Hundred” proportion.
• When the problem calls for a percent of
increase (growth) or decrease (decline),
use “Difference” as the “IS” and “OLD” as
the “OF.”
• Difference = New – Old.

28. Solve
• What is 33 1/3 % of 123?
• Hint: 33 1/3% is one-third! Just divide by
3, or, set up proportion: is/of = 1/3
• 41
• 18 correct on a 22 question quiz is what
percent correct?
• 819/11 % (81.8, rounded to nearest tenth)

29. Solve
• 13,500 voters represent 25% of the
eligible voting population. How many
people are eligible to vote?
• 13,500 = “IS” 25% out of 100 is ¼ , so
you could just multiply by 4.
• 13,500 / x = 25 / 100  13,500 / x = 1 / 4
• Total population (the “OF”) = 54,000.

30. Percent of Change
• Last year, we had about 1380 students.
This year, it’s about 1450. What percent
of change is that?
• Step 1: Find the difference. 1450 – 1380
is an increase of 70 students.
• Step 2: Use “Diff / Old = % / 100”
proportion, cross-multiplying & dividing.
• 100 × 70 ÷ 1380 ≈ 5.1% increase

31. What If…?
• What if we grow at 5% each year? (That’s
exponential growth, by the way!)
• How many students next year?
• Difference / 1450 = 5 / 100
• 1450 × 5 ÷ 100 =
• 72.5 … well, about 70 to 75 new students
• About 1520 to 1525 students total.
• Add about 75 to 80 the year after that…

32. “B O G O”
• Many stores have “BOGO” sales. “Buy
One, Get One” or sometimes “Buy Two,
Get One,” and so on. What percent do
you save?
• Example: “Buy one, get one free” is a
50% savings, since 1 free out of 2 is ½.
• Ex: “Buy two, get one free” is a 33 1/3%
savings. (1 out of 3 is free)

33. BOGO
• Suppose you see: “Buy one, get second
half off.” What percent is savings?
• Think: If you had to pay full price for two,
that’s the equivalent of 200%. You pay
100% for the first one, but 50% for the
second. So you pay 150% vs. 200%.
• 200 – 150 = 50. You save 50 out of 200
• 50 / 200 = 0.25 You save 25%

34. Which is Cheaper?
• Macy’s is having a sale, where everything
in the store is 15% off. Their regular price
of a pair of shoes is $44.95.
• Dillards is having a sale on those same
shoes, which are discounted 20%. Their
regular price is $48.95.
• J C Penney’s sells the same shoes at
$38.95.
• Which store has the cheaper shoes?

35. Cheaper Shoes?
• Macy’s: 15% × $44.95 = $6.74 Subtract
to get price of $38.21. Dillards: 20% ×
48.95 = $9.79 Subtract to get price of
$39.16 Dillards is more expensive
• All prices within a dollar and change of
each other, Macy’s slightly cheaper.
• Alternate method: 100% – 15% = 85%
Multiply $44.95 × 85% = $38.21