sdf

1. UNIVERSIDAD NACIONAL DE CHIMBORAZO
FACULTAD DE CIENCIAS POLÍTICAS Y ADMINISTRATIVAS
CARRERA DE CONTABILIDAD Y AUDITORÍA CPA
Nombre: RAUL LOGROÑO
Curso: 5to Semestre
Paralelo: “A”
Fecha: 27 de Mayo del 2015
Tema: Matriz aumentada
EJERCICIO 01
1
2
3
-1 2
2 -4 -1 4
4 2 -5 7
3 2 -3 6 f1 ÷3
2 -4 -1 4
4 2 -5 7
1
2
3
-1 2
0 −
16
3
1 0 -2f1+f2
0 −
2
3
-1 -1 -4f1+f3
{
3𝑋1 + 2𝑌 − 3𝑍 = 6
3𝑋 − 4𝑌 − 𝑍 = 4
4𝑋 + 2𝑌 − 5𝑍 = 7
-2 −
4
3
2 -4
2 -4 -1 4
-4 −
8
3
-4 -8
4 2 -5 7

2. X=
25
9
Y=
1
6
Z=
8
9
1
2
3
-1 2
0 1 −
3
16
0 f1÷−
16
3
0 −
2
3
-1 -1
1 0 −
7
8
2 −
2
3
×f2+f1
0 1 −
3
16
0
0 0 −
9
8
-1
2
3
×f2+f3
1 0 −
7
8
2
0 1 −
3
16
0
0 0 1
8
9
f3×−
8
9
1 0 0
25
9
7
8
f3+f1
0 1 0
1
6
3
16
f3+f2
0 0 1
8
9
0 −
2
3
1
8
0
1 2
3
-1 2
0 2
3
−
1
8
0
0 −
2
3
-1 -1
0 0 7
8
7
9
1 0 −
7
8
2
0 0 3
16
1
6
0 1 −
3
16
0

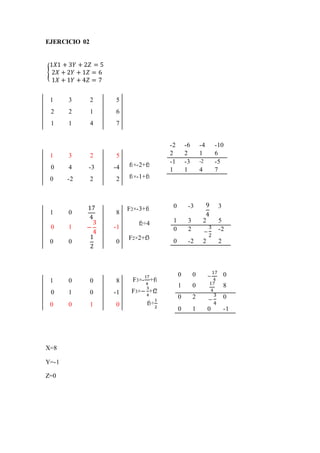
3. EJERCICIO 02
X=8
Y=-1
Z=0
1 3 2 5
2 2 1 6
1 1 4 7
1 3 2 5
0 4 -3 -4 f1×-2+f2
0 -2 2 2 f1×-1+f3
1 0
17
4
8
F2×-3+f1
0 1 −
3
4
-1
f2÷4
0 0
1
2
0
F2×2+f3
1 0 0 8 F3×-
17
4
+f1
0 1 0 -1 F3×−
3
4
+f2
0 0 1 0 f3÷
1
2
{
1𝑋1 + 3𝑌 + 2𝑍 = 5
2𝑋 + 2𝑌 + 1𝑍 = 6
1𝑋 + 1𝑌 + 4𝑍 = 7
-2 -6 -4 -10
2 2 1 6
-1 -3 -2 -5
1 1 4 7
0 -3 9
4
3
1 3 2 5
0 2 −
3
2
-2
0 -2 2 2
0 0 −
17
4
0
1 0 17
4
8
0 2 −
3
4
0
0 1 0 -1

4. EJERCICIO 03
X=-16
Y=-18
Z=3
1 -1 2 2
3 -4 1 3
2 -2 3 1
1 -1 2 2
0 -1 -5 -3 F1×-3+f2
0 0 -1 -3 F1×-2+f3
1 0 7 5 F2×1+f1
0 1 5 3 F2÷-1
0 0 -1 -3
1 0 0 -16 F3×-7+f1
0 1 0 18 F3×-5+f2
0 0 1 3 f3÷-1
{
1𝑋 − 1𝑌 + 2𝑍 = 2
3𝑋 − 4𝑌 + 1𝑍 = 3
2𝑋 − 2𝑌 + 3𝑍 = 1
-3 3 -6 -6
3 -4 1 3
-2 2 -4 -4
2 -2 3 1
0 1 5 3
1 -1 2 2
0 0 -7 -21
1 0 7 5
0 0 -5 -15
0 1 5 -3

5. EJERCICIO 0
X=
489
112
Y=
31
56
Z=
45
112
1
3
2
2 6
f1÷2
0
13
2
-1 -4
f1×-3+f2
0 -9 -10 9 f1×-4+f3
1 0
23
13
66
13
f2×−
3
2
+f1
0 1
2
13
8
13
f2×−
2
13
0 0
112
12
−
45
13
f2×9+f3
1 0 0
489
112
f3×−
23
13
+f1
0 1 0
31
56
f3×-−
2
13
+f2
0 0 1
45
112
f3×
12
112
{
2𝑋 + 3𝑌 + 4𝑍 = 12
3𝑋 − 2𝑌 + 5𝑍 = 14
4𝑋 − 3𝑌 − 2𝑍 = 15