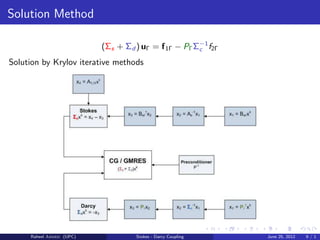
The document presents a master's thesis on the numerical approximation of filtration processes through porous media, focusing on the Stokes-Darcy coupling. It discusses objectives such as mixed finite element discretization, Schur complement methods for solving coupled problems, and various preconditioners for iterative solving techniques. The work includes extensive numerical tests and formulation details for both steady and unsteady problems in filtration applications.

1. Numerical Approximation of Filtration Processes through
Porous Medium
Master Thesis Presentation
Raheel Ahmed
Supervisor: Marco Discacciati
Universitat Polit`ecnica de Catalunya - Barcelona Tech
CIMNE
June 25, 2012
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 1 / 1

2. Introduction
Free fluid flow coupled with porous medium flow.
Importance in industrial and natural processes
Membrane filtration processes
Air or oil filters
Blood flow through body tissues
Forward osmosis processes
Numerical analysis of the coupled problem
[Campbell, Biology 2009]
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 2 / 1

3. Objectives
Mixed finite element discretization for both fluid regions.
Investigation of the optimum solution method based on preconditioning the
Schur complement system.
“...at this very moment the search is on - every numerical analyst has a favorite
preconditioner, and you have a perfect chance to find a better one.”
-Gil Strang (1986)
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 3 / 1

4. Problem Statement
nd Γ
Ωs
Ωd
∂Ωs,N
∂Ωs,N
∂Ωd,D
∂Ωd,N
∂Ωs,D
∂Ωd,N
n
n
Stokes Equation
−ν△us + ∇ps = f in Ωs
∇ · us = 0 in Ωs
Darcy Equation
ud = −K∇pd in Ωd
∇ · ud = 0 in Ωd
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 4 / 1

5. Problem Statement
Interface Conditions
nd Γ
Ωs
Ωd
∂Ωs,N
∂Ωs,N
∂Ωd,D
∂Ωd,N
∂Ωs,D
∂Ωd,N
n
n
Conservation of mass across the interface:
us · n = ud · n, on Γ
Balance of normal forces across the interface:
−νn ·
∂us
∂n
+ ps = gpd on Γ
Beavers-Joseph-Saffman condition:
−ντj ·
∂us
∂n
=
ν
ǫ
us · τj (j = 1, 2 for 2D) on Γ
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 5 / 1

6. Steady Stokes Darcy Problem
Weak Formulation
Stokes Equations:
Ωs
ν∇u0
s · ∇vs −
Ωs
ps ∇ · vs +
Γ
gp0
d (vs · n) +
Γ
n−1
j=1
ν
ǫ
(u0
s · τj )(vs · τj ) =
Ωs
f · vs
−
Ωs
∇ · u0
s qs = 0
Darcy Equations:
Primal-mixed formulation
Addition of stability terms proposed by [Masud. 2002].
1
2
K−1
g
Ωd
ud · vd +
1
2
g
Ωd
∇p0
d · vd = 0
1
2 Ωd
gud · ∇qd +
Γ
g(u0
s · n)qd −
1
2 Ωd
g(K∇p0
d · ∇qd ) = 0
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 6 / 1

7. Steady Stokes Darcy Problem
Algebraic Formulation
By the finite element discretization, we get algebraic system as follows.
Stokes
P1 − P1 P2 − P2
Darcy








A1,ii A1,iΓ B1i 0 0 0
A1,Γi A1,ΓΓ B1Γ 0 0 PΓ
BT
1i BT
1Γ 0 0 0 0
0 0 0 A2 B2i B2Γ
0 0 0 BT
2i Sii SiΓ
0 PT
Γ 0 BT
2Γ SΓi SΓΓ















˜ui
s
uΓ
˜ps
˜ud
˜pi
d
pΓ







=







F1i
F1Γ
F12
F21
F2i
F2Γ







Large
Ill-Conditioned
Symmetric
Indefinite
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 7 / 1

8. Steady Stokes Darcy Problem
Algebraic Formulation








A1,ii A1,iΓ B1i 0 0 0
A1,Γi A1,ΓΓ B1Γ 0 0 PΓ
BT
1i BT
1Γ 0 0 0 0
0 0 0 A2 B2i B2Γ
0 0 0 BT
2i Sii SiΓ
0 PT
Γ 0 BT
2Γ SΓi SΓΓ















˜ui
s
uΓ
˜ps
˜ud
˜pi
d
pΓ







=







F1i
F1Γ
F12
F21
F2i
F2Γ











As BsΓ 0 0
BT
sΓ A1,ΓΓ 0 PΓ
0 0 Ad BdΓ
0 PT
Γ BT
dΓ SΓΓ








us
uΓ
ud
pΓ



 =




Fs
F1Γ
Fd
F2Γ




Schur complement system:
(Σs + Σd ) uΓ = f1Γ − PΓΣ−1
c f2Γ
(Σc + Σf ) pΓ = f2Γ − PT
Γ Σ−1
s f1Γ
Properties of Schur Complement
Smaller than original system
Better conditioned than the original system (O(h−1)).
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 8 / 1

9. Solution Method
(Σs + Σd ) uΓ = f1Γ − PΓΣ−1
c f2Γ
Solution by Krylov iterative methods
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 9 / 1

10. Numerical Tests
(Σs + Σd ) uΓ = f1Γ − PΓΣ−1
c f2Γ
(0, 1) × (0, 2)
Γ
∂Ωs,D
∂Ωd,N∂Ωd,N
∂Ωd,D
Ωs
∂Ωs,D
Ωd
∂Ωs,N
Structured mesh;
Elements: MINI &
P1 − P1
Residual tolerance for
solution = 1.e − 9
Conjugate Gradient without preconditioner
Number of iterations
Grid ν = 10−4
, ν = 10−6
, ν = 10−6
, ν = 100
,
K = 10−3
K = 10−5
K = 10−8
K = 100
1 4 4 4 4
2 9 9 10 8
3 20 20 24 16
4 33 34 39 28
Iterations increase with decrease in mesh size.
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 10 / 1

11. Iteration tests with Preconditioner
Dirichlet-Neumann Preconditioner
P−1
= Σ−1
s
Grid ν = 10−4
, ν = 10−6
, ν = 10−6
, ν = 100
,
K = 10−3
K = 10−5
K = 10−8
K = 100
1 4 4 4 4
2 10 10 10 5
3 24 24 30 5
4 50 53 64 5
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 11 / 1

12. Iteration tests with Preconditioner
GHSS Preconditioner (work by [Benzi, 2009])
P−1
= 2α(Σd + αI)−1
(Σs + αI)−1
Number of iterations
Grid ν = 10−4
, K = 10−3
ν = 10−6
, K = 10−5
ν = 10−6
, K = 10−8
ν = 100
, K = 100
1 4 (α = 1.e − 2) 2 (α = 1.e − 1) 1 (α = 1.e − 1) 4 (α = 1.e − 2)
2 5 (α = 1.e − 2) 2 (α = 1.e − 1) 1 (α = 1.e − 1) 8 (α = 1.e − 2)
3 5 (α = 1.e − 2) 2 (α = 1.e − 1) 1 (α = 1.e − 1) 11 (α = 1.e − 2)
4 7 (α = 1.e − 2) 3 (α = 1.e − 1) 1 (α = 1.e − 1) 10 (α = 1.e − 2)
−8 −7 −6 −5 −4 −3 −2
−4
−3
−2
−1
0
1
2
ν = 10
−4
log
10
K
log
10
α
y = − 0.05*x
3
− 0.74*x
2
− 4*x − 8.4
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 12 / 1

13. Iteration tests with Preconditioner
GHSS-Variant (1)
P−1
= 2αd (Σd + αd I)−1
(Σs + αsI)−1
Optimum results for αs > αd when ν, K < 1
GHSS-Variant (2)
P−1
= 2αd (Σd + αd I)−1
→ αd = 1.e − 3
Grid ν = 10−4, ν = 10−6, ν = 10−6,
K = 10−3 K = 10−5 K = 10−8
1 2 2 1
2 3 2 1
3 3 2 1
4 3 2 1
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 13 / 1

14. Iteration tests with Preconditioner
Neumann-Neumann Preconditioner
P−1
= θs
2
(Σs)−1
+ θd
2
(Σd )−1
where, θs = νK
νK+h and θd = h
νK+h with h being the mesh size.
Grid ν = 10−4
, ν = 10−6
, ν = 10−6
,
K = 10−3
K = 10−5
K = 10−8
1 2 1 1
2 2 1 1
3 2 1 2
4 3 1 1
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 14 / 1

15. Unsteady Stokes-Darcy Problem
∂us
∂t
− ν△us + ∇ps = f in Ωs
∇ · us = 0 in Ωs
ud = −K∇pd in Ωd
So
∂pd
∂t
+ ∇ · ud = 0 in Ωd
us · n = ud · n, on Γ
−νn ·
∂us
∂n
+ ps = gpd on Γ
−ντj ·
∂us
∂n
=
ν
ǫ
us · τj (j = 1, . . . , n − 1) on Γ.
nd Γ
Ωs
Ωd
∂Ωs,N
∂Ωs,N
∂Ωd,D
∂Ωd,N
∂Ωs,D
∂Ωd,N
n
n
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 15 / 1

16. Unsteady Stokes-Darcy Problem
Weak Formulation
Mixed finite element discretization
Time discretisation: Backward Euler Difference Scheme
Interface Systems
(Σs + Σd ) um+1
Γ = f1Γ − PΓΣ−1
c f2Γ
(Σc + Σf ) pm+1
Γ = f2Γ − PT
Γ Σ−1
s f1Γ
for every time tm, m = 0, . . . , N where N is number of time intervals
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 16 / 1

17. Unsteady Stokes-Darcy Problem
Preconditioners
Preconditioner Properties
Dirichlet Neumann CG solver
Σ−1
s K, ν ≥ 1
GHSS GMRES solver
2α(Σd + αI)−1
(Σs + αI)−1
α is not fixed
Multiplicative
GHSS variant(1) → GHSS variant (2) CG solver
2αd (Σd + αd I)−1
K, ν ≤ 1
Neumann-Neumann CG solver
θs
2
(Σs )−1
+ θd
2
(Σd )−1
K, ν ≤ 1
θs , θd can be controlled.
For Unsteady, identical behaviour as presented for Steady problem.
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 17 / 1

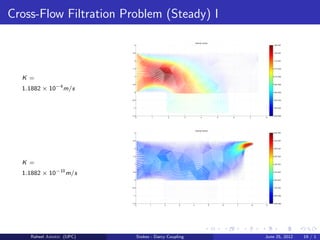
18. Cross-Flow Filtration Problem
[novasep]
ν = 0.08247m2/s
by [Hanspal et al., 2009]
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 18 / 1

19. Cross-Flow Filtration Problem (Steady) I
K =
1.1882 × 10−4
m/s
K =
1.1882 × 10−10
m/s
0 1 2 3 4 5 6 7 8
−1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
3
Velocity vectors
0.0E+000
1.6E−002
3.2E−002
4.9E−002
6.5E−002
8.1E−002
9.7E−002
1.1E−001
1.3E−001
1.5E−001
0 1 2 3 4 5 6 7 8 9
−1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
3
Velocity Vectors
0.0E+000
6.6E−002
1.3E−001
2.0E−001
2.7E−001
3.3E−001
4.0E−001
4.6E−001
5.3E−001
6.0E−001
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 19 / 1

20. Cross-Flow Filtration Problem (Steady) II
Number of elements Number of iterations for solution
Stokes Darcy Non-Preconditioned system Neumann-Neumann Preconditioned system
K = 1.1882 × 10−4
432 104 10 5
1728 416 17 5
6912 1664 25 5
K = 1.1882 × 10−10
432 104 10 3
1728 416 25 3
6912 1664 43 3
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 20 / 1

21. Cross-Flow Filtration Problem (Unsteady) I
Variation of Hyd. Conductivity near interface, with time.
Time Hyd. Conductivity Number of iterations
t(s) K(m/s) Non-Preconditioned Neumann-Neumann Preconditioner
1 1.1883 17 2
10 0.11883 17 2
20 0.00297 17 3
30 4.4009e-5 16 5
40 4.641e-7 12 12
50 3.802e-9 22 8
Simulation
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 21 / 1

22. Unsteady Stokes-Darcy Problem
Decoupled Method
Work by [Shan et al. 2011] extended to mixed discretisation in porous region.
Different time steps for different sub-domains
Stokes Darcy
∆s = n∆t
SΓ
∆t
Less number of time intervals for Darcy
Accuracy is compromised in Darcy domain.
Require refined mesh and small time intervals for better accuracy.
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 22 / 1

23. Conclusion
Optimum solution methods have been presented for coupled problem.
Can be employed for the numerical analysis of large practical problems.
Can be implemented into already available solvers.
Thank You!
Raheel Ahmed (UPC) Stokes - Darcy Coupling June 25, 2012 23 / 1