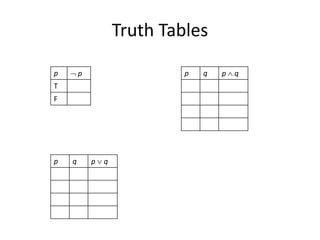
Discrete mathematics is the study of mathematical structures that are discrete rather than continuous. It considers objects that vary in a discrete way, such as digital watches showing integers of time, rather than analog watches with continuous hands. Problems in discrete mathematics cover non-continuous domains and consider questions about connecting cities with telephone lines or visiting islands with bridges without crossing any bridge twice. Logic and propositions are also key aspects of discrete mathematics, including defining statements, propositional variables, compound propositions using operators, truth tables, and negation, conjunction, disjunction and other operations.

1. Discrete Mathematics
MCA-105

2. Introduction
• Discrete mathematics is the study of
mathematical structures that are
fundamentally discrete rather than
continuous.

3. Discrete vs. Continuous Mathematics
Continuous Mathematics
It considers objects that vary continuously;
Example:
– Analog wristwatch (separate hour, minute, and second hands).
– 1:25 pm to 1:27pm
– Real-number system --- core of continuous mathematics;
Discrete Mathematics
It considers objects that vary in a discrete way.
Example:
– Digital wristwatch.
– Integers --- core of discrete mathematics

4. Problems Covered
• Cover non-continuous domain. For example,
• Is it possible to visit 3 islands in a river with 6
bridges without crossing any bridge more than
once?
• Or, what is the smallest number of telephone
lines needed to connect 200 cities?

5. Logic
• The rules of logic give precise meaning to
mathematical statements.
• These rules are used to distinguish between
valid and invalid mathematical arguments.

6. Statement
• A statement is declarative sentence that is
either true or false, but not the both.
• A statement is also referred as a proposition.

7. Propositional Logic/ Calculus
• The area of logic that deals with propositions is called the propositional
calculus or propositional Logic.
• Example of proposition logic:
– Washington, D.C., is the capital of the United States of America.
– Toronto is the capital of Canada.
– 1 + 1 = 2.
– 2 + 2 = 3.
• Example of not proposition logic
– What time is it?
– Read this carefully.
– x + 1 = 2.
– x + y = z.
• Sentences 1 and 2 are not propositions because they are not declarative
sentences. Sentences 3 and 4 are not propositions because they are
neither true nor false

8. Propositional Variables
• Variables that represent propositions, just as
letters are used to denote numerical variables.
• If a proposition is true, we say that it has a
truth value of “true” and denoted by T.
• If a proposition is false, we say that it has a
truth value of “false” and denoted by F.

9. Compound Proposition
• Many mathematical statements are
constructed by combining (logical operators)
one or more propositions.
• Examples
• “3+2=5” and “Kurukshetra is a city”
• “the grass is green” or “it is raining”
• “Discrete mathematics is a subject not difficult
to me”

10. Compound Propositions
• Negation (not)  p
• Conjunction (and) p  q
• Disjunction (or) p  q
• Exclusive or p  q
• Implication p  q
• Biconditional p  q

11. Negation
• Let p be a proposition. The negation of p,
denoted by￢p (also denoted by p), is the
statement
• “It is not the case that p.”
• The proposition ￢p is read “not p.” The truth
value of the negation of p, ￢p, is the opposite
• of the truth value of p.

12. Example of Negation
• Find the negation of the proposition
“Michael’s PC runs Linux” and express this in
simple English.
• Solution: The negation is “It is not the case
that Michael’s PC runs Linux.”
This negation can be more simply expressed as
“Michael’s PC does not run Linux.”

13. Question
• Find the negation of the proposition
“Vandana’s smartphone has at least 32GB of
memory” and express this in simple English.

14. Conjunction (And)
• Let p and q be propositions. The conjunction of
p and q, denoted by p ∧ q, is the proposition
“p and q.” The conjunction p ∧ q is true when
both p and q are true and is false otherwise.

15. Disjunction
• Let p and q be propositions. The disjunction of
p and q, denoted by p ∨ q, is the proposition
“p or q.” The disjunction p ∨ q is false when
both p and q are false and is true otherwise.

16. Truth Tables
p  p
T
F
p q p  q
p q p  q

17. Reference
• “Discrete mathematics and its applications” by
Kenneth H. Rosen, 7th Edition, TMH.