The document discusses the divide and conquer algorithm design paradigm. It begins by defining divide and conquer as recursively breaking down a problem into smaller sub-problems, solving the sub-problems, and then combining the solutions to solve the original problem. Some examples of problems that can be solved using divide and conquer include binary search, quicksort, merge sort, and the fast Fourier transform algorithm. The document then discusses control abstraction, efficiency analysis, and uses divide and conquer to provide algorithms for large integer multiplication and merge sort. It concludes by defining the convex hull problem and providing an example input and output.

1. Divide and Conquer
Prof. Shashikant V. Athawale
Assistant Professor | Computer Engineering
Department | AISSMS College of Engineering,
Kennedy Road, Pune , MH, India - 411001

2. Contents:
Introduction
Applications
Control Abstraction
Efficiency Analysis
Large Integer Multiplication
Merge Sort
Convex Hull

3. Introduction
Divide and conquer is an algorithm design paradigm
based on multi-branched recursion.
A divide-and-conquer algorithm works by recursively
breaking down a problem into two or more sub-
problems of the same or related type, until these
become simple enough to be solved directly.
The solutions to the sub-problems are then combined
to give a solution to the original problem.

4. Applications
 Binary Search
Quicksort
Merge Sort
Closest Pair of Points
Strassen’s Algorithm
Cooley–Tukey Fast Fourier Transform (FFT)
algorithm
Karatsuba algorithm for fast multiplication

5. Control Abstraction
The meaning of abstractions is preserving
information that is relevant in a given context, and
forgetting information that is irrelevant in that
context.
 Control abstraction: the ability to procedural
data where in the program procedural data is
irrelevant.
A control abstraction is a procedure whose flow
of control is clear but whose basic operations are
defined by other processes whose
meanings/implementations are left undefined.

6. Efficiency Analysis
• Divide and Conquer algorithm solves a problem
using following three steps.
• 1. Divide: Break the given problem into sub-
problems of same type.
2. Conquer: Recursively solve these sub-problems.
3. Combine: Appropriately combine the answers.
• Divide and Conquer algorithm is a very efficient
algorithm.

7. Master’s Theorem
Master’s Theorem is a popular method for solving the
recurrence relations.
Here, a >= 1, b > 1, k >= 0 and p is a real number.

8. Master Theorem Cases-
To solve recurrence relations using Master’s theorem, we compare a with
bk.
 Case-1:
If a > bk, then T(n) = θ (nlog
b
a)
 Case-02:
 If a = bk and
If p < -1, then T(n) = θ (nlog
b
a)
If p = -1, then T(n) = θ (nlog
b
a.log2n)
If p > -1, then T(n) = θ (nlog
b
a.logp+1n)

9. Case-03:
If a < bk and
If p < 0, then T(n) = O (nk)
If p >= 0, then T(n) = θ (nklogpn)

10. Example:
Solve the following recurrence relation using
Master’s theorem-
T(n) = 2T(n/2) + nlogn
 Solution-
We compare the given recurrence relation
with T(n) = aT(n/b) + θ (nklogpn).
Then, we have-
a = 2, b = 2, k = 1, p = 1
Now, a = 2 and bk = 21 = 2.
Clearly, a = bk.
So, we follow case-02.

11. Since p = 1, so we have-
T(n) = θ (nlog
b
a.logp+1n)
T(n) = θ (nlog
2
2.log1+1n)
Thus,
T(n) = θ (nlog2n)

12. Large Integer Multiplication:
Using Divide and Conquer, we can multiply two
integers in less time complexity. We divide the
given numbers in two halves. Let the given
numbers be X and Y.
If a positional numeral system is used, a natural
way of multiplying numbers is taught in schools as
long multiplication, sometimes called grade-
school multiplication, sometimes called Standard
Algorithm: multiply the multiplicand by each digit
of the multiplier and then add up all the properly
shifted results.

13. 1. Grade School Multiplication:
Given two binary strings that represent value of
two integers, find the product of two strings. For
example, if the first bit string is “1100” and second
bit string is “1010”, output should be 120.
For simplicity, let the length of two strings be
same and be n.
A Naive Approach is to follow the process we
study in school. One by one take all bits of second
number and multiply it with all bits of first
number. Finally add all multiplications. This
algorithm takes O(n^2) time.

14. 2. Divide and Conquer
Using Divide and Conquer, we can multiply two
integers in less time complexity. We divide the
given numbers in two halves. Let the given
numbers be X and Y.
For simplicity let us assume that n is even
The product XY can be written as following.
X = Xl*2n/2 + Xr [Xl and Xr contain leftmost and rightmost n/2 bits of X]
Y = Yl*2n/2 + Yr [Yl and Yr contain leftmost and rightmost n/2 bits of Y]
XY = (Xl*2n/2 + Xr)(Yl*2n/2 + Yr)
= 2n XlYl + 2n/2(XlYr + XrYl) + XrYr

15. If we take a look at the above formula, there are four
multiplications of size n/2, so we basically divided the
problem of size n into four sub-problems of size n/2.
But that doesn’t help because solution of recurrence
T(n) = 4T(n/2) + O(n) is O(n^2). The tricky part of this
algorithm is to change the middle two terms to some
other form so that only one extra multiplication would
be sufficient. The following is tricky expression for
middle two terms.
So the final value of XY becomes :
XY = 2n XlYl + 2n/2 * [(Xl + Xr)(Yl + Yr) - XlYl - XrYr] + XrYr

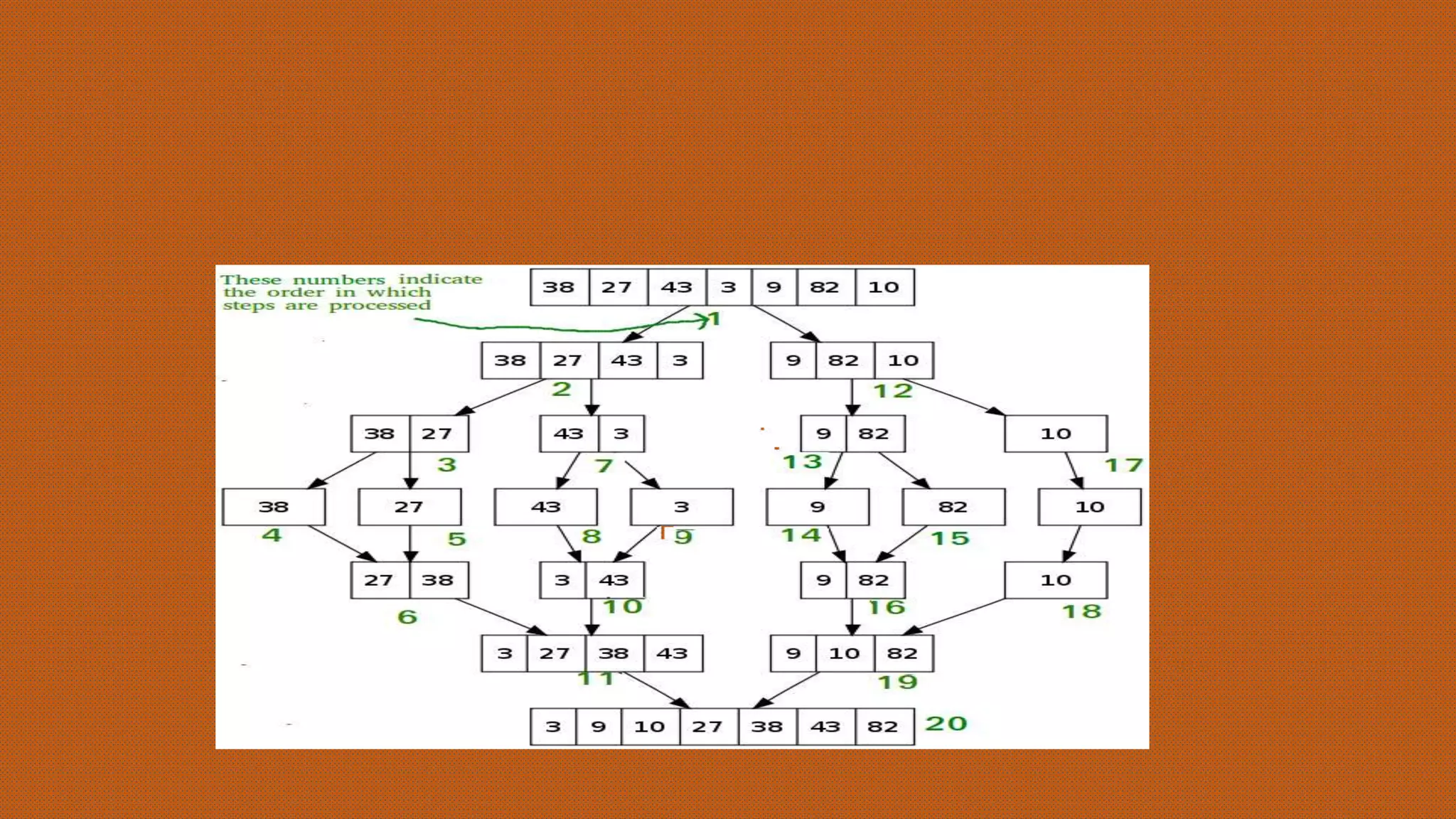
16. Merge Sort
 The merge() function is used for merging two
halves. The merge(arr, l, m, r) is key process that
assumes that arr[l..m] and arr[m+1..r] are sorted
and merges the two sorted sub-arrays into one.
MergeSort(arr[], l, r) If r > l
1. Find the middle point to divide the array into two
halves: middle m = (l+r)/2
2. Call mergeSort for first half: Call mergeSort(arr, l, m)
3. Call mergeSort for second half: Call mergeSort(arr, m+1,
r)
4. Merge the two halves sorted in step 2 and 3:
Call merge(arr, l, m, r)

18. Convex Hull
A convex hull is the smallest convex polygon containing all
the given points.
Input is an array of points specified by their x and y
coordinates. The output is the convex hull of this set of
points.
Input : points[] = {(0, 0), (0, 4), (-4, 0), (5, 0), (0, -6), (1, 0)};
Output : (-4, 0), (5, 0), (0, -6), (0, 4)

19. Thank You.