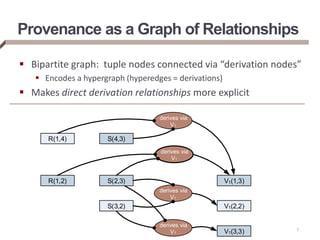
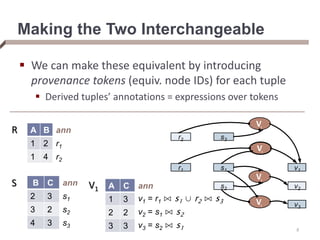
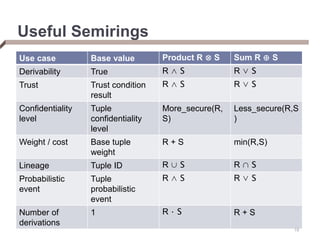
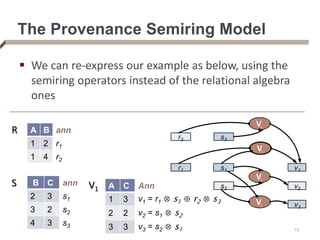
This document discusses data provenance and provides an overview of key concepts: - Data provenance captures the relationships between tuples in integrated data to understand where data came from and how much to trust results. - Provenance can be represented as annotations on tuples or as a graph of relationships. - The provenance semiring model uses algebraic operators to represent provenance in a way that preserves equivalences between queries. - Provenance has applications for explanations, scoring query results, and reasoning about data relationships. 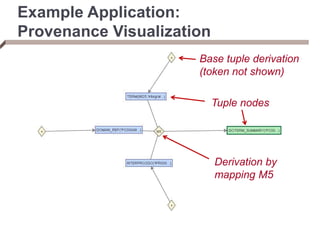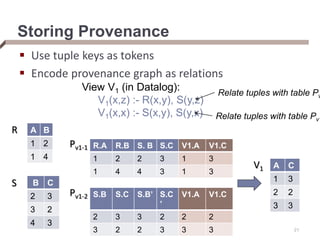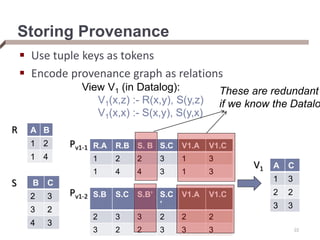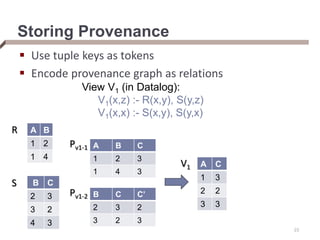- Provenance graphs can be stored relationally using tuple keys as tokens.

1. ANHAI DOAN ALON HALEVY ZACHARY IVES
CHAPTER 14: DATA
PROVENANCE
PRINCIPLES OF
DATA INTEGRATION

2. “Where Did this Data Come from?”
Challenge: integrated data may come from many
sources and mappings – of different quality or
trustworthiness!
 How did I get this particular result?
 What mappings produced it?
 How much should I trust (believe) it?
Data provenance (lineage) captures the relationships
between tuples in a set of data instances
2

3. An Example: View Tuple Derivations
B C
2 3
3 2
4 3
A B
1 2
2 4
R S
Source relations
A C directly derivable by
1 3 R(1,2) ⋈ S(2,3) ∪ R(1,4) ⋈
S(4,3)
2 2 S(2,3) ⋈ ρB  A, C  B S(3,2)
3 3 S(3,2) ⋈ ρB  A, C  B S(2,3)
View V1 = R ⋈ S ∪ S ⋈ S
3

4. Formulating a Provenance Model
Conceptually, provenance captures the operations
and operands going into a result
There are many options to do this, and many levels of detail!
A “good” provenance model should:
 Have a formal semantics
 Have equivalence properties such that equivalent query
plans produce equivalent provenance
 Connect to notions of value, quality or score
4

5. Outline
 The two views of provenance
 Applications of data provenance
 Provenance semirings: one ring to rule them all
 Storing provenance
5

6. Provenance as Annotations on Data
 Annotate each derivation with an “explanation” in
terms of relational algebra and the tuple operands
 Lets us “look up” the derivation of a result
B C
2 3
3 2
4 3
A B
1 2
1 4
R
S
A C provenance annotation
1 3 R(1,2) ⋈ S(2,3) ∪ R(1,4) ⋈
S(4,3)
2 2 S(2,3) ⋈ ρB  A, C  B S(3,2)
3 3 S(3,2) ⋈ ρB  A, C  B S(2,3)
View V1 (in Datalog):
V1(x,z) :- R(x,y), S(y,z)
V1(x,x) :- S(x,y), S(y,x)
6

7. Provenance as a Graph of Relationships
 Bipartite graph: tuple nodes connected via “derivation nodes”
 Encodes a hypergraph (hyperedges = derivations)
 Makes direct derivation relationships more explicit
7
R(1,2)
R(1,4)
S(2,3)
S(3,2)
S(4,3)
V1(1,3)
V1(2,2)
V1(3,3)
derives via
V1
derives via
V1
derives via
V1
derives via
V1

8. Making the Two Interchangeable
 We can make these equivalent by introducing
provenance tokens (equiv. node IDs) for each tuple
 Derived tuples’ annotations = expressions over tokens
B C ann
2 3 s1
3 2 s2
4 3 s3
A B ann
1 2 r1
1 4 r2
R
S A C ann
1 3 v1 = r1 ⋈ s1 ∪ r2 ⋈ s3
2 2 v2 = s1 ⋈ s2
3 3 v3 = s2 ⋈ s1 8
V1
r1
r2
s1
s2
s3
v1
v2
v3
V1
V1
V1
V1

9. Outline
 The two views of provenance
 Applications of data provenance
 Provenance semirings: one ring to rule them all
 Storing provenance
9

10. Where Can We Use Provenance?
Explanations
 Help the user understand why an item exists
Scoring
 Provide a ranked list of “most relevant” results
Reasoning about interactions
 Help the user understand data relationships

11. Examples of Provenance’s Utility
Schema mapping debugging:
We may have a bad result
Determine why that result exists, what is faulty
Bioinformatics data integration:
Different sources have different levels of reliability or
authoritativeness
Rank results by score!
Probabilistic databases:
We may need to know that results are correlated
Encode the relationships, use to assign probabilities

12. Outline
 The two views of provenance
 Applications of data provenance
 Provenance semirings: one ring to rule them all
 Storing provenance
12

13. The Notion of Provenance as
Annotations
 Many formalisms were defined for using query
computations to produce annotations
 Each captured certain subtleties
 The key question: Is there one “most powerful”
model that captures the properties of the relational
algebra*?
 Equivalent queries should produce equivalent provenance
* over multi-sets or bags, as used by “real” systems

14. The Provenance Semiring Model
To represent provenance, use:
 A set of provenance tokens or tuple IDs, K
 Abstract operators representing combination of tuples
Abstract sum operator, ⊕, for union or projection
has identity element 0 (a ⊕ 0 ≡ 0 ⊕ a ≡ 0)
Abstract product operator, ⊗, for join
 has identity element 1 (a ⊗ 1 ≡ 1 ⊗ a ≡ 1)
 also (a ⊗ 0 ≡ 0 ⊗ a ≡ 0)
This is formally a commutative semiring
14

15. The Provenance Semiring Model
 We can re-express our example as below, using the
semiring operators instead of the relational algebra
ones
B C ann
2 3 s1
3 2 s2
4 3 s3
A B ann
1 2 r1
1 4 r2
R
S A C Ann
1 3 v1 = r1 ⊗ s1 ⊕ r2 ⊗ s3
2 2 v2 = s1 ⊗ s2
3 3 v3 = s2 ⊗ s1 15
V1
r1
r2
s1
s2
s3
v1
v2
v3
V1
V1
V1
V1

16. Tokens for Mappings
 Sometimes we would like to assign a token to the actual
mapping or rule used – so we can assign it a value
B C ann
2 3 s1
3 2 s2
4 3 s3
A B ann
1 2 r1
1 4 r2
R
S A C Ann
1 3 v1 = m1⊗ [r1 ⊗ s1] ⊕ m2⊗ [r2 ⊗
s3]
2 2 v2 = m2⊗ [s1 ⊗ s2]
3 3 v3 = m2⊗ [s2 ⊗ s1] 16
V1
View V1 (in Datalog):
V1(x,z) :- R(x,y), S(y,z)
V1(x,x) :- S(x,y), S(y,x)
Call this m1
Call this m2

17. Example Application:
Provenance Visualization
Base tuple derivation
(token not shown)
Tuple nodes
Derivation by
mapping M5

18. Example Application: Tuple
Scoring
 For ranked query results, we may adopt the following model
commonly used in ranking:
 Assign a score to each base tuple = - log2(probability)
 Use arithmetic sum as ⊗
 Use min as ⊕
 Suppose
 prob(r1) = 0.5, prob(s1) = 0.5, others are 1.0
A C Ann
1 3 v1 = r1 ⊗ s1 ⊕ r2 ⊗ s3 = min((2+1),(1+1)) = 2
2 2 v2 = s1 ⊗ s2 = 2+1 = 3
3 3 v3 = s2 ⊗ s1 = 1+2 = 3
V1

19. Useful Semirings
Use case Base value Product R ⊗ S Sum R ⊕ S
Derivability True R ∧ S R ∨ S
Trust Trust condition
result
R ∧ S R ∨ S
Confidentiality
level
Tuple
confidentiality
level
More_secure(R,
S)
Less_secure(R,S
)
Weight / cost Base tuple
weight
R + S min(R,S)
Lineage Tuple ID R ∪ S R ∩ S
Probabilistic
event
Tuple
probabilistic
event
R ∧ S R ∨ S
Number of
derivations
1 R ⋅ S R + S
19

20. Outline
 The two views of provenance
 Applications of data provenance
 Provenance semirings: one ring to rule them all
 Storing provenance
20

21. Storing Provenance
 Use tuple keys as tokens
 Encode provenance graph as relations
B C
2 3
3 2
4 3
A B
1 2
1 4
R
S
A C
1 3
2 2
3 3
V1
View V1 (in Datalog):
V1(x,z) :- R(x,y), S(y,z)
V1(x,x) :- S(x,y), S(y,x)
Relate tuples with table Pv
Relate tuples with table Pv1
R.A R.B S. B S.C V1.A V1.C
1 2 2 3 1 3
1 4 4 3 1 3
S.B S.C S.B’ S.C
’
V1.A V1.C
2 3 3 2 2 2
3 2 2 3 3 3 21
Pv1-1
Pv1-2

22. Storing Provenance
 Use tuple keys as tokens
 Encode provenance graph as relations
B C
2 3
3 2
4 3
A B
1 2
1 4
R
S
A C
1 3
2 2
3 3
V1
View V1 (in Datalog):
V1(x,z) :- R(x,y), S(y,z)
V1(x,x) :- S(x,y), S(y,x)
R.A R.B S. B S.C V1.A V1.C
1 2 2 3 1 3
1 4 4 3 1 3
S.B S.C S.B’ S.C
’
V1.A V1.C
2 3 3 2 2 2
3 2 2 3 3 3 22
Pv1-1
Pv1-2
These are redundant
if we know the Datalo

23. Storing Provenance
 Use tuple keys as tokens
 Encode provenance graph as relations
B C
2 3
3 2
4 3
A B
1 2
1 4
R
S
A C
1 3
2 2
3 3
V1
View V1 (in Datalog):
V1(x,z) :- R(x,y), S(y,z)
V1(x,x) :- S(x,y), S(y,x)
A B C
1 2 3
1 4 3
B C C’
2 3 2
3 2 3
23
Pv1-1
Pv1-2

24. Data Provenance Wrap-up
 Provenance is critical to understanding and assessing
the believability of data, and in debugging
 Two equivalent representations – annotations vs graph
 Provenance semiring model preserves the “expected”
equivalences of the relational algebra
 We can take semiring provenance and evaluate it with
different semirings to get useful scores
 We can store provenance using relations
 Recent work beyond the scope of the book:
 Extending provenance to more complex queries, e.g., with
aggregation
 Languages for querying provenance (primarily as a graph)