More Related Content
PDF
PDF
PPTX
PDF
PPTX
PDF
CoqのInductiveでは定義できないinductive型の公理的な定義する方法 PDF
有限オートマトンとスティッカー系に関するCoqによる形式証明について PPTX
More from Masaki Hara
PDF
You won't know it's now Rust PDF
How I Contribute to Rust Compiler PDF
PDF
Proving Decidability of Intuitionistic Propositional Calculus on Coq PPTX
PPTX
PPTX
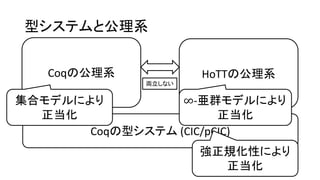
joi2012-sp-day2-broadcasting Coqの公理
- 1.
- 2.
- 3.
- 4.
- 5.
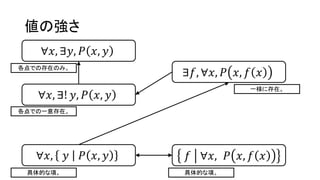
値の強さ
∀𝑥, ∃𝑦, 𝑃𝑥, 𝑦
∀𝑥, ∃! 𝑦, 𝑃 𝑥, 𝑦
∀𝑥, 𝑦 𝑃 𝑥, 𝑦 𝑓 ∀𝑥, 𝑃 𝑥, 𝑓 𝑥
∃𝑓, ∀𝑥, 𝑃 𝑥, 𝑓 𝑥
各点での存在のみ。
各点での一意存在。
一様に存在。
具体的な項。 具体的な項。
- 6.
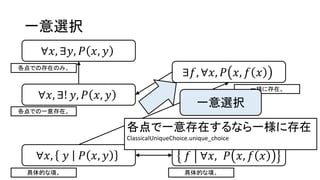
一意選択
∀𝑥, ∃𝑦, 𝑃𝑥, 𝑦
∀𝑥, ∃! 𝑦, 𝑃 𝑥, 𝑦
∀𝑥, 𝑦 𝑃 𝑥, 𝑦 𝑓 ∀𝑥, 𝑃 𝑥, 𝑓 𝑥
∃𝑓, ∀𝑥, 𝑃 𝑥, 𝑓 𝑥
各点での存在のみ。
各点での一意存在。
一様に存在。
具体的な項。 具体的な項。
一意選択
各点で一意存在するなら一様に存在
ClassicalUniqueChoice.unique_choice
- 7.
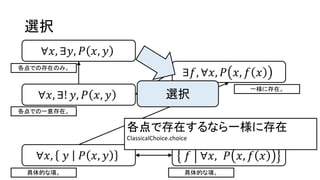
選択
∀𝑥, ∃𝑦, 𝑃𝑥, 𝑦
∀𝑥, ∃! 𝑦, 𝑃 𝑥, 𝑦
∀𝑥, 𝑦 𝑃 𝑥, 𝑦 𝑓 ∀𝑥, 𝑃 𝑥, 𝑓 𝑥
∃𝑓, ∀𝑥, 𝑃 𝑥, 𝑓 𝑥
各点での存在のみ。
各点での一意存在。
一様に存在。
具体的な項。 具体的な項。
選択
各点で存在するなら一様に存在
ClassicalChoice.choice
- 8.
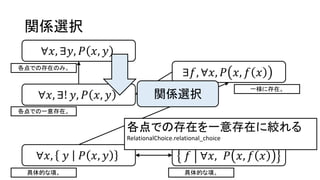
関係選択
∀𝑥, ∃𝑦, 𝑃𝑥, 𝑦
∀𝑥, ∃! 𝑦, 𝑃 𝑥, 𝑦
∀𝑥, 𝑦 𝑃 𝑥, 𝑦 𝑓 ∀𝑥, 𝑃 𝑥, 𝑓 𝑥
∃𝑓, ∀𝑥, 𝑃 𝑥, 𝑓 𝑥
各点での存在のみ。
各点での一意存在。
一様に存在。
具体的な項。 具体的な項。
関係選択
各点での存在を一意存在に絞れる
RelationalChoice.relational_choice
- 9.
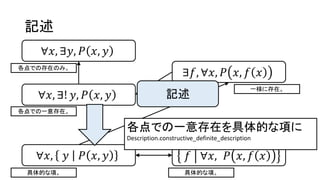
記述
∀𝑥, ∃𝑦, 𝑃𝑥, 𝑦
∀𝑥, ∃! 𝑦, 𝑃 𝑥, 𝑦
∀𝑥, 𝑦 𝑃 𝑥, 𝑦 𝑓 ∀𝑥, 𝑃 𝑥, 𝑓 𝑥
∃𝑓, ∀𝑥, 𝑃 𝑥, 𝑓 𝑥
各点での存在のみ。
各点での一意存在。
一様に存在。
具体的な項。 具体的な項。
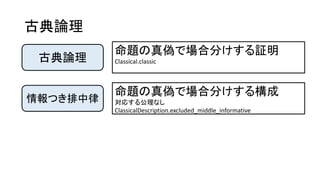
記述
各点での一意存在を具体的な項に
Description.constructive_definite_description
- 10.
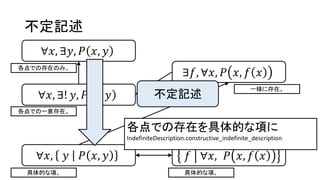
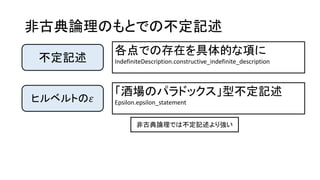
不定記述
∀𝑥, ∃𝑦, 𝑃𝑥, 𝑦
∀𝑥, ∃! 𝑦, 𝑃 𝑥, 𝑦
∀𝑥, 𝑦 𝑃 𝑥, 𝑦 𝑓 ∀𝑥, 𝑃 𝑥, 𝑓 𝑥
∃𝑓, ∀𝑥, 𝑃 𝑥, 𝑓 𝑥
各点での存在のみ。
各点での一意存在。
一様に存在。
具体的な項。 具体的な項。
不定記述
各点での存在を具体的な項に
IndefiniteDescription.constructive_indefinite_description
- 11.
- 12.