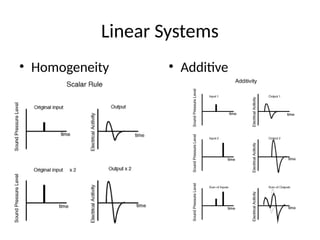
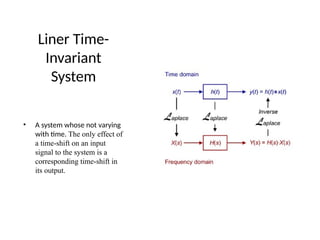
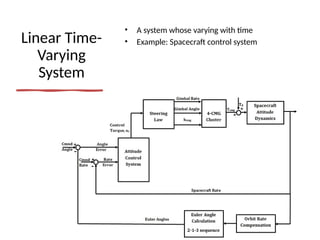
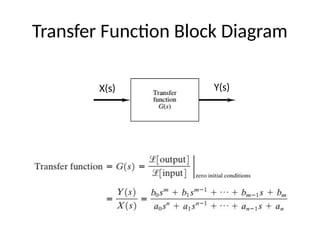
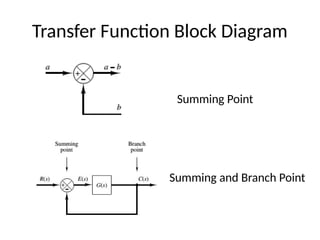
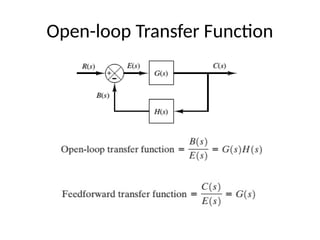
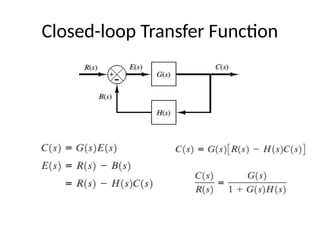
This document covers mathematical modeling in control systems, explaining that a mathematical model consists of equations that describe a system's input-output behavior. It distinguishes between linear and time-varying systems and introduces transfer functions, illustrating concepts with diagrams. Additionally, it outlines homework assignments based on the textbook by Ogata to reinforce these concepts.

1. Sistem Kendali
Week 1
Session 3

2. Mathematical Modeling
What is
mathematical
model?
A set of mathematical
equations (e.g.,
differential eqs.) that
describes the input-
output behavior of a
system.
What is a
model used
for?
• Simulation
• Prediction/
Forecasting
• Prognostics/
Diagnostics
• Design/
Performance
Evaluation
• Control
System
Design

3. Linear Systems
• A system is called linear if the
principle of superposition
applies.
• Systems that satisfy both
homogeneity and additive are
considered to be linear systems

4. Linear Systems
• Homogeneity • Additive

5. Liner Time-
Invariant
System
• A system whose not varying
with time. The only effect of
a time-shift on an input
signal to the system is a
corresponding time-shift in
its output.

6. Linear Time-
Varying
System
• A system whose varying with time
• Example: Spacecraft control system

7. Transfer Function
• Transfer function is defined as the
ratio of the Laplace Transform of the
output to the Laplace Transform of the
input under assumption that all initial
conditions are zero

8. Laplace
Transform
Table

9. Transfer Function Block Diagram
X(s) Y(s)

10. Transfer Function
Block Diagram
• Transfer function is defined as
the ratio of the Laplace
Transform of the output to the
Laplace Transform of the input
under assumption that all initial
conditions are zero
• Summing Point. The plus or
minus sign at each arrowhead
indicates whether that signal is
to be added or subtracted
• Branching Point. A branch point
is a point from which the signal
from a block goes concurrently to
other blocks or summing points

11. Transfer Function Block Diagram
Summing Point
Summing and Branch Point

12. Open-loop Transfer Function

13. Closed-loop Transfer Function

14. Homework 01
Textbook Ogata:
• Problems B-2-1
• Problems B-2-2
• Problems B-2-3
• Problems B-2-5
• Problems B-2-6
• Problems B-2-7
Format A4 Paper; Hand-writing

15. Next Week
• Study Example 2-1
• Impulse response
• Modeling in state space
• Representation of State Space
• Linearization