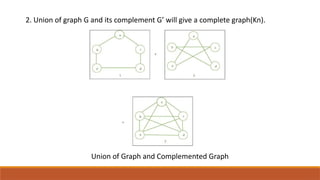
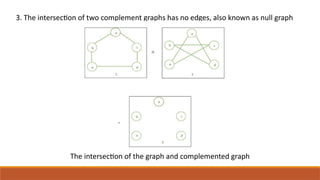
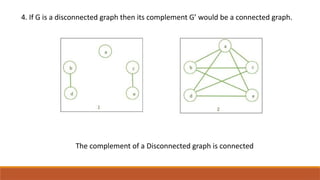
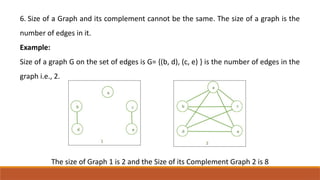
The document discusses the concept of the complement of a graph in graph theory, emphasizing its importance in understanding relationships and properties between graph structures. It outlines key properties of graph complements, such as connectivity changes and edge relationships, along with specific examples. The conclusion highlights the complement's role as a tool for studying graph isomorphisms and combinatorial challenges.

1. Complement of graph
Presented By: Supervisor:
Khadija H.Nasir Dr.Didar A.Ali
Jilan N.Sediq
College of Science
Department of Mathematics

2. Contents
•Introduction
•Properties
•Examples
•Conclusion

3. Introduction
In graph theory, the complement of a graph is an important concept used to explore relationships
between graph structures and their properties. Given a simple graph G=(V,E), where V is the set of
vertices and E is the set of edges, the complement of G, denoted as or is a graph on the same vertex
set V, but with a different edge set.
The edge set of the complement includes all the edges that are not present in G. In other words:
 Two vertices in G′G'G′ are adjacent if and only if they are not adjacent in GGG.
The complement is a tool for studying properties of graphs and their relationships, often used in
applications such as network theory, optimization, and combinatorial problems.

4. Properties of Complement of Graph
1. If E be the set of edges of graph G’ then E(G’)={ (u, v) | (u, v) ∉
E(G) }
Graph and its Complement

5. 2. Union of graph G and its complement G’ will give a complete graph(Kn).
Union of Graph and Complemented Graph

6. 3. The intersection of two complement graphs has no edges, also known as null graph
The intersection of the graph and complemented graph

7. 4. If G is a disconnected graph then its complement G’ would be a connected graph.
The complement of a Disconnected graph is connected

8. 5. Order of a Graph and its Complement are Same. The order of the graph is the number
of vertices in it.
Example:
Order of a graph G on a set of vertices is given by G={a, b, c, d, e} is number of vertices in
the graph G i.e., 5.
The order of Graph 1 and its complement 2 is the same.

9. 6. Size of a Graph and its complement cannot be the same. The size of a graph is the
number of edges in it.
Example:
Size of a graph G on the set of edges is G= {(b, d), (c, e) } is the number of edges in the
graph i.e., 2.
The size of Graph 1 is 2 and the Size of its Complement Graph 2 is 8

10. Examples
Example 1: In this example, we have a simple graph , which contains edges and
10 vertices. Now we will find out the number of edges in the graph .
Solution: From the question, we have the following details about graph :
Number of vertices
Number of edges
As we know that

11. Now we will put the values of n and in this formula, and get the following
details:

12. Consider a simple graph , where denotes the edges and denotes the vertices , . Find =?
Solution:
We know,
Therefore, and
Since vertices cannot be negative
Example 1:

13. Conclusion
The concept of the complement of a graph is a fundamental tool in graph theory,
offering a dual perspective on the structure and relationships within a graph. By
inverting the adjacency relationships of the original graph, the complement
reveals insights into connectivity, independence, and complementary graph
properties. It serves as a powerful tool for exploring graph isomorphisms, self-
complementarity, and combinatorial problems.