![2SAURABH SINGH
1. MOTIVATION
15/10/2013
- Column Liquid Chromatography (CLC)
- Applications in separation sciences e.g. protein separation
CHROMATOGRAPHIC MODEL SOLVER CADET-CS
Packed Bed
[Tallarek et al]](https://image.slidesharecdn.com/cadet-cs-180219062452/85/Column-Liquid-Chromatography-3-320.jpg)
Uploaded bySaurabh Singh
Column Liquid Chromatography
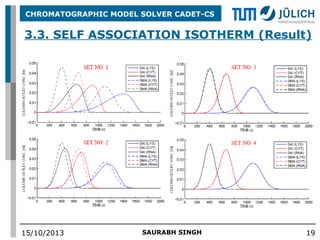
The document describes extensions made to the CADET-CS chromatography model solver. Radial discretization was improved using a higher order WENO scheme, achieving second order convergence. A surface diffusion model was added, increasing the bandwidth of the Jacobian matrix. A self-association isotherm model was also included to model protein dimerization. Sensitivity analysis was performed using algorithmic differentiation for accuracy. An experimental design study used Monte Carlo simulation to determine optimal experiments for parameter estimation under measurement noise.
Column Liquid Chromatography
- 1. Extending the ModelLibrary and Improving Numerical Aspects of the Chromatography Model Solver CADET-CS SAURABH SINGH
- 2. CHROMATOGRAPHIC MODEL SOLVERCADET-CS 1SAURABH SINGH OVERVIEW 15/10/2013 1. MOTIVATION 2. THEORY 3. TASKS & RESULTS 3.1. RADIAL DISCRETIZATIONS 3.2. SURFACE DIFFUSION MODEL 3.3. SELF ASSOCIATION ISOTHERM (SAI) MODEL 3.4. SENSITIVITY ANALYSIS 3.5. EXPERIMENTAL DESIGN STUDY 4. CONCLUSION
- 3. 2SAURABH SINGH 1. MOTIVATION 15/10/2013 -Column Liquid Chromatography (CLC) - Applications in separation sciences e.g. protein separation CHROMATOGRAPHIC MODEL SOLVER CADET-CS Packed Bed [Tallarek et al]
- 4. 2SAURABH SINGH 1. MOTIVATION 15/10/2013 -Column Liquid Chromatography (CLC) - Applications in separation sciences e.g. protein separation CHROMATOGRAPHIC MODEL SOLVER CADET-CS © Metrohm AG
- 5. 3SAURABH SINGH 2. THEORY:MODEL 15/10/2013 - The General Rate Model COLUMN MODEL CHROMATOGRAPHIC MODEL SOLVER CADET-CS
- 6. 3SAURABH SINGH15/10/2013 - TheGeneral Rate Model COLUMN MODEL PARTICLE MODEL CHROMATOGRAPHIC MODEL SOLVER CADET-CS 2. THEORY: MODEL
- 7. 3SAURABH SINGH15/10/2013 - TheGeneral Rate Model COLUMN MODEL PARTICLE MODEL SORPTION MODEL CHROMATOGRAPHIC MODEL SOLVER CADET-CS 2. THEORY: MODEL
- 8. 3SAURABH SINGH15/10/2013 - TheGeneral Rate Model COLUMN MODEL PARTICLE MODEL SORPTION MODEL CHROMATOGRAPHIC MODEL SOLVER CADET-CS 2. THEORY: MODEL
- 9. 4SAURABH SINGH 2. THEORY:APPROACH 15/10/2013 - Finite Volume Method (FVM) Mass Conservation - BDF Scheme Stiff Equations - WENO Scheme Godunov’s Order Barrier Theorem CHROMATOGRAPHIC MODEL SOLVER CADET-CS Exact Solution 2 Points FD 4 Points FD WENO
- 10. 5SAURABH SINGH 2. THEORY:DISCRETE MODEL 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS Components Column Particle Boundary STATE VECTOR
- 11. 5SAURABH SINGH 2. THEORY:DISCRETE MODEL 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS Components Column Particle Boundary STATE VECTOR
- 12. 5SAURABH SINGH 2. THEORY:DISCRETE MODEL 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS Components Column Particle Boundary STATE VECTORJACOBIAN MATRIX How is the sparsity of the Jacobian?
- 13. 6SAURABH SINGH 3.1. RADIALDISCRETIZATIONS 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS - What is Radial Discretization?
- 14. 7SAURABH SINGH 3.1. RADIALDISCRETIZATIONS 15/10/2013 - Depends on the Number and Distribution of nodes CHROMATOGRAPHIC MODEL SOLVER CADET-CS
- 15. 8SAURABH SINGH 3.1. RADIALDISCRETIZATIONS (Results) 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS - Residual is estimated by comparing coarse grid with finer grid
- 16. 9SAURABH SINGH 3.1. RADIALDISCRETIZATIONS (Results) 15/10/2013 - Residual is estimated by comparing coarse grid with finer grid CHROMATOGRAPHIC MODEL SOLVER CADET-CS
- 17. 10SAURABH SINGH 3.1. RADIALDISCRETIZATIONS (Results) 15/10/2013 - Residual decreases linearly & achieves a second order convergence CHROMATOGRAPHIC MODEL SOLVER CADET-CS
- 18. 11SAURABH SINGH 3.1. RADIALDISCRETIZATIONS (Results) 15/10/2013 - Benchmarked on a single core of JuRoPA - Computational endeavour is directly proportional to the grid size CHROMATOGRAPHIC MODEL SOLVER CADET-CS
- 19. 12SAURABH SINGH 3.2. SURFACEDIFFUSION MODEL 15/10/2013 - What is Surface Diffusion? CHROMATOGRAPHIC MODEL SOLVER CADET-CS
- 20. 12SAURABH SINGH 3.2. SURFACEDIFFUSION MODEL 15/10/2013 - Pore Diffusion Model + Surface Diffusion Model CHROMATOGRAPHIC MODEL SOLVER CADET-CS
- 21. 12SAURABH SINGH 3.2. SURFACEDIFFUSION MODEL 15/10/2013 - Pore Diffusion Model + Surface Diffusion Model CHROMATOGRAPHIC MODEL SOLVER CADET-CS PORE DIFFUSION SURFACE DIFFUSION
- 22. 13SAURABH SINGH 3.2. SURFACEDIFFUSION MODEL (Results) 15/10/2013 - Bandwidth of Jacobian increased due to coupling CHROMATOGRAPHIC MODEL SOLVER CADET-CS PARTICLE JACOBIAN (PORE) PORE DIFFUSION ISOTHERM
- 23. 13SAURABH SINGH 3.2. SURFACEDIFFUSION MODEL (Results) 15/10/2013 - Bandwidth of Jacobian increased due to coupling CHROMATOGRAPHIC MODEL SOLVER CADET-CS PARTICLE JACOBIAN (PORE) PARTICLE JACOBIAN (PORE + SURFACE) PORE DIFFUSION SURFACE DIFFUSIONISOTHERM
- 24. 13SAURABH SINGH 3.2. SURFACEDIFFUSION MODEL (Results) 15/10/2013 - Bandwidth of Jacobian increased due to coupling CHROMATOGRAPHIC MODEL SOLVER CADET-CS PARTICLE JACOBIAN (PORE) PARTICLE JACOBIAN (PORE + SURFACE) PORE DIFFUSION SURFACE DIFFUSIONISOTHERM
- 25. 14SAURABH SINGH 3.2. SURFACEDIFFUSION MODEL (Results) 15/10/2013 - Validation of Surface Diffusion Model was challenging! CHROMATOGRAPHIC MODEL SOLVER CADET-CS
- 26. 14SAURABH SINGH 3.2. SURFACEDIFFUSION MODEL (Results) 15/10/2013 - Validation of Surface Diffusion Model was challenging! - Literature suggested the following: 1.) Surface Diffusion Model is a form of Pore Diffusion 2.) Surface Diffusion Coefficient is 2-3 orders of magnitude lower than Pore Diffusion Coefficient - The Surface Diffusion Model was then validated by formulating a parameter estimation problem CHROMATOGRAPHIC MODEL SOLVER CADET-CS
- 27. 15SAURABH SINGH 3.2. SURFACEDIFFUSION MODEL (Results) 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS - Numerical studies with SCL and LWE benchmark examples confirmed the result SCL Benchmark Example
- 28. 15SAURABH SINGH 3.2. SURFACEDIFFUSION MODEL (Results) 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS - Numerical studies with SCL and LWE benchmark examples confirmed the result
- 29. 16SAURABH SINGH 3.3. SELFASSOCIATION ISOTHERM 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS - What is Self Association Isotherm Model? - A Isotherm Model describes the behavior of how macromolecules bind or adsorb to the particle surfaces - Self Association Isotherm (SAI) Model attempts to model the case where a protein molecule associates with an adsorbed molecule - Simplifying by reparametrizing, led to
- 30. 17SAURABH SINGH 3.3. SELFASSOCIATION ISOTHERM 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS - Understanding the process of dimerization
- 31. 17SAURABH SINGH 3.3. SELFASSOCIATION ISOTHERM 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS - Understanding the process of dimerization
- 32. 17SAURABH SINGH 3.3. SELFASSOCIATION ISOTHERM 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS - Understanding the process of dimerization
- 33. - Validation ofSAI Model was another challenging task! 18SAURABH SINGH 3.3. SELF ASSOCIATION ISOTHERM (Result) 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS
- 34. - Validation ofSAI Model was another challenging task! - Comparison of SAI Model was carried out with SMA Model - SAI essentially differs from SMA by a single non-linear term 18SAURABH SINGH15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS 3.3. SELF ASSOCIATION ISOTHERM (Result)
- 35. 19SAURABH SINGH15/10/2013 CHROMATOGRAPHIC MODELSOLVER CADET-CS 3.3. SELF ASSOCIATION ISOTHERM (Result)
- 36. 19SAURABH SINGH15/10/2013 CHROMATOGRAPHIC MODELSOLVER CADET-CS 3.3. SELF ASSOCIATION ISOTHERM (Result)
- 37. 20SAURABH SINGH 3.4. SENSITIVITYANALYSIS 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS - Sensitivities are partial derivatives of time-dependent state vector y with respect to specific model parameters pi
- 38. 20SAURABH SINGH 3.4. SENSITIVITYANALYSIS 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS - Sensitivities are partial derivatives of time-dependent state vector y with respect to specific model parameters pi
- 39. 21SAURABH SINGH 3.4. SENSITIVITYANALYSIS 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS - How to compute sensitivities? Δp = 10-1 Δp = 10-6 ALGORITHMIC DIFFERENTIATION (AD)FINITE DIFFERENCES (FD)
- 40. 21SAURABH SINGH 3.4. SENSITIVITYANALYSIS 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS - How to compute sensitivities? ALGORITHMIC DIFFERENTIATION (AD)FINITE DIFFERENCES (FD) Δp = 10-1 Δp = 10-6 Why is FD not good?
- 41. 22SAURABH SINGH 3.4. SENSITIVITYANALYSIS (Results) 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS
- 42. 23SAURABH SINGH 3.5. EXPERIMENTALDESIGN STUDY 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS - Often, the measured results/data have noise or error associated with them - Task is to examine how error propagates through the model QUESTIONS 1.) What is the optimal design of an experiment from which only one isotherm parameter (qm or keq) can be estimated most accurately? 2.) What is the optimal design of an experiment from which both isotherm parameters (qm and keq) can be (simultaneously) estimated most accurately? - Used Monte Carlo Method - Idea is repeated calculations of input parameter(s), each time perturbing the input data with specific statistical distribution
- 43. 24SAURABH SINGH 3.5. EXPERIMENTALDESIGN STUDY (Result) 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS
- 44. 24SAURABH SINGH 3.5. EXPERIMENTALDESIGN STUDY (Result) 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS
- 45. 25SAURABH SINGH 3.5. EXPERIMENTALDESIGN STUDY (Result) 15/10/2013 CHROMATOGRAPHIC MODEL SOLVER CADET-CS
- 46. 26SAURABH SINGH 4. CONCLUSION 15/10/2013 CHROMATOGRAPHICMODEL SOLVER CADET-CS - CADET-CS is a fast and accurate solver for the General Rate Model of Column Liquid Chromatography - The thesis aimed at extending several aspects of the solver - Future work and further extensions possible: Incorporate the contribution of temperature (Energy Transport) Chemical Reaction can also be incorporated (Chemical Transport) From application viewpoint, be able to model a complex network or configuration of chromatographic columns in series or parallel
- 47. 27SAURABH SINGH REFERENCES 15/10/2013 CHROMATOGRAPHIC MODELSOLVER CADET-CS - von Lieres, E.; Andersson, J.: A fast and accurate solver for the general rate model of column liquid chromatography, Computers and Chemical Engineering 34,8 (2010), 1180–1191. - Saurabh Singh: Extending the Model Library and Improving Numerical Aspects of the Chromatography Model Solver CADET-CS, Master's Thesis, Juelich Forschungzentrum & Technische Universitaet Muenchen, June 2012. - Püttmann, A.; Schnittert, S.; Naumann, U.; von Lieres, E.: Fast and accurate parameter sensitivities for the general rate model of column liquid chromatography, Computers and Chemical Engineering 56,13 (2013), 46-57.
- 48.
Editor's Notes
- #10 Essentially non-osciallatory (ENO) and Weighted ENO (WENO) are finite difference or finite volume schemes. ENO and WENO schemes are designed for problems with piecewise smooth solutions containing discontinuities A key idea in WENO schemes is a linear combination of lower order fluxes or reconstruction to obtain a higher order approximation. Both schemes use the idea of adaptive stencils to automatically achieve high order accuracy and non-oscillatory property near discontinuities.
- #13 Substructuring/Reordering of the state vector is done Yellow Block has a band structure with k subdiagonal and (k-1) superdiagonals, where k is the minimal order of the WENO scheme Orange Blocks also have band structure with 2Nc subdiagonals and superdiagonals Green are off the diagonals and are very sparse
- #38 An alternative to FD is to solve a DAE system for the senitivities. This system can be derived from the original DAE system by differentiating w.r.t to model parameter Staggered Corrector Approach is implemented. In such an approach, the original DAE system and the sensitivity DAE system are solved one after another in each time integration step. AD is implemented via operator overloading for only the parameter derivatives and is realized using ADOL-C tapeless forward implementation in vector mode. Remember: adoubles and NUMBER_DIRECTIONS
- #39 An alternative to FD is to solve a DAE system for the senitivities. This system can be derived from the original DAE system by differentiating w.r.t to model parameter. Staggered Corrector Approach is implemented. In such an approach, the original DAE system and the sensitivity DAE system are solved one after another in each time integration step. AD is implemented via operator overloading for only the parameter derivatives and is realized using ADOL-C tapeless forward implementation in vector mode. Remember: adoubles and NUMBER_DIRECTIONS
- #40 An alternative to FD is to solve a DAE system for the senitivities. This system can be derived from the original DAE system by differentiating w.r.t to model parameter Staggered Corrector Approach is implemented. In such an approach, the original DAE system and the sensitivity DAE system are solved one after another in each time integration step. AD is implemented via operator overloading for only the parameter derivatives and is realized using ADOL-C tapeless forward implementation in vector mode. Remember: adoubles and NUMBER_DIRECTIONS
- #41 An alternative to FD is to solve a DAE system for the senitivities. This system can be derived from the original DAE system by differentiating w.r.t to model parameter Staggered Corrector Approach is implemented. In such an approach, the original DAE system and the sensitivity DAE system are solved one after another in each time integration step. AD is implemented via operator overloading for only the parameter derivatives and is realized using ADOL-C tapeless forward implementation in vector mode. Remember: adoubles and NUMBER_DIRECTIONS
- #43 1. Each time perturbing the input data (i.e. column outlet conc.) with a specific statistical distribution and then observing the effect on the output parameter(s). 2. In order to test for the effect of noise, heteroscedastic random noise levels ranging from 1%, 5%, and 10% of the minimum concentration flow rate were added to the chromatograms
- #44 1. Each time perturbing the input data (i.e. column outlet conc.) with a specific statistical distribution and then observing the effect on the output parameter(s). 2. In order to test for the effect of noise, heteroscedastic random noise levels ranging from 1%, 5%, and 10% of the minimum concentration flow rate were added to the chromatograms
- #45 1. Each time perturbing the input data (i.e. column outlet conc.) with a specific statistical distribution and then observing the effect on the output parameter(s). 2. In order to test for the effect of noise, heteroscedastic random noise levels ranging from 1%, 5%, and 10% of the minimum concentration flow rate were added to the chromatograms
- #46 1. Each time perturbing the input data (i.e. column outlet conc.) with a specific statistical distribution and then observing the effect on the output parameter(s). 2. In order to test for the effect of noise, heteroscedastic random noise levels ranging from 1%, 5%, and 10% of the minimum concentration flow rate were added to the chromatograms