Mai Hoài, profile picture
Uploaded byMai Hoài
PPT, PDF293 views

Chg1 xs k38

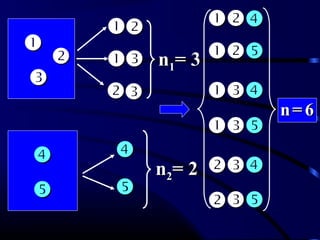
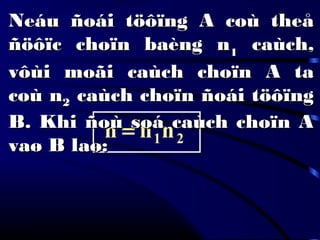
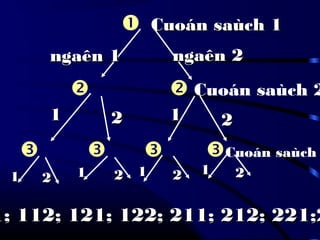
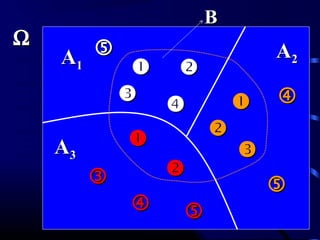
Tài liệu trình bày về lý thuyết xác suất trong toán học, gồm nhiều phần từ việc xác suất của biến cố đến các công thức tính toán liên quan. Ngoài ra, tài liệu cũng đề cập đến các kiểu kiểm tra và đánh giá trong quá trình học tập, bao gồm điểm quá trình và điểm thi kết thúc học phần. Các phần lý thuyết và bài tập được xây dựng để giúp người học hiểu rõ hơn về ứng dụng của xác suất trong thực tế.

Embed presentation

Download to read offline
1 / 155
2 / 155
3 / 155
4 / 155
5 / 155
6 / 155
7 / 155
8 / 155
9 / 155
10 / 155
11 / 155
12 / 155
13 / 155
14 / 155
15 / 155
16 / 155
17 / 155
18 / 155
19 / 155
20 / 155
21 / 155
22 / 155
23 / 155
24 / 155
25 / 155
26 / 155
27 / 155
28 / 155
29 / 155
30 / 155
31 / 155
32 / 155
33 / 155
34 / 155
35 / 155
36 / 155
37 / 155
38 / 155
39 / 155
40 / 155
41 / 155
42 / 155
43 / 155
44 / 155
45 / 155
46 / 155
47 / 155
48 / 155
49 / 155
50 / 155
51 / 155
52 / 155
53 / 155
54 / 155
55 / 155
56 / 155
57 / 155
58 / 155
59 / 155
60 / 155
61 / 155
62 / 155
63 / 155
64 / 155
65 / 155
66 / 155
67 / 155
68 / 155
69 / 155
70 / 155
71 / 155
72 / 155
73 / 155
74 / 155
75 / 155
76 / 155
77 / 155
78 / 155
79 / 155
80 / 155
81 / 155
82 / 155
83 / 155
84 / 155
85 / 155
86 / 155
87 / 155
88 / 155
89 / 155
90 / 155
91 / 155
92 / 155
93 / 155
94 / 155
95 / 155
96 / 155
97 / 155
98 / 155
99 / 155
100 / 155
101 / 155
102 / 155
103 / 155
104 / 155
105 / 155
106 / 155
107 / 155
108 / 155
109 / 155
110 / 155
111 / 155
112 / 155
113 / 155
114 / 155
115 / 155
116 / 155
117 / 155
118 / 155
119 / 155
120 / 155
121 / 155
122 / 155
123 / 155
124 / 155
125 / 155
126 / 155
127 / 155
128 / 155
129 / 155
130 / 155
131 / 155
132 / 155
133 / 155
134 / 155
135 / 155
136 / 155
137 / 155
138 / 155
139 / 155
140 / 155
141 / 155
142 / 155
143 / 155
144 / 155
145 / 155
146 / 155
147 / 155
148 / 155
149 / 155
150 / 155
151 / 155
152 / 155
153 / 155
154 / 155
155 / 155
GVGV HOAØNG NGOÏCHOAØNG NGOÏC NHAÄMNHAÄM Boä moân:Boä moân: TOAÙNTOAÙN KINH TEÁKINH TEÁ Khoa:Khoa: TOAÙN -TOAÙN - THOÁNG KEÂTHOÁNG KEÂ
Phaàn IPhaàn I LYÙ THUYEÁT XAÙCLYÙ THUYEÁT XAÙC SUAÁTSUAÁT
Chöông 1Chöông 1 Xaùc suaát cuûa bieánXaùc suaát cuûa bieán coácoá vaø caùc coâng thöùc tínhvaø caùc coâng thöùc tính xaùc suaátxaùc suaátChöông 2Chöông 2 Ñaïi löôïng ngaãu nhieânÑaïi löôïng ngaãu nhieân vaø phaân phoái xaùcvaø phaân phoái xaùc suaátsuaát
Chöông 3Chöông 3 Moät soá phaân phoáiMoät soá phaân phoái xaùc suaát thoâng duïngxaùc suaát thoâng duïng Chöông 4Chöông 4 Ñaïi löôïng ngaãu nhieânÑaïi löôïng ngaãu nhieân hai chieàu – haøm cuûahai chieàu – haøm cuûa caùc ñaïi löôïngcaùc ñaïi löôïng
Chöông 6Chöông 6 Maãu ngaãu nhieânMaãu ngaãu nhieân Phaàn IIPhaàn II THOÁNG KEÂTHOÁNG KEÂ TOAÙNTOAÙN Chöông 5Chöông 5 Luaät soá lôùnLuaät soá lôùn vaø caùc ñònh lyù giôùivaø caùc ñònh lyù giôùi haïnhaïn
Chöông 8Chöông 8 Kieåm ñònh giaû thieátKieåm ñònh giaû thieát thoáng keâthoáng keâ Chöông 7Chöông 7 Öôùc löôïng caùc tham soáÖôùc löôïng caùc tham soá ñaëcñaëc tröng cuûa ñaïi löôïngtröng cuûa ñaïi löôïng ngaãu nhieânngaãu nhieân
1-1- Lyù thuyeát xaùc suaátLyù thuyeát xaùc suaát & thoáng keâ toaùn.& thoáng keâ toaùn. Hoaøng NgoïcHoaøng Ngoïc NhaämNhaäm NXB Kinh t TP H Chíế ồNXB Kinh t TP H Chíế ồ TAØI LIEÄU HOÏC TAÄPTAØI LIEÄU HOÏC TAÄP VAØ THAM KHAÛOVAØ THAM KHAÛO
3-3- Baøi taäp xaùc suaátBaøi taäp xaùc suaát thoáng keâthoáng keâ Th s Hoaøng NgoïcTh s Hoaøng Ngoïc Nhaäm,Nhaäm, 2-2- Giaùo trình lyù thuyeátGiaùo trình lyù thuyeát xaùc suaát & thoáng keâxaùc suaát & thoáng keâ toaùn hoïctoaùn hoïc Ths Traàn Gia TuøngThs Traàn Gia Tuøng NXB ÑH Quoác gia TP Hoà ChíNXB ÑH Quoác gia TP Hoà Chí Minh, 2009Minh, 2009
Cách đánh giá:Cách đánh giá: - Điểm quá trình: 30%;- Điểm quá trình: 30%; - Điểm thi kết thúc HP: 70%- Điểm thi kết thúc HP: 70% - Điểm quá trình bao gồm:- Điểm quá trình bao gồm: điểm kiểm tra giữa kỳ,điểm kiểm tra giữa kỳ, điểm thảo thuận, sửa bài tậpđiểm thảo thuận, sửa bài tập trên lớptrên lớp, . . .. . .
Bài kiểm tra giữa kỳ: Thời gian: 45 phút. Nội dung: phần xác suất. Bài thi kết thúc học phần: Thôøi gian 75 Phuùt. Coù hai phaàn: Phaàn I: traéc nghieäm Phaàn II: tự luận
PHAÀN I Chöông 1Chöông 1 LYÙ THUYEÁT XAÙCLYÙ THUYEÁT XAÙC SUAÁTSUAÁT XAÙC SUAÁT CUÛA BIEÁNXAÙC SUAÁT CUÛA BIEÁN COÁ VAØ CAÙCCOÁ VAØ CAÙC COÂNG THÖÙC TÍNH XAÙCCOÂNG THÖÙC TÍNH XAÙC SUAÁTSUAÁTI- Pheùp thöû, bieán coá,I- Pheùp thöû, bieán coá, khoâng giankhoâng gian
Caùc thí duCaùc thí duï:ï:  Tung (gieo) moät ñoàngTung (gieo) moät ñoàng xu.xu.  Tung (gieo) moät conTung (gieo) moät con suùc saéc.suùc saéc.  Choïn ngaãu nhieân 2Choïn ngaãu nhieân 2 saûn phaåm töø kieänsaûn phaåm töø kieän haøng coù 5 saûn phaåmhaøng coù 5 saûn phaåm ñeå kieåm tra.ñeå kieåm tra.
 Quan saùt ñieåm thiQuan saùt ñieåm thi moân toaùn cao caáp cuûamoân toaùn cao caáp cuûa moät sinh vieân heä CQ.moät sinh vieân heä CQ.  Laøm caùc thí nghieämLaøm caùc thí nghieäm ñeå nghieân cöùu veàñeå nghieân cöùu veà naêng suaát cuûa moätnaêng suaát cuûa moät gioáng luùa môùi.gioáng luùa môùi.
•• Pheùp thöû laø moät thí nghieäm hay quan saùt. •• Pheùp thöû laø nhöõng coâng vieäc, nhöõng haønh ñoäng cuûa con ngöôøi nhaèm quan saùt, nghieân cöùu moät hieän töôïng, moät ñoái töôïng
Khi thöïc hieän moät pheùp thöû coù nhieàu keát quaû coù theå xaûy ra. Coù keát quaû ñôn giaûn, coù keát quaû phöùc hôïp.
Khi tung moät con suùcKhi tung moät con suùc saéc, suùc saéc ra maëtsaéc, suùc saéc ra maët 1 chaám, 2 chaám, . . . ,1 chaám, 2 chaám, . . . , 6 chaám laø nhöõng6 chaám laø nhöõng keát quaû ñôn giaûn,keát quaû ñôn giaûn, suùc saéc ra maëtsuùc saéc ra maët chaün, suùc saéc rachaün, suùc saéc ra
Keát quaû ñôn giaûnKeát quaû ñôn giaûn nhaát ñöôïc goïi laønhaát ñöôïc goïi laø bieán coá sô caápbieán coá sô caáp Taäp hôïp taát caû caùcTaäp hôïp taát caû caùc bieán coá sô caáp ñöôïcbieán coá sô caáp ñöôïc goïi laøgoïi laø khoâng giankhoâng gian caùc bieán coá sôcaùc bieán coá sô caápcaáp (khoâng gian(khoâng gian
•• Moãi taäp con cuûaMoãi taäp con cuûa khoâng gian maãu ñöôïckhoâng gian maãu ñöôïc goïi laøgoïi laø bieán coábieán coá..•• Bieán coá laø moätBieán coá laø moät keát quaû coù theå xaûykeát quaû coù theå xaûy ra khi thöïc hieänra khi thöïc hieän pheùp thöû.pheùp thöû.•• Khoâng gian caùcKhoâng gian caùc bieán coá sô caáp kyùbieán coá sô caáp kyù
Gieo moät con suùc saécGieo moät con suùc saéc ωi (i = 1, 2, . . . , 6) chæ(i = 1, 2, . . . , 6) chæ keát quaû suùc saéc xuaátkeát quaû suùc saéc xuaát hieän maët i chaám.hieän maët i chaám. Thí duï 1:   Ω = {ω1 , ω2 , ω3 , ω4 , ω5 , ω6 }
Thí duï 2: Kieåm tra 1Kieåm tra 1 saûn phaåm choïn ngaãusaûn phaåm choïn ngaãu nhieân töø moät kieännhieân töø moät kieän haøng. Giaû thieát saûnhaøng. Giaû thieát saûn phaåm hoaëc loaïi I,phaåm hoaëc loaïi I, hoaëc loaïi II, hoaëchoaëc loaïi II, hoaëc pheá phaåm.pheá phaåm.   Ω = {ω1 , ω2 , ω3 }
Thí duï 3: Kieåm tra 2Kieåm tra 2 saûn phaåm choïn ngaãusaûn phaåm choïn ngaãu nhieân töø moät kieännhieân töø moät kieän haøng. Giaû thieát saûnhaøng. Giaû thieát saûn phaåm hoaëc loaïi I,phaåm hoaëc loaïi I, hoaëc loaïi II, hoaëchoaëc loaïi II, hoaëc pheá phaåm.pheá phaåm. Khoâng gian caùc bieán coá sôKhoâng gian caùc bieán coá sô caáp goàm coù caùc phaàn töûcaáp goàm coù caùc phaàn töû naøo ?naøo ?
spsp11 spsp22 LoaïiLoaïi II LoaïiLoaïi IIII LoaïiLoaïi PPPP LoaïiLoaïi II LoaïiLoaïi IIII LoaïiLoaïi PPPP            Ω = {ω1 , ω2 , . . . , ω }
Chuù yù: Caùc bieán coá cuï theåCaùc bieán coá cuï theå luoân gaén lieàn vôùiluoân gaén lieàn vôùi pheùp thöû cuï theå.pheùp thöû cuï theå. PhePhe ùpùp KhoâKhoâ ngng giangian caùccaùc BieáBieá nn
Pheùp thöûPheùp thöûKh. gian maãuKh. gian maãu Bieán coáBieán coá Tung 1Tung 1 ñoàng xuñoàng xu ΩΩ = {H, C}= {H, C} XHXH maët hình (H)maët hình (H) XHXH maët chöõ (C)maët chöõ (C). Tung 1Tung 1 concon suùcsuùc saécsaéc Ω = {= {ωω11,, ωω22,, . . . ,. . . , ωω66}} XH maët 3, 6,XH maët 3, 6, XH maët chaün,XH maët chaün, . . .. . . Kieåm traKieåm tra 1 saûn1 saûn phaåmphaåm Ω == {{ωω11,, ωω22,, ωω33}} SP laø loaïi I,SP laø loaïi I, SP laø loaïi II,SP laø loaïi II, SP laø pheá phaåmSP laø pheá phaåm
 Bieán coá ngaãuBieán coá ngaãu nhieânnhieân A, B, C, D, E,A, B, C, D, E, F, . . .F, . . .  Bieán coá chaécBieán coá chaéc chaén (chaén (Ω)  Bieán coá khoângBieán coá khoâng theå (theå (∅))
ÑònhÑònh nghóa 1nghóa 1:: Bieán coá A ñöôïc goïi laøBieán coá A ñöôïc goïi laø keùo theo bieán coá B,keùo theo bieán coá B, kyù hieäu laøkyù hieäu laø AA ⊂⊂ BB neáuneáu A xaûy ra thì B cuõngA xaûy ra thì B cuõng xaûy ra.xaûy ra. II- MOÁI QUAN HEÄ GIÖÕA CAÙCII- MOÁI QUAN HEÄ GIÖÕA CAÙC BIEÁN COÁBIEÁN COÁ
Thí duïThí duï:: Tung moät con suùcTung moät con suùc saéc, goïi A laø bieánsaéc, goïi A laø bieán coá “suùc saéc ra maëtcoá “suùc saéc ra maët 2” vaø B laø bieán coá2” vaø B laø bieán coá “suùc saéc ra maët“suùc saéc ra maët chaün” thì:chaün” thì:
ÑònhÑònh nghóa 2nghóa 2:: Bieán coá A vaø B ñöôïcBieán coá A vaø B ñöôïc goïi laø haigoïi laø hai bieán coábieán coá töông ñöôngtöông ñöông,, kyù hieäukyù hieäu laølaø A = BA = B neáu Aneáu A ⊂⊂ BB vaø Bvaø B ⊂⊂ A.A.Neáu A = B thì: P(A) =Neáu A = B thì: P(A) = P(B)P(B)
Thí duïThí duï:: Kieåm tra 2 saûnKieåm tra 2 saûn phaåm. Goïi A laøphaåm. Goïi A laø bieán coá “coù ít nhaátbieán coá “coù ít nhaát moät pheá phaåm” vaømoät pheá phaåm” vaø B laø bieán coá “coù 1B laø bieán coá “coù 1 pheá phaåm hoaëc coùpheá phaåm hoaëc coù
CaâuCaâu hoûihoûi::Taïi sao xaùc suaátTaïi sao xaùc suaát cuûa caùc bieán coácuûa caùc bieán coá töông ñöông laïi baèngtöông ñöông laïi baèng nhau ?nhau ?
Toång cuûa 2 bieán coá AToång cuûa 2 bieán coá A vaø B laø moät bieán coá,vaø B laø moät bieán coá, kyù hieäu laøkyù hieäu laø AA ∪∪ BB (hoaëc(hoaëc A + BA + B). Bieán coá naøy). Bieán coá naøy xaûy ra khi vaø chæ khixaûy ra khi vaø chæ khi coù ít nhaát moät trong haicoù ít nhaát moät trong hai bieán coá A, B xaûy ra.bieán coá A, B xaûy ra. ÑònhÑònh nghóa 3nghóa 3::
Thí duïThí duï:: Quan saùt 2 xaï thuû cuøngQuan saùt 2 xaï thuû cuøng baén vaøo moät bia. Moãibaén vaøo moät bia. Moãi xaï thuû baén moät vieân.xaï thuû baén moät vieân. Goïi A laø bieán coá “Goïi A laø bieán coá “xaïxaï thuû thöù nhaát baénthuû thöù nhaát baén truùng biatruùng bia”, B laø bieán”, B laø bieán coá “coá “xaï thuû thöù haixaï thuû thöù hai
Ñònh nghóaÑònh nghóa 44:: Tích cuûa hai bieán coá ATích cuûa hai bieán coá A vaø B laø moät bieán coá,vaø B laø moät bieán coá, kkyù hieäu laø Ayù hieäu laø A ∩∩ BB ((hoaëc AB), bieán coáhoaëc AB), bieán coá naøy xaûy ra khi vaø chænaøy xaûy ra khi vaø chæ khi caû A vaø B xaûy ra.khi caû A vaø B xaûy ra.
Thí duïThí duï:: Xeùt pheùp thöû quan saùtXeùt pheùp thöû quan saùt hai xaï thuû cuøng baén vaøohai xaï thuû cuøng baén vaøo moät bia (moãi ngöôøi baénmoät bia (moãi ngöôøi baén moät vieân). Goïi A laø bieánmoät vieân). Goïi A laø bieán coá “coá “xaï thuû thöù nhaátxaï thuû thöù nhaát baén traätbaén traät”, B laø bieán coá”, B laø bieán coá ““xaï thuû thöù hai baénxaï thuû thöù hai baén traättraät” vaø C laø bieán coá “” vaø C laø bieán coá “
Ñònh nghóaÑònh nghóa 55:: Hai bieán coá A vaø BHai bieán coá A vaø B ñöôïc goïi laø xungñöôïc goïi laø xung khaéc neáu Akhaéc neáu A∩∩B =B = ∅∅.. A, B laø 2 bieán coáA, B laø 2 bieán coá xung khaéc neáu chuùngxung khaéc neáu chuùng khoâng theå ñoàngkhoâng theå ñoàng thôøi xaûy ra khi thöïcthôøi xaûy ra khi thöïc
Chuù yùïChuù yùï:: A, B laø 2 bieán coáA, B laø 2 bieán coá khoâng xung khaéckhoâng xung khaéc neáu chuùng coù theåneáu chuùng coù theå ñoàng thôøi xaûy ra khiñoàng thôøi xaûy ra khi thöïc hieän pheùpthöïc hieän pheùp thöûù.thöûù.
Thí duï 1Thí duï 1:: Kieåm tra 2 saûnKieåm tra 2 saûn phaåm. Goïi A laøphaåm. Goïi A laø bieán coá “coù 1 pheábieán coá “coù 1 pheá phaåm”. B laø bieánphaåm”. B laø bieán coá “khoâng coù pheácoá “khoâng coù pheá phaåm” thì A, B laø 2phaåm” thì A, B laø 2
Thí duï 2Thí duï 2:: Kieåm tra 3 saûnKieåm tra 3 saûn phaåm. Goïi A laøphaåm. Goïi A laø bieán coá “saûn phaåmbieán coá “saûn phaåm thöù nhaát laø saûnthöù nhaát laø saûn phaåm toát; B laø bieánphaåm toát; B laø bieán coá saûn phaåm thöùcoá saûn phaåm thöù
Ñònh nghóaÑònh nghóa 66:: Bieán coá ñoái laäpBieán coá ñoái laäp vôùi bieán coá A, kyùvôùi bieán coá A, kyù hieäu laø A, neáu A, Ahieäu laø A, neáu A, A xung khaéc vaø Axung khaéc vaø A∪∪A =A = ΩΩ.. Bieán coá “ khoângBieán coá “ khoâng xaûy ra bieán coá A”xaûy ra bieán coá A” ñöôïc goïi laø bieán coáñöôïc goïi laø bieán coá
Thí duïThí duï:: Kieåm tra 5 saûnKieåm tra 5 saûn phaåm. Goïi A laøphaåm. Goïi A laø bieán coá “coù ít nhaátbieán coá “coù ít nhaát 3 saûn phaåm toát”. A3 saûn phaåm toát”. A laø bieán coá “soálaø bieán coá “soá saûn phaåm toátsaûn phaåm toát
Bieåu ñoàBieåu ñoà VENNVENN:: Quan saùt 2 xaï thuû cuøngQuan saùt 2 xaï thuû cuøng baén vaøo moät bia. Moãibaén vaøo moät bia. Moãi xaï thuû baén moät vieân.xaï thuû baén moät vieân. Goïi A laø bieán coá “Goïi A laø bieán coá “xaïxaï thuû thöù nhaát baénthuû thöù nhaát baén truùng biatruùng bia”, B laø bieán”, B laø bieán coá “coá “xaï thuû thöù haixaï thuû thöù hai baén truùng biabaén truùng bia”, C laø”, C laø
ΩΩ AA     BB  AA ∪∪ BB
Quan saùt 2 xaï thuû cuøngQuan saùt 2 xaï thuû cuøng baén vaøo moät bia. Moãibaén vaøo moät bia. Moãi xaï thuû baén moät vieân.xaï thuû baén moät vieân. Goïi A laø bieán coá “Goïi A laø bieán coá “xaïxaï thuû thöù nhaát baénthuû thöù nhaát baén traättraät”, B laø bieán coá “”, B laø bieán coá “xaïxaï thuû thöù hai baén traätthuû thöù hai baén traät”,”, C laø bieán coá “C laø bieán coá “bia khoângbia khoâng truùng ñaïntruùng ñaïn”.”.
ΩΩ AA     BB  AA ∩∩ BB
Quan saùt 2 xaï thuû cuøngQuan saùt 2 xaï thuû cuøng baén vaøo moät bia. Moãibaén vaøo moät bia. Moãi xaï thuû baén moät vieân.xaï thuû baén moät vieân. Goïi A laø bieán coá “Goïi A laø bieán coá “coùcoù moät vieân truùngmoät vieân truùng”, B laø”, B laø bieán coá “bieán coá “coù 2 vieâncoù 2 vieân truùngtruùng”, A, B xung khaéc”, A, B xung khaéc
ΩΩ AA     BB  A, B xung khA, B xung khaécaéc
Quan saùt 2 xaï thuû cuøngQuan saùt 2 xaï thuû cuøng baén vaøo moät bia. Moãibaén vaøo moät bia. Moãi xaï thuû baén moät vieân.xaï thuû baén moät vieân. Goïi A laø bieán coá “Goïi A laø bieán coá “coùcoù moät vieân truùngmoät vieân truùng”, thì A”, thì A seõ laø bieán coá “seõ laø bieán coá “coù 2coù 2 vieân truùng hoaëc khoângvieân truùng hoaëc khoâng coù vieân naøo truùngcoù vieân naøo truùng”.”.
ΩΩ AA        Bieán coá ñoái laäpBieán coá ñoái laäp AA
Bieåu ñoàBieåu ñoà VENNVENN::
Caâu hoûi: Kieåm tra 3 saûn phaåmKieåm tra 3 saûn phaåm choïn ngaãu nhieân töøchoïn ngaãu nhieân töø moät kieän haøng. Giaûmoät kieän haøng. Giaû thieát saûn phaåm hoaëcthieát saûn phaåm hoaëc laø ñaït tieâu chuaån hoaëclaø ñaït tieâu chuaån hoaëc khoâng ñaït tieâu chuaån.khoâng ñaït tieâu chuaån. -Khoâng gian maãu coù baoKhoâng gian maãu coù bao nhieâu phaàn töû ? Haõynhieâu phaàn töû ? Haõy
Haõy chæ ra caùc taäp hôïpHaõy chæ ra caùc taäp hôïp bieåu dieãn caùc b/c sau:bieåu dieãn caùc b/c sau: 1-1- Khoâng coù saûn phaåmKhoâng coù saûn phaåm ñaït tieâu chuaån trong 3 spñaït tieâu chuaån trong 3 sp kieåm tra.kieåm tra. 2-2- Coù 1 sp ñaït tieâu chuaånCoù 1 sp ñaït tieâu chuaån trong 3 sp kieåm tra.trong 3 sp kieåm tra. 3-3- Coù 2 sp ñaït tieâu chuaånCoù 2 sp ñaït tieâu chuaån trong 3 sp kieåm tra.trong 3 sp kieåm tra. 4-4- Caû 3 sp k.tra ñeàu ñaïtCaû 3 sp k.tra ñeàu ñaït
            ω1 ω2 ω3 ω4 ω5 ω6 ω7 ω8
Caùc tínhCaùc tính chaátchaát::  A ∪ B = BB = B ∪∪ AA  A ∩ B = BB = B ∩∩ AA  A∪(BB∪∪C) =C) = (A(A∪∪B)B)∪∪CC = A= A ∪∪ BB ∪∪ CC
 A∩(BB∩∩CC) = () = (AA∩∩BB))∩∩CC == AA ∩∩ BB ∩∩ CC A∪(BB∩∩CC)=)= ((AA∪∪BB))∩∩((AA∪∪CC)) A∩(BB∪∪CC)=)= ((AA∩∩BB))∪∪((AA∩∩CC))
BABA ∩=∪ BABA ∪=∩  
1- Khaùi nieäm veà xaùc1- Khaùi nieäm veà xaùc suaát:suaát: Xaùc suaátXaùc suaát cuûa moätcuûa moät bieán coá laø moät con soábieán coá laø moät con soá bieåu thò khaû naêng xaûybieåu thò khaû naêng xaûy ra bieán coá ñoù khi thöïcra bieán coá ñoù khi thöïc
Xeùt pheùp thöûXeùt pheùp thöû ττ, giaû söû, giaû söû khoâng gian maãu coù höõukhoâng gian maãu coù höõu haïn caùc bieán coá sô caáphaïn caùc bieán coá sô caáp vaø caùc bieán coá naøy coùvaø caùc bieán coá naøy coù khaû naêng xaûy ra nhökhaû naêng xaûy ra nhö nhau (ta goïi laø ñoàngnhau (ta goïi laø ñoàng khaû naêng).khaû naêng). 2- Ñònh nghóa coå ñieån2- Ñònh nghóa coå ñieån veà xaùc suaátveà xaùc suaát
Ta noùi ñôn giaûn: n laø soáTa noùi ñôn giaûn: n laø soá tröôøng hôïp ñoàng khaûtröôøng hôïp ñoàng khaû naêng coù theå xaûy ra khinaêng coù theå xaûy ra khi thöïc hieän pheùp thöûthöïc hieän pheùp thöû ττ •• Bieán coá ABieán coá A == AA11∪∪AA22∪∪ .. .. .. ∪∪ AAmm trong ñoù Atrong ñoù Aii ( i = 1, 2, . . . ,( i = 1, 2, . . . , m) laø caùc bieán coá sôm) laø caùc bieán coá sô caáp.caáp. Ta noùi ñôn giaûn: m laø
Khi ñoù, xaùc suaátKhi ñoù, xaùc suaát cuûa bieán coá A, kyùcuûa bieán coá A, kyù hieäu laø P(A), ñöôïchieäu laø P(A), ñöôïc ñònh nghóañònh nghóa laø:laø: P(A)P(A) == mm nn
Thí duïThí duï 11Tung moät con suùcTung moät con suùc saéc caân ñoái vaøsaéc caân ñoái vaø ñoàng chaát.ñoàng chaát.Caùc tröôøng hôïpCaùc tröôøng hôïp ñoàng khaû naêng laø:ñoàng khaû naêng laø: suùc saéc ra maët 1,suùc saéc ra maët 1, suùc saéc ra maët 2, . . .suùc saéc ra maët 2, . . .
Thí duïThí duï 22Choïn ngaãu nhieânChoïn ngaãu nhieân moät sinh vieân töømoät sinh vieân töø moät lôùp coù 50 sinhmoät lôùp coù 50 sinh vieân (trong ñoù coù 30vieân (trong ñoù coù 30 nöõ vaø 20 nam).nöõ vaø 20 nam).
Tröôøng hôïp ñoàngTröôøng hôïp ñoàng khaû naêng laø nhöõngkhaû naêng laø nhöõng tröôøng hôïp naøo?tröôøng hôïp naøo? Bao nhieâu tröôøngBao nhieâu tröôøng hôïp ñoàng khaûhôïp ñoàng khaû naêng?naêng?
Thí duïThí duï 33Choïn ngaãu nhieân 2Choïn ngaãu nhieân 2 saûn phaåm töø moätsaûn phaåm töø moät kieän haøng coù 5 saûnkieän haøng coù 5 saûn phaåm (trong ñoù coù 3phaåm (trong ñoù coù 3 saûn phaåm loaïi I vaøsaûn phaåm loaïi I vaø 2 saûn phaåm loaïi II).2 saûn phaåm loaïi II).
Tröôøng hôïp ñoàngTröôøng hôïp ñoàng khaû naêng laø nhöõngkhaû naêng laø nhöõng tröôøng hôïp naøo?tröôøng hôïp naøo? Bao nhieâu tröôøngBao nhieâu tröôøng hôïp ñoàng khaûhôïp ñoàng khaû naêng?naêng?
                      n = 10n = 10
Thí duïThí duï 11Tung moät con suùc saécTung moät con suùc saéc caân ñoái vaø ñoàng chaát.caân ñoái vaø ñoàng chaát. Goïi A laø b/c suùc saéc raGoïi A laø b/c suùc saéc ra maët chaünmaët chaünCaùc tröôøng hôïp thuaänCaùc tröôøng hôïp thuaän lôïi cho A laø: suùc saéc ralôïi cho A laø: suùc saéc ra maët 2, suùc saéc ra maëtmaët 2, suùc saéc ra maët 4, suùc saéc ra maët 6.4, suùc saéc ra maët 6.
Thí duïThí duï 22Choïn ngaãu nhieânChoïn ngaãu nhieân moät sinh vieân töømoät sinh vieân töø moät lôùp coù 50 sinhmoät lôùp coù 50 sinh vieân (trong ñoù coù 30vieân (trong ñoù coù 30 nöõ vaø 20 nam). Goïinöõ vaø 20 nam). Goïi B laø bieán coá choïnB laø bieán coá choïn
Tröôøng hôïp thuaänTröôøng hôïp thuaän lôïi cho B laø nhöõnglôïi cho B laø nhöõng tröôøng hôïp naøo?tröôøng hôïp naøo? Bao nhieâu tröôøngBao nhieâu tröôøng hôïp thuaän lôïi chohôïp thuaän lôïi cho bieán coá B?bieán coá B?
Thí duïThí duï 33Choïn ngaãu nhieân 2Choïn ngaãu nhieân 2 saûn phaåm töø moätsaûn phaåm töø moät kieän haøng coù 5 saûnkieän haøng coù 5 saûn phaåm (trong ñoù coù 3phaåm (trong ñoù coù 3 saûn phaåm loaïi I vaø 2saûn phaåm loaïi I vaø 2 saûn phaåm loaïi II). Goïisaûn phaåm loaïi II). Goïi C laø bieán coá choïn ñöôïcC laø bieán coá choïn ñöôïc
Tröôøng hôïp thuaänTröôøng hôïp thuaän lôïi cho C laø nhöõnglôïi cho C laø nhöõng tröôøng hôïp naøo?tröôøng hôïp naøo? Bao nhieâu tröôøngBao nhieâu tröôøng hôïphôïp thuaän lôïi cho bieánthuaän lôïi cho bieán coá C?coá C?
              m = 6m = 6
b- Caùc tính chaát cuûab- Caùc tính chaát cuûa xaùc suaát:xaùc suaát:  Neáu A laø b/coá ngaãuNeáu A laø b/coá ngaãu nhieân thì:nhieân thì: 0 < P(A) < 10 < P(A) < 1 NeáuNeáu ΩΩ laø b/coá chaéclaø b/coá chaéc chaén thì:chaén thì: P(P(ΩΩ) = 1) = 1 NeáuNeáu ∅∅ laø b/coá khoânglaø b/coá khoâng theå thì:theå thì: P(P(∅∅) = 0) = 0
Vôùi A laø bieánVôùi A laø bieán coá baátcoá baát kyø, ta luoânkyø, ta luoân coù:coù: 00 ≤≤ P(A)P(A) ≤≤ 11
3- Caùc khaùi nieäm3- Caùc khaùi nieäm cuûa giaûi tích toå hôïpcuûa giaûi tích toå hôïp ** Qui taéc nhaân
ThíThí duïduï:Coù hai hoäp, hoäp thöùCoù hai hoäp, hoäp thöù nhaát coù 3 saûn phaåm,nhaát coù 3 saûn phaåm, hoäp thöù hai coù 2 saûnhoäp thöù hai coù 2 saûn phaåm. Laáy ngaãu nhieânphaåm. Laáy ngaãu nhieân töø hoäp thöù nhaát ra 2töø hoäp thöù nhaát ra 2 saûn phaåm, töø hoäp thöùsaûn phaåm, töø hoäp thöù hai laáy ngaãu nhieân ra 1hai laáy ngaãu nhieân ra 1
        nn11= 3= 3   nn22= 2= 2                 nn == 66
21nnn = Neáu ñoái töôïng A coù theåNeáu ñoái töôïng A coù theå ñöôïc choïn baèng nñöôïc choïn baèng n11 caùch,caùch, vôùi moãi caùch choïn A tavôùi moãi caùch choïn A ta coù ncoù n22 caùch choïn ñoái töôïngcaùch choïn ñoái töôïng B. Khi ñoù soá caùch choïn AB. Khi ñoù soá caùch choïn A vaø B laø:vaø B laø:
Toång quaùt: Neáu choïnNeáu choïn k ñoái töôïng thì soá caùchk ñoái töôïng thì soá caùch choïn k ñoái töôïng seõ laø:choïn k ñoái töôïng seõ laø: k21 n....nnn = (n(nii laø soá caùch choïn ñoáilaø soá caùch choïn ñoái töôïng thöù i )töôïng thöù i )
* Chænh hôïp Chænh hôïp chaäp kChænh hôïp chaäp k cuûa n phaàn töû (kcuûa n phaàn töû (k ≤≤ n) laø moät nhoùm coùn) laø moät nhoùm coù thöù töï goàm k phaànthöù töï goàm k phaàn töû khaùc nhau choïntöû khaùc nhau choïn töø n phaàn töû.töø n phaàn töû.
Soá chænh hôïp chaäpSoá chænh hôïp chaäp k cuûa n phaàn töûk cuûa n phaàn töû ñöôïc kyù hieäu laø:ñöôïc kyù hieäu laø: k nA )!kn( !n Ak n − =
Thí duïThí duï Coù theå thaønh laäpCoù theå thaønh laäp ñöôïc bao nhieâuñöôïc bao nhieâu concon soásoá goàm 3goàm 3 chöõ soáchöõ soá khaùc nhau töø 5 chöõkhaùc nhau töø 5 chöõ soá 1, 2, 3, 4, 5.soá 1, 2, 3, 4, 5.
GiaûGiaû iiMoätMoät con soácon soá goàm 3goàm 3 chöõchöõ soásoá khaùc nhau töø choïnkhaùc nhau töø choïn töø 5 chöõ soá 1, 2, 3, 4, 5töø 5 chöõ soá 1, 2, 3, 4, 5 chaúng haïn nhö: 153; 315;chaúng haïn nhö: 153; 315; 243; . . .243; . . . Coù theå xem nhöCoù theå xem nhö moät chænh hôïp chaäp 3moät chænh hôïp chaäp 3 cuûa 5 phaàn töû.cuûa 5 phaàn töû. Vaäy soáVaäy soá caùc con soá coù theå thaønhcaùc con soá coù theå thaønh33 55
* Chænh hôïp laëp Chænh hôïp laëp chaäp kChænh hôïp laëp chaäp k cuûa n phaàn töû laø moätcuûa n phaàn töû laø moät nhoùm coù thöù töï goàm knhoùm coù thöù töï goàm k phaàn töû choïn töø nphaàn töû choïn töø n phaàn töû. Trong ñoù moãiphaàn töû. Trong ñoù moãi phaàn töû coù theå coùphaàn töû coù theå coù maët (laëp laïi) moät laàn,maët (laëp laïi) moät laàn,
Vì moãi phaàn töû coùVì moãi phaàn töû coù theå coù maët nhieàu laàntheå coù maët nhieàu laàn trong moät chænh hôïptrong moät chænh hôïp laëp neân k coù theå lôùnlaëp neân k coù theå lôùn hôn n cuõng ñöôïc.hôn n cuõng ñöôïc.Soá chænh hôïp laëp chaäpSoá chænh hôïp laëp chaäp k cuûa n phaàn töû ñöôïck cuûa n phaàn töû ñöôïc kyù hieäu laøkyù hieäu laø (hoaëc )(hoaëc ) k n B k nA ~ kk n nB =
ChuùChuù yùyù• Moät chænh hôïp cuõngMoät chænh hôïp cuõng chính laø moät chænh hôïpchính laø moät chænh hôïp laëp (caùc phaàn töû tronglaëp (caùc phaàn töû trong nhoùm laëp laïi toái ña 1nhoùm laëp laïi toái ña 1 laàn).laàn). • Taäp hôïp caùc chænhTaäp hôïp caùc chænh hôïp khoâng laëp laø moäthôïp khoâng laëp laø moät
Thí duïThí duï 11Coù theå thaønh laäpCoù theå thaønh laäp ñöôïc bao nhieâuñöôïc bao nhieâu con soácon soá goàm 2goàm 2 chöõ soáchöõ soá töø 4töø 4 chöõ soá 1, 2, 3, 4.chöõ soá 1, 2, 3, 4.
GiaGia ûiûiVì khoâng ñoøi hoûi 2 soáVì khoâng ñoøi hoûi 2 soá phaûi khaùc nhau, neânphaûi khaùc nhau, neân moãi con soá goàm 2 chöõmoãi con soá goàm 2 chöõ soá choïn töø taäp hôïpsoá choïn töø taäp hôïp goàm 4 chöõ soá: 1, 2, 3, 4,goàm 4 chöõ soá: 1, 2, 3, 4, chaúng haïn nhö: 12; 13;chaúng haïn nhö: 12; 13; 31; 24; 33; . . . coù theå xem31; 24; 33; . . . coù theå xem nhö moät chænh hôïp laëpnhö moät chænh hôïp laëp44 22 22
1212 1313 1414 2121 3131 4141 2323 2424 3232 4242 3434 4343 3333 2222 1111 4444
Thí duïThí duï 22Xeáp 3 cuoán saùch vaøo 2Xeáp 3 cuoán saùch vaøo 2 ngaên. Hoûi coù baongaên. Hoûi coù bao nhieâu caùch xeáp?nhieâu caùch xeáp? GiaûiGiaûi:: -- Xeáp caû 3 cuoánXeáp caû 3 cuoán saùch vaøo ngaên 1. Xem nhösaùch vaøo ngaên 1. Xem nhö choïn 3 soá 1 (choïn 3 soá 1 (111111).).
-Xeáp cuoán 1 vaøo ngaên 2,Xeáp cuoán 1 vaøo ngaên 2, xeáp cuoán 2 vaøo ngaên 1,xeáp cuoán 2 vaøo ngaên 1, xeáp cuoán 3 vaøo ngaên 2:xeáp cuoán 3 vaøo ngaên 2: ((212212)) -Khaùi quaùt:Khaùi quaùt: moãi caùchmoãi caùch xeáp 3 cuoán saùch vaøo 2xeáp 3 cuoán saùch vaøo 2 ngaên xem nhö moät chænhngaên xem nhö moät chænh hôïp laëp chaäp 3 cuûa 2.hôïp laëp chaäp 3 cuûa 2. Vaäy soá caùch xeáp laø:Vaäy soá caùch xeáp laø:22 33 33
CaùchCaùch xeápxeáp ngaên 1ngaên 1 Ngaên 2Ngaên 2 11  111111 22  222222 33   112112 44   112222 55   112121 66   221111 77   222211 88   221212
 Cuoán saùch 1Cuoán saùch 1 ngaên 2ngaên 2ngaên 1ngaên 1   Cuoán saùch 2    Cuoán saùch 2211 2211 11 11 11 11 22 22 22 22 1; 112; 121; 122; 211; 212; 221;21; 112; 121; 122; 211; 212; 221;2
* Hoaùn vò Hoaùn vò cuûa m phaànHoaùn vò cuûa m phaàn töû laø moät nhoùm coùtöû laø moät nhoùm coù thöù töï goàm ñuû maët mthöù töï goàm ñuû maët m phaàn töû.phaàn töû.Soá hoaùn vò cuûa mSoá hoaùn vò cuûa m phaàn töû ñöôïc kyù hieäuphaàn töû ñöôïc kyù hieäu laø Plaø Pmm !mPm =
ChuùChuù yùyùCaùc hoaùn vò ñeàuCaùc hoaùn vò ñeàu gioáng nhau veà thaønhgioáng nhau veà thaønh phaàn, chæ khaùc nhauphaàn, chæ khaùc nhau bôûi thöù töï saép xeápbôûi thöù töï saép xeáp cuûa caùc phaàn töûcuûa caùc phaàn töû trong nhoùm.trong nhoùm.
Thí duïThí duï Xeáp 3 ngöôøi vaøoXeáp 3 ngöôøi vaøo moät daõy gheá 3 choãmoät daõy gheá 3 choã ngoài. Hoûi coù baongoài. Hoûi coù bao nhieâu caùch xeáp?nhieâu caùch xeáp?
GiaûiGiaûi Moãi caùch xeáp 3 ngöôøiMoãi caùch xeáp 3 ngöôøi vaøo moät daõy gheá 3vaøo moät daõy gheá 3 choã ngoài ñeàu gioángchoã ngoài ñeàu gioáng nhau veà thaønh phaàn,nhau veà thaønh phaàn, chæ khaùc nhau bôûi thöùchæ khaùc nhau bôûi thöù töï saép xeáp cuûa caùctöï saép xeáp cuûa caùc phaàn töû trong nhoùm.phaàn töû trong nhoùm.
Caùch xeápCaùch xeáp 11    22    33    44    55    66   
ChuùChuù yùyùCoù theå duøng qui taécCoù theå duøng qui taéc nhaân thay theá chonhaân thay theá cho chænh hôïp, chænhchænh hôïp, chænh hôïp laëp, hoaùn vò.hôïp laëp, hoaùn vò.
* Toå hôïpToå hôïp Toå hôïp chaäp k cuûaToå hôïp chaäp k cuûa n phaàn töû (kn phaàn töû (k ≤≤ n) laøn) laø moät nhoùm khoângmoät nhoùm khoâng phaân bieät thöù töïphaân bieät thöù töï goàm k phaàn töûgoàm k phaàn töû khaùc nhau choïn töø nkhaùc nhau choïn töø n
Soá toå hôïp chaäp kSoá toå hôïp chaäp k cuûa n phaàn töû ñöôïccuûa n phaàn töû ñöôïc kyù hieäu laøkyù hieäu laø k nC )!kn(!k !n Ck n − =
ChuùChuù yùyùToå hôïp vaø chænh hôïpToå hôïp vaø chænh hôïp gioáng nhau ôû choã: ñeàugioáng nhau ôû choã: ñeàu laø nhöõng nhoùm goàm klaø nhöõng nhoùm goàm k phaàn töû khaùc nhau choïnphaàn töû khaùc nhau choïn töø taäp hôïp goàm n phaàntöø taäp hôïp goàm n phaàn töû. Khaùc nhau ôû choã:töû. Khaùc nhau ôû choã: toå hôïp khoâng phaântoå hôïp khoâng phaân bieät thöù töï, chænh hôïpbieät thöù töï, chænh hôïp
Thí duïThí duï 11Moät lôùp trong moätMoät lôùp trong moät hoïc kyø phaûi hoïc 5hoïc kyø phaûi hoïc 5 moân, moãi ngaøy hoïcmoân, moãi ngaøy hoïc 2 moân. Vaäy coù bao2 moân. Vaäy coù bao nhieâu caùch xeáp thôøinhieâu caùch xeáp thôøi khoùa bieåu trong moätkhoùa bieåu trong moät ngaøy?ngaøy?
GiaGia ûiûiKhi xeáp thôøi khoaù bieåuKhi xeáp thôøi khoaù bieåu trong moät ngaøy neáu tatrong moät ngaøy neáu ta thay ñoåi thöù töï moânthay ñoåi thöù töï moân hoïc seõ taïo ra caùch xeáphoïc seõ taïo ra caùch xeáp khaùc. Töùc coù phaânkhaùc. Töùc coù phaân bieät thöù töï moân hoïc.bieät thöù töï moân hoïc. Vaäy moãi caùch xeáp thôøiVaäy moãi caùch xeáp thôøi khoaù bieåu trong moätkhoaù bieåu trong moät55 22
CaùchCaùch xeápxeáp Caùch xeápCaùch xeáp 11  1111  22  1212  33  1313  44  1414  55  1515  66  1616  77  1717  88  1818  99  1919  1010  2020 
Thí duïThí duï 22Coù 5 ñoäi boùng thiCoù 5 ñoäi boùng thi ñaáu vôùi nhau theoñaáu vôùi nhau theo caùch: 2 ñoäi baát kyøcaùch: 2 ñoäi baát kyø trong 5 ñoäi boùngtrong 5 ñoäi boùng naøy phaûi thi ñaáunaøy phaûi thi ñaáu vôùi nhau moät traän.vôùi nhau moät traän. Hoûi phaûi toå chöùcHoûi phaûi toå chöùc
GiaGia ûiûiMoät traän giöõa hai ñoäiMoät traän giöõa hai ñoäi boùng thì khoâng caànboùng thì khoâng caàn phaân bieät thöù töï cuûaphaân bieät thöù töï cuûa hai ñoäi boùng ñoù. Vì vaäyhai ñoäi boùng ñoù. Vì vaäy moät traän ñaáu giöõa 2moät traän ñaáu giöõa 2 ñoäi choïn trong soá 5 ñoäiñoäi choïn trong soá 5 ñoäi boùng laø moät toå hôïpboùng laø moät toå hôïp chaäp 2 cuûa 5. Vaäy soáchaäp 2 cuûa 5. Vaäy soá55 22
SoáSoá tttt SoáSoá tttt 11 ABAB 66 BDBD 22 ACAC 77 BEBE 33 ADAD 88 CDCD 44 AEAE 99 CECE 55 BCBC 1010 DEDE
•Chuù yù: • Ñeå tínhÑeå tính • coù theå duøng caùccoù theå duøng caùc haøm:haøm: • COMBIN(n,k); FACT(m);COMBIN(n,k); FACT(m); • PERMUT(n,k); POWER(n,kPERMUT(n,k); POWER(n,k)) • trong Exceltrong Excel (xem phuï(xem phuï luïc 1)luïc 1) k n k nm k n B;A;P;C
4- Ñònh nghóa thoáng4- Ñònh nghóa thoáng keâ cuûakeâ cuûa xaùc suaátxaùc suaát Xeùt pheùp thöûXeùt pheùp thöû ττ vaøvaø A laø moät bieán coá.A laø moät bieán coá. Giaû söû ta coù theåGiaû söû ta coù theå thöïc hieän laëp laïithöïc hieän laëp laïi pheùp thöûpheùp thöû ττ voâ haïnvoâ haïn
Khi thöïc hieän pheùpKhi thöïc hieän pheùp thöûthöû ττ n laàn ta thaáyn laàn ta thaáy coù k laàn bieán coácoù k laàn bieán coá A xaûy ra, ta goïi tyûA xaûy ra, ta goïi tyû soásoá laø taàn suaát cuûalaø taàn suaát cuûa bieán coá A trong nbieán coá A trong n kk nn
fn(A) = Khi n taêng voâ haïnKhi n taêng voâ haïn taàn suaát ftaàn suaát fnn(A) caøng(A) caøng gaàn moät soá khoânggaàn moät soá khoâng ñoåi p, khi ñoù:ñoåi p, khi ñoù: P(A) = lim fn(A) = p n→∞ n k
Trong thöïc teá, khi nTrong thöïc teá, khi n ñuû lôùn, ta xaáp xæñuû lôùn, ta xaáp xæ P(A)P(A) ≈≈ ffnn(A)(A)Thí duï: 1-1- Tính xaùc suaát ñeåTính xaùc suaát ñeå moät maùy saûn xuaátmoät maùy saûn xuaát ra pheá phaåmra pheá phaåm2-2- Tính xaùc suaát ñeåTính xaùc suaát ñeå xe oâ toâ bò tai naïn.xe oâ toâ bò tai naïn.
IV- Caùc coâng thöùcIV- Caùc coâng thöùc tính xaùc suaáttính xaùc suaát  Neáu A vaø B laø haiNeáu A vaø B laø hai bieán coá xung khaéc thì:bieán coá xung khaéc thì: P(AP(A ∪∪ B) = P(A) +B) = P(A) + P(B)P(B) 1-1- Coâng thöùc coäng xaùcCoâng thöùc coäng xaùc suaátsuaát::
Toång quaùt:    Neáu ANeáu A11, A, A22, . . . , A, . . . , Ann laølaø n bieán coá xung khaécn bieán coá xung khaéc töøng ñoâi, thì:töøng ñoâi, thì: P(AP(A11 ∪∪ AA22 ∪∪ . . .. . . ∪∪ AAnn) =) = P(AP(A11) +) +
Heä quaû:Heä quaû: Neáu A vaøNeáu A vaø laø hai bieán coá ñoái laäplaø hai bieán coá ñoái laäp nhau thì:nhau thì: A P(A) = 1P(A) = 1 −− P( )P( )A
 Neáu A vaø B laø haiNeáu A vaø B laø hai bieán coá khoâng xungbieán coá khoâng xung khaéc thì:khaéc thì:P(AP(A ∪∪ B) = P(A) + P(B)B) = P(A) + P(B) −− P(AB)P(AB) +−−− ++=∪∪ )AA(P)AA(P)AA(P )A(P)A(P)A(P)AAA(P 323121 321321 )AAA(P 321+ Tröôøng hôïp n = 3:Tröôøng hôïp n = 3: NeáuNeáu AA11, A, A22, A, A33 laø caùc b/coálaø caùc b/coá khoâng xung khaéc, thì:khoâng xung khaéc, thì:
Thí duï 1Thí duï 1:: Moät hoäp coù 5 saûn phaåm (trong ñoù coù 3 saûn phaåm loaïi I vaø 2 saûn phaåm loaïi II. Laáy ngaãu nhieân töø hoäp ra 2 saûn phaåm. Tìm xaùc suaát ñeå coù
GiaûiGiaûi:: Goïi AGoïi A00 laø b/claø b/c “khoâng coù saûn phaåm“khoâng coù saûn phaåm loaïi I naøo trong 2 saûnloaïi I naøo trong 2 saûn phaåm laáy ra”; Aphaåm laáy ra”; A11 laø b/claø b/c “coù 1 saûn phaåm loaïi I“coù 1 saûn phaåm loaïi I trong 2 saûn phaåm laáytrong 2 saûn phaåm laáy ra”; A laø b/c”coù khoângra”; A laø b/c”coù khoâng quaù 1 saûn phaåm loaïi Iquaù 1 saûn phaåm loaïi I trong 2 saûn phaåm laáytrong 2 saûn phaåm laáy A = AA = A00 ∪∪ AA11 AA00, A, A11 xung khaéc.xung khaéc.
P(A) = P(AP(A) = P(A00 ∪∪ AA11) = P(A) = P(A00) +) + P(AP(A11)) P(AP(A00) = = = 0,1) = = = 0,1 CC CC 2 22 22 55 11 1010 P(AP(A11) = = =) = = = 0,60,6 CC CC CC 55 33 11 11 22 22 1010 66 ⇒⇒ P(A) = 0,1 + 0,6 =P(A) = 0,1 + 0,6 = 0,70,7
1-1- Xaùc suaáùtXaùc suaáùt coù ñieàu kieäncoù ñieàu kieän 2- Coâng thöùc nhaân2- Coâng thöùc nhaân xaùc suaátxaùc suaát a-a- ÑònhÑònh nghóanghóa::Xaùc suaát cuûa bieán coáXaùc suaát cuûa bieán coá A ñöôïc tính vôùi ñieàuA ñöôïc tính vôùi ñieàu kieän bieán coá B ñaõkieän bieán coá B ñaõ xaûy ra goïi laø xaùcxaûy ra goïi laø xaùc
b-b- Coâng thöùc tínhCoâng thöùc tính:: Ñeå tính xaùc suaát coùÑeå tính xaùc suaát coù ñieàu kieän, tuøy theoñieàu kieän, tuøy theo ñieàu kieän cuï theå cuûañieàu kieän cuï theå cuûa baøi toaùn ta coù theåbaøi toaùn ta coù theå duøng: ñònh nghóa coåduøng: ñònh nghóa coå ñieån, coâng thöùc Bayes,ñieån, coâng thöùc Bayes, hoaëc aùp duïng coânghoaëc aùp duïng coâng
P(A/B)P(A/B) == c- Thí duï:c- Thí duï: Moät lôùp coùMoät lôùp coù 50 s/v (20 nöõ vaø 30 nam,50 s/v (20 nöõ vaø 30 nam, trong ñoù coù 5 nöõ gioûitrong ñoù coù 5 nöõ gioûi toaùn). Gaëp ng.n moät s/vtoaùn). Gaëp ng.n moät s/v cuûa lôùp. Tìm xaùc suaátcuûa lôùp. Tìm xaùc suaát P(AB)P(AB) P(B)P(B)
GiaûiGiaûi:: Goïi A laø bieánGoïi A laø bieán coá “gaëp ñöôïc s/v gioûicoá “gaëp ñöôïc s/v gioûi toaùn”; B laø bieán coátoaùn”; B laø bieán coá “gaëp ñöôïc s/v nöõ”. Ta“gaëp ñöôïc s/v nöõ”. Ta caàn tìm P(A/B).caàn tìm P(A/B). P(A/B)P(A/B) == P(AB)P(AB) P(BP(B )) == 5/5/ 505020/520/5 00 == 0,250,25
Hai bieán coá A, B ñöôïcHai bieán coá A, B ñöôïc goïi laø ñoäc laäp vôùigoïi laø ñoäc laäp vôùi nhau neáu:nhau neáu: P(A/B) = P(A)P(A/B) = P(A) HoaëcHoaëc P(B/A) = P(B)P(B/A) = P(B)Vieäc xaûy ra hay khoângVieäc xaûy ra hay khoâng xaûy ra cuûa b/c naøyxaûy ra cuûa b/c naøy khoâng aûnh höôûng ñeánkhoâng aûnh höôûng ñeán
Hai bieán coá A, BHai bieán coá A, B ñöôïc goïi laø ñoäcñöôïc goïi laø ñoäc laäp vôùi nhau khilaäp vôùi nhau khi vaø chæ khi:vaø chæ khi: P(AB) =P(AB) = P(A).P(B)P(A).P(B)
Neáu A, B ñoäc laäpNeáu A, B ñoäc laäp thì:thì: A, B; A, B vaø A, BA, B; A, B vaø A, B cuõng ñoäc laäp.cuõng ñoäc laäp.
Caùc b/c ACaùc b/c A11, A, A22, . . . A, . . . Ann ñöôïc goïi laø ñoäc laäpñöôïc goïi laø ñoäc laäp toaøn phaàn neáu moãitoaøn phaàn neáu moãi b/c ñoäc laäp vôùi moätb/c ñoäc laäp vôùi moät toå hôïp baát kyø trongtoå hôïp baát kyø trong caùc bieán coá coøn laïi.caùc bieán coá coøn laïi.
Neáu A, B laø hai b/cNeáu A, B laø hai b/c baát kyø thì:baát kyø thì: P(AB) =P(AB) = P(A).P(B/A)P(A).P(B/A) == P(B).P(A/B)P(B).P(A/B) 2-2- Ñònh lyù:Ñònh lyù:
Toång quaùtToång quaùt:: P(AP(A11AA22 . . . A. . . Ann) =) = P(AP(A11)P(A)P(A22 /A/A11). . .). . . P(AP(Ann/A/A11AA22. . . A. . . An-1n-1)) Neáu ANeáu A11, A, A22, . . . A, . . . Ann laølaø caùc b/c baát kyø, thì:caùc b/c baát kyø, thì:
(xem thí duï trang 36)(xem thí duï trang 36)
Neáu A, B laø hai b/coáNeáu A, B laø hai b/coá ñoäc laäp, thì:ñoäc laäp, thì: Heä quaû:Heä quaû: P(AB) =P(AB) = P(A)P(B)P(A)P(B)
P(AP(A11AA22 . . .. . . AAnn)=P(A)=P(A11)P(A)P(A22)). . .. . . P(AP(Ann)) Toång quaùtToång quaùt:: NeáuNeáu AA11,, AA22 , . . . , A, . . . , Ann laø caùc b/c ñoäc laäplaø caùc b/c ñoäc laäp toaøn phaàn, thì:toaøn phaàn, thì:
Chia ngaãu nhieân 9 hoäp söõa (trong ñoù coù 3 hoäp keùm phaåm chaát) thaønh 3 phaàn, moãi phaàn 3 hoäp. Tính xaùc suaát Thí duïThí duï::
GiaûiGiaûi:: Goïi AGoïi Aii (i = 1, 2) laø(i = 1, 2) laø bieán coá phaàn thöù i coùbieán coá phaàn thöù i coù 1 hoäp söõa keùm phaåm1 hoäp söõa keùm phaåm chaát.chaát.A laø bieán coá moãiA laø bieán coá moãi phaàn coù 1 hoäp keùmphaàn coù 1 hoäp keùm phaåm chaát.phaåm chaát. (A2 phuï thuoäc A1 ). AÙp duïng coâng thöùc nhaân A = AA = A11AA22
P(A) = P(AP(A) = P(A11)P(A)P(A22/A/A11)) 28 9 C C.C . C C.C 3 6 2 4 1 2 3 9 2 6 1 3 ==
3- Coâng thöùc xaùc suaát3- Coâng thöùc xaùc suaát ñaày ñuûñaày ñuû • Cho khoâng gian maãu SCho khoâng gian maãu S vaø Avaø A11, A, A22, . . . , A, . . . , Ann , B laø, B laø caùc bieán coá.caùc bieán coá. • Caùc bieán coá ACaùc bieán coá A11,, AA22, . . . , A, . . . , Ann laø heä bieánlaø heä bieán coá ñaày ñuû neáu chuùngcoá ñaày ñuû neáu chuùng thoûa maõn 2 ñieàu kieänthoûa maõn 2 ñieàu kieän
(1) A1 ∪ A2 . . . ∪ An = Ω (2) Ai ∩ Aj = ∅ (∀i ≠ j) i, j ∈{1, 2, . . . , n}• Khi ñoù ta coù:Khi ñoù ta coù:
P(B) =P(B) = (A(Aii)P(B/A)P(B/Aii)) ∑= n 1i P Caùc xaùc suaát P(ACaùc xaùc suaát P(A11);); P(AP(A22); . . . , P(A); . . . , P(Ann) thöôøng) thöôøng ñöôïc goïi laø caùc xaùcñöôïc goïi laø caùc xaùc suaát tieân nghieäm vaøsuaát tieân nghieäm vaø coâng thöùc treân ñöôïccoâng thöùc treân ñöôïc goïi laøgoïi laø coâng thöùc xaùccoâng thöùc xaùc
Thí duïThí duï:: Coù 3 kieänCoù 3 kieän haøng. Moãi kieän coù 5haøng. Moãi kieän coù 5 saûn phaåm, soá saûnsaûn phaåm, soá saûn phaåm loaïi A coù trongphaåm loaïi A coù trong kieän 1, kieän 2, kieän 3kieän 1, kieän 2, kieän 3 töông öùng laø: 4, 3, 2.töông öùng laø: 4, 3, 2. Choïn ngaãu nhieân moätChoïn ngaãu nhieân moät kieän roài töø kieän ñaõkieän roài töø kieän ñaõ choïn laáy ngaãu nhieân rachoïn laáy ngaãu nhieân ra
Giaûi:Giaûi: Goïi B laø bieán coá laáyGoïi B laø bieán coá laáy ñöôïc saûn phaåm loaïi A.ñöôïc saûn phaåm loaïi A. AA11, A, A22, A, A33 töông öùng laøtöông öùng laø caùc bieán coá choïn ñöôïccaùc bieán coá choïn ñöôïc kieän 1, 2, 3.kieän 1, 2, 3. AA11, A, A22, A, A33 laø moät heä bieánlaø moät heä bieán coá ñaày ñuû.coá ñaày ñuû.
KieänKieän 11 KieänKieän 22 KieänKieän 33              
ΩΩ AA11 AA22 AA33               BB
3 1 )A(P)A(P)A(P 321 === ∑= = 3 1i ii )A/B(P)A(P)B(P P(B/AP(B/A11) = = 0,8) = = 0,844 55 P(B/AP(B/A22) = =) = = 0,60,6 55 33 P(B/AP(B/A33) = =) = = 55 22
P(B) = (0,8 + 0,6 + 0,4)P(B) = (0,8 + 0,6 + 0,4) = 0,6= 0,6 11 33
4- Coâng thöùc Bayes4- Coâng thöùc Bayes Vôùi caùc giaû thieát nhöVôùi caùc giaû thieát nhö phaàn coâng thöùc xaùcphaàn coâng thöùc xaùc suaát ñaày ñuû vaø tasuaát ñaày ñuû vaø ta theâm ñieàu kieän laøtheâm ñieàu kieän laø pheùp thöû ñöôïc thöïcpheùp thöû ñöôïc thöïc hieän vaø bieán coá B ñaõhieän vaø bieán coá B ñaõ xaûy ra. Khi ñoù:xaûy ra. Khi ñoù:
P(AP(Aii/B) =/B) = ( i = 1, 2, .( i = 1, 2, . . . , n). . , n) )B(P )A/B(P)A(P ii
Caùc xaùc suaát P(ACaùc xaùc suaát P(Aii/B)/B) ñöôïc xaùc ñònh sau khiñöôïc xaùc ñònh sau khi ñaõ bieát keát quaû cuûañaõ bieát keát quaû cuûa pheùp thöû laø B ñaõ xaûypheùp thöû laø B ñaõ xaûy ra neân thöôøng ñöôïc goïira neân thöôøng ñöôïc goïi laø caùclaø caùc xaùc suaát haäuxaùc suaát haäu nghieämnghieäm.. Coâng thöùc Bayes xaùcCoâng thöùc Bayes xaùc ñònh laïi caùcñònh laïi caùc xaùc suaátxaùc suaát tieân nghieämtieân nghieäm P(AP(Aii)) khikhi
Thí duïThí duï:: Coù 3 kieänCoù 3 kieän haøng. Moãi kieän coù 5haøng. Moãi kieän coù 5 saûn phaåm, soá saûnsaûn phaåm, soá saûn phaåm loaïi A coù trongphaåm loaïi A coù trong kieän 1, kieän 2, kieän 3kieän 1, kieän 2, kieän 3 töông öùng laø: 4, 3, 2.töông öùng laø: 4, 3, 2. Choïn ngaãu nhieân moätChoïn ngaãu nhieân moät kieän roài töø kieän ñaõkieän roài töø kieän ñaõ choïn laáy ngaãu nhieân rachoïn laáy ngaãu nhieân ra
Giaûi:Giaûi: Goïi B laø bieán coá laáyGoïi B laø bieán coá laáy ñöôïc saûn phaåm loaïi A.ñöôïc saûn phaåm loaïi A. AA11, A, A22, A, A33 töông öùng laøtöông öùng laø caùc bieán coá choïn ñöôïccaùc bieán coá choïn ñöôïc kieän 1, 2, 3.kieän 1, 2, 3. AA11, A, A22, A, A33 laø moät heä bieánlaø moät heä bieán coá ñaày ñuû.coá ñaày ñuû.
Vì bieán coá B ñaõ xaûy ra, aùp duïng coâng thöùc Bayes ta coù: P(AP(A33/B) =/B) = == 11 33 0,40,4 0,60,6 99 22
TOÙM TAÉT CHÖÔNG 1TOÙM TAÉT CHÖÔNG 1 PheùpPheùp thöûthöû BieánBieán coácoá XaùcXaùc suaátsuaát cuûacuûa bieánbieán coácoá •• ÑN coå ñieånÑN coå ñieån •• ÑN thoángÑN thoáng keâkeâ •• Caùc coângCaùc coâng thöùcthöùc cô baûncô baûn •• Caùc loaïi b/cCaùc loaïi b/c •• Moái quan heäMoái quan heä Ñieàu kieänÑieàu kieän aùp duïngaùp duïng
Baøi taäp chuông 1Baøi taäp chuông 1 1.10; 1.15;1.10; 1.15; 1.16;1.16; 1.35; 1.36;1.35; 1.36; 1.39;1.39; 1.43; 1.48;1.43; 1.48; 1.49;1.49;
Heát chuông 1Heát chuông 1

More Related Content

PDF
Cndd dieuduongcb2 w
byLe Khac Thien Luan
 
PDF
Luận văn: Nghiên cứu khảo sát hệ thống điều khiển mức nước trong bao hơi của ...
byViết thuê trọn gói ZALO 0934573149
 
PDF
Luận văn: Khảo sát tôpô trên không gian các hàm chỉnh hình
byViết thuê trọn gói ZALO 0934573149
 
DOCX
Quan tri hoc cb 2014 new (1)
bydyby
 
PPT
Bai 22 dan nhiet thi gvg
byHanh Phuc la Toi
 
PDF
Ckc12
bytuanthuasac
 
DOC
Pm519 standart
byuserjigmee
 
PDF
"Thu Vien Sach Co Khi" – Cac phan tu trong he thong dieu khien khi nen
byThu Vien Co Khi
 
Cndd dieuduongcb2 w
byLe Khac Thien Luan
 
Luận văn: Nghiên cứu khảo sát hệ thống điều khiển mức nước trong bao hơi của ...
byViết thuê trọn gói ZALO 0934573149
 
Luận văn: Khảo sát tôpô trên không gian các hàm chỉnh hình
byViết thuê trọn gói ZALO 0934573149
 
Quan tri hoc cb 2014 new (1)
bydyby
 
Bai 22 dan nhiet thi gvg
byHanh Phuc la Toi
 
Ckc12
bytuanthuasac
 
Pm519 standart
byuserjigmee
 
"Thu Vien Sach Co Khi" – Cac phan tu trong he thong dieu khien khi nen
byThu Vien Co Khi
 

What's hot

PPT
Tudaicongphu va 3 s
byCuong Nguyen
 
PDF
Tom tat dien 2012
byqdai2008
 
PDF
Giáo trình Máy Xây Dựng - Nguyễn Phước Bình - ĐHBK Đà Nẵng
byshare-connect Blog
 
PDF
Thiết kế ctb trọng lực bêtong
bytrunganh94
 
PDF
Bai giang CTB cố định 1
byAnh Anh
 
PDF
Hướng dẫn Đồ Án Nền Móng
byshare-connect Blog
 
PPT
Bai 50 he sinh thai
byThao Nguyen
 
PDF
Gt am nhac_co_so_8709
byThiên Đường Tình Yêu
 
PDF
Gt am nhac_co_so_8709
byNguyễn Nhân Tín
 
PPT
Bai 21 Dac Diem Chung Cua Nganh Than Mem
bytrungtinh
 
DOC
Mot so bai tap xac suat thong ke
byMrNgo Ngo
 
PDF
Hoccokhi.vn Đồ Giá Cơ Khí - Nhiều Tác Giả, 194 Trang
byHọc Cơ Khí
 
PPT
Chuong 1-ktdc
byTin học Sức sống
 
PDF
Chức năng và phương pháp hành chính nhà nước
byjackjohn45
 
PDF
Cac lenh matlab_trong_dieu_khien_tu_dong_pham_quang_huy
bytamxuan2213
 
PDF
Luận án: Đặc điểm nông sinh học của một số giống bưởi, HAY
byDịch vụ viết bài trọn gói ZALO 0917193864
 
PDF
Dieu khien thuy_luc_va_khi_nen_6898
byCửa Hàng Vật Tư
 
PDF
Bao cao de_tai_proii
byvinhdvan
 
DOCX
Soril5
bynyamtaivan
 
Tudaicongphu va 3 s
byCuong Nguyen
 
Tom tat dien 2012
byqdai2008
 
Giáo trình Máy Xây Dựng - Nguyễn Phước Bình - ĐHBK Đà Nẵng
byshare-connect Blog
 
Thiết kế ctb trọng lực bêtong
bytrunganh94
 
Bai giang CTB cố định 1
byAnh Anh
 
Hướng dẫn Đồ Án Nền Móng
byshare-connect Blog
 
Bai 50 he sinh thai
byThao Nguyen
 
Gt am nhac_co_so_8709
byThiên Đường Tình Yêu
 
Gt am nhac_co_so_8709
byNguyễn Nhân Tín
 
Bai 21 Dac Diem Chung Cua Nganh Than Mem
bytrungtinh
 
Mot so bai tap xac suat thong ke
byMrNgo Ngo
 
Hoccokhi.vn Đồ Giá Cơ Khí - Nhiều Tác Giả, 194 Trang
byHọc Cơ Khí
 
Chuong 1-ktdc
byTin học Sức sống
 
Chức năng và phương pháp hành chính nhà nước
byjackjohn45
 
Cac lenh matlab_trong_dieu_khien_tu_dong_pham_quang_huy
bytamxuan2213
 
Luận án: Đặc điểm nông sinh học của một số giống bưởi, HAY
byDịch vụ viết bài trọn gói ZALO 0917193864
 
Dieu khien thuy_luc_va_khi_nen_6898
byCửa Hàng Vật Tư
 
Bao cao de_tai_proii
byvinhdvan
 
Soril5
bynyamtaivan
 

Similar to Chg1 xs k38

PDF
Giai tich 1
byInformatics and Maths
 
PDF
Giai tich 1
byVcoi Vit
 
PDF
Mật thư - DoiSongTrai.NET
byTibi Nguyễn
 
PDF
Bai tap vat ly a3
byvuongthanhtimeo
 
PDF
Phương pháp số và lập trình - Tính sai số
byHajunior9x
 
PDF
Cơ học lý thuyết.
bywww. mientayvn.com
 
PDF
Kỹ thuật điện - Nguyễn Kim Đính - BK HCM
byTien Anh Nguyen Van
 
PDF
MAY-DIEN-1
byMan_Ebook
 
PDF
Decuong cn8 01 11
byHọc Tập Long An
 
PDF
Decuong cn8 01 11
byHọc Tập Long An
 
PDF
Decuong cn8 01 11
byHọc Tập Long An
 
PPT
Chu De 3 Le Quy Don
bynhxp2001
 
PDF
Chuong 1 khai niem ve nen mong
byHoàng Gia
 
PDF
Chuong2 tohop xacsuat
bynguyen khiem
 
PDF
Ly thuyet vat ly full
byAdagio Huynh
 
PDF
giao-trinh-co-hoc-ly-thuyet-vu-duy-cuong.pdf
byNghiatran Cong
 
PDF
Giao trinh do-dien-dientu
byNguyễn Nho Vĩnh
 
PDF
Hd thuctap quanday bai 1
byHoàng Đức
 
DOC
may cat kim loai Chuong viiia
byNguyễn Hải Sứ
 
PDF
Ct vat ly nc
byHương Thảo Hồ
 
Giai tich 1
byInformatics and Maths
 
Giai tich 1
byVcoi Vit
 
Mật thư - DoiSongTrai.NET
byTibi Nguyễn
 
Bai tap vat ly a3
byvuongthanhtimeo
 
Phương pháp số và lập trình - Tính sai số
byHajunior9x
 
Cơ học lý thuyết.
bywww. mientayvn.com
 
Kỹ thuật điện - Nguyễn Kim Đính - BK HCM
byTien Anh Nguyen Van
 
MAY-DIEN-1
byMan_Ebook
 
Decuong cn8 01 11
byHọc Tập Long An
 
Decuong cn8 01 11
byHọc Tập Long An
 
Decuong cn8 01 11
byHọc Tập Long An
 
Chu De 3 Le Quy Don
bynhxp2001
 
Chuong 1 khai niem ve nen mong
byHoàng Gia
 
Chuong2 tohop xacsuat
bynguyen khiem
 
Ly thuyet vat ly full
byAdagio Huynh
 
giao-trinh-co-hoc-ly-thuyet-vu-duy-cuong.pdf
byNghiatran Cong
 
Giao trinh do-dien-dientu
byNguyễn Nho Vĩnh
 
Hd thuctap quanday bai 1
byHoàng Đức
 
may cat kim loai Chuong viiia
byNguyễn Hải Sứ
 
Ct vat ly nc
byHương Thảo Hồ
 

Chg1 xs k38

  • 1.
    GVGV HOAØNG NGOÏCHOAØNG NGOÏC NHAÄMNHAÄM Boämoân:Boä moân: TOAÙNTOAÙN KINH TEÁKINH TEÁ Khoa:Khoa: TOAÙN -TOAÙN - THOÁNG KEÂTHOÁNG KEÂ
  • 2.
    Phaàn IPhaàn I LYÙTHUYEÁT XAÙCLYÙ THUYEÁT XAÙC SUAÁTSUAÁT
  • 3.
    Chöông 1Chöông 1 Xaùcsuaát cuûa bieánXaùc suaát cuûa bieán coácoá vaø caùc coâng thöùc tínhvaø caùc coâng thöùc tính xaùc suaátxaùc suaátChöông 2Chöông 2 Ñaïi löôïng ngaãu nhieânÑaïi löôïng ngaãu nhieân vaø phaân phoái xaùcvaø phaân phoái xaùc suaátsuaát
  • 4.
    Chöông 3Chöông 3 Moätsoá phaân phoáiMoät soá phaân phoái xaùc suaát thoâng duïngxaùc suaát thoâng duïng Chöông 4Chöông 4 Ñaïi löôïng ngaãu nhieânÑaïi löôïng ngaãu nhieân hai chieàu – haøm cuûahai chieàu – haøm cuûa caùc ñaïi löôïngcaùc ñaïi löôïng
  • 5.
    Chöông 6Chöông 6 Maãungaãu nhieânMaãu ngaãu nhieân Phaàn IIPhaàn II THOÁNG KEÂTHOÁNG KEÂ TOAÙNTOAÙN Chöông 5Chöông 5 Luaät soá lôùnLuaät soá lôùn vaø caùc ñònh lyù giôùivaø caùc ñònh lyù giôùi haïnhaïn
  • 6.
    Chöông 8Chöông 8 Kieåmñònh giaû thieátKieåm ñònh giaû thieát thoáng keâthoáng keâ Chöông 7Chöông 7 Öôùc löôïng caùc tham soáÖôùc löôïng caùc tham soá ñaëcñaëc tröng cuûa ñaïi löôïngtröng cuûa ñaïi löôïng ngaãu nhieânngaãu nhieân
  • 7.
    1-1- Lyù thuyeátxaùc suaátLyù thuyeát xaùc suaát & thoáng keâ toaùn.& thoáng keâ toaùn. Hoaøng NgoïcHoaøng Ngoïc NhaämNhaäm NXB Kinh t TP H Chíế ồNXB Kinh t TP H Chíế ồ TAØI LIEÄU HOÏC TAÄPTAØI LIEÄU HOÏC TAÄP VAØ THAM KHAÛOVAØ THAM KHAÛO
  • 9.
    3-3- Baøi taäpxaùc suaátBaøi taäp xaùc suaát thoáng keâthoáng keâ Th s Hoaøng NgoïcTh s Hoaøng Ngoïc Nhaäm,Nhaäm, 2-2- Giaùo trình lyù thuyeátGiaùo trình lyù thuyeát xaùc suaát & thoáng keâxaùc suaát & thoáng keâ toaùn hoïctoaùn hoïc Ths Traàn Gia TuøngThs Traàn Gia Tuøng NXB ÑH Quoác gia TP Hoà ChíNXB ÑH Quoác gia TP Hoà Chí Minh, 2009Minh, 2009
  • 11.
    Cách đánh giá:Cáchđánh giá: - Điểm quá trình: 30%;- Điểm quá trình: 30%; - Điểm thi kết thúc HP: 70%- Điểm thi kết thúc HP: 70% - Điểm quá trình bao gồm:- Điểm quá trình bao gồm: điểm kiểm tra giữa kỳ,điểm kiểm tra giữa kỳ, điểm thảo thuận, sửa bài tậpđiểm thảo thuận, sửa bài tập trên lớptrên lớp, . . .. . .
  • 12.
    Bài kiểm tragiữa kỳ: Thời gian: 45 phút. Nội dung: phần xác suất. Bài thi kết thúc học phần: Thôøi gian 75 Phuùt. Coù hai phaàn: Phaàn I: traéc nghieäm Phaàn II: tự luận
  • 13.
    PHAÀN I Chöông 1Chöông1 LYÙ THUYEÁT XAÙCLYÙ THUYEÁT XAÙC SUAÁTSUAÁT XAÙC SUAÁT CUÛA BIEÁNXAÙC SUAÁT CUÛA BIEÁN COÁ VAØ CAÙCCOÁ VAØ CAÙC COÂNG THÖÙC TÍNH XAÙCCOÂNG THÖÙC TÍNH XAÙC SUAÁTSUAÁTI- Pheùp thöû, bieán coá,I- Pheùp thöû, bieán coá, khoâng giankhoâng gian
  • 14.
    Caùc thí duCaùcthí duï:ï:  Tung (gieo) moät ñoàngTung (gieo) moät ñoàng xu.xu.  Tung (gieo) moät conTung (gieo) moät con suùc saéc.suùc saéc.  Choïn ngaãu nhieân 2Choïn ngaãu nhieân 2 saûn phaåm töø kieänsaûn phaåm töø kieän haøng coù 5 saûn phaåmhaøng coù 5 saûn phaåm ñeå kieåm tra.ñeå kieåm tra.
  • 15.
     Quan saùtñieåm thiQuan saùt ñieåm thi moân toaùn cao caáp cuûamoân toaùn cao caáp cuûa moät sinh vieân heä CQ.moät sinh vieân heä CQ.  Laøm caùc thí nghieämLaøm caùc thí nghieäm ñeå nghieân cöùu veàñeå nghieân cöùu veà naêng suaát cuûa moätnaêng suaát cuûa moät gioáng luùa môùi.gioáng luùa môùi.
  • 16.
    •• Pheùp thöûlaø moät thí nghieäm hay quan saùt. •• Pheùp thöû laø nhöõng coâng vieäc, nhöõng haønh ñoäng cuûa con ngöôøi nhaèm quan saùt, nghieân cöùu moät hieän töôïng, moät ñoái töôïng
  • 17.
    Khi thöïc hieänmoät pheùp thöû coù nhieàu keát quaû coù theå xaûy ra. Coù keát quaû ñôn giaûn, coù keát quaû phöùc hôïp.
  • 18.
    Khi tung moätcon suùcKhi tung moät con suùc saéc, suùc saéc ra maëtsaéc, suùc saéc ra maët 1 chaám, 2 chaám, . . . ,1 chaám, 2 chaám, . . . , 6 chaám laø nhöõng6 chaám laø nhöõng keát quaû ñôn giaûn,keát quaû ñôn giaûn, suùc saéc ra maëtsuùc saéc ra maët chaün, suùc saéc rachaün, suùc saéc ra
  • 19.
    Keát quaû ñôngiaûnKeát quaû ñôn giaûn nhaát ñöôïc goïi laønhaát ñöôïc goïi laø bieán coá sô caápbieán coá sô caáp Taäp hôïp taát caû caùcTaäp hôïp taát caû caùc bieán coá sô caáp ñöôïcbieán coá sô caáp ñöôïc goïi laøgoïi laø khoâng giankhoâng gian caùc bieán coá sôcaùc bieán coá sô caápcaáp (khoâng gian(khoâng gian
  • 20.
    •• Moãi taäpcon cuûaMoãi taäp con cuûa khoâng gian maãu ñöôïckhoâng gian maãu ñöôïc goïi laøgoïi laø bieán coábieán coá..•• Bieán coá laø moätBieán coá laø moät keát quaû coù theå xaûykeát quaû coù theå xaûy ra khi thöïc hieänra khi thöïc hieän pheùp thöû.pheùp thöû.•• Khoâng gian caùcKhoâng gian caùc bieán coá sô caáp kyùbieán coá sô caáp kyù
  • 21.
    Gieo moät consuùc saécGieo moät con suùc saéc ωi (i = 1, 2, . . . , 6) chæ(i = 1, 2, . . . , 6) chæ keát quaû suùc saéc xuaátkeát quaû suùc saéc xuaát hieän maët i chaám.hieän maët i chaám. Thí duï 1:   Ω = {ω1 , ω2 , ω3 , ω4 , ω5 , ω6 }
  • 22.
    Thí duï 2:Kieåm tra 1Kieåm tra 1 saûn phaåm choïn ngaãusaûn phaåm choïn ngaãu nhieân töø moät kieännhieân töø moät kieän haøng. Giaû thieát saûnhaøng. Giaû thieát saûn phaåm hoaëc loaïi I,phaåm hoaëc loaïi I, hoaëc loaïi II, hoaëchoaëc loaïi II, hoaëc pheá phaåm.pheá phaåm.   Ω = {ω1 , ω2 , ω3 }
  • 23.
    Thí duï 3:Kieåm tra 2Kieåm tra 2 saûn phaåm choïn ngaãusaûn phaåm choïn ngaãu nhieân töø moät kieännhieân töø moät kieän haøng. Giaû thieát saûnhaøng. Giaû thieát saûn phaåm hoaëc loaïi I,phaåm hoaëc loaïi I, hoaëc loaïi II, hoaëchoaëc loaïi II, hoaëc pheá phaåm.pheá phaåm. Khoâng gian caùc bieán coá sôKhoâng gian caùc bieán coá sô caáp goàm coù caùc phaàn töûcaáp goàm coù caùc phaàn töû naøo ?naøo ?
  • 24.
    spsp11 spsp22 LoaïiLoaïi II LoaïiLoaïiIIII LoaïiLoaïi PPPP LoaïiLoaïi II LoaïiLoaïi IIII LoaïiLoaïi PPPP            Ω = {ω1 , ω2 , . . . , ω }
  • 25.
    Chuù yù: Caùc bieáncoá cuï theåCaùc bieán coá cuï theå luoân gaén lieàn vôùiluoân gaén lieàn vôùi pheùp thöû cuï theå.pheùp thöû cuï theå. PhePhe ùpùp KhoâKhoâ ngng giangian caùccaùc BieáBieá nn
  • 26.
    Pheùp thöûPheùp thöûKh.gian maãuKh. gian maãu Bieán coáBieán coá Tung 1Tung 1 ñoàng xuñoàng xu ΩΩ = {H, C}= {H, C} XHXH maët hình (H)maët hình (H) XHXH maët chöõ (C)maët chöõ (C). Tung 1Tung 1 concon suùcsuùc saécsaéc Ω = {= {ωω11,, ωω22,, . . . ,. . . , ωω66}} XH maët 3, 6,XH maët 3, 6, XH maët chaün,XH maët chaün, . . .. . . Kieåm traKieåm tra 1 saûn1 saûn phaåmphaåm Ω == {{ωω11,, ωω22,, ωω33}} SP laø loaïi I,SP laø loaïi I, SP laø loaïi II,SP laø loaïi II, SP laø pheá phaåmSP laø pheá phaåm
  • 27.
     Bieán coángaãuBieán coá ngaãu nhieânnhieân A, B, C, D, E,A, B, C, D, E, F, . . .F, . . .  Bieán coá chaécBieán coá chaéc chaén (chaén (Ω)  Bieán coá khoângBieán coá khoâng theå (theå (∅))
  • 28.
    ÑònhÑònh nghóa 1nghóa 1:: Bieáncoá A ñöôïc goïi laøBieán coá A ñöôïc goïi laø keùo theo bieán coá B,keùo theo bieán coá B, kyù hieäu laøkyù hieäu laø AA ⊂⊂ BB neáuneáu A xaûy ra thì B cuõngA xaûy ra thì B cuõng xaûy ra.xaûy ra. II- MOÁI QUAN HEÄ GIÖÕA CAÙCII- MOÁI QUAN HEÄ GIÖÕA CAÙC BIEÁN COÁBIEÁN COÁ
  • 29.
    Thí duïThí duï:: Tungmoät con suùcTung moät con suùc saéc, goïi A laø bieánsaéc, goïi A laø bieán coá “suùc saéc ra maëtcoá “suùc saéc ra maët 2” vaø B laø bieán coá2” vaø B laø bieán coá “suùc saéc ra maët“suùc saéc ra maët chaün” thì:chaün” thì:
  • 30.
    ÑònhÑònh nghóa 2nghóa 2:: Bieáncoá A vaø B ñöôïcBieán coá A vaø B ñöôïc goïi laø haigoïi laø hai bieán coábieán coá töông ñöôngtöông ñöông,, kyù hieäukyù hieäu laølaø A = BA = B neáu Aneáu A ⊂⊂ BB vaø Bvaø B ⊂⊂ A.A.Neáu A = B thì: P(A) =Neáu A = B thì: P(A) = P(B)P(B)
  • 31.
    Thí duïThí duï:: Kieåmtra 2 saûnKieåm tra 2 saûn phaåm. Goïi A laøphaåm. Goïi A laø bieán coá “coù ít nhaátbieán coá “coù ít nhaát moät pheá phaåm” vaømoät pheá phaåm” vaø B laø bieán coá “coù 1B laø bieán coá “coù 1 pheá phaåm hoaëc coùpheá phaåm hoaëc coù
  • 32.
    CaâuCaâu hoûihoûi::Taïi sao xaùcsuaátTaïi sao xaùc suaát cuûa caùc bieán coácuûa caùc bieán coá töông ñöông laïi baèngtöông ñöông laïi baèng nhau ?nhau ?
  • 33.
    Toång cuûa 2bieán coá AToång cuûa 2 bieán coá A vaø B laø moät bieán coá,vaø B laø moät bieán coá, kyù hieäu laøkyù hieäu laø AA ∪∪ BB (hoaëc(hoaëc A + BA + B). Bieán coá naøy). Bieán coá naøy xaûy ra khi vaø chæ khixaûy ra khi vaø chæ khi coù ít nhaát moät trong haicoù ít nhaát moät trong hai bieán coá A, B xaûy ra.bieán coá A, B xaûy ra. ÑònhÑònh nghóa 3nghóa 3::
  • 34.
    Thí duïThí duï:: Quansaùt 2 xaï thuû cuøngQuan saùt 2 xaï thuû cuøng baén vaøo moät bia. Moãibaén vaøo moät bia. Moãi xaï thuû baén moät vieân.xaï thuû baén moät vieân. Goïi A laø bieán coá “Goïi A laø bieán coá “xaïxaï thuû thöù nhaát baénthuû thöù nhaát baén truùng biatruùng bia”, B laø bieán”, B laø bieán coá “coá “xaï thuû thöù haixaï thuû thöù hai
  • 35.
    Ñònh nghóaÑònh nghóa 44:: Tíchcuûa hai bieán coá ATích cuûa hai bieán coá A vaø B laø moät bieán coá,vaø B laø moät bieán coá, kkyù hieäu laø Ayù hieäu laø A ∩∩ BB ((hoaëc AB), bieán coáhoaëc AB), bieán coá naøy xaûy ra khi vaø chænaøy xaûy ra khi vaø chæ khi caû A vaø B xaûy ra.khi caû A vaø B xaûy ra.
  • 36.
    Thí duïThí duï:: Xeùtpheùp thöû quan saùtXeùt pheùp thöû quan saùt hai xaï thuû cuøng baén vaøohai xaï thuû cuøng baén vaøo moät bia (moãi ngöôøi baénmoät bia (moãi ngöôøi baén moät vieân). Goïi A laø bieánmoät vieân). Goïi A laø bieán coá “coá “xaï thuû thöù nhaátxaï thuû thöù nhaát baén traätbaén traät”, B laø bieán coá”, B laø bieán coá ““xaï thuû thöù hai baénxaï thuû thöù hai baén traättraät” vaø C laø bieán coá “” vaø C laø bieán coá “
  • 37.
    Ñònh nghóaÑònh nghóa 55:: Haibieán coá A vaø BHai bieán coá A vaø B ñöôïc goïi laø xungñöôïc goïi laø xung khaéc neáu Akhaéc neáu A∩∩B =B = ∅∅.. A, B laø 2 bieán coáA, B laø 2 bieán coá xung khaéc neáu chuùngxung khaéc neáu chuùng khoâng theå ñoàngkhoâng theå ñoàng thôøi xaûy ra khi thöïcthôøi xaûy ra khi thöïc
  • 38.
    Chuù yùïChuù yùï:: A,B laø 2 bieán coáA, B laø 2 bieán coá khoâng xung khaéckhoâng xung khaéc neáu chuùng coù theåneáu chuùng coù theå ñoàng thôøi xaûy ra khiñoàng thôøi xaûy ra khi thöïc hieän pheùpthöïc hieän pheùp thöûù.thöûù.
  • 39.
    Thí duï 1Thíduï 1:: Kieåm tra 2 saûnKieåm tra 2 saûn phaåm. Goïi A laøphaåm. Goïi A laø bieán coá “coù 1 pheábieán coá “coù 1 pheá phaåm”. B laø bieánphaåm”. B laø bieán coá “khoâng coù pheácoá “khoâng coù pheá phaåm” thì A, B laø 2phaåm” thì A, B laø 2
  • 40.
    Thí duï 2Thíduï 2:: Kieåm tra 3 saûnKieåm tra 3 saûn phaåm. Goïi A laøphaåm. Goïi A laø bieán coá “saûn phaåmbieán coá “saûn phaåm thöù nhaát laø saûnthöù nhaát laø saûn phaåm toát; B laø bieánphaåm toát; B laø bieán coá saûn phaåm thöùcoá saûn phaåm thöù
  • 41.
    Ñònh nghóaÑònh nghóa 66:: Bieáncoá ñoái laäpBieán coá ñoái laäp vôùi bieán coá A, kyùvôùi bieán coá A, kyù hieäu laø A, neáu A, Ahieäu laø A, neáu A, A xung khaéc vaø Axung khaéc vaø A∪∪A =A = ΩΩ.. Bieán coá “ khoângBieán coá “ khoâng xaûy ra bieán coá A”xaûy ra bieán coá A” ñöôïc goïi laø bieán coáñöôïc goïi laø bieán coá
  • 42.
    Thí duïThí duï:: Kieåmtra 5 saûnKieåm tra 5 saûn phaåm. Goïi A laøphaåm. Goïi A laø bieán coá “coù ít nhaátbieán coá “coù ít nhaát 3 saûn phaåm toát”. A3 saûn phaåm toát”. A laø bieán coá “soálaø bieán coá “soá saûn phaåm toátsaûn phaåm toát
  • 43.
    Bieåu ñoàBieåu ñoà VENNVENN:: Quansaùt 2 xaï thuû cuøngQuan saùt 2 xaï thuû cuøng baén vaøo moät bia. Moãibaén vaøo moät bia. Moãi xaï thuû baén moät vieân.xaï thuû baén moät vieân. Goïi A laø bieán coá “Goïi A laø bieán coá “xaïxaï thuû thöù nhaát baénthuû thöù nhaát baén truùng biatruùng bia”, B laø bieán”, B laø bieán coá “coá “xaï thuû thöù haixaï thuû thöù hai baén truùng biabaén truùng bia”, C laø”, C laø
  • 44.
  • 45.
    Quan saùt 2xaï thuû cuøngQuan saùt 2 xaï thuû cuøng baén vaøo moät bia. Moãibaén vaøo moät bia. Moãi xaï thuû baén moät vieân.xaï thuû baén moät vieân. Goïi A laø bieán coá “Goïi A laø bieán coá “xaïxaï thuû thöù nhaát baénthuû thöù nhaát baén traättraät”, B laø bieán coá “”, B laø bieán coá “xaïxaï thuû thöù hai baén traätthuû thöù hai baén traät”,”, C laø bieán coá “C laø bieán coá “bia khoângbia khoâng truùng ñaïntruùng ñaïn”.”.
  • 46.
  • 47.
    Quan saùt 2xaï thuû cuøngQuan saùt 2 xaï thuû cuøng baén vaøo moät bia. Moãibaén vaøo moät bia. Moãi xaï thuû baén moät vieân.xaï thuû baén moät vieân. Goïi A laø bieán coá “Goïi A laø bieán coá “coùcoù moät vieân truùngmoät vieân truùng”, B laø”, B laø bieán coá “bieán coá “coù 2 vieâncoù 2 vieân truùngtruùng”, A, B xung khaéc”, A, B xung khaéc
  • 48.
  • 49.
    Quan saùt 2xaï thuû cuøngQuan saùt 2 xaï thuû cuøng baén vaøo moät bia. Moãibaén vaøo moät bia. Moãi xaï thuû baén moät vieân.xaï thuû baén moät vieân. Goïi A laø bieán coá “Goïi A laø bieán coá “coùcoù moät vieân truùngmoät vieân truùng”, thì A”, thì A seõ laø bieán coá “seõ laø bieán coá “coù 2coù 2 vieân truùng hoaëc khoângvieân truùng hoaëc khoâng coù vieân naøo truùngcoù vieân naøo truùng”.”.
  • 50.
  • 51.
  • 52.
    Caâu hoûi: Kieåm tra3 saûn phaåmKieåm tra 3 saûn phaåm choïn ngaãu nhieân töøchoïn ngaãu nhieân töø moät kieän haøng. Giaûmoät kieän haøng. Giaû thieát saûn phaåm hoaëcthieát saûn phaåm hoaëc laø ñaït tieâu chuaån hoaëclaø ñaït tieâu chuaån hoaëc khoâng ñaït tieâu chuaån.khoâng ñaït tieâu chuaån. -Khoâng gian maãu coù baoKhoâng gian maãu coù bao nhieâu phaàn töû ? Haõynhieâu phaàn töû ? Haõy
  • 53.
    Haõy chæ racaùc taäp hôïpHaõy chæ ra caùc taäp hôïp bieåu dieãn caùc b/c sau:bieåu dieãn caùc b/c sau: 1-1- Khoâng coù saûn phaåmKhoâng coù saûn phaåm ñaït tieâu chuaån trong 3 spñaït tieâu chuaån trong 3 sp kieåm tra.kieåm tra. 2-2- Coù 1 sp ñaït tieâu chuaånCoù 1 sp ñaït tieâu chuaån trong 3 sp kieåm tra.trong 3 sp kieåm tra. 3-3- Coù 2 sp ñaït tieâu chuaånCoù 2 sp ñaït tieâu chuaån trong 3 sp kieåm tra.trong 3 sp kieåm tra. 4-4- Caû 3 sp k.tra ñeàu ñaïtCaû 3 sp k.tra ñeàu ñaït
  • 54.
  • 55.
    Caùc tínhCaùc tính chaátchaát:: A ∪ B = BB = B ∪∪ AA  A ∩ B = BB = B ∩∩ AA  A∪(BB∪∪C) =C) = (A(A∪∪B)B)∪∪CC = A= A ∪∪ BB ∪∪ CC
  • 56.
     A∩(BB∩∩CC) =() = (AA∩∩BB))∩∩CC == AA ∩∩ BB ∩∩ CC A∪(BB∩∩CC)=)= ((AA∪∪BB))∩∩((AA∪∪CC)) A∩(BB∪∪CC)=)= ((AA∩∩BB))∪∪((AA∩∩CC))
  • 57.
  • 58.
    1- Khaùi nieämveà xaùc1- Khaùi nieäm veà xaùc suaát:suaát: Xaùc suaátXaùc suaát cuûa moätcuûa moät bieán coá laø moät con soábieán coá laø moät con soá bieåu thò khaû naêng xaûybieåu thò khaû naêng xaûy ra bieán coá ñoù khi thöïcra bieán coá ñoù khi thöïc
  • 59.
    Xeùt pheùp thöûXeùtpheùp thöû ττ, giaû söû, giaû söû khoâng gian maãu coù höõukhoâng gian maãu coù höõu haïn caùc bieán coá sô caáphaïn caùc bieán coá sô caáp vaø caùc bieán coá naøy coùvaø caùc bieán coá naøy coù khaû naêng xaûy ra nhökhaû naêng xaûy ra nhö nhau (ta goïi laø ñoàngnhau (ta goïi laø ñoàng khaû naêng).khaû naêng). 2- Ñònh nghóa coå ñieån2- Ñònh nghóa coå ñieån veà xaùc suaátveà xaùc suaát
  • 60.
    Ta noùi ñôngiaûn: n laø soáTa noùi ñôn giaûn: n laø soá tröôøng hôïp ñoàng khaûtröôøng hôïp ñoàng khaû naêng coù theå xaûy ra khinaêng coù theå xaûy ra khi thöïc hieän pheùp thöûthöïc hieän pheùp thöû ττ •• Bieán coá ABieán coá A == AA11∪∪AA22∪∪ .. .. .. ∪∪ AAmm trong ñoù Atrong ñoù Aii ( i = 1, 2, . . . ,( i = 1, 2, . . . , m) laø caùc bieán coá sôm) laø caùc bieán coá sô caáp.caáp. Ta noùi ñôn giaûn: m laø
  • 61.
    Khi ñoù, xaùcsuaátKhi ñoù, xaùc suaát cuûa bieán coá A, kyùcuûa bieán coá A, kyù hieäu laø P(A), ñöôïchieäu laø P(A), ñöôïc ñònh nghóañònh nghóa laø:laø: P(A)P(A) == mm nn
  • 62.
    Thí duïThí duï 11Tungmoät con suùcTung moät con suùc saéc caân ñoái vaøsaéc caân ñoái vaø ñoàng chaát.ñoàng chaát.Caùc tröôøng hôïpCaùc tröôøng hôïp ñoàng khaû naêng laø:ñoàng khaû naêng laø: suùc saéc ra maët 1,suùc saéc ra maët 1, suùc saéc ra maët 2, . . .suùc saéc ra maët 2, . . .
  • 63.
    Thí duïThí duï 22Choïnngaãu nhieânChoïn ngaãu nhieân moät sinh vieân töømoät sinh vieân töø moät lôùp coù 50 sinhmoät lôùp coù 50 sinh vieân (trong ñoù coù 30vieân (trong ñoù coù 30 nöõ vaø 20 nam).nöõ vaø 20 nam).
  • 64.
    Tröôøng hôïp ñoàngTröôønghôïp ñoàng khaû naêng laø nhöõngkhaû naêng laø nhöõng tröôøng hôïp naøo?tröôøng hôïp naøo? Bao nhieâu tröôøngBao nhieâu tröôøng hôïp ñoàng khaûhôïp ñoàng khaû naêng?naêng?
  • 65.
    Thí duïThí duï 33Choïnngaãu nhieân 2Choïn ngaãu nhieân 2 saûn phaåm töø moätsaûn phaåm töø moät kieän haøng coù 5 saûnkieän haøng coù 5 saûn phaåm (trong ñoù coù 3phaåm (trong ñoù coù 3 saûn phaåm loaïi I vaøsaûn phaåm loaïi I vaø 2 saûn phaåm loaïi II).2 saûn phaåm loaïi II).
  • 66.
    Tröôøng hôïp ñoàngTröôønghôïp ñoàng khaû naêng laø nhöõngkhaû naêng laø nhöõng tröôøng hôïp naøo?tröôøng hôïp naøo? Bao nhieâu tröôøngBao nhieâu tröôøng hôïp ñoàng khaûhôïp ñoàng khaû naêng?naêng?
  • 67.
  • 68.
    Thí duïThí duï 11Tungmoät con suùc saécTung moät con suùc saéc caân ñoái vaø ñoàng chaát.caân ñoái vaø ñoàng chaát. Goïi A laø b/c suùc saéc raGoïi A laø b/c suùc saéc ra maët chaünmaët chaünCaùc tröôøng hôïp thuaänCaùc tröôøng hôïp thuaän lôïi cho A laø: suùc saéc ralôïi cho A laø: suùc saéc ra maët 2, suùc saéc ra maëtmaët 2, suùc saéc ra maët 4, suùc saéc ra maët 6.4, suùc saéc ra maët 6.
  • 69.
    Thí duïThí duï 22Choïnngaãu nhieânChoïn ngaãu nhieân moät sinh vieân töømoät sinh vieân töø moät lôùp coù 50 sinhmoät lôùp coù 50 sinh vieân (trong ñoù coù 30vieân (trong ñoù coù 30 nöõ vaø 20 nam). Goïinöõ vaø 20 nam). Goïi B laø bieán coá choïnB laø bieán coá choïn
  • 70.
    Tröôøng hôïp thuaänTröôønghôïp thuaän lôïi cho B laø nhöõnglôïi cho B laø nhöõng tröôøng hôïp naøo?tröôøng hôïp naøo? Bao nhieâu tröôøngBao nhieâu tröôøng hôïp thuaän lôïi chohôïp thuaän lôïi cho bieán coá B?bieán coá B?
  • 71.
    Thí duïThí duï 33Choïnngaãu nhieân 2Choïn ngaãu nhieân 2 saûn phaåm töø moätsaûn phaåm töø moät kieän haøng coù 5 saûnkieän haøng coù 5 saûn phaåm (trong ñoù coù 3phaåm (trong ñoù coù 3 saûn phaåm loaïi I vaø 2saûn phaåm loaïi I vaø 2 saûn phaåm loaïi II). Goïisaûn phaåm loaïi II). Goïi C laø bieán coá choïn ñöôïcC laø bieán coá choïn ñöôïc
  • 72.
    Tröôøng hôïp thuaänTröôønghôïp thuaän lôïi cho C laø nhöõnglôïi cho C laø nhöõng tröôøng hôïp naøo?tröôøng hôïp naøo? Bao nhieâu tröôøngBao nhieâu tröôøng hôïphôïp thuaän lôïi cho bieánthuaän lôïi cho bieán coá C?coá C?
  • 73.
  • 74.
    b- Caùc tínhchaát cuûab- Caùc tính chaát cuûa xaùc suaát:xaùc suaát:  Neáu A laø b/coá ngaãuNeáu A laø b/coá ngaãu nhieân thì:nhieân thì: 0 < P(A) < 10 < P(A) < 1 NeáuNeáu ΩΩ laø b/coá chaéclaø b/coá chaéc chaén thì:chaén thì: P(P(ΩΩ) = 1) = 1 NeáuNeáu ∅∅ laø b/coá khoânglaø b/coá khoâng theå thì:theå thì: P(P(∅∅) = 0) = 0
  • 75.
    Vôùi A laøbieánVôùi A laø bieán coá baátcoá baát kyø, ta luoânkyø, ta luoân coù:coù: 00 ≤≤ P(A)P(A) ≤≤ 11
  • 76.
    3- Caùc khaùinieäm3- Caùc khaùi nieäm cuûa giaûi tích toå hôïpcuûa giaûi tích toå hôïp ** Qui taéc nhaân
  • 77.
    ThíThí duïduï:Coù hai hoäp,hoäp thöùCoù hai hoäp, hoäp thöù nhaát coù 3 saûn phaåm,nhaát coù 3 saûn phaåm, hoäp thöù hai coù 2 saûnhoäp thöù hai coù 2 saûn phaåm. Laáy ngaãu nhieânphaåm. Laáy ngaãu nhieân töø hoäp thöù nhaát ra 2töø hoäp thöù nhaát ra 2 saûn phaåm, töø hoäp thöùsaûn phaåm, töø hoäp thöù hai laáy ngaãu nhieân ra 1hai laáy ngaãu nhieân ra 1
  • 78.
            nn11= 3= 3   nn22=2= 2                 nn == 66
  • 79.
    21nnn = Neáu ñoáitöôïng A coù theåNeáu ñoái töôïng A coù theå ñöôïc choïn baèng nñöôïc choïn baèng n11 caùch,caùch, vôùi moãi caùch choïn A tavôùi moãi caùch choïn A ta coù ncoù n22 caùch choïn ñoái töôïngcaùch choïn ñoái töôïng B. Khi ñoù soá caùch choïn AB. Khi ñoù soá caùch choïn A vaø B laø:vaø B laø:
  • 80.
    Toång quaùt: NeáuchoïnNeáu choïn k ñoái töôïng thì soá caùchk ñoái töôïng thì soá caùch choïn k ñoái töôïng seõ laø:choïn k ñoái töôïng seõ laø: k21 n....nnn = (n(nii laø soá caùch choïn ñoáilaø soá caùch choïn ñoái töôïng thöù i )töôïng thöù i )
  • 81.
    * Chænh hôïp Chænhhôïp chaäp kChænh hôïp chaäp k cuûa n phaàn töû (kcuûa n phaàn töû (k ≤≤ n) laø moät nhoùm coùn) laø moät nhoùm coù thöù töï goàm k phaànthöù töï goàm k phaàn töû khaùc nhau choïntöû khaùc nhau choïn töø n phaàn töû.töø n phaàn töû.
  • 82.
    Soá chænh hôïpchaäpSoá chænh hôïp chaäp k cuûa n phaàn töûk cuûa n phaàn töû ñöôïc kyù hieäu laø:ñöôïc kyù hieäu laø: k nA )!kn( !n Ak n − =
  • 83.
    Thí duïThí duï Coùtheå thaønh laäpCoù theå thaønh laäp ñöôïc bao nhieâuñöôïc bao nhieâu concon soásoá goàm 3goàm 3 chöõ soáchöõ soá khaùc nhau töø 5 chöõkhaùc nhau töø 5 chöõ soá 1, 2, 3, 4, 5.soá 1, 2, 3, 4, 5.
  • 84.
    GiaûGiaû iiMoätMoät con soáconsoá goàm 3goàm 3 chöõchöõ soásoá khaùc nhau töø choïnkhaùc nhau töø choïn töø 5 chöõ soá 1, 2, 3, 4, 5töø 5 chöõ soá 1, 2, 3, 4, 5 chaúng haïn nhö: 153; 315;chaúng haïn nhö: 153; 315; 243; . . .243; . . . Coù theå xem nhöCoù theå xem nhö moät chænh hôïp chaäp 3moät chænh hôïp chaäp 3 cuûa 5 phaàn töû.cuûa 5 phaàn töû. Vaäy soáVaäy soá caùc con soá coù theå thaønhcaùc con soá coù theå thaønh33 55
  • 85.
    * Chænh hôïplaëp Chænh hôïp laëp chaäp kChænh hôïp laëp chaäp k cuûa n phaàn töû laø moätcuûa n phaàn töû laø moät nhoùm coù thöù töï goàm knhoùm coù thöù töï goàm k phaàn töû choïn töø nphaàn töû choïn töø n phaàn töû. Trong ñoù moãiphaàn töû. Trong ñoù moãi phaàn töû coù theå coùphaàn töû coù theå coù maët (laëp laïi) moät laàn,maët (laëp laïi) moät laàn,
  • 86.
    Vì moãi phaàntöû coùVì moãi phaàn töû coù theå coù maët nhieàu laàntheå coù maët nhieàu laàn trong moät chænh hôïptrong moät chænh hôïp laëp neân k coù theå lôùnlaëp neân k coù theå lôùn hôn n cuõng ñöôïc.hôn n cuõng ñöôïc.Soá chænh hôïp laëp chaäpSoá chænh hôïp laëp chaäp k cuûa n phaàn töû ñöôïck cuûa n phaàn töû ñöôïc kyù hieäu laøkyù hieäu laø (hoaëc )(hoaëc ) k n B k nA ~ kk n nB =
  • 87.
    ChuùChuù yùyù• Moät chænhhôïp cuõngMoät chænh hôïp cuõng chính laø moät chænh hôïpchính laø moät chænh hôïp laëp (caùc phaàn töû tronglaëp (caùc phaàn töû trong nhoùm laëp laïi toái ña 1nhoùm laëp laïi toái ña 1 laàn).laàn). • Taäp hôïp caùc chænhTaäp hôïp caùc chænh hôïp khoâng laëp laø moäthôïp khoâng laëp laø moät
  • 88.
    Thí duïThí duï 11Coùtheå thaønh laäpCoù theå thaønh laäp ñöôïc bao nhieâuñöôïc bao nhieâu con soácon soá goàm 2goàm 2 chöõ soáchöõ soá töø 4töø 4 chöõ soá 1, 2, 3, 4.chöõ soá 1, 2, 3, 4.
  • 89.
    GiaGia ûiûiVì khoâng ñoøihoûi 2 soáVì khoâng ñoøi hoûi 2 soá phaûi khaùc nhau, neânphaûi khaùc nhau, neân moãi con soá goàm 2 chöõmoãi con soá goàm 2 chöõ soá choïn töø taäp hôïpsoá choïn töø taäp hôïp goàm 4 chöõ soá: 1, 2, 3, 4,goàm 4 chöõ soá: 1, 2, 3, 4, chaúng haïn nhö: 12; 13;chaúng haïn nhö: 12; 13; 31; 24; 33; . . . coù theå xem31; 24; 33; . . . coù theå xem nhö moät chænh hôïp laëpnhö moät chænh hôïp laëp44 22 22
  • 90.
  • 91.
    Thí duïThí duï 22Xeáp3 cuoán saùch vaøo 2Xeáp 3 cuoán saùch vaøo 2 ngaên. Hoûi coù baongaên. Hoûi coù bao nhieâu caùch xeáp?nhieâu caùch xeáp? GiaûiGiaûi:: -- Xeáp caû 3 cuoánXeáp caû 3 cuoán saùch vaøo ngaên 1. Xem nhösaùch vaøo ngaên 1. Xem nhö choïn 3 soá 1 (choïn 3 soá 1 (111111).).
  • 92.
    -Xeáp cuoán 1vaøo ngaên 2,Xeáp cuoán 1 vaøo ngaên 2, xeáp cuoán 2 vaøo ngaên 1,xeáp cuoán 2 vaøo ngaên 1, xeáp cuoán 3 vaøo ngaên 2:xeáp cuoán 3 vaøo ngaên 2: ((212212)) -Khaùi quaùt:Khaùi quaùt: moãi caùchmoãi caùch xeáp 3 cuoán saùch vaøo 2xeáp 3 cuoán saùch vaøo 2 ngaên xem nhö moät chænhngaên xem nhö moät chænh hôïp laëp chaäp 3 cuûa 2.hôïp laëp chaäp 3 cuûa 2. Vaäy soá caùch xeáp laø:Vaäy soá caùch xeáp laø:22 33 33
  • 93.
    CaùchCaùch xeápxeáp ngaên 1ngaên 1Ngaên 2Ngaên 2 11  111111 22  222222 33   112112 44   112222 55   112121 66   221111 77   222211 88   221212
  • 94.
     Cuoán saùch1Cuoán saùch 1 ngaên 2ngaên 2ngaên 1ngaên 1   Cuoán saùch 2    Cuoán saùch 2211 2211 11 11 11 11 22 22 22 22 1; 112; 121; 122; 211; 212; 221;21; 112; 121; 122; 211; 212; 221;2
  • 95.
    * Hoaùn vò Hoaùnvò cuûa m phaànHoaùn vò cuûa m phaàn töû laø moät nhoùm coùtöû laø moät nhoùm coù thöù töï goàm ñuû maët mthöù töï goàm ñuû maët m phaàn töû.phaàn töû.Soá hoaùn vò cuûa mSoá hoaùn vò cuûa m phaàn töû ñöôïc kyù hieäuphaàn töû ñöôïc kyù hieäu laø Plaø Pmm !mPm =
  • 96.
    ChuùChuù yùyùCaùc hoaùn vòñeàuCaùc hoaùn vò ñeàu gioáng nhau veà thaønhgioáng nhau veà thaønh phaàn, chæ khaùc nhauphaàn, chæ khaùc nhau bôûi thöù töï saép xeápbôûi thöù töï saép xeáp cuûa caùc phaàn töûcuûa caùc phaàn töû trong nhoùm.trong nhoùm.
  • 97.
    Thí duïThí duï Xeáp3 ngöôøi vaøoXeáp 3 ngöôøi vaøo moät daõy gheá 3 choãmoät daõy gheá 3 choã ngoài. Hoûi coù baongoài. Hoûi coù bao nhieâu caùch xeáp?nhieâu caùch xeáp?
  • 98.
    GiaûiGiaûi Moãi caùch xeáp3 ngöôøiMoãi caùch xeáp 3 ngöôøi vaøo moät daõy gheá 3vaøo moät daõy gheá 3 choã ngoài ñeàu gioángchoã ngoài ñeàu gioáng nhau veà thaønh phaàn,nhau veà thaønh phaàn, chæ khaùc nhau bôûi thöùchæ khaùc nhau bôûi thöù töï saép xeáp cuûa caùctöï saép xeáp cuûa caùc phaàn töû trong nhoùm.phaàn töû trong nhoùm.
  • 99.
    Caùch xeápCaùch xeáp 11   22    33    44    55    66   
  • 100.
    ChuùChuù yùyùCoù theå duøngqui taécCoù theå duøng qui taéc nhaân thay theá chonhaân thay theá cho chænh hôïp, chænhchænh hôïp, chænh hôïp laëp, hoaùn vò.hôïp laëp, hoaùn vò.
  • 101.
    * Toå hôïpToåhôïp Toå hôïp chaäp k cuûaToå hôïp chaäp k cuûa n phaàn töû (kn phaàn töû (k ≤≤ n) laøn) laø moät nhoùm khoângmoät nhoùm khoâng phaân bieät thöù töïphaân bieät thöù töï goàm k phaàn töûgoàm k phaàn töû khaùc nhau choïn töø nkhaùc nhau choïn töø n
  • 102.
    Soá toå hôïpchaäp kSoá toå hôïp chaäp k cuûa n phaàn töû ñöôïccuûa n phaàn töû ñöôïc kyù hieäu laøkyù hieäu laø k nC )!kn(!k !n Ck n − =
  • 103.
    ChuùChuù yùyùToå hôïp vaøchænh hôïpToå hôïp vaø chænh hôïp gioáng nhau ôû choã: ñeàugioáng nhau ôû choã: ñeàu laø nhöõng nhoùm goàm klaø nhöõng nhoùm goàm k phaàn töû khaùc nhau choïnphaàn töû khaùc nhau choïn töø taäp hôïp goàm n phaàntöø taäp hôïp goàm n phaàn töû. Khaùc nhau ôû choã:töû. Khaùc nhau ôû choã: toå hôïp khoâng phaântoå hôïp khoâng phaân bieät thöù töï, chænh hôïpbieät thöù töï, chænh hôïp
  • 104.
    Thí duïThí duï 11Moätlôùp trong moätMoät lôùp trong moät hoïc kyø phaûi hoïc 5hoïc kyø phaûi hoïc 5 moân, moãi ngaøy hoïcmoân, moãi ngaøy hoïc 2 moân. Vaäy coù bao2 moân. Vaäy coù bao nhieâu caùch xeáp thôøinhieâu caùch xeáp thôøi khoùa bieåu trong moätkhoùa bieåu trong moät ngaøy?ngaøy?
  • 105.
    GiaGia ûiûiKhi xeáp thôøikhoaù bieåuKhi xeáp thôøi khoaù bieåu trong moät ngaøy neáu tatrong moät ngaøy neáu ta thay ñoåi thöù töï moânthay ñoåi thöù töï moân hoïc seõ taïo ra caùch xeáphoïc seõ taïo ra caùch xeáp khaùc. Töùc coù phaânkhaùc. Töùc coù phaân bieät thöù töï moân hoïc.bieät thöù töï moân hoïc. Vaäy moãi caùch xeáp thôøiVaäy moãi caùch xeáp thôøi khoaù bieåu trong moätkhoaù bieåu trong moät55 22
  • 106.
    CaùchCaùch xeápxeáp Caùch xeápCaùch xeáp 11 1111  22  1212  33  1313  44  1414  55  1515  66  1616  77  1717  88  1818  99  1919  1010  2020 
  • 107.
    Thí duïThí duï 22Coù5 ñoäi boùng thiCoù 5 ñoäi boùng thi ñaáu vôùi nhau theoñaáu vôùi nhau theo caùch: 2 ñoäi baát kyøcaùch: 2 ñoäi baát kyø trong 5 ñoäi boùngtrong 5 ñoäi boùng naøy phaûi thi ñaáunaøy phaûi thi ñaáu vôùi nhau moät traän.vôùi nhau moät traän. Hoûi phaûi toå chöùcHoûi phaûi toå chöùc
  • 108.
    GiaGia ûiûiMoät traän giöõahai ñoäiMoät traän giöõa hai ñoäi boùng thì khoâng caànboùng thì khoâng caàn phaân bieät thöù töï cuûaphaân bieät thöù töï cuûa hai ñoäi boùng ñoù. Vì vaäyhai ñoäi boùng ñoù. Vì vaäy moät traän ñaáu giöõa 2moät traän ñaáu giöõa 2 ñoäi choïn trong soá 5 ñoäiñoäi choïn trong soá 5 ñoäi boùng laø moät toå hôïpboùng laø moät toå hôïp chaäp 2 cuûa 5. Vaäy soáchaäp 2 cuûa 5. Vaäy soá55 22
  • 109.
    SoáSoá tttt SoáSoá tttt 11 ABAB 66BDBD 22 ACAC 77 BEBE 33 ADAD 88 CDCD 44 AEAE 99 CECE 55 BCBC 1010 DEDE
  • 110.
    •Chuù yù: • ÑeåtínhÑeå tính • coù theå duøng caùccoù theå duøng caùc haøm:haøm: • COMBIN(n,k); FACT(m);COMBIN(n,k); FACT(m); • PERMUT(n,k); POWER(n,kPERMUT(n,k); POWER(n,k)) • trong Exceltrong Excel (xem phuï(xem phuï luïc 1)luïc 1) k n k nm k n B;A;P;C
  • 111.
    4- Ñònh nghóathoáng4- Ñònh nghóa thoáng keâ cuûakeâ cuûa xaùc suaátxaùc suaát Xeùt pheùp thöûXeùt pheùp thöû ττ vaøvaø A laø moät bieán coá.A laø moät bieán coá. Giaû söû ta coù theåGiaû söû ta coù theå thöïc hieän laëp laïithöïc hieän laëp laïi pheùp thöûpheùp thöû ττ voâ haïnvoâ haïn
  • 112.
    Khi thöïc hieänpheùpKhi thöïc hieän pheùp thöûthöû ττ n laàn ta thaáyn laàn ta thaáy coù k laàn bieán coácoù k laàn bieán coá A xaûy ra, ta goïi tyûA xaûy ra, ta goïi tyû soásoá laø taàn suaát cuûalaø taàn suaát cuûa bieán coá A trong nbieán coá A trong n kk nn
  • 113.
    fn(A) = Khi ntaêng voâ haïnKhi n taêng voâ haïn taàn suaát ftaàn suaát fnn(A) caøng(A) caøng gaàn moät soá khoânggaàn moät soá khoâng ñoåi p, khi ñoù:ñoåi p, khi ñoù: P(A) = lim fn(A) = p n→∞ n k
  • 114.
    Trong thöïc teá,khi nTrong thöïc teá, khi n ñuû lôùn, ta xaáp xæñuû lôùn, ta xaáp xæ P(A)P(A) ≈≈ ffnn(A)(A)Thí duï: 1-1- Tính xaùc suaát ñeåTính xaùc suaát ñeå moät maùy saûn xuaátmoät maùy saûn xuaát ra pheá phaåmra pheá phaåm2-2- Tính xaùc suaát ñeåTính xaùc suaát ñeå xe oâ toâ bò tai naïn.xe oâ toâ bò tai naïn.
  • 115.
    IV- Caùc coângthöùcIV- Caùc coâng thöùc tính xaùc suaáttính xaùc suaát  Neáu A vaø B laø haiNeáu A vaø B laø hai bieán coá xung khaéc thì:bieán coá xung khaéc thì: P(AP(A ∪∪ B) = P(A) +B) = P(A) + P(B)P(B) 1-1- Coâng thöùc coäng xaùcCoâng thöùc coäng xaùc suaátsuaát::
  • 116.
    Toång quaùt:    NeáuANeáu A11, A, A22, . . . , A, . . . , Ann laølaø n bieán coá xung khaécn bieán coá xung khaéc töøng ñoâi, thì:töøng ñoâi, thì: P(AP(A11 ∪∪ AA22 ∪∪ . . .. . . ∪∪ AAnn) =) = P(AP(A11) +) +
  • 117.
    Heä quaû:Heä quaû:Neáu A vaøNeáu A vaø laø hai bieán coá ñoái laäplaø hai bieán coá ñoái laäp nhau thì:nhau thì: A P(A) = 1P(A) = 1 −− P( )P( )A
  • 118.
     Neáu Avaø B laø haiNeáu A vaø B laø hai bieán coá khoâng xungbieán coá khoâng xung khaéc thì:khaéc thì:P(AP(A ∪∪ B) = P(A) + P(B)B) = P(A) + P(B) −− P(AB)P(AB) +−−− ++=∪∪ )AA(P)AA(P)AA(P )A(P)A(P)A(P)AAA(P 323121 321321 )AAA(P 321+ Tröôøng hôïp n = 3:Tröôøng hôïp n = 3: NeáuNeáu AA11, A, A22, A, A33 laø caùc b/coálaø caùc b/coá khoâng xung khaéc, thì:khoâng xung khaéc, thì:
  • 119.
    Thí duï 1Thíduï 1:: Moät hoäp coù 5 saûn phaåm (trong ñoù coù 3 saûn phaåm loaïi I vaø 2 saûn phaåm loaïi II. Laáy ngaãu nhieân töø hoäp ra 2 saûn phaåm. Tìm xaùc suaát ñeå coù
  • 120.
    GiaûiGiaûi:: Goïi AGoïiA00 laø b/claø b/c “khoâng coù saûn phaåm“khoâng coù saûn phaåm loaïi I naøo trong 2 saûnloaïi I naøo trong 2 saûn phaåm laáy ra”; Aphaåm laáy ra”; A11 laø b/claø b/c “coù 1 saûn phaåm loaïi I“coù 1 saûn phaåm loaïi I trong 2 saûn phaåm laáytrong 2 saûn phaåm laáy ra”; A laø b/c”coù khoângra”; A laø b/c”coù khoâng quaù 1 saûn phaåm loaïi Iquaù 1 saûn phaåm loaïi I trong 2 saûn phaåm laáytrong 2 saûn phaåm laáy A = AA = A00 ∪∪ AA11 AA00, A, A11 xung khaéc.xung khaéc.
  • 121.
    P(A) = P(AP(A)= P(A00 ∪∪ AA11) = P(A) = P(A00) +) + P(AP(A11)) P(AP(A00) = = = 0,1) = = = 0,1 CC CC 2 22 22 55 11 1010 P(AP(A11) = = =) = = = 0,60,6 CC CC CC 55 33 11 11 22 22 1010 66 ⇒⇒ P(A) = 0,1 + 0,6 =P(A) = 0,1 + 0,6 = 0,70,7
  • 122.
    1-1- Xaùc suaáùtXaùcsuaáùt coù ñieàu kieäncoù ñieàu kieän 2- Coâng thöùc nhaân2- Coâng thöùc nhaân xaùc suaátxaùc suaát a-a- ÑònhÑònh nghóanghóa::Xaùc suaát cuûa bieán coáXaùc suaát cuûa bieán coá A ñöôïc tính vôùi ñieàuA ñöôïc tính vôùi ñieàu kieän bieán coá B ñaõkieän bieán coá B ñaõ xaûy ra goïi laø xaùcxaûy ra goïi laø xaùc
  • 123.
    b-b- Coâng thöùctínhCoâng thöùc tính:: Ñeå tính xaùc suaát coùÑeå tính xaùc suaát coù ñieàu kieän, tuøy theoñieàu kieän, tuøy theo ñieàu kieän cuï theå cuûañieàu kieän cuï theå cuûa baøi toaùn ta coù theåbaøi toaùn ta coù theå duøng: ñònh nghóa coåduøng: ñònh nghóa coå ñieån, coâng thöùc Bayes,ñieån, coâng thöùc Bayes, hoaëc aùp duïng coânghoaëc aùp duïng coâng
  • 124.
    P(A/B)P(A/B) == c- Thí duï:c-Thí duï: Moät lôùp coùMoät lôùp coù 50 s/v (20 nöõ vaø 30 nam,50 s/v (20 nöõ vaø 30 nam, trong ñoù coù 5 nöõ gioûitrong ñoù coù 5 nöõ gioûi toaùn). Gaëp ng.n moät s/vtoaùn). Gaëp ng.n moät s/v cuûa lôùp. Tìm xaùc suaátcuûa lôùp. Tìm xaùc suaát P(AB)P(AB) P(B)P(B)
  • 125.
    GiaûiGiaûi:: Goïi Alaø bieánGoïi A laø bieán coá “gaëp ñöôïc s/v gioûicoá “gaëp ñöôïc s/v gioûi toaùn”; B laø bieán coátoaùn”; B laø bieán coá “gaëp ñöôïc s/v nöõ”. Ta“gaëp ñöôïc s/v nöõ”. Ta caàn tìm P(A/B).caàn tìm P(A/B). P(A/B)P(A/B) == P(AB)P(AB) P(BP(B )) == 5/5/ 505020/520/5 00 == 0,250,25
  • 126.
    Hai bieán coáA, B ñöôïcHai bieán coá A, B ñöôïc goïi laø ñoäc laäp vôùigoïi laø ñoäc laäp vôùi nhau neáu:nhau neáu: P(A/B) = P(A)P(A/B) = P(A) HoaëcHoaëc P(B/A) = P(B)P(B/A) = P(B)Vieäc xaûy ra hay khoângVieäc xaûy ra hay khoâng xaûy ra cuûa b/c naøyxaûy ra cuûa b/c naøy khoâng aûnh höôûng ñeánkhoâng aûnh höôûng ñeán
  • 127.
    Hai bieán coáA, BHai bieán coá A, B ñöôïc goïi laø ñoäcñöôïc goïi laø ñoäc laäp vôùi nhau khilaäp vôùi nhau khi vaø chæ khi:vaø chæ khi: P(AB) =P(AB) = P(A).P(B)P(A).P(B)
  • 128.
    Neáu A, Bñoäc laäpNeáu A, B ñoäc laäp thì:thì: A, B; A, B vaø A, BA, B; A, B vaø A, B cuõng ñoäc laäp.cuõng ñoäc laäp.
  • 129.
    Caùc b/c ACaùcb/c A11, A, A22, . . . A, . . . Ann ñöôïc goïi laø ñoäc laäpñöôïc goïi laø ñoäc laäp toaøn phaàn neáu moãitoaøn phaàn neáu moãi b/c ñoäc laäp vôùi moätb/c ñoäc laäp vôùi moät toå hôïp baát kyø trongtoå hôïp baát kyø trong caùc bieán coá coøn laïi.caùc bieán coá coøn laïi.
  • 130.
    Neáu A, Blaø hai b/cNeáu A, B laø hai b/c baát kyø thì:baát kyø thì: P(AB) =P(AB) = P(A).P(B/A)P(A).P(B/A) == P(B).P(A/B)P(B).P(A/B) 2-2- Ñònh lyù:Ñònh lyù:
  • 131.
    Toång quaùtToång quaùt:: P(AP(A11AA22. . . A. . . Ann) =) = P(AP(A11)P(A)P(A22 /A/A11). . .). . . P(AP(Ann/A/A11AA22. . . A. . . An-1n-1)) Neáu ANeáu A11, A, A22, . . . A, . . . Ann laølaø caùc b/c baát kyø, thì:caùc b/c baát kyø, thì:
  • 132.
    (xem thí duïtrang 36)(xem thí duï trang 36)
  • 133.
    Neáu A, Blaø hai b/coáNeáu A, B laø hai b/coá ñoäc laäp, thì:ñoäc laäp, thì: Heä quaû:Heä quaû: P(AB) =P(AB) = P(A)P(B)P(A)P(B)
  • 134.
    P(AP(A11AA22 . ... . . AAnn)=P(A)=P(A11)P(A)P(A22)). . .. . . P(AP(Ann)) Toång quaùtToång quaùt:: NeáuNeáu AA11,, AA22 , . . . , A, . . . , Ann laø caùc b/c ñoäc laäplaø caùc b/c ñoäc laäp toaøn phaàn, thì:toaøn phaàn, thì:
  • 135.
    Chia ngaãu nhieân9 hoäp söõa (trong ñoù coù 3 hoäp keùm phaåm chaát) thaønh 3 phaàn, moãi phaàn 3 hoäp. Tính xaùc suaát Thí duïThí duï::
  • 136.
    GiaûiGiaûi:: Goïi AGoïiAii (i = 1, 2) laø(i = 1, 2) laø bieán coá phaàn thöù i coùbieán coá phaàn thöù i coù 1 hoäp söõa keùm phaåm1 hoäp söõa keùm phaåm chaát.chaát.A laø bieán coá moãiA laø bieán coá moãi phaàn coù 1 hoäp keùmphaàn coù 1 hoäp keùm phaåm chaát.phaåm chaát. (A2 phuï thuoäc A1 ). AÙp duïng coâng thöùc nhaân A = AA = A11AA22
  • 137.
    P(A) = P(AP(A)= P(A11)P(A)P(A22/A/A11)) 28 9 C C.C . C C.C 3 6 2 4 1 2 3 9 2 6 1 3 ==
  • 138.
    3- Coâng thöùcxaùc suaát3- Coâng thöùc xaùc suaát ñaày ñuûñaày ñuû • Cho khoâng gian maãu SCho khoâng gian maãu S vaø Avaø A11, A, A22, . . . , A, . . . , Ann , B laø, B laø caùc bieán coá.caùc bieán coá. • Caùc bieán coá ACaùc bieán coá A11,, AA22, . . . , A, . . . , Ann laø heä bieánlaø heä bieán coá ñaày ñuû neáu chuùngcoá ñaày ñuû neáu chuùng thoûa maõn 2 ñieàu kieänthoûa maõn 2 ñieàu kieän
  • 139.
    (1) A1 ∪A2 . . . ∪ An = Ω (2) Ai ∩ Aj = ∅ (∀i ≠ j) i, j ∈{1, 2, . . . , n}• Khi ñoù ta coù:Khi ñoù ta coù:
  • 140.
    P(B) =P(B) = (A(Aii)P(B/A)P(B/Aii)) ∑= n 1i P Caùcxaùc suaát P(ACaùc xaùc suaát P(A11);); P(AP(A22); . . . , P(A); . . . , P(Ann) thöôøng) thöôøng ñöôïc goïi laø caùc xaùcñöôïc goïi laø caùc xaùc suaát tieân nghieäm vaøsuaát tieân nghieäm vaø coâng thöùc treân ñöôïccoâng thöùc treân ñöôïc goïi laøgoïi laø coâng thöùc xaùccoâng thöùc xaùc
  • 141.
    Thí duïThí duï::Coù 3 kieänCoù 3 kieän haøng. Moãi kieän coù 5haøng. Moãi kieän coù 5 saûn phaåm, soá saûnsaûn phaåm, soá saûn phaåm loaïi A coù trongphaåm loaïi A coù trong kieän 1, kieän 2, kieän 3kieän 1, kieän 2, kieän 3 töông öùng laø: 4, 3, 2.töông öùng laø: 4, 3, 2. Choïn ngaãu nhieân moätChoïn ngaãu nhieân moät kieän roài töø kieän ñaõkieän roài töø kieän ñaõ choïn laáy ngaãu nhieân rachoïn laáy ngaãu nhieân ra
  • 142.
    Giaûi:Giaûi: Goïi B laøbieán coá laáyGoïi B laø bieán coá laáy ñöôïc saûn phaåm loaïi A.ñöôïc saûn phaåm loaïi A. AA11, A, A22, A, A33 töông öùng laøtöông öùng laø caùc bieán coá choïn ñöôïccaùc bieán coá choïn ñöôïc kieän 1, 2, 3.kieän 1, 2, 3. AA11, A, A22, A, A33 laø moät heä bieánlaø moät heä bieán coá ñaày ñuû.coá ñaày ñuû.
  • 143.
    KieänKieän 11 KieänKieän 22 KieänKieän 33             
  • 144.
  • 145.
    3 1 )A(P)A(P)A(P 321 === ∑= = 3 1i ii )A/B(P)A(P)B(P P(B/AP(B/A11)= = 0,8) = = 0,844 55 P(B/AP(B/A22) = =) = = 0,60,6 55 33 P(B/AP(B/A33) = =) = = 55 22
  • 146.
    P(B) = (0,8+ 0,6 + 0,4)P(B) = (0,8 + 0,6 + 0,4) = 0,6= 0,6 11 33
  • 147.
    4- Coâng thöùcBayes4- Coâng thöùc Bayes Vôùi caùc giaû thieát nhöVôùi caùc giaû thieát nhö phaàn coâng thöùc xaùcphaàn coâng thöùc xaùc suaát ñaày ñuû vaø tasuaát ñaày ñuû vaø ta theâm ñieàu kieän laøtheâm ñieàu kieän laø pheùp thöû ñöôïc thöïcpheùp thöû ñöôïc thöïc hieän vaø bieán coá B ñaõhieän vaø bieán coá B ñaõ xaûy ra. Khi ñoù:xaûy ra. Khi ñoù:
  • 148.
    P(AP(Aii/B) =/B) = (i = 1, 2, .( i = 1, 2, . . . , n). . , n) )B(P )A/B(P)A(P ii
  • 149.
    Caùc xaùc suaátP(ACaùc xaùc suaát P(Aii/B)/B) ñöôïc xaùc ñònh sau khiñöôïc xaùc ñònh sau khi ñaõ bieát keát quaû cuûañaõ bieát keát quaû cuûa pheùp thöû laø B ñaõ xaûypheùp thöû laø B ñaõ xaûy ra neân thöôøng ñöôïc goïira neân thöôøng ñöôïc goïi laø caùclaø caùc xaùc suaát haäuxaùc suaát haäu nghieämnghieäm.. Coâng thöùc Bayes xaùcCoâng thöùc Bayes xaùc ñònh laïi caùcñònh laïi caùc xaùc suaátxaùc suaát tieân nghieämtieân nghieäm P(AP(Aii)) khikhi
  • 150.
    Thí duïThí duï::Coù 3 kieänCoù 3 kieän haøng. Moãi kieän coù 5haøng. Moãi kieän coù 5 saûn phaåm, soá saûnsaûn phaåm, soá saûn phaåm loaïi A coù trongphaåm loaïi A coù trong kieän 1, kieän 2, kieän 3kieän 1, kieän 2, kieän 3 töông öùng laø: 4, 3, 2.töông öùng laø: 4, 3, 2. Choïn ngaãu nhieân moätChoïn ngaãu nhieân moät kieän roài töø kieän ñaõkieän roài töø kieän ñaõ choïn laáy ngaãu nhieân rachoïn laáy ngaãu nhieân ra
  • 151.
    Giaûi:Giaûi: Goïi B laøbieán coá laáyGoïi B laø bieán coá laáy ñöôïc saûn phaåm loaïi A.ñöôïc saûn phaåm loaïi A. AA11, A, A22, A, A33 töông öùng laøtöông öùng laø caùc bieán coá choïn ñöôïccaùc bieán coá choïn ñöôïc kieän 1, 2, 3.kieän 1, 2, 3. AA11, A, A22, A, A33 laø moät heä bieánlaø moät heä bieán coá ñaày ñuû.coá ñaày ñuû.
  • 152.
    Vì bieán coáB ñaõ xaûy ra, aùp duïng coâng thöùc Bayes ta coù: P(AP(A33/B) =/B) = == 11 33 0,40,4 0,60,6 99 22
  • 153.
    TOÙM TAÉT CHÖÔNG1TOÙM TAÉT CHÖÔNG 1 PheùpPheùp thöûthöû BieánBieán coácoá XaùcXaùc suaátsuaát cuûacuûa bieánbieán coácoá •• ÑN coå ñieånÑN coå ñieån •• ÑN thoángÑN thoáng keâkeâ •• Caùc coângCaùc coâng thöùcthöùc cô baûncô baûn •• Caùc loaïi b/cCaùc loaïi b/c •• Moái quan heäMoái quan heä Ñieàu kieänÑieàu kieän aùp duïngaùp duïng
  • 154.
    Baøi taäp chuông1Baøi taäp chuông 1 1.10; 1.15;1.10; 1.15; 1.16;1.16; 1.35; 1.36;1.35; 1.36; 1.39;1.39; 1.43; 1.48;1.43; 1.48; 1.49;1.49;
  • 155.