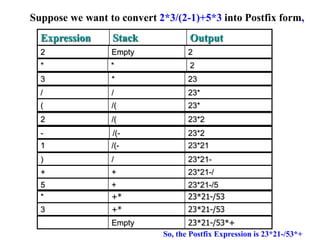
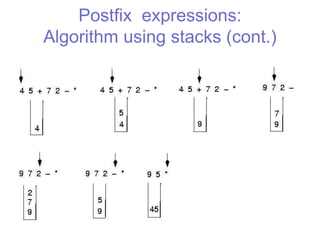
This document discusses stacks and their applications. It begins with an introduction to stacks, describing them as data structures that follow the last-in, first-out (LIFO) principle. It then outlines stack operations like push, pop, top, and describes how stacks can be implemented using arrays or linked lists. Several applications of stacks are mentioned, including parenthesis matching, expression evaluation in postfix notation, handling function calls and returns, and undo sequences. Examples are provided to illustrate postfix notation, converting infix to postfix expressions, and evaluating postfix expressions using a stack.

1. Chapter 6
Stacks
Dr. Muhammad Hanif Durad
Department of Computer and Information Sciences
Pakistan Institute Engineering and Applied Sciences
hanif@pieas.edu.pk
Some slides have bee adapted with thanks from some other lectures
available on Internet. It made my life easier, as life is always
miserable at PIEAS (Sir Muhammad Yusaf Kakakhil )

2. Dr. Hanif Durad 2
Lecture Outline
 Introduction
 Stack
 Stack operations
 Implementation of Stacks
 Arrays
 Linked lists
 Applications of Stack

3. Introduction
 Stack
 The element deleted from the set is the one
most recently inserted
 Last-in, First-out (LIFO)
D:DSAL5165 Advanced Algorithm and Programming Languageunit09.ppt

4. Introduction
 Stack operations
 PUSH: Insert
 POP: Delete
 TOP: return the key value of the most recently
inserted element
 STACK-EMPTY: check if the stack is empty
 STACK-FULL: check if the stack is full

5. An Example of Stack
2
8
1
7
2
7
2
1
7
2
1
7
2
8
1
7
2
8
1
7
2
top
top
top
top
top
top
Push(8) Push(2)
pop(2)
pop(8)pop(1)
D:Data StructuresICS202Lecture10.ppt

6. Implementation of Stacks
 Any list implementation could be used to
implement a stack
 Arrays (static: the size of stack is given initially)
 Linked lists (dynamic: never become full)
 We will explore implementations based on array
and linked list
 Let’s see how to use an array to implement a
stack first

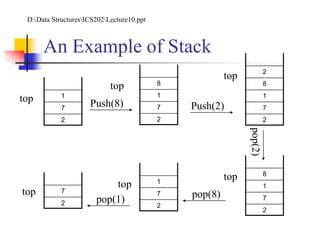
7. Represent Stack by Array
 A stack of at most n elements can be implemented by an array
S[1..n]
 top[S]: a pointer to the most recently inserted element
 A stack consists of elements S[1..top[S]]
 S[1]: the element at the bottom of the stack
 S[top[S]]: the element at the top

8. Stack Operations
How to implement
TOP(S), STACK-FULL(S) ?
O(1)

9. Illustration of PUSH
15 6 2 9S
top[S]=4
PUSH(S, 17)
15 6 2 9S
top[S]=4
top[S]=5
top[S]  top[S] + 1 (top[S] = 5)
S[top[S]]  x (S[5] = 17)
17

10. Illustration of POP
15 6 2 9 17 3S
top[S]=6
POP(S)
15 6 2 9 17 3S
top[S]=6
top[S]=5
top[S]  top[S] - 1 (top[S] = 5)
return S[top[S]+1] (return S[6])
3

11. 11
 Nodes (data, pointer) connected in a chain by links
 the head or the tail of the list could serve as the top of
the stack
Linked List Implementation
D:Data StructuresHanif_SearchQueuesad5.ppt

12. Applications of Stack
Dr. Hanif Durad 12

13. Applications of Stack
 Direct applications
 Parenthesis matching
 Polish postfix and prefix notations
 Expression evaluations
 Undo sequence in a text editor
 Handling function calls and return
 Handling recursion
 Indirect applications
 Auxiliary data structure for algorithms
 Component of other data structures
+++ many more

14. Parenthesis Matching (1/2)
 To check that every right brace, bracket, and
parentheses must correspond to its left
counterpart
 e.g. [( )] is legal, but [( ] ) is illegal
Dr. Hanif Durad 14
D:Data StructuresHanif_SearchStacks stack-queue.ppt,P-18/44

15. Parenthesis Matching (2/2)
 Algorithm
(1) Make an empty stack.
(2) Read characters until end of file
i. If the character is an opening symbol, push it onto the stack
ii. If it is a closing symbol, then if the stack is empty, report an
error
iii. Otherwise, pop the stack. If the symbol popped is not the
corresponding opening symbol, then report an error
(3) At end of file, if the stack is not empty, report an err
Dr. Hanif Durad 15

16. Parenthesis Matching Example
Dr. Hanif Durad 16
D:Data StructuresHanif_SearchStacks
Example: On board. DS1, P-185

17. 17
RPN or Postfix Notation
 Most compilers convert an expression in infix
notation to postfix
 the operators are written after the operands
 So a * b + c becomes a b * c +
 Advantage:
 expressions can be written without parentheses
chapter07.ppt

18. 18
Postfix and Prefix Examples
INFIX RPN (POSTFIX) PREFIX
A + B
A * B + C
A * (B + C)
A - (B - (C - D))
A - B - C - D
* A + B C
+ * A B C
-A-B-C D
---A B C D
+ A B
Prefix : Operators come before
the operands
A B +
A B * C +
A B C + *
A B C D---
A B-C-D-

19. Algorithm for Infix to Postfix
1) Examine the next element in the input.
2) If it is operand, output it.
3) If it is opening parenthesis, push it on stack.
4) If it is an operator, then
i) If stack is empty, push operator on stack.
ii) If the top of stack is opening parenthesis, push operator on stack
iii) If it has higher priority than the top of stack, push operator on
stack.
iv) Else pop the operator from the stack and output it, repeat step 4
5) If it is a closing parenthesis, pop operators from stack and output
them until an opening parenthesis is encountered. pop and discard
the opening parenthesis.
6) If there is more input go to step 1
7) If there is no more input, pop the remaining operators to output.
Lecture 10,11 Stacks.pptx

20. Suppose we want to convert 2*3/(2-1)+5*3 into Postfix form,
So, the Postfix Expression is 23*21-/53*+
2 Empty 2
* * 2
3 * 23
/ / 23*
( /( 23*
2 /( 23*2
- /(- 23*2
1 /(- 23*21
) / 23*21-
+ + 23*21-/
5 + 23*21-/5
3 +* 23*21-/53
Expression Stack Output
* +* 23*21-/53
Empty 23*21-/53*+

21. Evaluation a postfix expression
• Each operator in a postfix string refers to the
previous two operands in the string.
• Suppose that each time we read an operand we
push it into a stack. When we reach an operator,
its operands will then be top two elements on the
stack
• We can then pop these two elements, perform the
indicated operation on them, and push the result
on the stack.
• So that it will be available for use as an operand of
the next operator.

22. Evaluating Postfix Notation
• Use a stack to evaluate an expression
in postfix notation.
• The postfix expression to be evaluated
is scanned from left to right.
• Variables or constants are pushed onto
the stack.
• When an operator is encountered, the
indicated action is performed using the
top elements of the stack, and the result
replaces the operands on the stack.

23. Evaluating a postfix expression
• Initialise an empty stack
• While token remain in the input stream
–Read next token
–If token is a number, push it into the stack
–Else, if token is an operator, pop top two
tokens off the stack,apply the operator, and
push the answer back into the stack
• Pop the answer off the stack.

24. Example: postfix expressions
(cont.)

25. Postfix expressions:
Algorithm using stacks (cont.)

26. Function calls
 Programming languages use stacks to keep track of
function calls
 When a function call occurs
 Push CPU registers and program counter on to stack
(“activation record” or “stack frame”)
 Upon return, restore registers and program counter from
top stack frame and pop
Dr. Hanif Durad 26
D:Data StructuresCPT S 223adt.ppt, P-47/52