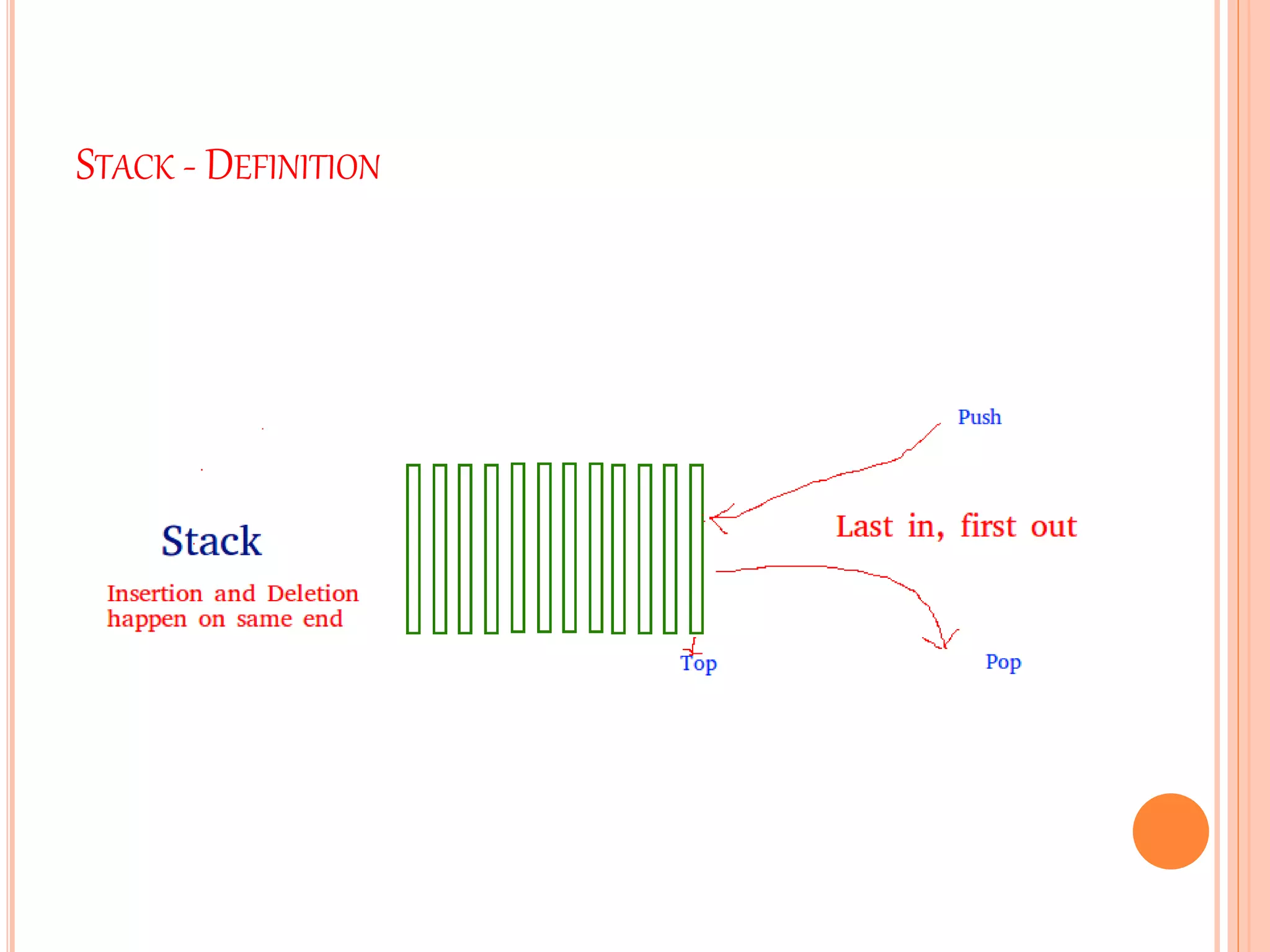
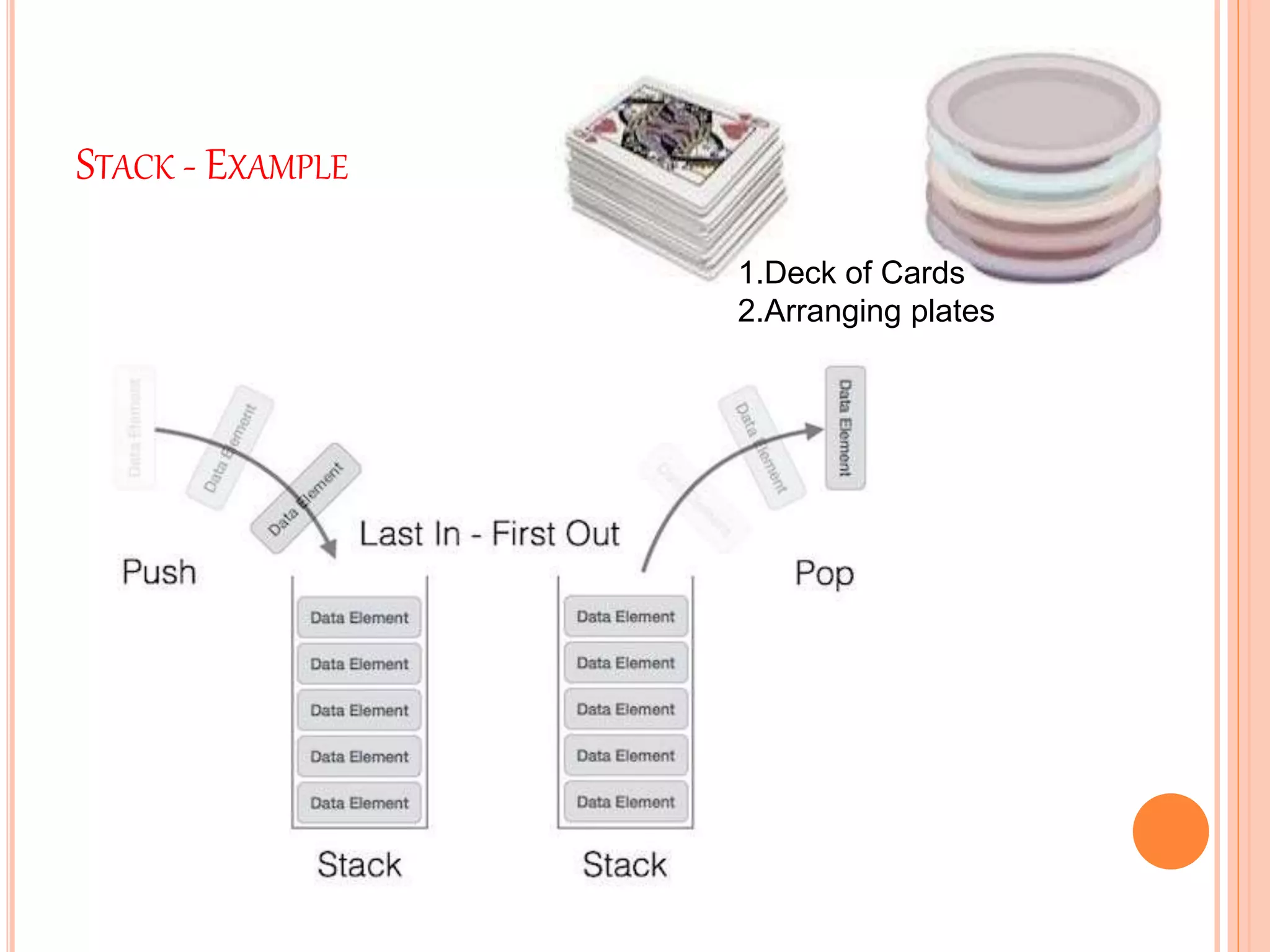
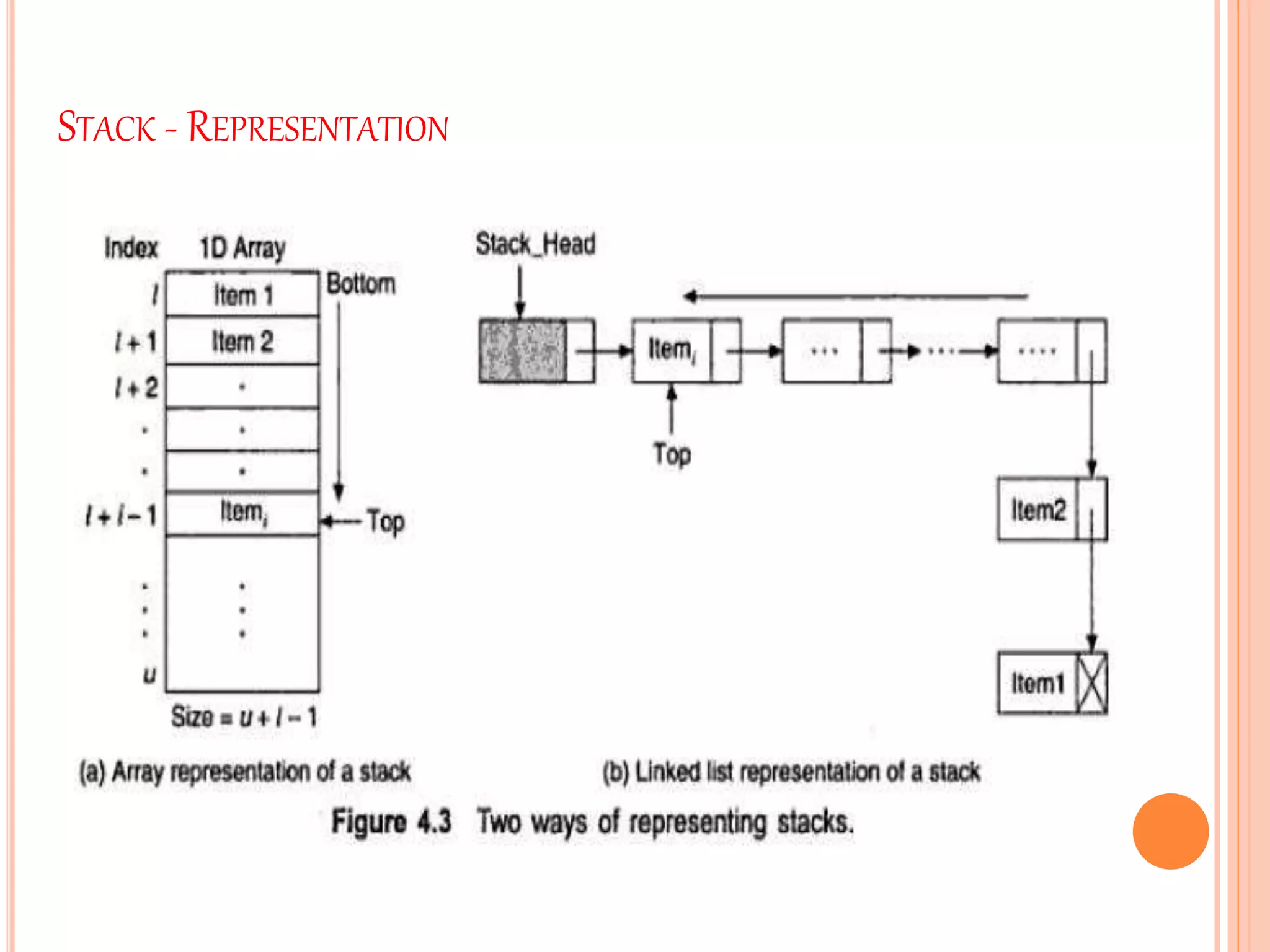
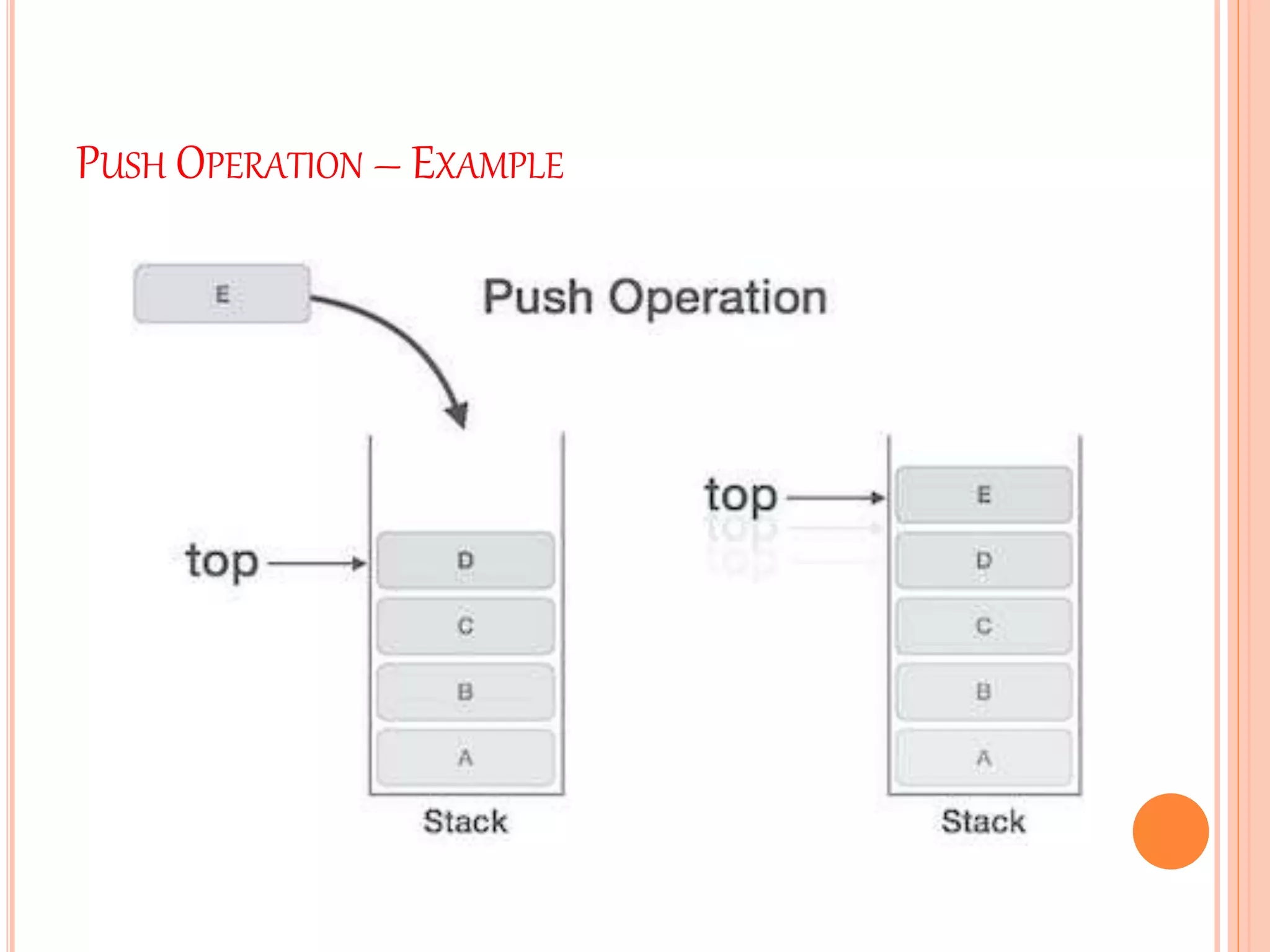
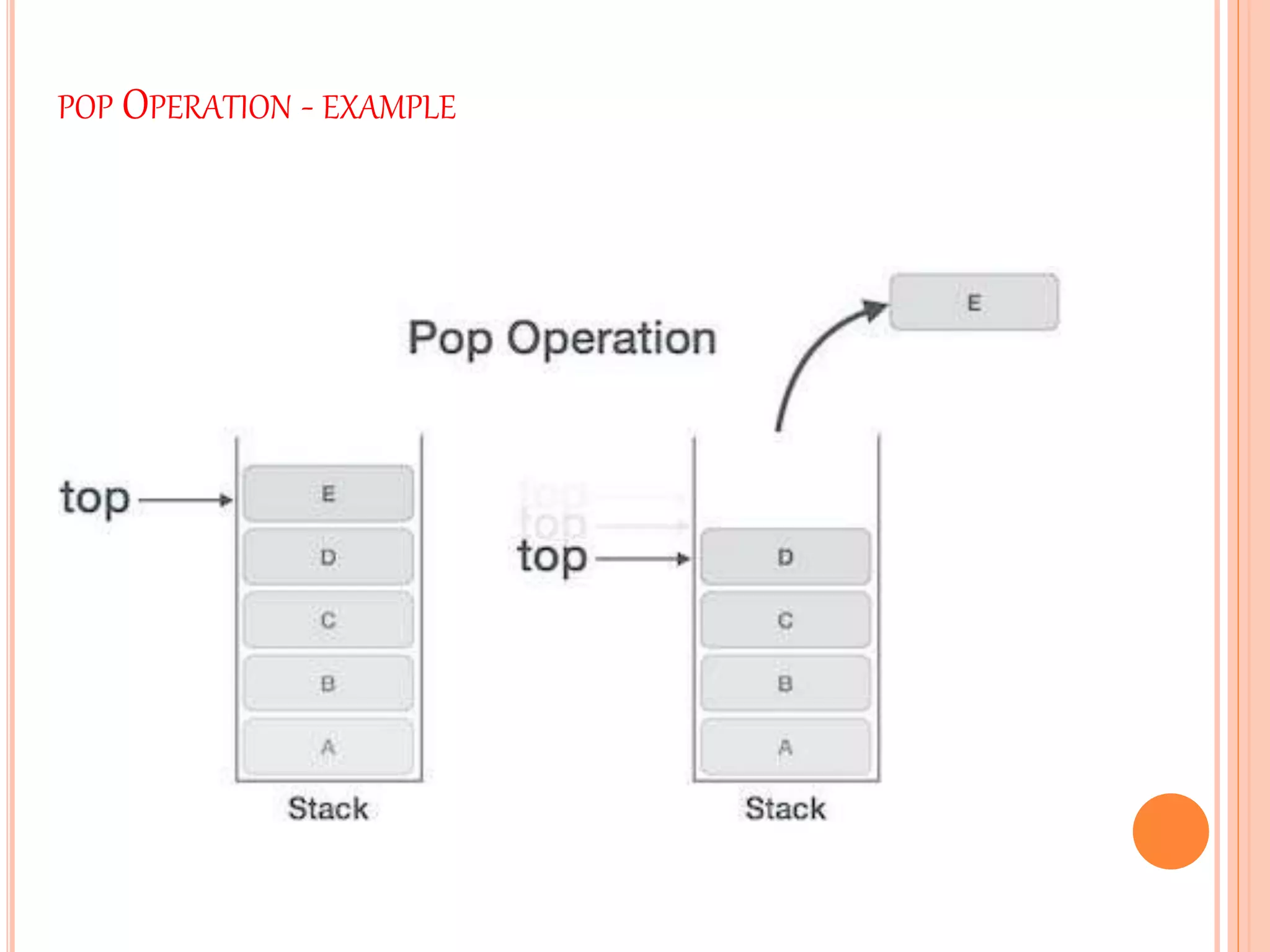
This document discusses stacks and their operations. It defines a stack as a linear data structure that follows LIFO (last-in, first-out) ordering. Elements are inserted and removed from one end only, called pushing and popping. Stacks have common real-world examples like decks of cards. They can be represented using arrays or linked lists. The core stack operations are push, which adds an element, and pop, which removes the top element. Additional operations check the stack status, like if it is full or empty. Pseudocode is provided for implementing push, pop, and status checks in both array-based and linked list-based stacks.

1. STACK AND ITS OPERATIONS
Mrs.G.Chandraprabha,M.Sc.,M.Phil.,
Assistant Professor,
Department of Information Technology,
V.V.Vanniaperumal College for Women,
Virudhunagar.

2. STACK - INTRODUCTION
 A stack is an Abstract Data Type (ADT), commonly used in
most programming languages.
 It is named stack as it behaves like a real-world stack, for
example – a deck of cards or a pile of plates, etc.
 A real-world stack allows operations at one end only. For
example, we can place or remove a card or plate from the
top of the stack only.
 Likewise, Stack ADT allows all data operations at one end
only. At any given time, we can only access the top element
of a stack.

3. STACK - DEFINITION
 Stack is an example of Linear data structure which follows the
LIFO order.
 LIFO stands for Last-in-first-out.
 Here, the element which is placed (inserted or added) at end
is accessed at first.
 Both insertion and deletion can be done in one end whic
 In stack terminology, insertion operation is
called PUSH operation and removal operation is
called POP operation.

4. STACK - DEFINITION

5. STACK - EXAMPLE
1.Deck of Cards
2.Arranging plates

6. STACK - REPRESENTATION
 A stack may be represented in the memory in various ways.
There are two main ways: using a one-dimensional array and a
single linked list.
 Array Representation of Stacks: First we have to allocate a
memory block of sufficient size to accommodate the full capacity
of the stack. Then, starting from the first location of the memory
block, the items of the stack can be stored in a sequential fashio
 In Figure, Itemi denotes the ith item in the stack; l and u denote
the index range of the array in use; usually the values of these
indices are 1 and SIZE respectively.

7. STACK - REPRESENTATION
 TOP is a pointer to point the position of the array up to which it
is filled with the items of the stack. With this representation,
the following two ways can be stated:
 EMPTY: TOP < l
FULL: TOP ≥ u
 Linked List Representation of Stacks: Although array
representation of stacks is very easy and convenient but it
allows the representation of only fixed sized stacks. In several
applications, the size of the stack may vary during program
execution.

8. STACK - REPRESENTATION
 An obvious solution to this problem is to represent a stack using
a linked list.
 A single linked list structure is sufficient to represent any stack.
 Here, the DATA field is for the ITEM, and the LINK field is, as
usual, to point to the next' item.
 In the linked list representation, the first node on the list is the
current item that is the item at the top of the stack and the last
node is the node containing the bottom-most item.
 Thus, a PUSH operation will add a new node in the front and a
POP operation will remove a node from the front of the list.

9. STACK - REPRESENTATION

10. OPERATIONS ON STACK
 A stack is used for the following two primary operations,
 push() − Pushing (storing) an element on the stack.
 pop() − Removing (accessing) an element from the
stack.
 When data is PUSHed onto stack.
 To use a stack efficiently, we need to check the status of stack
as well. For the same purpose, the following functionality is
added to stacks −
 peek() − get the top data element of the stack, without
removing it.
 isFull() − check if stack is full.
 isEmpty() − check if stack is empty.

11. PUSH OPERATION
 The process of putting a new data element onto
stack is known as a Push Operation. Push
operation involves a series of steps −
 Step 1 − Checks if the stack is full.
 Step 2 − If the stack is full, produces an error and
exit.
 Step 3 − If the stack is not full, increments top to
point next empty space.
 Step 4 − Adds data element to the stack location,
where top is pointing.
 Step 5 − Returns success.

12. PUSH OPERATION – ARRAY ALGORITHM

13. PUSH OPERATION – EXAMPLE

14. POP OPERATION
 Removing an element from the stack, is known as a Pop
Operation. In an array implementation of pop() operation, the
data element is not actually removed, instead top is
decremented to a lower position in the stack to point to the
next value. But in linked-list implementation, pop() actually
removes data element and deallocates memory space.
 A Pop operation may involve the following steps −
 Step 1 − Checks if the stack is empty.
 Step 2 − If the stack is empty, produces an error and exit.
 Step 3 − If the stack is not empty, accesses the data element
at which top is pointing.
 Step 4 − Decreases the value of top by 1.
 Step 5 − Returns success.

15. POP OPERATION – ARRAY ALGORITHM

16. POP OPERATION - EXAMPLE

17. STATUS_ARRAY OPERATION - ALGORITHM
 Status_Array , we test the various states of a stack such as
whether it is full or empty, how many items are right now in
it, and read the current element at the top without
removing it, etc.

18. PUSH OPERATION - LINKED LIST ALGORITHM

19. POP OPERATION - LINKED LIST ALGORITHM

20. STATUS OPERATION - LINKED LIST ALGORITHM

21. THANKYOU